工程优化方法综述

一、优化建模

1 概 述

建立数学模型是优化设计中的一个重要的组成部分。优化结构是否可用，主要取决于所建立的数学模型是否能够确切而简介地反映工程问题的客观实际。在建立数学模型时，片面地强调确切，往往会使数学模型十分冗长、复杂，增加求解问题的困难程度，有时甚至会使问题无法求解；片面强调简洁，则可能使数学模型过分失真，以致失去了求解的意义。合理的做法是在能够确切反映工程实际问题的基础上力求简洁。设计变量、目标函数和约束条件是组成优化设计模型的三要素，下面分别予以讨论。

2 设计变量的选择

机械设计中的所以参数都是可变的，但是将所以的设计参数都列为设计变量不仅会使问题复杂化，而且是没有必要的。例如材料的机械性能由材料的种类决定，在机械设计中常用材料的种类有限，通常可根据需要和经验事先选定，因此诸如弹性模量、泊松比、许用应力等参数按选定材料赋以常量更为合理；另一类状态参数，如功率、温度、应力、应变、绕度、压力、速度、加速度等则通常可由设计对象的尺寸、载荷以及各构件间的运动关系等计算得出，多数情况下也没有必要作为设计变量。因此，在充分了解设计要求的基础上，应根据各设计参数对目标函数的影响程度认真分析其主次，尽量减少设计变量的数目，以简化优化设计问题。另外还应注意设计变量应当相当独立，否则会使目标函数出现“山脊”或“沟谷”，给优化带来困难。

3. 目标函数的确定

目标函数是一项设计所追求的指标的数学反映，因此对它最基本的要求是能够用来评价设计的优劣，同时必须是设计变量的可计算函数。选择目标函数是整个优化设计过程中最重要的决策之一。

有些问题存在明显的目标函数，例如一个没有特殊要求的承受静载的梁，自然希望它越轻越好，因此选择其自重作为目标函数是没有异议的。但涉及一台复杂的机器，追求的目标往往较多，就目前使用较成熟的优化方法来说，还不能把所有要追求的指标都列为目标函数，因为这样做并不一定能有效地求解。因此应当对所追求的各项指标进行细致的分析，从中选择最重要最具有代表性的指标作为设计追求的目标。例如一架好的飞机，应该具有自重轻、静载重量大、航程长、使用经济、价格便宜、跑道长度合理等性能，显然这些都是设计时追求的指标。但并不需要把它们都列为目标函数，在这些指标中最重要的指标是飞机的自重。因为采用轻的零部件建造的自身重量最轻的飞机只会促进其它几项指标，而不会损害其中任何一项。因此选择飞机自重作为优化的目标函数应该是最合适了。

若一项工程设计中追求的目标是互相矛盾的，这时常常取其中最主要的指标作为目标函数，而其余的指标列为约束条件。也就是说，不指望这些次要参数都达到最优，只要它们不至于过劣就可以了。

4 约束条件的确定

约束条件是就工程设计本身而提出的对设计变量取值范围的限制条件。和目标函数一样，它们也是设计变量的可计算函数。

如前所述，约束条件可分为性能约束和边界约束两大类。性能约束通常与设计原理有关，有时非常简单，如设计曲柄连杆机构时，按曲柄存在条件而写出的约束函数均为设计变量的线性显函数；有时却相当复杂，如对一个复杂的机构系统，要计算其中各构件的应力和位移，常采用有限元法，这时相应的约束函数为设计变量的隐函数，计算这样的约束函数往往要花费很大的计算量。

在选择约束条件时应当特别注意避免出现相互矛盾的约束。因为相互矛盾的约束必然导致可行域为一空集，使问题的解不存在。另外应当尽量减少不必要的约束，不必要的约束不仅增加优化设计的计算量，而且可能使可行域缩小，影响优化结果。

二、优化理论

1  综 述

优化理论归根到底是优化数学理论，机械优化设计是建立在多元函数的极值理论上的。主要包括以下几个方面的内容：

        多元函数的方向导数与梯度

        多元函数的泰勒展开

        无约束优化问题的极值条件

        凸集、凸函数与凸规划

        等式约束优化问题的极值条件

        不等式约束优化问题的极值条件

2  K-T条件

在以上众多理论中，K-T条件应用最为广泛，下面重点讨论一下K-T条件。

不等式约束多元函数极值条件：

 

用起作用约束的下标集合表示

 

用梯度形式表示，可得

K-T条件的几何意义：在约束极小点处，函数的负梯度一定能表示成所有起作用约束在该点梯度的非负线性组合。

三、优化算法

1. 无约束优化算法

1.1 概 述

无约束优化方法是优化技术中基本的也是非常重要的内容。无约束优化问题的数学模型如下：

 

使用无约束优化方法，不仅可以直接求无约束优化设计问题的最优解，而且通过对无约束优化方法的研究给约束优化方法建立明确的概念、提供良好的基础，某些优化设计方法就是先把约束优化设计问题转化为无约束问题后，再直接用无约束优化方法求解。无约束优化问题一般模型为

给定x(0)，置k=1

a)        确定局部下降方向d^(k),使▽f(x^(k))^Td^(k)<0；

b)        确定步长t^k>0,使f(x^(k)+t^kd^(k))<f(x^(k))；

c)        令x^(k+1)=x^(k)+t^kd^(k)；

d)        判断是否终止，终止则输出，否则k:=k+1，返回(a)

从上面的分析我们看到一个算法的搜索方向成为该优化方法的基本标志，分析、确定搜索方向d^(k)是研究优化方法的愚根本的任务之一。根据构成搜索方向使用的信息性质不同，无约束优化可以分为两类。一类是利用目标函数的一阶导数或二阶导数的无约束优化方法，如最速下降法、共轭梯度法、牛顿法等。另一类是只利用目标函数值得无约束优化算法，如坐标轮换法、单纯形法和鲍威尔法。下面将分别讨论。

1.2 最速下降法

    优化设计是追求目标函数值最小，因此，自然可以设想从某点出发，其搜索方向取该点的负梯度方向，使函数值在该点附近下降最快。这种方法也称为最速下降法。

1.2.1 基本原理

梯度法的迭代公式为：         

此式表明，相邻的两个迭代点的梯度是彼此正交的。也即在梯度的迭代过程中，相邻的搜索方向相互垂直。梯度法向极小点的逼近路径是锯齿形路线，越接近极小点，锯齿越细，前进速度越慢。这是因为，梯度是函数的局部性质，从局部上看，在该点附近函数的下降最快，但从总体上看则走了许多弯路，因此函数值的下降并不快。

1.2.2 算法流程

1.3 共轭梯度法

共轭梯度法是共轭方向法的一种，因为该方法中每一个共轭向量都是依赖于迭代点处的负梯度而构造出来的，所以称作共轭梯度法。

1.3.1 基本原理

共轭梯度法的搜索方向采用梯度法基础上的共轭方向，如图所示，目标函数F(x)在迭代点x^(k+1)处的负梯度为 ，该方向与前一搜索方向 互为正交，在此基础上构造一种具有较高收敛速度的算法，该算法的搜索方向要满足以下两个条件：

以x^(k+1)点出发的搜索方向是与的线性组合。即

以与为基底的子空间中，矢量与相共轭，即满足

1.3.2 算法流程

1.4 DFP变尺度法

变尺度法也称拟牛顿法，它是基于牛顿法的思想而又作了重大改进的一类方法。我们所介绍的变尺度法是由Davidon于1959年提出又经Fletcher和Powell加以发展和完善的一种变尺度法，故称为DFP变尺度法。

1.4.1 基本思想

变尺度法的基本思想与牛顿法和梯度法有密切联系。观察梯度法和牛顿法的迭代公式

和 

    分析比较这两种方法可知：梯度法的搜索方向为-g^(k) ，只需计算函数的一阶偏导数，计算量小，当迭代点远离最优点时，函数值下降很快，但当迭代点接近最优点时收敛速度极慢。牛顿法的搜索方向为- Hk-1 g(k) ，不仅需要计算一阶偏导数，而且要计算二阶偏导数及其逆阵，计算量很大，但牛顿法具有二次收敛性，当迭代点接近最优点时，收敛速度很快。

    若迭代过程先用梯度法，后用牛顿法并避开牛顿法的海赛矩阵的逆矩阵的烦琐计算，则可以得到一种较好的优化方法，这就是“变尺度法”产生的基本构想。为此，综合梯度法和牛顿法的优点，提出变尺度法的基本思想。变尺度法的基本迭代公式写为下面的形式：

1.4.2 算法流程

1.5 小结

    下面讨论本章所介绍的几种优化方法的适用范围：

可靠性：牛顿法较差，因为它对目标函数要求太高，解题成功率较低。

有效性：坐标变换法和梯度法的计算效率较低，因为它们从理论上不具有二次收敛性。

简便性：牛顿法和变尺度法的程序编制较复杂，牛顿法还占用较多的存储单元。

    由以上讨论可知，在选用无约束优化方法时，一方面要考虑优化方法的特点，另一方面要考虑目标函数的情况。

    1、一般而言，对于维数较低或者很难求得导数的目标函数，使用坐标轮换法或鲍威尔法较合适。

    2、对于二次性较强的目标函数，使用牛顿法效果好。

    3、对于一阶偏导数易求的目标函数，使用梯度法可使程序编制简单，但精度不宜过高。

4、综合而言，鲍威尔法和DFP法具有较好的性能。

2. 约束优化算法

2.1 惩罚函数法

2.1.1 基本思想

将有约束条件的优化问题转化为无约束优化问题来求解。

前提：一是不能破坏约束问题的约束条件，二是使其最优解归结到原约束问题的同一最优解上去。

 

构成一个新的目标函数，称为惩罚函数

根据惩罚项得不同构成形式，惩罚函数法又可分为外点惩罚函数法、内点惩罚函数法和混合惩罚函数法。

2.1.2 算法流程

2.2 拉格朗日乘子法

2.2.1 PH算法     

效用函数为

判断函数为

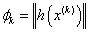
      当时迭代停止。

步骤1：选定初始点，初始拉格朗日乘子向量，初始罚因子及其放大系数，控制误差与常数，令。

步骤2：以为初始点，求解无约束问题：

得到无约束问题最优解

步骤3：当时，为所求的最优解，停；否则转步骤4.

步骤4：当时，转步骤5；否则令，转步骤5.

步骤5：令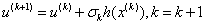，转步骤1。

2.2.2算法

松弛变量法：

乘子的修正公式为：

判断函数为：

当时迭代停止。

2.3 序列二次规划

2.3.1 基本思想

用牛顿法解L平稳点方程，每一步迭代又转化为求二次规划问题。

2.3.2 算法流程

 

2.4 小结

经过学习，我们可以对算法作简要总结，一般性方法：惩罚函数法，序列线性规划方法，可行方向法；最优秀的方法：增广拉格朗日乘子法，序列二次规划方法，简约梯度法；最常用的方法：序列线性规划方法，序列二次规划方法。

在实际应用中，我们应该具体问题具体分析，选择最合适研究对象的优化算法。

四、Matlab优化工具箱

在Matlab中，为求解优化问题开发了专门的优化工具箱（Optimization ToolBox），该工具箱的程序（M文件）位于目录toolbox\optim。Matlab的优化工具箱主要应用包括以下方面

   1. 求解无约束条件非线性极小值； 

   2. 求解约束条件下非线性极小值，包括目标逼近问题、极大-极小值问题；

   3. 求解二次规划和线性规划问题；

   4. 非线性最小二乘逼近和曲线拟合；

   5. 求解复杂结构的大规模优化问题

4.1 优化工具箱常用函数

4.2 优化工具箱结构

4.2 线性规划问题

  线性规划问题是目标函数和约束条件均为线性函数的问题。

线性规划问题的数学模型为：

min 

s.t. 

             

             

其中f、x、b、beq、lb、ub为向量，A、Aeq为矩阵。

其它形式的线性规划问题都可经过适当变换化为此标准形式。

函数  linprog

其调用格式很多，限于篇幅就不一一列举，仅作简单介绍：

x=linprog(f,A,b,Aeq,beq,lb,ub)  

%指定x的范围，若没有等式约束 ，则    Aeq=[ ]，beq=[ ]

[x,fval]=linprog(…)  

% 返回目标函数最优值，即fval=f^T*x。

4.3  非线性规划问题

4.3.1  无约束非线性规划问题

多元函数最小值的数学模型为：

其中：x为向量，如

可以使用函数fminbnd、fminsearch和fminunc。

函数  fminbnd

格式  x=fminbnd(fun,x1,x2,options)

          % options为指定优化参数选项

[x,fval] = fminbnd(…)  

    % fval为目标函数的最小值

函数  fminsearch

格式  x=fminsearch(fun,x0,options)  

          % options查optimset

[x,fval] = fminsearch(…) 

    %最优点的函数值

函数  fminunc

格式  x = fminunc(fun,x0,options)  

          % options为指定优化参数

[x,fval] = fminunc(…) 

    %fval最优点x处的函数值

4.3.2  约束非线性规划问题

非线性有约束的多元函数的数学模型为：

s.t.  

      

      

      

      

其中：x、b、beq、lb、ub是向量，A、Aeq为矩阵，C(x)、Ceq(x)是返回向  量的函数，f(x)为目标函数，f(x)、C(x)、Ceq(x)可以是非线性函数。

函数  fmincon

格式  x = fmincon(fun,x0,A,b,Aeq,beq,lb,ub)

[x,fval] = fmincon(…)

4.3.3  二次规划问题

二次规划问题的数学模型为：

s.t. 

          

          

其中，H、A、Aeq为矩阵，f、b、beq、lb、ub、x为向量

其它形式的二次规划问题都可转化为标准形式。

函数  quadprog

格式   x = quadprog(H,f,A,b,Aeq,beq)  

       [x,fval] = quadprog(…)  

            %fval为目标函数最优值

五、总 结

以上是我对自己学习过程的一个简要总结，经过八周的学习，我对工程优化有了初步的了解，掌握了一定处理工程问题的能力，希望能够在今后的科研工作中去应用，去深化。