求微分方程的解

一、实验目的及意义

1. 归纳和学习求解常微分方程(组)的基本原理和方法；
2. 掌握解析、数值解法，并学会用图形观察解的形态和进行解的定性分析；
3. 熟悉MATLAB软件关于微分方程求解的各种命令。

二、实验内容

1.         微分方程及方程组的解析求解法；

2.         微分方程及方程组的数值求解法——欧拉、欧拉改进算法；

3.         直接使用MATLAB命令对微分方程(组)进行求解(包括解析解、数值解)；

4.         利用图形对解的特征作定性分析。

三、实验步骤

1. 开启软件平台——MATLAB，开启MATLAB编辑窗口；
2. 根据微分方程求解步骤编写M文件
3. 保存文件并运行；
4. 观察运行结果(数值或图形)；
5. 根据观察到的结果和体会写出实验报告。

四、实验要求与任务

根据实验内容和步骤，完成以下实验，要求写出实验报告

1. 求微分方程的通解．

2. 求微分方程的通解．

3. 求微分方程组

在初始条件下的特解，并画出解函数的图形．

4. 分别用 ode23、ode45 求上述第 3 题中的微分方程初值问题的数值解(近似解)，求解区间为．利用画图来比较两种求解器之间的差异．

5. 用 Euler 折线法求解微分方程初值问题

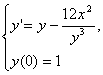
的数值解(步长h取0.1)，求解范围为区间[0,2]．

6. 用四阶 Runge-Kutta 法求解微分方程初值问题

的数值解(步长h取0.1)，求解范围为区间[0,3]．

五. 程序代码及运行结果（经调试后正确的源程序）

1. 求微分方程的通解．

程序代码：

syms x y

fprintf('通解为')

y=dsolve('(x^2-1)*Dy+2*x*y-sin(x)=0','x')

运行结果：

通解为

y =

(-cos(x)+C1)/(x^2-1)

2. 求微分方程的通解．

程序代码：

syms x y

fprintf('通解为')

y=dsolve('D2y-2*Dy+5*y=exp(x)*sin(x)','x')

运行结果：

通解为

y =

-1/4*exp(x)*cos(2*x)*sin(x)+1/12*exp(x)*cos(2*x)*sin(3*x)-1/12*exp(x)*sin(2*x)*cos(3*x)+1/4*exp(x)*sin(2*x)*cos(x)+C1*exp(x)*cos(2*x)+C2*exp(x)*sin(2*x)

3. 求微分方程组

在初始条件下的特解，并画出解函数的图形．

程序代码：

syms x y t

[x,y]=dsolve('Dx+x+y=0','Dy+x-y=0','x(0)=1','y(0)=0','t')

ezplot(x,y,[0,2]);

运行结果：

x =

1/2*exp(2^(1/2)*t)+1/4*2^(1/2)*exp(-2^(1/2)*t)-1/4*2^(1/2)*exp(2^(1/2)*t)+1/2*exp(-2^(1/2)*t)

y =

1/4*2^(1/2)*exp(-2^(1/2)*t)-1/4*2^(1/2)*exp(2^(1/2)*t)

4. 分别用 ode23、ode45 求上述第 3 题中的微分方程初值问题的数值解(近似解)，求解区间为．利用画图来比较两种求解器之间的差异．

程序代码：

M函数文件verderpol.m:

function xprime=verderpol(t,x)

xprime=[-x(1)-x(2); x(2)-x(1)];

在程序中调用此函数：

clear;

y0=[1;0];

[t,x]=ode45('verderpol',[0,2],y0); plot(x(:,1),x(:,2),'r-');

hold on

clear;

y0=[1;0];

[t,x]=ode23('verderpol',[0,2],y0); plot(x(:,1),x(:,2),'b-');

运行结果：

5. 用 Euler 折线法求解微分方程初值问题

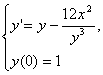
的数值解(步长h取0.1)，求解范围为区间[0,2]．

程序代码：

clear

f=sym('y-(12*x^2)/y^3');

a=0;  b=2;

h=0.1;

n=(b-a)/h+1;

x=0;  y=1;

szj=[x,y];

for i=1:n-1

    y=y+h*subs(f,{'x','y'},{x,y});

    x=x+h;

    szj=[szj;x,y];

end

szj

plot(szj(:,1),szj(:,2),'or-')

运行结果：

szj =

         0    1.0000

    0.1000    1.1000

    0.2000    1.2010

    0.3000    1.2934

    0.4000    1.3728

    0.5000    1.4359

    0.6000    1.4781

    0.7000    1.4921

    0.8000    1.4644

    0.9000    1.3662

    1.0000    1.1217

    1.1000    0.3836

    1.2000  -25.3054

    1.3000  -27.8358

    1.4000  -30.6193

    1.5000  -33.6812

    1.6000  -37.0492

    1.7000  -40.7541

    1.8000  -44.8294

    1.9000  -49.3123

    2.0000  -54.2435

6. 用四阶 Runge-Kutta 法求解微分方程初值问题

的数值解(步长h取0.1)，求解范围为区间[0,3]．

程序代码：

clear;

f=sym('y-exp(x)*cos(x)');

a=0; b=3; h=0.1;

n=(b-a)/h+1;

x=0; y=1; 

szj=[x,y];

for i=1:n-1

    l1=subs(f,{'x','y'},{x,y});

    l2=subs(f,{'x','y'},{x+h/2,y+l1*h/2});

    l3=subs(f,{'x','y'},{x+h/2,y+l2*h/2});

    l4=subs(f,{'x','y'},{x+h,y+l3*h});

    y=y+h*(l1+2*l2+2*l3+l4)/6;

    x=x+h;

    szj=[szj;x,y];

end

szj

plot(szj(:,1),szj(:,2), 'dg-')

运行结果：

szj =

         0    1.0000

    0.1000    0.9948

    0.2000    0.9787

    0.3000    0.9509

    0.4000    0.9109

    0.5000    0.8583

    0.6000    0.7933

    0.7000    0.7165

    0.8000    0.6290

    0.9000    0.5329

    1.0000    0.4309

    1.1000    0.3268

    1.2000    0.2256

    1.3000    0.1337

    1.4000    0.0590

    1.5000    0.0112

    1.6000    0.0021

    1.7000    0.0456

    1.8000    0.1582

    1.9000    0.3590

    2.0000    0.6702

    2.1000    1.1171

    2.2000    1.7283

    2.3000    2.5364

    2.4000    3.5774

    2.5000    4.8916

    2.6000    6.5231

    2.7000    8.5204

    2.8000   10.9359

    2.9000   13.8260

    3.0000   17.2510

六．实验总结

本次实验的目的是归纳和学习求解常微分方程(组)的基本原理和方法；掌握解析、数值解法，并学会用图形观察解的形态和进行解的定性分析；熟悉MATLAB软件关于微分方程求解的各种命令。实验中，我们了解和熟悉了微分方程及方程组的解析求解法；微分方程及方程组的数值求解法——欧拉、欧拉改进算法；直接使用MATLAB命令对微分方程(组)进行求解(包括解析解、数值解)以及利用图形对解的特征作定性分析。经过多次MATLAB实验，对MATLAB的语法也越来越熟悉，对相关的数学思想也有了更多了解。

                                 学生签名：          

七．教师评语及成绩

教师签名：           

                                                      年    月     日

 

第二篇：数学建模实验报告孤岛危机求解微分方程问题

求解微分方程问题

一.实验目的

建立微分方程模型，求出方程的解来说明实际现象，并加以检验，以此来研究实际问题的函数变化规律。

通过运用matlab软件及相关知识解决与讨论孤岛疾病微分方程问题。

二.实验内容

孤岛疾病问题

考虑在一个人口数量为N的孤岛上，一部分到岛外旅游的居民回来使该岛感染了一种高传染性的疾病。请预测在某时刻t将会被感染的人数X。考虑一下模型，其中k>0为常数：

(a)    列出这个模型所隐含的两条主要假设，说明这些假设有什么依据？

(b)   把X作为t的函数，解出前面给出的模型。

(c)   由(b)，当t趋于无穷时求X的极限。

(d)    设岛上的人口有5000人，在传染期的不同时刻被感染人数如下表

       问这些数据能否支持所给的模型？

(e)   画出关于X的图形

(f)    若初始被感染的人数，画出X关于t的图形；若初始被感染人数为，画出X关于t的图形。

(g) 利用(f)的结果估计模型中的常数，并预测t=ns天(ns为你学号最后两位数字+10)时被感染的人数。

(h) 分析上述模型的优缺点，试给出改进方案。

四. 模型求解（含经调试后正确的源程序）

a)

假设1人口数量N不变，因为是孤岛。

假设2人口分为健康人和被感染的病人数量分别为X ,N-X。

b)程序文件：b.m

syms N k;

X=dsolve('DX=k*X*(N-X)')

结果：

X =

 N/(1+exp(-k*N*t)*C1*N)

c)=N

d)

由上式可以看出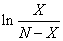是线性变化的，观察表中数据可得：这些数据能支持所给的模型。

e)程序文件：e.m

设k=0.1

ezplot('0.1*x*(1-x)',[0,1])

f)程序文件：f_1.m , f_2.m

时，取，则

y=dsolve(‘Dy=0.1*y*(1-y)’,y(0)=0.25’,’x’)

ezplot(y,[0,70])

  时取，则

y=dsolve('Dy=0.1*y*(1-y)','y(0)=0.75','x')

ezplot(y,[0,70])

g)程序文件：g.m

由可得k=0.5

再代入k值，得C₂=1.5，而N=5000，

当t=4+10=14时，可以解出X的值：

X= 4979

h)优点：将病人区分为两类：健康人和被感染的病人，且总人数不会改变。

不加控制最终每个人都会患病，而且传染强度有最大值。

缺点：没有考虑治愈问题等情况。

改进：将对象分为三类：病人，健康人与治愈的人。

六．实验总结

本次实验是利用微分方程求解现实生活中很难解决的事，孤岛危机只是其中一个小类，该类型的问题中，数学模型的建立是至关重要的，正确的作出模型为以后解题作准备，解题的方法不过是常微分方程的求解罢了，“desolve、solve”函数便能解决。

                                 学生签名：          

七．教师评语及成绩

教师签名：           

                                                      年    月     日