西安邮电大学

数学建模实验报告

最优捕鱼策略

投资的收益与风险问题

      姓名:           学号:

     江荣吉         04123049       

      周伟           04123040   

      张煜           04123043  

                                        计算机学院

                                         软件工程

                      

 

问题阐述

    生态学表明，对可再生资源的开发策略应在事先可持续收获的前提下追求最大经济效益。考虑具有4个年龄组：1龄鱼，…，4龄鱼的某种鱼。该鱼类在每年后4个月季节性集中产卵繁殖。而按规定，捕捞作业只允许在前8个月进行，每年投入的捕捞能力固定不变，单位时间捕捞量与各年龄组鱼群条数的比例称为捕捞强度系数。使用只能捕捞3、4龄鱼的13mm网眼的拉网，其两个捕捞强度系数比为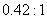。渔业上称这种方式为固定努力量捕捞。

      

该鱼群本身有如下数据：

    1、各年龄组鱼的自然死亡率为0.8（1/年），其平均质量为5.07,11.55,17.86,22.99（单位：g）；

    2、1龄鱼和2龄鱼不产卵，产卵期间，平均每条4龄鱼产卵量为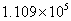（个），3龄鱼为其一半；

       3、卵孵化的成活率为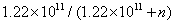（n为产卵总数）

      

有如下问题需要解决：

       1、分析如何实现可持续捕捞（即每年开始捕捞时渔场中各年龄组鱼群不变），并在此前提下得到最高收获量；

       2、合同要求某渔业公司在5年合同期满后鱼群的生产能力不能受到太大的破坏，承包时各年龄组鱼群数量为122， 29.7， 10.1， 3.29 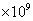（条），在固定努力量的捕捞方式下，问该公司应采取怎样的捕捞策略，才能使总收获量最高。

                        （二）模型假设

1．鱼在一年内的任何时间都会发生自然死亡，即死亡是一个连续的过程。

2．捕捞也是一个连续的过程，不是在某一时刻突然发生。

3．1、2龄鱼体形太小，不能被捕。

4．3、4龄鱼在一年中的后4个月的第一天集中一次产卵

5．i龄鱼到来年分别长一岁成为i+1龄鱼，i=1，2，3，其中上一年存活下来的4龄鱼仍是4龄鱼

                         （三）模型的建立

3.1问题分析

l  自然死亡率的理解：

本题中给出的鱼的自然死亡率是指平均死亡率，即单位时间鱼群死亡数量与现有鱼群数量的比例系数，它与环境等其它外在因素无关；这是一个有量纲的量，它既不是简单的百分率又不是简单的变化速率，实际上它是百分比率的变化率。它应该理解为以每年死亡80%的速率减少，并不是在一年内恰好死亡80%。另一方面，鱼群的数量是连续变化的，且1，2龄鱼在全年及3，4龄鱼在后4个月的数量只与死亡率有关。由此可知，各龄鱼的变化满足：

                 

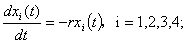
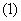
l  捕捞强度系数的理解：

捕捞强度系数是单位时间内捕捞量与各年龄组鱼群条数的比例系数，单位时间4龄鱼捕捞量与4龄鱼群总数成正比，捕捞强度系数是一定的，且只在捕捞期内（即每年的前8个月）捕捞3，4龄鱼。所以，捕捞强度系数k影响了3，4龄鱼在捕捞期内的数量变化：

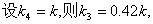
则有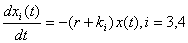                                 

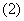
l  卵的成活率的理解：

1，2龄鱼不产卵，3，4龄鱼在每年的后四个月产卵，我们假设了在9月初一次产卵，因此可将每年的产卵量n表示为：

                 

     

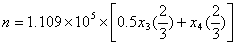
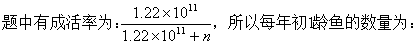
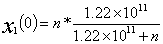
 3.2  模型的建立

4.2.1 问题一模型

1．由4.1.1中对自然死亡率的理解中的（1）式，可知1，2龄鱼的生长只受自然死亡率的影响，由此可知1，2龄鱼的生长的微分方程满足方程（1）：

                     

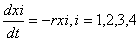
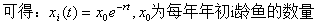
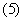
T年的i龄鱼在T+1年变为i+1龄鱼，

                    

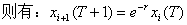
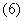
2．而对于3，4龄鱼的生长，在前八个月，他们的生长不仅受自然生长率的影响，还受捕捞强度系数的影响，而后四个月仅受自然生长率的影响。

我们以一年为一个时间单位，则这一时间单位可以分为两个阶段，捕捞期占2/3,产卵期占1/3.

   

    则

1. 前八个月3、4龄鱼生长的微分方程满足：

                   

             

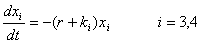
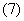
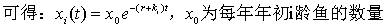
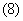
        由于每年的捕捞只在1到8月进行，并且只能捕到3，4龄鱼，所以任意一个时刻的捕捞量为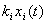，则年捕捞量为：

                     

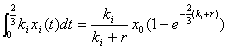
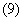
       2. 后四个月3、4龄鱼生长的微分方程满足方程（1）：

                    

               

                                

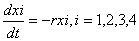
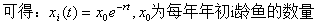
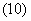
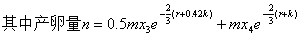
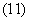
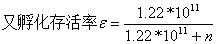
       所以年初1龄鱼的总量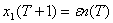                   

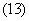
       3．根据以上分析，我们可以建立非线性规划模型：

  

 

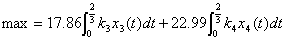
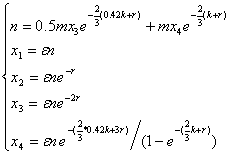
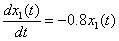                       t∈[0，1]，x1（0）= n ×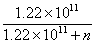

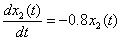                       t∈[0，1]，x2（0）= x1（1）

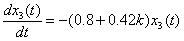                t∈[0，2/3]，x3（0）= x2（1）

    s.t. 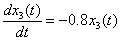                 t∈[2/3，1]，x3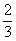（-）= x3（+）

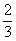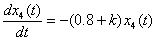                    t∈[0，2/3]，x4（0）= x3（1）

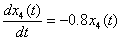                         t∈[2/3，1]，x4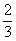（-）= x4（+）

           

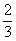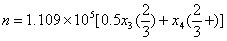
问题二模型

       

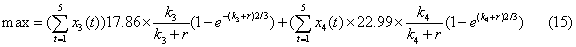
             关系式为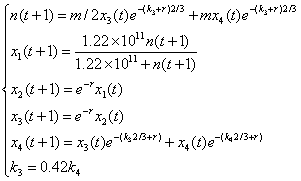

                        （四）模型求解

   我们可将目标函数和约束条件转化为：

目标函数为：

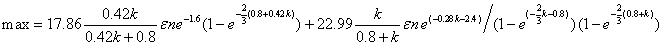
约束条件：

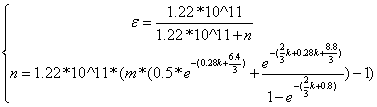
然后我们利用lingo软件和matlab软件分别进行求解。

1）lingo

直接运行，输出结果为：

Local optimal solution found at iteration:             92

  Objective value:                                0.3887076E+12

                       Variable           Value        Reduced Cost

                              K        17.36292           -1.034723

                              N       0.6078067E+13        0.000000

                            Row    Slack or Surplus      Dual Price

                              1       0.3887076E+12        1.000000

                              2        0.000000           0.1258406E-02

Matlab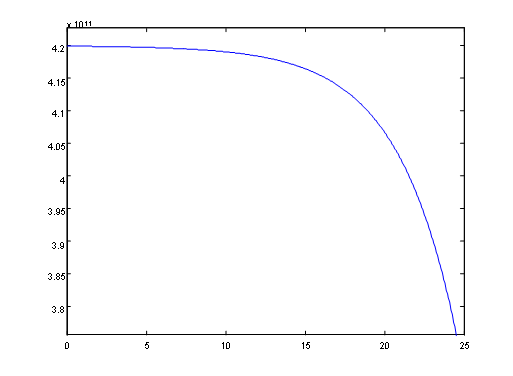

2.      可以看出捕捞强度对收获量的影响：

实验输出数据：

y =

 -3.6757e+011

y =

-3.9616e+011

y =

 -4.0483e+011

y =

-4.0782e+011

y =

-4.0802e+011

y =

-4.0805e+011

y =

-4.0805e+011

y =

-4.0805e+011

y =

-4.0805e+011

y =

-4.0805e+011

y =

-4.0805e+011

y =

     0

y =

-4.0667e+011

k =

  18.25976795085083

total =

    4.080548655562244e+011

a10 =

    1.195809275167686e+011

a20 =

  5.373117428928620e+010

a30 =

    2.414297288420686e+010

a40 =

8.330238542343275e+007

则k=18.25976795085083时，最高年收获量为4.080548655562244×10¹¹（克），此时每年年初1，2，3，4年龄组鱼的数量分别为：

1.195809275167686×10¹¹

5.373117428928620×10¹⁰

2.414297288420686×10¹⁰

8.330238542343275×10⁷

 

               （五）参考文献

姜启源、谢金星、叶俊,《数学模型（第四版）》高等教育出版社

    彭放  ，《数学建模方法》科学出版社

赵静，但琦《Mathematical modeling and mathematical experiments》高等教育出版社

人员分配：

收集资料  江荣吉

制图排版  张煜

分析计算  周伟

投资的收益与风险问题

市场上有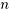种资产（如股票、债券、…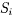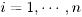）()供投资者选择，某公司有数额为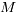的一笔相当大的资金可用作一个时期的投资。公司财务分析人员对这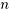种资产进行了评估，估算出在这一时期内购买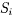的平均收益率为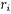，并预测出购买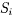的风险损失率为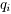。考虑到投资越分散，总的风险越小，公司确定，当用这笔资金购买若干种资产时，总体风险可用所投资的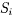中最大的一个风险来度量。

购买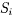要付交易费，费率为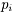，并且当购买额不超过给定值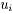时，交易费按购买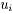计算（不买当然无须付费）。另外，假定同期银行存款利率是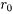, 且既无交易费又无风险。（）

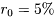已知时的相关数据如下：

试给该公司设计一种投资组合方案，即用给定的资金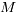，有选择地购买若干种资产或存银行生息，使净收益尽可能大，而总体风险尽可能小。

模型分析

　

本题需要我们设计一种投资组合方案，使收益尽可能大，而风险尽可能小。并给出对应的盈亏数据，以及一般情况的讨论。

这是一个优化问题，要决策的是每种资产的投资额，要达到目标包括两方面的要求:净收益最大和总风险最低，即本题是一个双优化的问题，一般情况下，这两个目标是矛盾的，因为净收益越大则风险也会随着增加，反之也是一样的，所以，我们很难或者不可能提出同时满足这两个目标的决策方案，我们只能做到的是：在收益一定的情况下，使得风险最小的决策，或者在风险一定的情况下，使得净收益最大，或者在收益和风险按确定好的偏好比例的情况下设计出最好的决策方案，这样的话，我们得到的不再是一个方案，而是一个方案的组合，简称组合方案。

设购买S_i （i=0,1…….n;S₀表示存入银行，）的金额为x_i;所支付的交易费为c_i(x_i)，则：

      

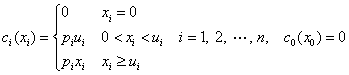
对S_i 投资的净收益为: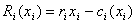　（i＝0，1，…，n）

对S_i投资的风险为: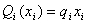　（i＝0，1，…，n），q₀=0

对S_i投资所需资金（即购买金额 x_i 与所需的手续费 c_i(x_i) 之和）是

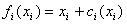　（i＝0，1，…，n）

投资方案用 x=（x₀，x₁，…，x_n）表示，那么，

净收益总额为：

 

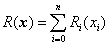
总风险为：

= 

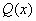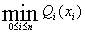
所需资金为：

                            

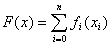
所以，总收益最大，总风险最小的双目标优化模型表示为：

                     

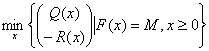
但是像这样的双目标模型用一般的方法很难求解出来的，所以经过分析把次模型转化为三种较简单的单目标模型。

模型假设

假设该公司在这一时期内是一次性投资；除交易费和投资费用外再无其他的费用开支；在这一时期市场发展基本上是稳定的；外界因素对投资的资产无较大影响；无其他的人为干预；社会政策无较大变化；公司的经济发展对投资无较大影响资产投资是在市场中进行的，市场是复杂多变的，是无法用数量或函数进行准确描述的，因此以上的假设是必要的，一般说来物价变化具有一定的周期性，社会政策也并非天天改变，公司自身的发展在稳定的情况下才会用额外的资金进行较大的风险的投资， 市场与社会的系统发展在一个时期内是良性的、稳定的，以上假设也是合理的。

模型建立

1）模型a

假设投资的风险水平是k,即要求总风险Q（x）限制在k内，Q（x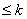），则模型可转化为：

max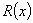

s.t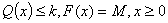 

2）模型b

假设投资的收益水平是h，即净收益总额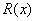不少于 h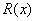：≥h，则模型可转化为：

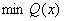
s.t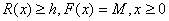

3）模型c

假设投资者对风险和收益的相对偏好参数为ρ（≥0），则模型可转化为：

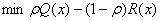
s.t.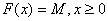

模型求解

由于交易费 c_i(x_i)是分段函数，使得上述模型中的目标函数或约束条件相对比较复杂，是一个非线性规划问题，难于求解. 但注意到总投资额 M 相当大，一旦投资资产 S_i，其投资额 x_i 一般都会超过 u_i，于是交易费 c_i(x_i)可简化为线性函数

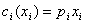
从而，资金约束简化为

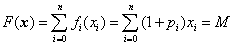
净收益总额简化为

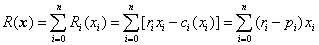
在实际进行计算时，可设 M=1，此时

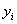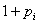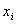 =（）（i＝0，1，…，n）

可视作投资 S_i 的比例.

以下的模型求解都是在上述两个简化条件下进行讨论的.

1）模型 a 的求解

模型 a 的约束条件 Q(x)≤k 即

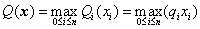≤k，

所以此约束条件可转化为

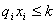　　（i＝0，1，…，n）.

这时模型 a 可化简为如下的线性规划问题：

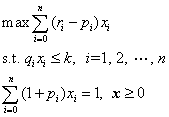
具体到 n=4 的情形，按投资的收益和风险问题中题中给定的数据，模型为：

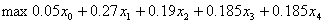
s.t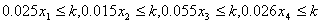

（i＝0，1，…，4）

利用matlab7.1 求解模型a

输出结果是

{0.177638, {x0 -> 0.158192, x1 -> 0.2, x2 -> 0.333333, x3 -> 0.0909091,x4 -> 0.192308}}

这说明投资方案为（0.158192，0.2，0.333333，0.0909091，0.192308）时，可以获得总体风险不超过 0.005 的最大收益是 0.177638M.

当 k 取不同的值（0~0.025），风险与收益的关系见图1.

输出结果列表如下：

表1 .模型1的计算结果

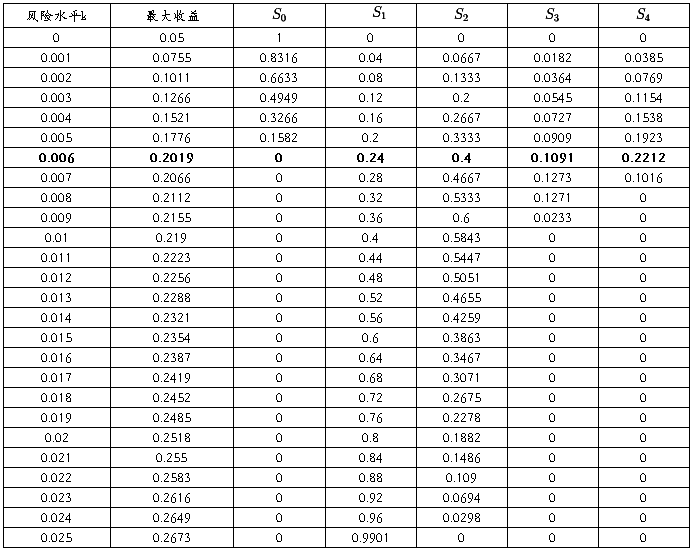
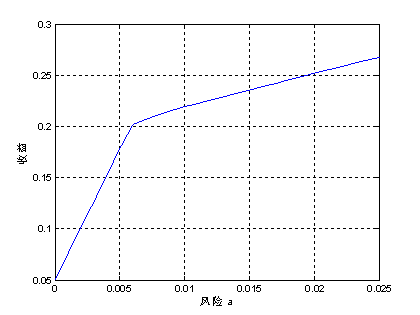
图1 .模型1中风险k与收益的关系

2）模型 b 的求解

模型 b 本来是极小极大规划：

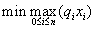
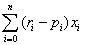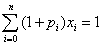s.t. ≥h　　　　x≥0

但是，可以引进变量 x_n+1=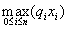，将它改写为如下的线性规划：

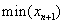
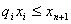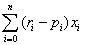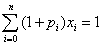s.t ,i=0,1,2,…,n,　≥h,　,　x≥0

具体到 n=4 的情形，按投资的收益和风险问题中题中给定的数据，模型为：

min x₅

s.t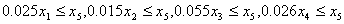

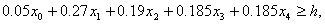
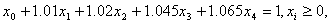（i＝0，1，…，5）

利用 matlab7.1 求解模型 b，当 h 取不同的值（0.1~0.25），我们计算最小风险和最优决策,收益水平h取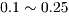，结果如表2所示，风险和收益的关系见图2.

表2 .模型2的计算结果

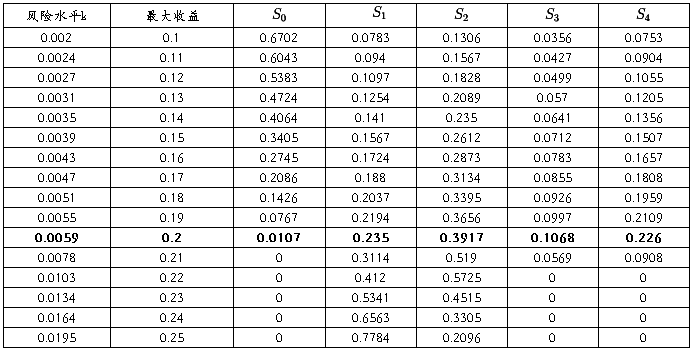
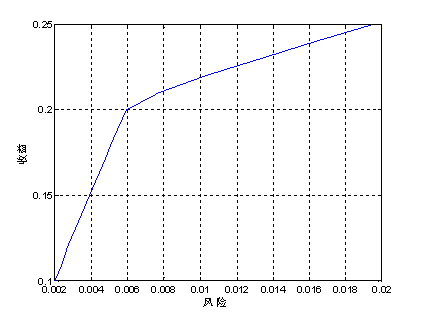
图2 .模型2中风险与收益h的关系

3）模型 c 的求解

类似模型 b 的求解，我们同样引进变量 x_n+1=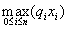，将它改写为如下的线性规划：

min ρx_n+1–（1–ρ）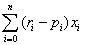

s.t 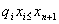,i=0，1，2，…，n　　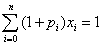　　x≥0

具体到 n=4 的情形，按投资的收益和风险问题题中给定的数据，模型为：

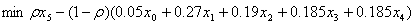
s.t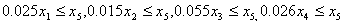

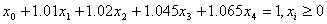（i＝0，1，…，5）

利用 matlab7.1 求解模型 c，当 ρ 取不同的值（0.75~0.95），我们计算最小风险和最优决策

输出结果列表如下：

表3 .模型3的计算结果

 

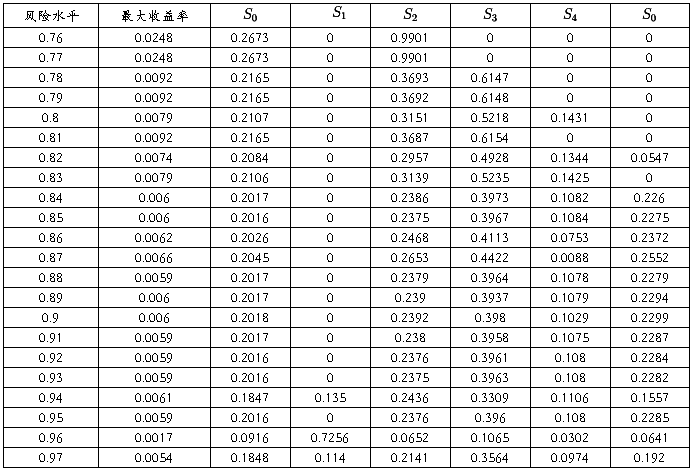
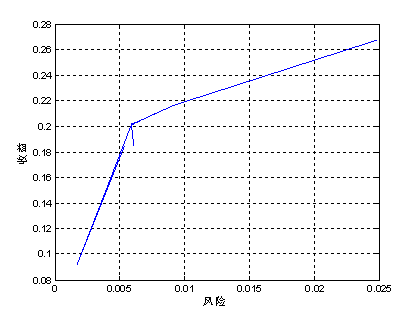
图3 .模型3中风险与收益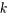的关系

 

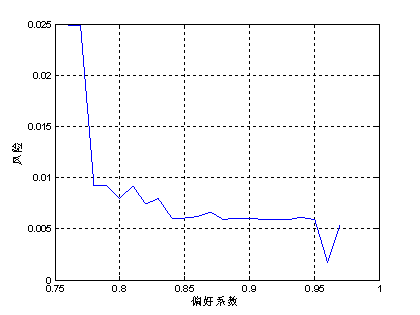
图4.模型3中风险与偏好系数的关系

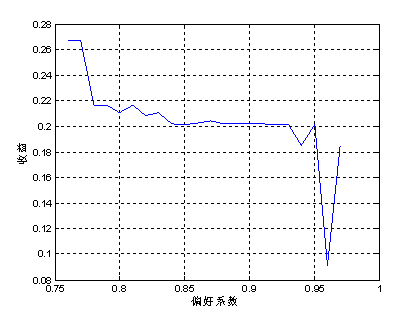
图5 .模型3中收益与偏好系数的关系

结果分析

1）结合图1，对于风险和收益没有特殊偏好的投资者来说，应该选择图中曲线的拐点（0.006，0.2019），这时对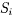的投资比例见表1的黑体所示。

2）从表1中的计算结果可以看出，对低风险水平，除了存入银行外，投资首选风险率最低的 S₂，然后是 S₁ 和 S₄，总收益较低；对高风险水平，总收益较高，投资方向是选择净收益率（r_i–p_i）较大的 S₁ 和 S₂．这些与人们的经验是一致的，这里给出了定量的结果．

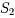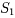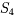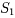3）从表2看出，对低收益水平，除了存入银行外，投资首选风险率最低的资产，然后是和，总收益当然较低。对高收益水平，总风险自然也高，应首选净收益率（）最大的和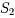。这些与人们的经验是一致的。

4）结合图2，对于风险和收益没有特殊偏好的投资者来说，应该选择图中曲线的拐点（0.059，0.2），这时对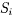的投资比例见表2的黑体所示。

5）从图5可以看出，模型3的风险与收益关系与模型1和模型2的结果几乎完全一致。

6）本文我们建立了投资收益与风险的双目标优化模型，通过控制风险使收益最大，保证收益使风险最小，以及引入收益——风险偏好系数，将两目标模型化为了单目标模型，并使用matlab7.1求解，所得结果具有一定的指导意义。

模型改进

本文没有讨论收益和风险的评估方法，在实际应用中还存在资产相关的情形，此时，用最大风险代表组合投资的风险未必合理，因此，对不同风险度量下的最优投资组合进行比较研究是进一步的改进方向。

结论

1.       风险大，收益也大；

2.       当投资越分散时，投资者承担的风险越小，这与题意一致，冒险的投资者会出现集中投资的情况，保守的投资者则尽量分散投资；

3.  曲线上的任一点都表示该风险水平的最大可能收益和该收益要求的最小风险。可以针对不同风 险的承受能力，选择该风险水平下的最优投资组合

参考文献

[1]MATLAB程序设计与实例应用。张铮等。北京：中国铁道出版社，2003.10
[2]运筹学—方法与应用。吴风平。南京：河海大学出版社，2000.12
[3]《数学模型及方法》。李火林主编。江西高校出版社，1997.10
[4]数学建模教育及竞赛。甘筱青主编。南昌：江西高校出版社。2004.6

[5]   萧树铁，面向21世纪课程教材：大学数学数学实验，北京：高等教育出版社，1999.7.

[6]赫孝良，戴永红等编著，数学建模竞赛：赛题简析与论文点评，西安：西安交通大学出版社，2002.6.

[7]陈叔平，谭永基，一类投资组合问题的建模与分析，数学的实践与认识，（29）7：45-49，1999.

人员分配：

收集资料  周伟

制图排版  张煜

分析计算  江荣吉