高三数学一轮复习每日一练7(解析版)
每日一练7
1.若函数 的定义域为R,则实数
的定义域为R,则实数 的取值范围 。
的取值范围 。 
2.已知曲线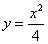 的一条切线的斜率为
的一条切线的斜率为 ,则切点的横坐标为( A )
,则切点的横坐标为( A )
A.1 B.2 C.3 D.4
3.要得到函数 的图象,只需将函数
的图象,只需将函数 的图象( A )
的图象( A )
A.向右平移 个单位 B.向右平移
个单位 B.向右平移 个单位
个单位
C.向左平移 个单位 D.向左平移
个单位 D.向左平移 个单位
个单位
4.已知数列{ }的前
}的前 项和
项和 ,第
,第 项满足
项满足 ,则
,则 ( )
( )
A.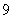 B.
B. C.
C.  D.
D.
5.已知两个等差数列 和
和 的前
的前 项和分别为A
项和分别为A 和
和 ,且
,且 ,则使得
,则使得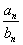 为整数的正整数
为整数的正整数 的个数是( )
的个数是( )
A.2 B.3 C.4 D.5
6.已知函数 (x>0)在x = 1处取得极值
(x>0)在x = 1处取得极值 ,其中a,b,c为常数。
,其中a,b,c为常数。
(1)试确定a,b的值;
(2)讨论函数f(x)的单调区间;
(3)若对任意x>0,不等式 恒成立,求c的取值范围。
恒成立,求c的取值范围。
解:(I)由题意知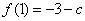 ,因此
,因此 ,从而
,从而 .
.
又对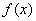 求导得
求导得
 .
.
由题意 ,因此
,因此 ,解得
,解得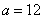 .
.
(II)由(I)知 (
(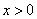 ),令
),令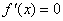 ,解得
,解得 .
.
当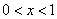 时,
时, ,此时
,此时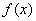 为减函数;
为减函数;
当 时,
时, ,此时
,此时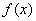 为增函数.
为增函数.
因此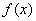 的单调递减区间为
的单调递减区间为 ,而
,而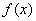 的单调递增区间为
的单调递增区间为 .
.
(III)由(II)知,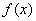 在
在 处取得极小值
处取得极小值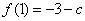 ,此极小值也是最小值,要使
,此极小值也是最小值,要使 (
(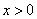 )恒成立,只需
)恒成立,只需 .
.
即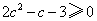 ,从而
,从而 ,
,
解得 或
或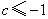 .所以
.所以 的取值范围为
的取值范围为 .
.
第二篇:20xx届高三数学一轮复习专讲专练 :7.6 直接证明与间接证明
巩固双基,提升能力
一、选择题
1.若P=+,Q=+(a≥0),则P、Q的大小关系是( )
A.P>Q B.P=Q
C.P<Q D.由a的取值确定
解析:∵要证P<Q,只要证P2<Q2,
只要证:2a+7+2<2a+7+2,
只要证:a2+7a<a2+7a+12,
只要证:0<12,
∵0<12成立,
∴P<Q成立.
答案:C
2.设x,y,z∈(0,+∞),a=x+,b=y+,c=z+,则a,b,c三数( )
A.至少有一个不大于2 B.都小于2
C.至少有一个不小于2 D.都大于2
解析:a+b+c=x++y++z+≥6,
因此a,b,c至少有一个不小于2.
答案:C
3.要使-<成立,则a,b应满足( )
A.ab<0且a>b
B.ab>0且a>b
C.ab<0且a<b
D.ab>0且a>b或ab<0且a<b
解析:要使-<成立,
只要(-)3<()3成立,
即a-b-3+3<a-b成立,
只要<成立,
只要ab2<a2b成立,
即要ab(b-a)<0成立,
只要ab>0且a>b或ab<0且a<b成立.
答案:D
4.设0<a<b,a+b=1,则下列不等式中正确的是( )
A.b<2ab<<a2+b2
B.2ab<b<a2+b2<
C.2ab<a2+b2<<b
D.2ab<a2+b2<b<
解析:方法一:由条件,得a2+b2>2ab,>=b,
b-(a2+b2)=b(1-b)-a2=ab-a2=a(b-a)>0,
故b>a2+b2,∴2ab<a2+b2<b<.
方法二:特值法,令a=,b=.
答案:D
5.已知a>b>0,且ab=1,若0<c<1,p=logc,q=logc2,则p、q的大小关系是( )
A.p>q B.p<q
C.p=q D.p≥q
解析:∵>ab=1,∴p=logc<0.
又q=logc2=logc
>logc=logc>0,
∴q>p.
答案:B
6.已知函数f(x)=x,a,b∈R+,A=f,B=f(),C=f,则A、B、C的大小关系是( )
A.A≤B≤C B.A≤C≤B
C.B≤C≤A D.C≤B≤A
解析:≥≥,又函数f(x)=x在(-∞,+∞)上是单调递减函数,
∴f≤f()≤f.
答案:A
二、填空题
7.在等比数列{an}和等差数列{bn}中,a1=b1>0,a3=b3>0,a1≠a3,则a5和b5的大小关系为________.
解析:方法一:设公比为q,公差为d,
则a3=a1q2,b3=b1+2d=a1+2d,
故由a3=b3,得2d=a1(q2-1).
又∵a1≠a3,∴q2≠1.
∴a5-b5=a1q4-(a1+4d)
=a1q4-[a1+2a1(q2-1)]
=a1(q2-1)2>0.
∴a5>b5.
方法二:∵在等比数列{an}中,a1≠a3,
∴公比不为1.∴a1≠a5.
又∵a1=b1,a3=b3,a5=a3q2>0(q为公比),
∴b3==a3=<=.
∴a5>b5.
答案:a5>b5
8.若a,b,c为Rt△ABC的三边,其中c为斜边,那么an+bn与cn(其中n∈N*且n>2)的大小关系是__________.
解析:方法一:△ABC为直角三角形,且c为斜边,
则c2=a2+b2,
∴c>a>0,c>b>0,即0<<1,0<<1.
当n>2时,
n+n<2+2==1,
即an+bn<cn.
方法二:特值法,令c=,a=b=1.
答案:an+bn<cn
9.已知点An(n,an)为函数y=的图像上的点,Bn(n,bn)为函数y=x图像上的点,其中n∈N*,设cn=an-bn,则cn与cn+1的大小关系为__________.
解析:an=,bn=n.
方法一:cn=-n=随n的增大而减小,为减函数,
∴cn+1<cn.
方法二:cn+1=-(n+1),
cn=-n,
∴==>1.
∴cn>cn+1.
答案:cn>cn+1
三、解答题
10.已知非零向量a,b,且a⊥b,求证:≤.
解析:∵a⊥b,∴a·b=0,
要证≤,只需证|a|+|b|≤|a+b|,
只需证|a|2+2|a||b|+|b|2≤2(a2+2a·b+b2),
只需证|a|2+2|a||b|+|b|2≤2a2+2b2,
只需证|a|2+|b|2-2|a||b|≥0,
即(|a|-|b|)2≥0,上式显然成立,故原不等式得证.
11.设f(x)=3ax2+2bx+c,若a+b+c=0,f(0)>0,f(1)>0,求证:a>0且-2<<-1.
解析:∵f(0)>0,∴c>0,
又∵f(1)>0,即3a+2b+c>0①
而a+b+c=0即b=-a-c代入①式,
∴3a-2a-2c+c>0,即a-c>0,∴a>c.
∴a>c>0.
又∵a+b=-c<0,a+b<0.
∴1+<0.∴<-1.
又c=-a-b,代入①式得,
3a+2b-a-b>0,∴2a+b>0.
∴2+>0.
∴>-2.故-2<<-1.
综上,a>0且-2<<-1.
12.已知a,b,c∈R,a+b+c=0,abc=1,求证:a,b,c中至少有一个大于.
解析:∵abc=1,
∴a,b,c三者得同为正或一正两负;
又∵a+b+c=0,
∴a,b,c三者中只能是一正两负.
不妨设a>0,b<0,c<0,则b+c=-a,又bc=,
∴b,c为方程x2+ax+=0的两个负根.
∴Δ=a2-≥0.
∴a≥ > =.
∴a>.
-
高三数学第一轮复习教学反思
高考在即第一轮复习已经接近尾声这里就一轮复习谈谈自己的一点反思高考是选拔性的考试对于数学学科来说它是在考查学生基础知识的同时突出能…
-
高三一轮复习总结反思
制定出自己的复习计划作家柳青曾讲过人生的道路虽然漫长但紧要处却往往只有几步走好了会影响你的一生寒假虽然短却是个难得自由支配时间利用…
-
高三数学一轮复习精品资料——基础知识归纳(整理)
高三数学一轮复习基础知识归纳第一部分集合1理解集合中元素的意义是解决集合问题的关键元素是函数关系中自变量的取值还是因变量的取值还是…
-
高三数学一轮复习资料——知识归纳
高三数学一轮复习基础知识归纳第一部分集合1理解集合中元素的意义是解决集合问题的关键元素是函数关系中自变量的取值还是因变量的取值还是…
-
高三第一轮复习总结及下阶段计划
20xx届数学第一轮复习总结及下阶段工作计划经过一学期我们数学基本完成了第一轮复习现在把第一轮复习总结和下阶段计划简述如下一确立复…
-
人教版高三数学一轮复习:1.集合概念与运算
知识点总结1.含义与表示:(1)集合中元素的特征:确定性,互异性,无序性(2)集合的分类:有限集,无限集(3)集合的表示法:列举法…
-
高三一轮复习总结反思
制定出自己的复习计划作家柳青曾讲过人生的道路虽然漫长但紧要处却往往只有几步走好了会影响你的一生寒假虽然短却是个难得自由支配时间利用…
-
高三第一轮复习总结及下阶段计划
20xx届数学第一轮复习总结及下阶段工作计划经过一学期我们数学基本完成了第一轮复习现在把第一轮复习总结和下阶段计划简述如下一确立复…
-
20xx高考数学第一轮知识点总结
一20xx数学高考复习直线与方程知识点葫芦岛朗曼外语总结直线与方程就是直线的方程在几何问题的研究中我们常常直接依据几何图形中点直线…
-
高三数学一轮复习资料——知识归纳
高三数学一轮复习基础知识归纳第一部分集合1理解集合中元素的意义是解决集合问题的关键元素是函数关系中自变量的取值还是因变量的取值还是…