数学物理方程报告
平流方程.这个方程是:
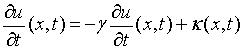 (1)
(1)
其中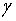 是一个正常数,
是一个正常数,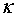 是
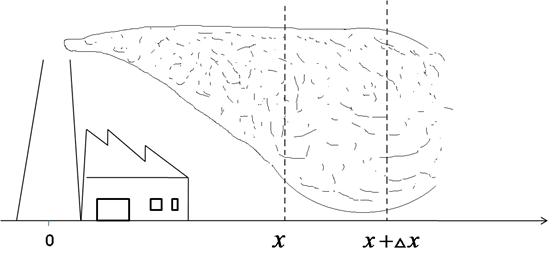
是 的函数.这个方程可以用来模拟艾滋病的传播、流体动力学,以及其他有关空气或水中的物质流动问题.作为具体的应用,考察风的运动,假设风沿着某个方向运动,比如
的函数.这个方程可以用来模拟艾滋病的传播、流体动力学,以及其他有关空气或水中的物质流动问题.作为具体的应用,考察风的运动,假设风沿着某个方向运动,比如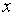 轴的正方向,其速度为每秒
轴的正方向,其速度为每秒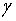 米.设在原点处有一工厂,风从工厂处携带一些污染物.令
米.设在原点处有一工厂,风从工厂处携带一些污染物.令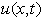 表示
表示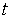 时刻
时刻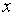 处的污染物的(线)密度(每米的颗粒个数).再设污染颗粒以正比于
处的污染物的(线)密度(每米的颗粒个数).再设污染颗粒以正比于 的速度掉下来,比例常数是
的速度掉下来,比例常数是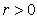 ,则
,则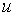 满足方程(1),
满足方程(1), .
.
(a)试证方程
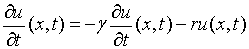
的所有解都具有形式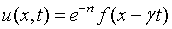 .
.
(b)令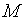 是初始时刻空气中的总颗粒数.试证:在时刻
是初始时刻空气中的总颗粒数.试证:在时刻 空气中的总颗粒数是
空气中的总颗粒数是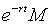 .
.
--------------------------------------------------------------------------
对于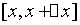 段
段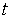 到
到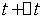 时间段内的颗粒物数有以下关系
时间段内的颗粒物数有以下关系
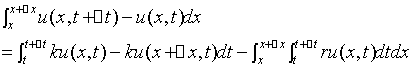
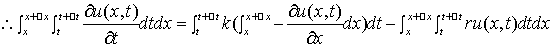
由于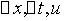 任意性知
任意性知
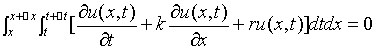
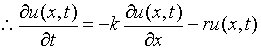
----------------------------------------------------------------------------
推导过程
 为风速
为风速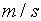 ,
,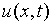 为
为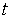 时刻
时刻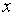 处的污染的(线)物密度(每米的颗粒个数),则
处的污染的(线)物密度(每米的颗粒个数),则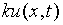 为单位时间内
为单位时间内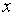 处的颗粒数
处的颗粒数
----------------------------------------------------------------------------------------------
研究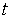 到
到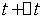 段通过
段通过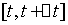 短的颗粒物。
短的颗粒物。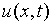 为
为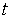 时刻
时刻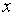 处的颗粒物(线)密度
处的颗粒物(线)密度
 为
为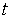 时刻
时刻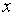 到
到 段内的颗粒物
段内的颗粒物
----------------------------------------------------------------------------------------
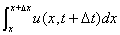 为
为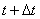 的间段
的间段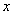 到
到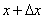 段内的颗粒物
段内的颗粒物
从而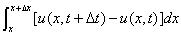 表示
表示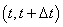 时间段内
时间段内
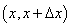 段颗粒物的变化量
段颗粒物的变化量
则 为
为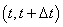 时间段内吹过
时间段内吹过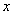 处的颗粒物
处的颗粒物
则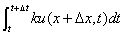 为
为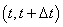 时间段内吹过
时间段内吹过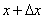 处的颗粒物
处的颗粒物
污染颗粒以正比于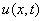 的速度下落比例常数为
的速度下落比例常数为
则下落速度为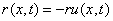
从而在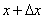 段内
段内 到
到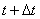 的间段下落的颗粒物总数
的间段下落的颗粒物总数
为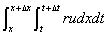
由于总颗粒物的变化量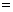 吹入
吹入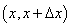 的颗粒物
的颗粒物 吹出
吹出
的颗粒物 下落的颗粒物
下落的颗粒物
 可得
可得
第二篇:数学物理方程
第一章.波动方程
§1方程的导出。定解条件
1.细杆(或弹簧)受某种外界原因而产生纵向振动,以u(x,t)表示静止时在x点处的点在时刻t离开原来位置的偏移,假设振动过程发生的张力服从虎克定律,试证明u(x,t)满足方程
???u????u??ρ(x)?=?E??t??t??x??x?
其中ρ为杆的密度,E为杨氏模量。
证:在杆上任取一段,其中两端于静止时的坐标分别为x与x+?x。现在计算这段杆在时刻t的相对伸长。在时刻t这段杆两端的坐标分别为:
x+u(x,t);x+?x+u(x+?x,t)
其相对伸长等于
令[x+?x+u(x+?x,t)]?[x+u(x,t)]??x=ux(x+θ?x,t)?x?x→0,取极限得在点x的相对伸长为ux(x,t)。由虎克定律,张力T(x,t)等于
T(x,t)=E(x)ux(x,t)
其中E(x)是在点x的杨氏模量。
设杆的横截面面积为S(x),则作用在杆段(x,x+?x)两端的力分别为
E(x)S(x)ux(x,t);E(x+?x)S(x+?x)ux(x+?x,t).
于是得运动方程ρ(x)s(x)??x?utt(x,t)=ESux(x+?x)|x+?x?ESux(x)|x
利用微分中值定理,消去?x,再令?x→0得
ρ(x)s(x)utt=
若s(x)=常量,则得?(ESux)?x
?2u??uρ(x)2=(E(x))?t?x?x
即得所证。
2.在杆纵向振动时,假设(1)端点固定,(2)端点自由,(3)端点固定在弹性支承上,试分别导出这三种情况下所对应的边界条件。解:(1)杆的两端被固定在x=0,x=l两点则相应的边界条件为
u(0,t)=0,u(l,t)=0.
(2)若x=l为自由端,则杆在x=l的张力T(l,t)=E(x)
同理,若x=0为自由端,则相应的边界条件为?u|x=l等于零,因此相应的边界条件为?x?u|x=l=0?x?u∣x=0=0?x
(3)若x=l端固定在弹性支承上,而弹性支承固定于某点,且该点离开原来位置的偏移由函数v(t)给出,则在x=l端支承的伸长为u(l,t)?v(t)。由虎克定律有
E?u∣x=l=?k[u(l,t)?v(t)]?x
?u+σu)∣x=l=f(t)?x其中σ=其中k为支承的刚度系数。由此得边界条件(k
E
01
特别地,若支承固定于一定点上,则v(t)=0,得边界条件
(?u+σu)∣x=l=0。?x
同理,若x=0端固定在弹性支承上,则得边界条件
即?u∣x=0=k[u(0,t)?v(t)]?x?u(?σu)∣x=0?f(t).?xE
?x2?ux2?2u3.试证:圆锥形枢轴的纵振动方程为E[(1?=ρ(1??xh?xh?t2
其中h为圆锥的高(如图1)
证:如图,不妨设枢轴底面的半径为1,则x
点处截面的半径l为:
l=1?
所以截面积s(x)=π(1?xhx2。利用第1题,得h
x2?2u?x?uρ(x)π(1?=Eπ(1?2]2h?t?xh?x
若E(x)=E为常量,则得
?x2?ux2?2u]=ρ(1?E[(1??xh?xh?t2
4.绝对柔软逐条而均匀的弦线有一端固定,在它本身重力作用下,此线处于铅垂平衡位置,试导出此线的微小横振动方程。解:如图2,设弦长为l,弦的线密度为ρ,则x点处的张力T(x)为
T(x)=ρg(l?x)
且T(x)的方向总是沿着弦在x点处的切线方向。仍以u(x,t)表示弦上各点在时刻t沿垂直于x轴方向的位移,取弦段(x,x+?x),则弦段两端张力在u轴方向的投影分别为
ρg(l?x)sinθ(x);ρg(l?(x+?x))sinθ(x+?x)
其中θ(x)表示T(x)方向与x轴的夹角又
于是得运动方程sinθ≈tgθ=?u?x.
?u?2u?uρ?x2=[l?(x+?x)]∣x+?xρg?[l?x]∣xρg?x?t?x
利用微分中值定理,消去?x,再令?x→0得
?2u??u=g[(l?x)。?t2?x?x
5.验证u(x,y,t)=1
t?x?y222在锥t2?x2?y2>0中都满足波动方程
?2u?2u?2u=+?t2?x2?y2
证:函数u(x,y,t)=1
t2?x2?y2在锥t2?x2?y2>0内对变量x,y,t有
2
二阶连续偏导数。且??u=?(t2?x2?y2)2?t?t
?3
23?2u
?t2=?(t2?x2?y2)
?+3(t2?x2?y2)?52?t2=(t?x?y)22232?(2t2+x2+y2)
??u2222=(t?x?y)?x?x3
?2u
?x2
2=t?x?2(2232?2y)+3t?x?(2252?2y)x2
同理)(t2+2x2?y2)5?2u222?22=(t?x?y)(t?x2+2y2)2=t?x??y
?2u
?x2+?2u
?y2=t?x?(52?2y所以(2252?2y)(2t2+x2+y2)=?
2u.?t
?u,故(x,x+?x)上?t2即得所证。6.在单性杆纵振动时,若考虑摩阻的影响,并设摩阻力密度涵数(即单位质量所受的摩阻力)与杆件在该点的速度大小成正比(比例系数设为b),但方向相反,试导出这时位移函数所满足的微分方程.解:利用第1题的推导,由题意知此时尚须考虑杆段(x,x+?x)上所受的摩阻力.由题设,单位质量所受摩阻力为?b
所受摩阻力为
?b?p(x)s(x)??x?u
?t运动方程为:
ρ(x)s(x)?x??2u?u?u??u?=ES??x+?x?ESx?b?ρ(x)s(x)?x?x?t??t??t2
利用微分中值定理,消去?x,再令?x→0得
ρ(x)s(x)
若s(x)???u??u?2u=.?ES??bρ(x)s(x)2?x??x??t?t=常数,则得
ρ(x)?u?2u???u?=?E??bρ(x)2?t?t?x??x?
若ρ(x)=ρ是常量,E(x)=E也是常量.令a2=
2?2u?u2?u.+b=a?t2?t?x2E,则得方程ρ
1.§2达朗贝尔公式、波的传抪证明方程
?????1??x???
的通解可以写成2x??u?1??=2?1?h??x??a?x??2u(hf0常数)?h??t22
3
u=Fx?at)+G(x+at)
h?x
?u=Ψ(x).?t其中F,G为任意的单变量可微函数,并由此求解它的初值问题:t=0:u=?(x),
解:令(h?x)u=v则
?v?(h?x)?u=u+?v,(h?x)2?u=(h?x)??u+??x?x?x??x?
??u?v?u?u?2v[(h?x)2=?(u+)+(h?x)+(h?x)2=(h?x)(u+2?x?x?x?x?x?x
又
代入原方程,得?2u?2v(h?x)2=2?t?t
(h?x)?
即2v?x2=1?2v(h?x)a2?t2?2v1?2v=?x2a2?t2
由波动方程通解表达式得
v(x,t)=F(x?at)+G(x+at)
所以
为原方程的通解。
由初始条件得u=F(x?at)+G(x+at)h?x1[F(x)+G(x)]h?x
1ψ(x)=?aF/(x)+aG/(x)h?x?(x)=(1)[]
(2)所以1F(x)?G(x)=ax0∫(α?h)ψ(α)dα+cx
由(1),(2)两式解出
11F(x)=(h?x)?(x)+(α?h)ψ(α)dα+c∫22ax2ox
11G(x)=(h?x)?(x)?22a
所以xo∫(α?h)ψ(α)dα+2xcu(x,t)=1h?x+at)?(x?at)+(h?x?at)?(x+at)]2(h?x)
+x+at1(h?α)ψ(α)dα.2a(h?x)∫x?at
即为初值问题的解散。
2.问初始条件?(x)与ψ(x)满足怎样的条件时,齐次波动方程初值问题的解仅由右传播波组成?解:波动方程的通解为
4
u=F(x-at)+G(x+at)
其中F,G由初始条件?(x)与ψ(x)决定。初值问题的解仅由右传播组成,必须且只须对于任何x,t有G(x+at)≡常数.
即对任何x,G(x)≡C0
又G(x)=11?(x)+22a∫x
x0ψ(α)dα?C2a
所以?(x),ψ(x)应满足
?(x)+
或1xψ(α)dα=C1(常数)a∫x01?'(x)+(x)=0a
2??2u2?u?t2=a?x2??ux?at=0=?(x)?u=ψ(x).?x+at=0?3.利用传播波法,求解波动方程的特征问题(又称古尔沙问题)(?(0)=ψ(0))
解:u(x,t)=F(x-at)+G(x+at)
令x-at=0
令x+at=0
所以得?(x)=F(0)+G(2x)得ψ(x)=F(2x)+G(0)F(x)=ψ(-G(0).
G(x)=?()-F(0).
且
所以F(0)+G(0)=?(0)=ψ(0).u(x,t)=?(x2x2x+atx?at)+ψ(-?(0).22
即为古尔沙问题的解。
4.对非齐次波动方程的初值问题
2??2u2?ua(t>0,?∞<x<+∞)=f(x,t)?2??t2?x???t=0,u=?(x),?u=ψ(x)(?∞<x<+∞)???t
证明:
(1)如果初始条件在x轴的区间[x1,x2]上发生变化,那末对应的解在区间[x1,x2]的影响区域以外不发生变化;
(2)在x轴区间[x1,x]上所给的初始条件唯一地确定区间[x1,x2]的决定区2
域中解的数值。
证:(1)非齐次方程初值问题的解为u(x,t)=11[?(x?at)+?(x+at)]+22a
x+a(t?τ)1∫x?a(t?τ)f(ξ,τ)dξdτ.2a∫0t∫x+atx?atψ(α)dα++
当初始条件发生变化时,仅仅引起以上表达式的前两项发生变化,即仅仅影晌到相应齐次方程初值的解。
5
当?(x),ψ(x)在[x1,x2]上发生变化,若对任何t>0,有x+at<x1或x-at>x2,则区间[x-at,x+at]整个落在区间[x1,x2]之外,由解的表达式知u(x,t)不发生变化,即对t>0,当x<x1-at或x>x2+at,也就是(x,t)落在区间[x1,x2]的影响域
xt?at≤x≤x2+at(t>0)
之外,解u(x,t)不发生变化。(1)得证。
(2).区间[x1,x2]的决定区域为t>0,x1+at≤x≤x2?at
在其中任给(x,t),则
x1≤x?at<x+at≤x2
故区间[x-at,x+at]完全落在区间[x1,x2]中。因此[x1,x2]上所给的初绐
条件?(x),βψ(x)代入达朗贝尔公式唯一地确定出u(x,t)的数值。
5.若电报方程
uxx=CLutt+(CR+LG)ut+GRu
(C,L,R,G为常数)具体形如
u(x,t)=?(t)f(x?at)
的解(称为阻碍尼波),问此时C,L,R,G之间应成立什么关系?
解u(x,t)=?(t)f(x?at)
uxx=?(t)f′′(x?at)
ut=?′(t)f(x?at)?a?(t)f′(x?at)
utt=?′′(t)f(x?at)?2a?′(t)f′(x?at)+a2?(t)f′′(x?at)
代入方程,得
(CLa?1?(t)f′′(x?at)?(2aCL?′(t)+a(CR+LG)?(t))f′(x?at)
+(CL?′′(t)+(CR+LG)?′(t)+GR?(t))+GR?(t)f(x?at)=02)
由于f是任意函数,故f,f′,f′′的系数必需恒为零。即
?CLa2?1=0??2CL?′(t)+(CR+LG)?(t)=0
?CL?′′(t)+(CR+LG)?′(t)+GR?(t)=0?
于是得CL=1
a2
u′(t)a2
=?(CR+LG)ut2
所以u(t)=c0ea2CR+LG)t2
代入以上方程组中最后一个方程,得
CL?
又
即2a4(CR+LG)2?a(CR+LG)2+GR≡042a2=112,得(CR+LG)=GRCLCL4=0
6(CR?LG)2
最后得到CG=LR
?utt=a2uxx??ut=0=?(x),utt=0=0ψ(x)(0<x<∞)?()?u0,t=0(t≥0)6.利用波的反射法求解一端固定并伸长到无穷远处的弦振动问题
解:满足方程及初始条件的解,由达朗贝尔公式给出:
11u(x,t)=(?(x+at)+?(x?at))+22ax+atx?at∫ψ(α)dα。
由题意知?(x),ψ(x)仅在0<x<∞上给出,为利用达朗贝尔解,必须将?(x),ψ(x)开拓到?∞<x<0上,为此利用边值条件,得
0=1
2()at?(at+?(at))+
?∫ψ(α)dα。at
因此对任何t必须有
?(at)=??(?at)
at)dα=0
?∫ψ(αat
即?(x),ψ(x)必须接奇函数开拓到?∞<x<0上,记开拓后的函数为Φ(x),Ψ(x);
Φ(x)=???(x),x>0
?Ψ(x)=??ψ(x),x>0
??(?x),x<0??ψ(?x),x<0
所以
?x+at
x+at1(?(x+at)+?(x?at))+1∫ψ(α)
u(x,t)=12(?(x+at)+?(x?at))+1
2a=?22adα,
?x?at
x∫ψ(α)dα?at?1(1x+at
?(x+at)??(at?x))+ψ(α)dα,
?22aat∫?x
?2u2?2u?2
7.求方程2??uu?
?t?形如u=f(r,t)的解(称为球面波)其中r=x2+y2+2
2=a???x2+?y2+?z2??z。
?
解:u=f(r,t)
?u?u
?x=?r??r
?x=?ur
?r?x
22
`?u?2ux2?u?1x
?x2=?r2?r2+?r??
?r?
?r3???
?2u?2uy2?u?
?y=?r?r+?r?1
??y2?
?rr???
?2u?2uz2
?z=?rr+?u
?r(1
r?z2
?r代入原方程,得
?2u?2u?u3x2+y2+z2
2
?t2=a[?r2+?r(r?r3即?2u2
?t2=a2(?u?r2+2r+?u
?r令ru=v,则
7t<xa,x>0。t>xa,x>0
r?2u?2v?u?v?2u?u?2v=r+=u+r=,2?t2?t2?r?r?r2?r?r2
代入方程,得v满足
2?2v2?v=a?t2?r2
故得通解
所以v(r,t)=F(r?at)+G(r+at)1u=F(r?at)+G(r+at)r
8.求解波动方程的初值问题
??2u?2u?2=tsinx?2??t?x??u?u=0,|t=0=sinxt=0???t
解:由非齐次方程初值问题解的公式得
x+ttx+(t?τ)11u(x,t)=∫sinαdα+∫∫τsinξdξdτ2x?t20x?(t?τ)
=?11t
[cos(x+t)?cos(x?t)]?∫τ[cos(x+(t?τ))?cos(x?(t?τ))]dτ220
t
=sinxsint+sinxτsin(t?τ)dτ
t=sinxsint+sinx[τcos(t?τ)+sin(t?τ)]0∫
=tsinx
即u(x,t)=tsinx为所求的解。
9.求解波动方程的初值问题。
tx?utt=a2uxx+?(1+x2)2???u|=0,u|=1
t=0tt=0?1+x2?
解:1u(x,t)=2a
x+atx+atx?at1+α∫12dα+∫ξτdξdτ22(1)+ξ0x?a(t?τ)tx+a(t?τ)∫1dα=arctg(x+at)?arctg(x?at)21+αx?at∫
ξτ?1x+a(t?τ)ξττ[dd=∫∫(1+ξ2)2∫2(1+ξ2)x?a(t?τ)dτ0x?a(t?τ)0
=
xtx+a(t?τ)t1tττ[?dτ2∫1+(x+a(t?τ)21+(x+a(t?τ))20x11x+at?ux?at?u=dudu+∫2?2∫22x?ata(1+u)2x+ata(1+u2)?1=2a2x+atx?ut∫1+u2du+zax?atdut∫1+u2+2ax?atxdu2x+at1+ux∫
8
x11+(x+at)2=(arctg(x?at)?arctg(x+at))+2ln2a24a1+(x?at)2t[2arctgx?arctg(x?at)?arctg(x+at)]2a
11=(x?at)arctg(x?at)?2(x+at)arctg(x+at)22a2a+
t11+(x+at)2
+arctgx+lna4a21+(x?at)2
所以
1{(x?at?2a2)arctg(x?at)?(x+at?2a2)?34a
11+(x+at)2
?arctg(x+at)+2atarctgx+ln21+(x?at)2u(x,t)=
§3混合问题的分离变量法
1.用分离变量法求下列问题的解:(1)
2??2u2?u?2=a?x2??t
3πx?u?,?ut=0=sinl?t??u(0,t)=u(l,t)=0??t=o=x(1?x)(0<x<l)
解:边界条件齐次的且是第一类的,令
u(x,t)=X(x)T(t)
得固有函数Xn(x)=sinnπx,且l
anπanπTn(t)=Ancost+Bnsint,(n=1,2L)ll
于是u(x,t)=∑(A
n=1∞ncosanπanπnπt+Bnsint)sinxlll
今由始值确定常数An及Bn,由始值得
sin3πx∞nπ=∑Ansinxlln=1
x(l?x)=∑
所以anπnπBnsinxlln=1∞A3=1,An=0,当n≠3
2Bn=anπ
=2
anπl∫x(l?x)sin0nπxdxl??l2nπx?+xcosx???nπl???lnπl2nπl??xcosx+sin??ln2π2l??nπ
2l2xnπ2l3nπ?22sinx?33cosxnπlnπl
因此所求解为)}l04l3=44(1?(?1)n)anπ
9
u(x,t)=cos3aπ3π4l3
tsinx+4llaπ1?(?1)nanπnπsintsinx∑4nlln=1∞
(2)2??2u2?u?a=0?22?t?x???u(0,t)=0
??u(x,0)=hx,?l??u(l,t)=0?t?u(x,0)=0?t
解:边界条件齐次的,令
u(x,t)=X(x)T(t)
得:?
及?X′′+λX=0?X(0)=0,X′(l)=0(2)。(1)T′′+a2λX=0
求问题(1)的非平凡解,分以下三种情形讨论。1oλ<0时,方程的通解为
X(x)=C1e
由X(0)=0得c1+c2=0
由X′(l)=0得C1?λe??+C2e???C2λe??=0
解以上方程组,得C1=0,C2=0,故λ<0时得不到非零解。2oλ=0时,方程的通解为X(x)=c1+c2x由边值X(0)=0得c1=0,再由X′(l)=0得c2=0,仍得不到非零解。3oλ>0时,方程的通解为
X(x)=c1cosx+c2sinx
由X(0)=0得c1=0,再由X′(l)=0得
c2cosl=0
为了使c2≠0,必须cosl=0,于是
2n+1?λ=λn=?π??2l??
且相应地得到Xn(x)=sin2(n=0,1,2L)2n+1πx2l(n=0,1,2L)
将λ代入方程(2),解得
Tn(t)=Ancos
∞2n+12n+1aπt+Bnsinaπt2l2l(n=0,1,2L)
于是
再由始值得u(x,t)=∑(Ancosn=02n+12n+12n+1aπt+Bnsinaπt)sinπx2l2l2l
10
∞2n+1?hx=Ansinπx∑??l2ln=0?∞?0=∑2n+1aπBnsin2n+1πx?2l2l?n=0
容易验证?sin
l??2n+1?πx?(n=0,1,2L)构成区间[0,l]上的正交函数系:2l??2m+12n+1?0当m≠nxsinπxdx=?l当m=n2l2l??2∫sin0
利用?sin?
?2n+1?πx?正交性,得2l?
2lh2n+1An=∫sinπxdxl0l2l
2h?2l2n+1?2l?=2??xcosπx+??l?(2n+1)π2l?(2n+1)π?
=8h
(2n+1)π?2n+1???sinx??2l???02l(?1)n
Bn=0
所以8h∞(?1)n2n+12n+1u(x,t)=2∑cosaπtsinx2πn=0(2n+1)2l2l
2。设弹簧一端固定,一端在外力作用下作周期振动,此时定解问题归结为
2??2u2?u=a??t2?x2?u(l,t)=Asinωt?u(0,t)=0,
??u?u(x,0)=?t(x,0)=0?求解此问题。解:边值条件是非齐次的,首先将边值条件齐次化,取U(x,t)=Axsinωt,则U(x,t)满足l
U(0,t)=0,U(l,t)=Asinωt
令u(x,t)=U(x,t)+v(x,t)代入原定解问题,则v(x,t)满足
2??2vAω2
2?v??t2=a?x2+lxsinωt
?v(l,t)=0?v(0,t)=0,
??vAω(x,0)=?x?v(x,0)=0?tl?(1)
v(x,t)满足第一类齐次边界条件,其相应固有函数为Xn(x)=sin
故设nπx,(n=0,1,2L)lv(x,t)=∑Tn(t)sin
n=1∞nπxl(2)
Aω2Aωnπ?将方程中非齐次项xsinωt及初始条件中?x按?x?展成级数,得?sinlll??
11
∞Aω2nπxsinωt=∑fn(t)sinxlln=1
其中2lAω2nπfn(t)=∫xsinωtsinxdxl0ll
?l2Aω2nπl2nπ?=sinωt?xcosx+sinx??l2ln2π2l?0?nπ
2Aω2Aω=(?1)n+1sinωt?xnπl
=∑ψnsin
n=1∞lnπxl
其中?2lAω2nπ2Aωψn=xsinxdx=(?1)n∫l0llnπ
2?2Aω2?anπ?′′T(t)+?(?1)n+1sinωt??Tn(t)=?nnπ?l?将(2)代入问题(1),得Tn(t)满足??T(0)=0,T′(0)=2Aω(?1)n
nn?nπ?
解方程,得通解Tn(t)=Ancosanπanπ2A?2sin?tt+Bnsint+(?1)n+1?anπ2llnπ(??2
l
由始值,得An=0
Bn=12A?(?1)n+12A?3l2(?1)n2A?al?1)n?=anπnπnπ((anπ)2??2l2)(anπ)2??2l2所以v(x,t)=∑{
n=1∞(?1)n2A?alanπsint(anπ)2?(?l)2l
(?1)n+12A?2l21nπ+?sin?t}sinx(anπ)2?(?l)2nπl
(?1)2anπ?lnπ=2A?l∑asint?sin?t}sinx22lnπln=1(anπ)?(?l)∞
因此所求解为
u(x,t)=∞A(?1)2
xsin?t+2A?l∑22ln=1(anπ)?(?l)
×{asinanπ?lnπt?sin?t}sinxlntl
3.用分离变量法求下面问题的解
2??2u2?u??t2=a?x2+bshx??u?|t=0=0?u|t=0=?t??u|x=0=u|x=l=0??
解:边界条件是齐次的,相应的固有函数为
Xn(x)=sinnπxl(n=1,2,L)
12
设u(x,t)=∑Tn(t)sin
n=1∞nπxl
将非次项bshx按{sinnπx}展开级数,得l
∞
bshx=∑fn(t)sin
n=1nπxl
其中2blnπ(?1)n+1
fn(t)=shxsinxdx=2bnπshll∫lnπ+l0
将u(x,t)=∑Tn(t)sin
n=1∞nπx代入原定解问题,得Tn(t)满足l
anπ22bnπ?′′Tn(t)=(?1)n+1
222shl?Tn(t)+(lnπ+l???Tn(0)=0,Tn′(0)=0
方程的通解为
Tn(t)=Ancosanπanπl22bnπt+Bnsint+(?(?1)n+1shlllanπnπ+l
l22bnπ22(?1)n+1shl2anπnπ+l由Tn(0)=0,得:An=?(
由Tn′(0)=0,得Bn=0
所以
所求解为Tn(t)=(122bnπanπ22(?1)n+1shl(1?cost)2anπnπ+ll
u(x,t)=∞2bl2(?1)n+1anπnπshl(1?cost)sinx∑2222aπlln=1n(nπ+l)
4.用分离变量法求下面问题的解:
2??2u?u2?u+2b=a(b>0)??t22?t?x???u|x=0=u|x=l=0
?h?u?u|t=0=x,|=0?l?tt=0?
解:方程和边界条件都是齐次的。令
u(x,t)=X(x)T(t)
代入方程及边界条件,得
T"+2bT'X"
==?λa2TX
X(0)=X(l)=0
由此得边值问题
?X"+λX=0??X(0)=X(l)=0
?nπ?,相应的固有函数为因此得固有值λ=λn=???l?2
Xn(x)=sinnπx,n=1,2,Ll
13
又T(t)满足方程
T"+2bT'+a2λT=0
将λ=λn代入,相应的T(t)记作Tn(t),得Tn(t)满足
T"n?anπ?+2bTn+??T=0?l?'
22一般言之,b很小,即阻尼很小,故通常有anπ?b<???,n=1,2,L?l?2
故得通解Tn(t)=e?bt(Ancosωnt+Bnsinωnt)
?anπ?ωn=???b2
?l?
∞2其中所以
u(x,t)=e?bt∑(Ancosωnt+Bnsinωnt)sin
n=1nπxl
再由始值,得∞?hnπx?x=∑Ansinl?ln=1?∞?0=(?bA+Bω)sinnπx∑nnn?l?n=1所以
2hlnπ2hAn=∫xsin=(?1)n+1
lnπl0
Bn=
所求解为b2bhAn=(?1)n+1ωnnπωn
2h?bt∞(?1)n+1bnπu(x,t)=e∑ωnt+sinωnt)sinx.πnωnln=1
§4高维波动方程的柯西问题
1.利用泊松公式求解波动方程
utt=a2(uxx+uyy+uzz)
的柯西问题
解:泊松公式32??ut=0=x+yz???utt=0=0
????1φ?1ψu=?+?∫∫r∫∫r?t?4πaM4πaM?SatSat??
现ψ=0,φ=x3+y2z
Φds=∫∫Φ(r,θ,?)rsinθdθd?|r=at∫∫Mr00satπ2π且
其中Φ(r,θ,?)=Φ(x+rsinθcos?,y+rsinθsin?,z+rcosθ)
14
=(x+rsinθcos?)3+(y+sinθsin?)2(z+rcosθ)
=x3+y2z+3x2rsinθcos?+3xr2sin2θcos2?+r2sin3θcos3?
+2yzrsinθsin?+rzsin2θsin2?+y2rcosθ
+2yr2sinθcosθsin?+r3sinθsin2?cosθ
π2π
计算∫∫Φ(r,θ,?)rsinθdθd?
00
π2π
∫∫(x
003+y2z)rsinθdθdψ=r(x3+y2z)?2π(?cosθ)π0
32=4πr(x+yz)
π2π
∫∫3x
002rsinθcos??rsinθdθd?=3xr22π∫sin0
322πθdθ∫cos?d?=003π2π
∫∫3xr
002sinθcos??rsinθdθd?=3xr22π∫sin0θdθ∫cos2?d?02π1φ1π=3xr3[cos3θ?cosθ]π+sin2φ]2
0?[0324
=4xrπ∫
π3π2π00∫r3sinθcos3??rsinθdθd?2π
=r
π2π4∫0sinθdθ4∫cos3?d?=4πxr3π
222π0∫∫2yzrsinθsin??rsinθdθd?=2yzr∫sin
000θdθ∫sin?d?=00
2ππ2ππ
2223∫∫r
00zsinθsin??rsinθdθd?=rz∫sinθdθ∫sin2?d?00
1?14π=r3z[cos3θ?cosθ]π?sin2?]2=r3z0?[03243
π2ππ
22π∫∫y
00rcosθ?rsinθdθd?=yr22∫cosθsinθdθ∫d?=000
π2π
∫∫2yr
002sinθcocθsin???rsinθdθd?
π2π
23=2yr
π2π∫sin0θcosθdθ∫sin?d?=00
∫∫r003sin2θsin2?cosθ?rsinθdθd?
π2π
3=r
所以4∫sin0θcosθdθ?∫sin2?d?=00
∫∫rMSatΦ4ds=[4πr(x2+y2z)+4πr3+πr3z]r=at3
1=4πat[x2+y2z+xa2t2+a2t2z]3
15
u(x,y,z)=?1Φ??t4πa∫∫Mr
Sat
?31[tx+ty2z+xa2t3+a2t2z]?t3
=x3+y2z+3a2t2x+a2t2z=
即为所求的解。
2.试用降维法导出振动方程的达朗贝尔公式。解:三维波动方程的柯西问题
2??utt=a(uxx+uyy+uzz)???ut=0=?(x,y,z),utt=0=φ(x,y,z)
当u不依赖于x,y,即u=u(z),即得弦振动方程的柯西问题:
2??utt=auzz???ut=0=?(z),utt=0=φ(z)
利用泊松公式求解
u=?1?1?ds}+ds∫∫∫∫?t4πaMr4πaMr
SatSat
因只与z有关,故
?∫∫rds=
MSat2ππ∫∫?(z+atcos?)?(at)2sinθdθd?at00
2ππ
=∫d?∫?(z+atcosθ)atsinθdθ
00
令z+atcos =α,-atsin d =d α
得
所以z+at?ds=2π∫?(α)dα∫∫Mrz?atSat
?1z+at1z+at
u(z,t)=?(α)dα+φ(α)dα∫?t2az∫2a?atz?at
11z+at
={?(z+at)+?(z?at)}+∫atφ(α)dα22az?
即为达郎贝尔公式。
3.求解平面波动方程的柯西问题:
2??utt=a(uxx+uyy)?2??u|t=0=x(x+y)ut|t=0=0
解:由二维波动方程柯西问题的泊松公式得:
?1??u(x,y,t)=?2πa??t∫∫m?∑at?(ζ,η)at?ζ?x?η?y2222dζdη
+
∑at∫∫mψ(ζ,η)a2t2?ζ?x2?η?y2??dζdη???
16
1?at
=2πa?t∫0
又2π∫0?(x+rcosθ,y+rsinθ)at?r222rdrdθ?(x+rcosθ,y+rsinθ)=(x+rcos)2(x+y+rcosθ+rsinθ)
=x2(x+y)+2x(x+y)rcosθ+(x+y)r2cos2θ
+x2r(cosθ+sinθ)+2xr2(cosθ+sinθ)cosθ
+r3cos2θ(cosθ+sinθ)
2π2π2π
2因为∫cosθdθ=0,∫sinθdθ=0,∫cos
000
2π2π
3θdθ=π2π∫sinθcosθdθ=0,∫cos
00θdθ=0,∫cos2θsinθdθ=0.0
at2π所以∫∫00?(x+rcosθ,y+rsinθ)at?r
at
2222θat=2πx(x+y)∫0rdra2t2?r2+π(3x+y)∫0r3dra2t2?r2
at
又∫0
atrdra2t2?r2=?a2t2?r2|at0=atat
2∫0r3drt?r22=?r2t?r|+2∫a2t2?r2rdr0222at0
2=?a2t2?r2
3(32|a
0=233at3
于是u(x,y,t)=1??233?2?2πax(x+y)+πa(3x+y)?2πa?t?3?
=x2(x+y)+a2t2(3x+y)
即为所求的解。
4.求二维波动方程的轴对称解(即二维波动方程的形如u=u(r,t)的解,r=x2+y2).
解:解法一:利用二维波动方程柯西问题的积分表达式
u(x,y,t)=
+1?[2πa?t∫∫at?ζ?x?η?y∑m?(ζ,η)dζdη222att∫∫at?ζ?x?η?y∑mψ(ζ,η)dζdη222att
由于u是轴对称的u=u(r,t),故其始值?,ψ只是r的函数,,u=|t=0=?(r),ut|t=0=ψ(r),又∑at为圆(ζ?x)2+(η?y)2≤a2t2.记圆上任一点p(ζ,η)的矢径为ρm
ρ=2+η2圆心M(x,y)其矢径为r=x2+y2记s=
oM与Mp的夹角。选极坐标(s,θ)。ζ?x)2+(η?y)2则由余弦定理知,ρ2=r2+s2?2rscosθ,其中θ为
17
?(ζ,η)=?(ρ)=?r2+s2?2rscosθ
r2+s2
2πψ(ζ,η)=ψ(ρ)=ψ1u(x,y,t)=2πa
at?2rscosθ)at)2?s2于是以上公式可写成??at?∫?t??02π∫0?r2+s2?2rscosθθ
?+∫0∫0ψr2+s2?2rscosθat2?s2)θ??
由上式右端容易看出,积分结果和(r,t)有关,因此所得的解为轴对称解,即
1?at2π?r2+s2+2rscosθu(r,t)=[sdsdθ2πa?t∫0∫0(at)2?s2
at2π
+∫∫00ψ(2+s2?2rcosθ(at)2?s2θ]
解法二:作变换x=rcosθ,y=rsinθ.波动方程化为
2?2u1?u2?u=a(+??t2?r2r?r
用分离变量法,令u(r,t)=R(r)T(t).代入方程得
"2??T+aλt=0?2"'2??rR+rR+λrR=0
解得:
??T(t)=Aλcosat+Bλsinaλt???R(r)=J0(r)
令=?叠加得
∞
u(r,t)=∫(A(?)cosα?t+B(?)sinα?t)J0(?γ)du
5.求解下列柯西问题
?vtt=a2(vxx+vyy)+c2v???v=ψ(x,y)?vt=0=?(c,y),?rt=0?
cz
[提示:在三维波动方程中,令
解:令
则czau(x,y,z)=eav(x,y,t)]u(x,y,z,t)=ev(x,y,t)utt=
uzzczeavtt,uxxcz=czeavxx,uyy=czeavyyc2=2eava
?utt=a2(uxx+uyy+uzz)?czcz?
aa?u?t=0=e?(x,y),utt=0=eψ(x,y)代入原问题,得
(ξ,η)?11ea(ξ,η)u(x,y,z,t)={}+∫∫∫∫?t4πaS4πaSMM
atatcζcζ
18
MSat:(ξ?x)2+(η?y)2+(ζ?z)2=a2t2
M+M?记Sat为上半球,Sat为下半球,∑M
atM为Sat在ξoη平面上的投影。
ds=
cζ
eaatat?(ξ?x)?(η?y)?(ξ,η)ds=r
ecξ2222dξdη,则MSat∫∫M+Sat∫∫1a1e?(ξ,η)ds+∫∫ea?(ξ,η)dsrrSM?atcξ=
∑at∫∫Mcz+a2t2?(ξ?x)2?(η?y)2)aa2t2?(ξ?x)2?(η?y)2
ec(z?a2t2?(ξ?x)2?(η?y)2)22(ξ,η)dξdη+∑at
cz
∫∫Mat?(ξ?x)?(η?y)ch
∑at22(ξ,η)dξdη=2e∫∫Mca2t2?(ξ?x)2?(η?y)2a(ξ,η)dξdη2222at?(ξ?x)?(η?y)
chc2t2?(r)2
a=2e∫∫(x+rcosθ,y+rsinθ)rdrdθ222at?r00cz2πata
所以u(x,y,z)=?1e?t2πacz2πat∫∫00cchc2t2?(r)2aa2t2?r2(x+rcosθ,y+rsinθ)tftfθ}+
cchc2t2?()2
1a(x+rcosθ,y+rsinθ)rdrdθe∫∫2πaa2t2?r200cz2πata
于是v(x,y,t)=??1?∫?t?2πa∫002πatcchc2t2?(r)2aa2t2?r2
1
2πa2πat(x++rcosθ,y+rsinθ)rdrdθ}+
+rcosθ,y+rsinθ)rdrdθ
即为所求的解。
6.试用∫∫00cchc2t2?(r)2aat?r222(x+?4第七段中的方法导出平面齐次波动方程
utt=a2(uxx+uyy)+f(x,y,t)
在齐次初始条件
u
下的求解公式。t=0=0,utt=0=0
解:首先证明齐次化原理:若w(x,y,t,τ)是定解问题
19
2??wtt=a(wxx+wyy)???wt=o=0,wt=τf(x,y,τ)
t
的解,则u(x,y,t)=∫w(x,y,t,τ)dτ即为定解问题
2??utt=a(uxx+uyy)+f(x,y,t)???ut=0=0,utt=0=0
的解。显然,ut=0=0
t
τ=t+∫0?u=w(x,y,t,τ)?t
(wt=τ=0).所以
又t?w?wτ=∫τ?t?t0?u?tt=0=0?2w+∫2τ?t0
?2wτ2?y0tt?2u?w=?t2?tτ=t=f(x,y,t)+∫
t?2ut?2w?2u?2w=τ,=0τ2∫22∫2?x?x?y?y0
因为w满足齐次方程,故u满足
2?2u?2u
2?u=f(x,y,t)+a(2+2?t2?x?y
齐次化原理得证。由齐次方程柯西问题解的泊松公式知
w(x,y,t,τ)=
所以12πa∑a(t?τ)
a(t?τ)2πM∫∫f(ζ,η,τ)2(t?τ)2?(ζ?x)2?(η?y)2ζdη1t
u(x,y,t)=2πa∫0
即为所求的解。所以∫∫00f(x+rcosθ,y+rsinθ,τ)a2(t?τ)2?r2θu(x,y,t)=1ta(t?τ)2πf(x+rcosθ,y+rsinθ,τ)rdrdθdτ∫02222πa∫0∫0a(t?τ)?r
7.用降维法来解决上面的问题解:推迟势
u(x,y,z,t)=1
4πa2∫∫∫
r≤atrf(ξ,η,t?r
其中积分是在以(x,y,z)为中心,at为半径的球体中进行。它是柯西问题
2??utt=a(uxx+uyy+uzz)+f(x,y,z,t)???ut=0=0,utt=0=0
的解。对于二维问题u,f皆与z无关,故
rf(ξ,η,t?1au(x,y,t)=2∫∫∫4πa0SM?rrat
20
其中srM为以M(x,y,0)为中心r为半径的球面,即
SrM:(ξ?x)2+(η?y)2+ζ2=r2
ds=r
r2?(ξ?x)2?(η?y)2
rf(ξ,η,t?=rdξdη∫∫SrM∫∫SrM+rrf(ξ,?,t?f(ξ,η,t?)+∫∫rrSrM?
=2
r∑M∫∫rf(ξ,η,t?aζdη2?(ξ?x)2?(η?y)2
其中srM+,srM?分别表示srM的上半球面与下半球面,∑M
r表示srM在ξoη平面上的投影。所以u(x,y,t)=1
2πa2at∫∫∫
at0ΣrMrf(ξ,η,t?)adξdη222r?(ξ?x)?(η?y)r??r2πf(x+ρcosθ,y+ρsinθ,t?1?ρdρdθ?dr=??∫∫2πa2∫r2?ρ20?00?????
在最外一层积分中,作变量置换,令t?r=τ,即r=a(t?τ),dr=?adτ,当r=0时τ=t,当r=at时,τ=0,得a
f(x+ρcosθ,y+ρsinθ,τ)
a2(t?τ)2?ρ2ρdρdθdτ1tu(x,y,t)=2πa∫0
即为所求,与6题结果一致。
8.非齐次方程的柯西问题a(t?τ)2π∫∫00
?utt=?u+2(y?t)?u2?t=0=0,utt=0=x+yz
解:由解的公式得
u(x,y,z,t)=
计算1ψ1ds+∫∫4πaSat4πa2Mr∫∫∫r≤atrf(ξ,η,ζ,t?ar(a=1)
π2πψds=∫∫[(x+rsinθcos?)2+(y+rsinθsin?)(z+rcosθ)]?∫∫r00StM
π2π
?rsinθdθd?2222
r=t=∫∫(x+yz+2xrsinθcos?+rsinθcos?
00
π2ππ2π
+yrcosθ+zrsinθsin?+rsinθcosθsin?)rsinθdθd?
π2π2r=t∫∫sinθdθd?=4π,00∫∫sin002θcos?dθd?=0
∫04sinθcos?dθd?=π,∫3032π2π∫∫sinθcosθdθd?=000
π2π
∫∫sin
002π2πθsin?dθd?=0,∫∫sin002θcosθsin?dθd?=0.
21
所以
StM∫∫rds=4πt(x
r≤tψ24+yz)+πt332(y+rsinθsin??t+r)2rsinθdrdθd?∫∫∫rr≤t计算∫∫∫f(ξ,η,ζ,t?r)dV=r
tπ2π
=2∫∫000∫(y+rsinθsin??t+r)rsinθdrdθd?
tπ
=4π∫∫(y?t+r)rsinθdrdθ
00
所以?1r3?2?=4πyt2?4πt3.=8π?(y?t)r+?23?3??011u(x,y,z,t)=t(x2+yz)+t3+yt2?t3
33
=t(x2+yz+yt)t
即为所求的解。
§5能量不等式,波动方程解的唯一和稳定性
1.设受摩擦力作用的固定端点的有界弦振动,满足方程
utt=a2uxx?cut
证明其能量是减少的,并由此证明方程
utt=a2uxx?cut+f
的混合问题解的唯一性以及关于初始条件及自由项的稳定性。
证:1
能量o首先证明能量是减少。E(t)=∫(ut2+a2ux2)dx
0l
dE(t)=∫(2ututt+2a2uxuxt)dxdt0
l
0l=2∫ututtdx+2a[uxut|?∫utuxxdx]002ll
=2∫ut(utt?a2uxx)dx+2a2uxut|
0ll0
因弦的两端固定,u|x=0=0,u|x=l=0,所以
ut|x=0=0,ut|x=l=0
于是dE(t)=2∫ut(utt?a2uxx)dxdt0
=?2c∫ut2dx<0
0ll(Qc>0)
因此,随着t的增加,E(t)是减少的。
2.证明混合问题解的唯一性
22
混合问题:
?utt=a2uxx?cut+f??u|x=0=0,u|x=l=0
?u|=?(x),u|=ψ(x)tt=0?t=0
设u1,u2是以上问题的解。令u=u1?u2,则u满足
?utt=a2uxx?cut??u|x=0=0,u|x=l=0
?u|=0,u|=0tt=0?t=0
能量2E(t)=∫(ut2+a2ux)dx
0l
当t=0,利用初始条件有ut|t=0=0,由u|t=0=0,得
ux|t=0=0
所以E(0)=0
又E(t)是减少的,故当t>0,E(t)≤E(0)=0,又由E(t)的表达式知E(t)≥0,所以
E(t)≡0
由此得ut≡0,及ux≡0,于是得到
u≡常量
再由初始条件u|t=0=0,得u≡0,因此u1≡u2,即混合问题解的唯一的。
3.证明解关于初始条件的稳定性,即对任何ε.>0,可以找到η>0,只要初始条件之差?1??2,ψ1?ψ2满足
||?1??2||L2<η,||?1x??2x||L2<η,||ψ1?ψ2||L2<η
则始值(?1,ψ1)所对应的解u1及(?2?ψ2)所对应的解u2之差u1?u2满足
||u1?u2||L2<ε
Tl
或∫∫(u1?u2)2dxdt<ε
00
令E0(t)=∫u2(x,t)dx
0l
llldE0(t)2=2∫u?utdx≤∫udx+∫ut2dxdt000
≤E0(t)+E(t)
即d?t(eE0(t)≤e?tE(t)dt
E0(t)≤eE0(0)+e
tttt积分得∫e0?τE(τ)dτt
又E(τ)≤E(0),所以E0(t)≤eE0(0)+eE0(0)∫e?τdτ
0t
23
即E0(t)≤etE0(t)+(et?1)E(0)
记?~=?1??2,ψ~=ψ1?ψ2,则u~=u1?u2满足
??utt=a2uxx?cut
?u|x=0=0,u|x=t=0
??u|t=0=?~,ut|t=0=ψ~
则相对应地有El
0(0)=∫0?~2dx
E(0)=∫(ψ~2+a2?~x2)dx
11l
故若~=??l~2?2
?dx?<η=?L2~
?∫?xL2?~?2
0???2dx?<η
?∫?x
0??
1
~~2
L2=??l?2??∫ψdx?<η0??
则E0(0)<η2,E(0)<(1+a2η)2于是u2L2=E(t)>[et+(et?1)(1+a2220)]η<ε(对任何t)即uL2<ε
11
?Tl
或??∫∫u2dxdt??2
?<η??T
?[et+(et?1)(1+a2)]dt??2<ε/
???∫000??o解关于自由的稳定性
?utt=a2uxx?cut+f1
设ut)满足?
1(x,?u|x=0=0,u|
?x=l=0
?u|t=0=?,ut|t=0=ψ
?utt=a2uxx?cut
ut)满足?+f22(x,?u|x=0=0,u|
?x=l=0
?ut=0=?,ut|t=0=ψ
?utt=a2uxx?cut+(f1?f2)
则u=u?
1?u2满足?u|x=0=0,u|x=l=0
??u|t=0=0,ut|t=0=0
今建立有外力作用时的量不等式(记f=f1?f2)
l
E(t)=∫(ut2+a2ux2)dx
dE(t)l
dt=2∫(ututt+a2uxuxt)dx
l
=2∫ut(utt?a2uxx)dx
l
=2∫(?cut2+utf)dx(Qutt=a2uxx?cut+f)0
24
≤2∫utfdx≤∫utdx+∫f2dx≤E(t)+F(t)
000ll2l
其中F(t)=l
∫f
02dx,故
t
E(t)≤E(0)e+e∫e?tF(τ)dτtt
又E(0)=0
t(由始值),所以t?τE(t)≤e∫eF(τ)dτ=e
0tt∫e0?τdτ∫f2dx0l
≤etTt
∫∫f
002dxdt=K2et
由3o中证明,知
E0(t)≤eE0(0)+ettt
∫e
0?τE(τ)dτ
而E0(0)=0由始值()
t故t?τE0(t)=e∫eE(τ`)dτ≤e
0tt∫K02dτ=tetK2
T
∫E0(t)dt=∫K
00T2tetdt=K2(T?1)eT+1[]
Tl
因此,当K=
l∫∫f2dxdt<η,则002∫∫u0
00dxdt<ηT?1)eT+1<ε
T亦即当∫∫0(f1?f2)0l2dxdt<η,则∫∫0(u1?u2)2dxdt<ε。即解关于自由项是稳定的。
0l
2.证明如果函数f(x,t)在G:0≤x≤l,0≤t≤T作微小改变时,方程?2u
?t2=???u??k(x)??qu+f(x,t)?x??x?
(k(x)>0,q>0和f(x.t)都是一些充分光滑的函数)满足固定端点边界条件的混合问题的解在G内的改变也是很微小的。
?utt=(k(x)ux)x?qu+f?证:只须证明,当f很小时,则问题?u|x=0=0,u|x=l=0的解u也很小(按绝对值)。
?u|=0,u|=0?t=0tt=0
考虑能量E(t)=∫(ut2+k(x)ux2+qu2)dx
0l
dE(t)=∫(2ututt+2k(x)uxuxt+2quut)dxdt0
lll????=2∫ututtdx+?2k(x)uxut|?2∫ut(k(x)ux)xdx?+∫quutdx?0?0?0?0ll
25
由边界条件u|x=0=0,ut|x=l=0,故ut|x=0=0,ul|x=l=0。dE(t)=2∫ut(utt?(k(x)ux)x+qu)dx=2∫ut?f(x,t)dx≤∫ut2dx+∫f2dxdt0000
lllll所以
又由于k(x)>0,q>0,故utdx≤E(t),即
0∫2
dE(t)≤E(t)+∫f2dxdt0
或ld(E(t)e?1)≤e?t∫f2dxdt0
F(t)=∫f2dx
0ll记
得E(t)≤E(0)e+∫et?τF(τ)dτ
0tl
由初始条件u|t=0=0,ut|t=0=0,
l
又因u|t=0=0,得ux|t=0=0,故E(0)=0,即E(t)≤et?τF(τ)dτ∫0
若f很小,即f<η,则f2<η,故
l2F(t)≤∫η2dτ=η2l0l
E(t)≤ηl∫et?τdτ=η2l(et?1)<η2l(eT?1)=ε22
即在[0.T]中任一时刻t,当f很小时,E(t)<ε,又E(t)中积分号下每一项皆为非负的,故
l2
∫k(x)ux
02dx<ε2(对[0,T]中任一时刻t)今对0<x<l,0<t<T,估计u(x,t)。因为?u?u?uu(x,t)?u(0,t)=∫dx≤∫≤∫dx,应用布尼亚科夫斯基不等式,?x?x?x000
lxxl
可以得到∫0?u1dx=∫?x0(x)
2lll???u??2?1k(x)dx≤?∫k(x)dx∫k(x)ux2dx?<Kε?x???00?1其中K=∫k(x)?1dx(因k(x)>0且充分光滑)0l
即
又由边界条件
即当u(x,t)?u(0,t)≤K?εu(0.t)=0,得u(x,t)≤K?ε0<x<l,0<t<T,有u(x,t)很小,得证。
3.证明波动方程
utt=a2(uxx+uyy)+f(x,y,t)
26
的自由项f中在L2(K)意义下作微小改变时,对应的柯西问题的解u在L2(K)意义之下改变也是微小的。R的特征锥Ka证:研究过(x0,y0,
(x?x0)2+(y?y0)2≤(R?at)2
令t=t截K,得截面?t,在?t上研究能量:
E(?t)=∫∫[ut2+a2(ux2+uy2)]dxdy
?t
R?at2πr
=∫∫[ut
002+a2(ux2+uy2)]dsdr(r=(x?x0)2+(y?y0)2)
R?at2πrdE(?t)=2∫∫[ututt+a2(uxuxt+uyuyt)]dsdt?a∫[ut2+a2(ux2+uy2)]dsdt00Γt
其中Γt为?t的边界曲线。再利用奥氏公式,得
R?at2πrdE(?t)=2∫∫ut[utt?a2(uxx+uyy)]dsdtdt00
a??+2∫?a2[uxutcos(n,x)+uyutcos(n,y)]?[ut2+a2(ux2+uy2)]?ds2?Γt?
R?at2πr
=2∫∫utf(x,y,.t)dsdr?a∫[(aux?utcos(n,x))
00?t2+(auy?utcos(n,y))2]ds
因为第二项是非正的,故
dE(t)≤2dt
所以R?at2πr00R?at2πr00∫∫utfdsdr≤∫∫ut2R?at2πrdsdr+∫∫f002dsdrdE(t)≤E(?t)+∫∫f2dxdyd?t?t
令F(t)=∫∫f2dxdy
?t
上式可写成d?t(eE(?t))≤e?tF(t)dt
E(?t)≤E(?0)e+∫et?τF(τ)dτ
0即tt
≤E(?0)e+ettt
∫∫∫f
0?τ2dxdydτ
≤E(?0)et+etRa∫∫∫f
0?τ2dxdydt
即E(?t)≤E(?0)et+et∫∫∫f2dxdydt
K
研究E0(?t)=∫∫u2(x,y,t)dxdy
?t
27
dE0(?t)=2∫∫uu1dxdy?a∫u2dsdt?Γtt
≤2∫∫uu1dxdy≤∫∫u2dxdy+∫∫ut2dxdy
?t?t?t
≤E0(?t)+E(?t)
所以E0(?t)≤E0(?0)e+∫et?τE(?0)dτt
0t
??≤E0(?0)e+∫eE(?0)dτ+∫et?∫∫∫f2dxdydt?dτ??00?K?tttt
=E0(?0)et+tetE(?0)+tet∫∫∫f2dxdydt
K
为证明柯西问题的解的关于自由项的稳定性,只须证明柯西问题
2??utt=auxx+uyy+f(x,y,t)?utt=0=0??ut=0=0,()
??2?当fL2(K)=∫∫∫fdxdydt????K?“很小”时,则解u的模uL2(K)也“很小”此时,由始值utt?0=0,而由于ut=0=0得
ux
所以t=0=0,uyt=0=0E(?0)=0,E0(?0)=0,即
2
L2(K)E0(?t)≤tet∫∫∫f2dxdydt=tetf
K
R
a
u2
L2(K)=∫E0(?t)dt≤f
02L2(K)Ra0∫tedt
2
L2(K)t=f2?
L2(K)??R?aReaR?ea??=M2f??
故任给ε>0,当f2,则u2<<ε得证L(K)L(K)M
4.固定端点有界弦的自由振动可以分解成各种不同固有频率的驻波(谐波)的迭加。试计算各个驻波的动能和位能,并证明弦振动的总能量等于各个驻波能量的迭加。这个物理性质对应的数学事实是什么?解:固定端点有界弦的自由振动,其解为2ε
anπanπ?nπ?u=∑un=∑?Ancost+Bnsint?sinxll?ln=1n=1?
每一个un
l∞∞是一个驻波,将un的总能量记作l22En,位能记作Vn,动能记作Kn,则anπanπ??nπ?nπ?2Vn=∫a2unxdx=a2∫?Ancost+Bnsint??xdx?cos2
llll????00
28
anπanπ?1?anπ??=?t+Bnsint????Ancosll?2?l??
l22
Kn=∫2untdx
0?anπ?=???l?
22lanπanπ?nπ??Ansint+Bncost?sin2xdx∫?lll??022anπanπ?1?anπ??=?t+Bncost?????Ansinll?2?l??
总能量En=Vn+Kn(anπ)22=(A+B2)2lnn
由此知En与t无关,即能量守恒,En(t)=En(0)。
现在计算弦振动的总能量,由于自由振动能量守恒,故总能量E(t)亦满足守恒定律,即
E(t)=∫ut2+a2u2xdx=E(0)
0l()
即E(t)=∫ut2+a2u2x
0l[t=0dx
又由分离变量法,An、Bn由始值决定,且
ut=0=
l∑Ansinn=1∞nπx,utlt=0=∑anπnπBnsinxlln=1∞
所以∫ut
02t=0dx=∫(∑0l∞anπnπanπnπnsinx)?(∑nsinx)dxlllln=1m=1∞
利用?sin?
?nπ?x?在[0,l]上的正交性,得l?
l
∫ut
02∞anπ22(anπ)222nπdx=∫(∑(Bnsinxdx=∑nt=0ll2ln=10n=1l∞
l
同理∫u2x
0?∞nπnπdx=∫?Acos∑n?t=0ll0?n=1
=∑∞l??∞mπmπ?∑x??Acosm??l??m=1l?x??dx?(nπ)2
2l
∞2An∞n=1
所以E(t)=∑(anπ)2(A2+B2)=2lnn
n=1∑E。n=1
l即总能量等于各个驻波能量之和。l2这个物理性质所对应的数学意义说明线性齐次方程在齐次边界知件下,不仅解u具有可加性,而且utdx及u2xdx仍具有可加性。00∫∫
这是由于?sin?
?nπl
2?x?的正交性所决定的。?25.在?∈c,ψ∈c的情况下,证明定理5,即证明此时波动方程柯西问题存在着唯一的广义解,并且它在证理4的意义下是稳定的。证:我们知道当?∈c3,ψ∈c2,则波动方程柯西问题的古典解唯一存在,且在L2(K)意义下关于初始条件使稳定的(定理3、4)今?∈c2,ψ∈c1,根据维尔斯特拉斯定理,存在{?n}∈c3,{ψn}∈c2,当n→∞时?n及其一阶偏导数?nx,?ny分别一致收敛于
29
?,?x及?y,ψn一致收敛于ψ。
记:?n,ψn为初始条件的柯西问题的古典解为un,则un二阶连续可微,且在L2(K)意义下un关于?n,ψn是稳定的。{?n},{ψn}为一致连续序列,自然在L意义下为一基本列,即m,n>N时(?0)(?0:特征锥K与t=0相交截出的圆)2
m??nL2(?0)<η,
L2(?0)mx??nx<η,L2(?0)<η<ηmy??ny
根据{un}的稳定性,得m?ψnL2(?0)
m?unL2(K)=(∫∫∫(um?un)
K2ηdxdydt)2<ε
即{un}在L2(K)意义下为一基本列,根据黎斯—弗歇尔定理,存在唯一的函数u,使当n→∞时
?unL2(K)→0
u即为对应于初始条件?,ψ的柯西问题的广义解。
现在证明广义解的唯一性。若另有?n∈c3,ψn∈c2,当n→∞时n→?,nx→?x,ny→?y且ψn→ψ是一致的,其所对应的古典解un→u(按}}
L2(K)),现在=u,用反证法,若≠u,研究序列
?1,?1,?2,?2,L?n,?n,L
ψ1,1,ψ2,2,Lψn,n,L(1)(2)
则序列(1)及其对x和y的偏导数仍分别一致收敛于?,?x,?y,序列(2)仍为一致收敛于ψ,利用古典解关于初始条件的稳定性,序列
(1)(2)所对应的古典解序列
u1,1,u2,2,L,un,n,L
根据黎期弗歇尔定理,按L2(L)意义收敛于唯一的极限函数。与≠u矛盾。故以上所定义的广义解是唯一的。
若?1∈c2,ψ1∈c1,所对应的广义解记作u1又?2∈c2,ψ2∈c1所对应的广义解记作u2,即存在{?1n}∈c3,{ψ1n}∈c2,{?2n}∈c3,{ψ2n}∈c2。分别一致收敛于?1x,?1y,?2x,?2y则?1n,ψ1n,所对应的古典解u1按L2(K)意义收敛于u1?2n,ψ2n所对应的古典解u2n按L2(K)意义收敛于u2u1?u22L2=∫∫∫(u1?u2)
K2dxdydt
=∫∫∫[(u1?u1n)+(u1n?u2n)+(u2n?u2)]
K2dxdydt
=∫∫∫[(u1?u1n)2+(u1n?u2n)2+(u2n?u2)2+2(u1?u1n)(u1n?u2n)
K
+2(u1_?u1n)(u2n?u2)+2(u1n?u2n)(u2n?u2)]dxdydt
≤3∫∫∫[(u1?u1n)2+(u1n?u2n)2+(u2n?u2)2]dxdydt
K
30
=3[1?u1n22L+u1n?u2n22L+u2n?u222L](3)若1??22<ε,1x??2xL2(?)<ε,1y??2y2<ε,1?ψ2L2(?)<ε。则L(?0)L(?0)00
1n??2nL2(?0)=
?0∫∫(?1n??2n)2dxdy
=
?0∫∫[(?1n??1)+(?1??2)+(?2??2n)]2dxdy
≤3∫∫[(?1n??1)2+(?1??2)2+(?2??2n)2]dxdy
?0
=3[1n??12L2(?0)+1??22L2(?0)+2??2n2L2(?0)]
因?1n→?1,?2n→?2,故当n>N有1n??12<ε,2n??2L2(?)<εL(?0)0
所以1n??2n
同理有2L2(?0)2<9ε即1n??2nL2(?0)<3εL2(?0)1nx??2nxL2(?0)<3ε,1ny??2ny<3ε,1n?ψ2nL2(?0)<3ε
由古典解的稳定性,得u1n?u2n2(当n>N)又由广义解的定义知,对ε′>0,<ε′。L(K)
当n>N′有
u1?u1nL2(K)<ε′,u2?u2nL2(K)<ε′
故当n>max(N,N′)时,由(3)式有
u1?u2
即广义解对于初始条件是稳定的。L2(K)<3ε′
6.对弦振动方程的柯西问题建立广义解的定义,并证明在?(x)为连续,ψ(x)为可积的情形,广义解仍然可以用达朗贝尔公式来给出,因而是连续函数。
解:由达朗贝尔公式知,当?(x)∈c2,ψ(x)∈c1时则柯西问题2??utt=auxx???ut=0=?(x),utt=0=ψ(x)
有古典解u∈c2.且u关于?,ψ是稳定的。
现在按以下方法来定义广义解。
给出一对初始函数e=(?,ψ),?∈c,ψ∈c可以唯的确定一个u。函数对e=(?,ψ)的全体构成一个空间Φ,它的元素的模按以下方式来定义,记(x,t)的依赖区域为X:x?at≤x′≤c+at,记K为区域:x?at≤
上函数对(?,ψ)的值。今定义21x′≤c+at,0≤t′≤t,则u在K上的值仅依赖于X
Φ=max(L2(X),L2(X))
则Φ构成一个线性赋范空间,其中任意两个元素
e1=(?1,ψ1),e2=(?2,ψ2)
的距离为r(e1,e2)=max(1??2L2(X),1?ψ2L2(X))
L2(K)Φ中任一元素对应一个解u是K中二阶连续可微函数,它的全体也构成一个函数空间,记为ψ,其模定义为,二元素u1,u2的距
31
离为1?u22则(?,ψ)与u的关系可以看成Φ到ψ的一个映象,且根据u关于(?,ψ)的稳定性知,映象是连续的。L(K)
现将Φ完备化,考虑Φ中任一基本列{e}={?n,ψn},满足r(en,em)→0,则{?n},{ψn}在X中按L2(X)模成为基本列,由黎斯—弗歇尔定理,存在着极限元素e={?n,ψn}即n??2→0,n?ψL2(X)→0将e添入Φ且定义e={?n,ψn}的模为L(X)eΦ=limenn→∞Φ
则Φ为一完备空间
又{en}为基本列,则所对应的{un}也是一个L(K)中的基本列(稳定性),再根据黎斯—弗歇尔定理,存在着唯一的极限元素2u∈L2(K),u就称为对应于初始条件e={?n,ψn}的弦振动方程柯西问题的广义解。
若?(x)连续,则存在?n(x)∈c2且?n(x)一致收敛于?(x),又ψ(x)可积则必L可积,因此对任意的ε>0存在连续函数ψ0(x),使得
X∫(x)?ψ0(x)dx<ε
0又∫ψ(x)dx?∫ψ
XX(x)≤∫(x)?ψ0(x)<εX
再由维尔斯特拉斯定理知存在ψn(x)∈c1,当n→∞时一致收敛于ψ0(x),即任给ε′>0,当n>N(ε′)时
n(x)?ψ0(x)<ε
于是
X∫n(x)?ψ(x)dx≤∫n(x)?ψ0(x)+∫0(x)?ψ(x)dxXX
<ε′?M+ε=ε′′
当n>N(ε′)
即当n>N(ε′′)时
X∫ψn(x)dx?∫ψ(x)dx<∫n(x)?ψ(x)<εXX
亦即?n(x)dx收敛于?(x)dx。∫X∫X
对于?n(x)∈c,?n(x)∈c,由达朗贝尔公式得,21
11un(x,t)=(?n(x+at)+?n(x?at))+∫?n(α)dα22ax?at
令n→∞,由于?n→?,?n(?)d?=
Xx+atx?atx+at∫∫?n(α)dα→x+atx?at∫?(α)dα,则u(x,t)是收敛的,记其极限函数为u(x,t),得广义解:n
11u(x,t)=(?(x+at)+?(x?at))+22a
又?(x)连续。?(x)可积,则x+at
x?atx+atx?at∫?(α)dα∫?(α)dα也连续,故u(x,t)为连续函数。即得所证。
32
-
数学物理方程小结
数学物理方程小结第七章数学物理定解问题数学物理定解问题包含两个部分数学物理方程即泛定方程和定解条件71数学物理方程的导出一般方法第…
-
0 数学物理方程概述
数学物理方程概述什么是数学物理方程或数学物理方程是研究什么的关于方程含有未知数的等式叫做方程方程有多种多样例如函数方程含有未知函数…
-
数学物理方程期末考试试题及答案
一求解方程15分数学物理方程期末考试试题及答案utta2uxx0uxat0xuxat0x其中00解设xat则方程变为xatu0uF…
-
数学物理方法总结(改)
数学物理方法总结第一章复变函数复数的代数式zxiy复数的三角式和指数式zcossin和zei1izeeiz2i欧拉公式1izcos…
-
数学物理方法大总结
数学物理方法一填空题1函数为0ettx1dtx0又称为第二类欧拉积分的为zettz1dtRez002B函10数又称为第一类欧拉积分…
-
数学物理方法总结(改)
数学物理方法总结第一章复变函数复数的代数式zxiy复数的三角式和指数式zcossin和zei1izeeiz2i欧拉公式1izcos…
-
数学物理方法大总结
数学物理方法一填空题1函数为0ettx1dtx0又称为第二类欧拉积分的为zettz1dtRez002B函10数又称为第一类欧拉积分…
-
数学物理方程小结
数学物理方程小结第七章数学物理定解问题数学物理定解问题包含两个部分数学物理方程即泛定方程和定解条件71数学物理方程的导出一般方法第…
-
数学物理方程读书报告
数学物理方程读书报告遥感与数字地球研究所徐焕20xx28007010031数学物理方程这门课主要是为非数学专业理工科研究生的公共选…
-
0 数学物理方程概述
数学物理方程概述什么是数学物理方程或数学物理方程是研究什么的关于方程含有未知数的等式叫做方程方程有多种多样例如函数方程含有未知函数…