高中数学  选修2－3知识点

第一章   计数原理

知识点：

1、分类加法计数原理：做一件事情，完成它有N类办法，在第一类办法中有M₁种不同的方法，在第二类办法中有M₂种不同的方法，……，在第N类办法中有M_N种不同的方法，那么完成这件事情共有M₁+M₂+……+M_N种不同的方法。

2、分步乘法计数原理：做一件事，完成它需要分成N个步骤，做第一 步有m1种不同的方法，做第二步有M₂不同的方法，……，做第N步有M_N不同的方法.那么完成这件事共有 N=M₁M₂...M_N 种不同的方法。

3、排列：从n个不同的元素中任取m(m≤n)个元素，按照一定顺序排成一列，叫做从n个不同元素中取出m个元素的一个排列

4、排列数：

5、组合：从n个不同的元素中任取m(m≤n)个元素并成一组，叫做从n个不同元素中取出m个元素的一个组合。

6、组合数： 

                          

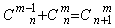
7、二项式定理：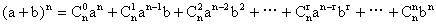

8、二项式通项公式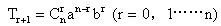

第二章随机变量及其分布

知识点：

1、随机变量：如果随机试验可能出现的结果可以用一个变量X来表示，并且X是随着试验的结果的不同而变化，那么这样的变量叫做随机变量． 随机变量常用大写字母X、Y等或希腊字母 ξ、η等表示。

2、离散型随机变量：在上面的射击、产品检验等例子中，对于随机变量X可能取的值，我们可以按一定次序一一列出，这样的随机变量叫做离散型随机变量．

3、离散型随机变量的分布列：一般的,设离散型随机变量X可能取的值为x₁,x₂,..... ,x_i ,......,x_n

 X取每一个值 x_i(i=1,2,......）的概率P(ξ=x_i）＝P_i，则称表为离散型随机变量X 的概率分布，简称分布列

4、分布列性质① p_i≥0, i =1，2， … 　；② p₁ + p₂ +…+p_n= 1．

5、二点分布：如果随机变量X的分布列为：

其中0<p<1，q=1-p，则称离散型随机变量X服从参数p的二点分布

6、超几何分布：一般地, 设总数为N件的两类物品，其中一类有M件，从所有物品中任取n(n≤N)件,这n件中所含这类物品件数X是一个离散型随机变量，

则它取值为k时的概率为，

其中,且

7、条件概率：对任意事件A和事件B，在已知事件A发生的条件下事件B发生的概率，叫做条件概率.记作P(B|A)，读作A发生的条件下B的概率

8、公式：

    

9、相互独立事件：事件A(或B)是否发生对事件B(或A)发生的概率没有影响,这样的两个事件叫做相互独立事件。

10、n次独立重复事件：在同等条件下进行的，各次之间相互独立的一种试验

11、二项分布： 设在n次独立重复试验中某个事件A发生的次数，A发生次数ξ是一个随机变量．如果在一次试验中某事件发生的概率是p，事件A不发生的概率为q=1-p，那么在n次独立重复试验中 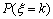（其中 k=0,1, ……,n，q=1-p ）

于是可得随机变量ξ的概率分布如下：

这样的随机变量ξ服从二项分布，记作ξ～B(n，p) ，其中n，p为参数

12、数学期望：一般地，若离散型随机变量ξ的概率分布为

则称 Eξ＝x1p1＋x2p2＋…＋xnpn＋… 为ξ的数学期望或平均数、均值，数学期望又简称为期望．是离散型随机变量。

13、方差:D(ξ)=(x₁-Eξ)²·P₁+（x₂-Eξ)²·P₂ +......+（x_n-Eξ)²·P_n 叫随机变量ξ的均方差，简称方差。

14、集中分布的期望与方差一览：

15、正态分布：

若概率密度曲线就是或近似地是函数

   

的图像，其中解析式中的实数是参数，分别表示总体的平均数与标准差．

则其分布叫正态分布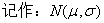，f( x )的图象称为正态曲线。   

16、基本性质：

①曲线在x轴的上方，与x轴不相交．

②曲线关于直线x=对称，且在x=时位于最高点.

③当时，曲线上升；当时，曲线下降．并且当曲线向左、右两边无限延伸时，以x轴为渐近线，向它无限靠近．

④当一定时，曲线的形状由确定．越大，曲线越“矮胖”，表示总体的分布越分散；越小，曲线越“瘦高”，表示总体的分布越集中．

⑤当σ相同时,正态分布曲线的位置由期望值μ来决定.

⑥正态曲线下的总面积等于1.

17、  3原则：

从上表看到,正态总体在   以外取值的概率 只有4.6%,在 以外取值的概率只有0.3%  由于这些概率很小,通常称这些情况发生为小概率事件.也就是说,通常认为这些情况在一次试验中几乎是不可能发生的.

1．某项考试按科目、科目依次进行，只有当科目成绩合格时，才可以继续参加科目 的考试。每个科目只允许有一次补考机会，两个科目成绩均合格方可获得该项合格证书，现在某同学将要参加这项考试，已知他每次考科目成绩合格的概率均为，每次考科目成绩合格的概率均为。假设他在这项考试中不放弃所有的考试机会，且每次的考试成绩互不影响，记他参加考试的次数为。

   (1)求的分布列和均值；

(2)求该同学在这项考试中获得合格证书的概率。

2.济南市有大明湖、趵突泉、千佛山、园博园4个旅游景点，一位客人浏览这四个景点的概率分别是0.3，0.4，0.5，0.6，且客人是否游览哪个景点互不影响，设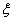表示客人离开该城市时游览的景点数与没有游览的景点数之差的绝对值。

   （1）求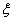=0对应的事件的概率；   （2）求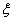的分布列及数学期望。

3. 袋子中装有8个黑球，2个红球，这些球只有颜色上的区别。

（1）随机从中取出2个球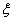，表示其中红球的个数，求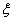的分布列及均值。

（2）现在规定一种有奖摸球游戏如下：每次取球一个，取后不放回，取到黑球有奖，第一个奖100元，第二个奖200元，…，第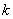个奖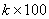元，取到红球则要罚去前期所有奖金并结束取球，按照这种规则，取球多少次比较适宜？说明理由。

第三章统计案例

知识点：

1、独立性检验

假设有两个分类变量X和Y，它们的值域分另为{x₁, x₂}和{y₁, y₂}，其样本频数列联表为： 　　

　若要推断的论述为H₁：“X与Y有关系”，可以利用独立性检验来考察两个变量是否有关系，并且能较精确地给出这种判断的可靠程度。具体的做法是，由表中的数据算出随机变量K^2的值（即K的平方） 　　K² = n (ad - bc) ² / [(a+b)(c+d)(a+c)(b+d)]，其中n=a+b+c+d为样本容量，K²的值越大，说明“X与Y有关系”成立的可能性越大。

  K²≤3.841时，X与Y无关； K²>3.841时，X与Y有95%可能性有关；K²>6.635时X与Y有99%可能性有关

2、回归分析

  回归直线方程  

 其中,     

 

第二篇：【强烈推荐】高中数学知识点总结 选修2-3

第一章 计数原理

1.1 分类加法计数与分步乘法计数

分类加法计数原理： 完成一件事有两类不同方案，在第1类方案中有m种不同的方法，在第2类方案中有n种不同的方法，那么完成这件事共有 N=m+n种不同的方法。分类要做到“不重不漏”。

分步乘法计数原理：完成一件事需要两个步骤。做第1步有m种不同的方法，做第2步有n种不同的方法，那么完成这件事共有N=m×n种不同的方法。分步要做到“步骤完整”。

n元集合A={a1，a2?，an}的不同子集有2n个。

1.2 排列与组合

1.2.1 排列

一般地，从n个不同元素中取出m(m≤n)个元素，按照一定的顺序排成一列，叫做从n个不同元素中取出m个元素的一个排列(arrangement)。

从n个不同元素中取出m(m≤n)个元素的所有不同排列的个数叫做从n个不同元素中取出m个元素的排列数，用符号Amn表示。

排列数公式：

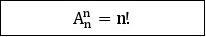
n个元素的全排列数

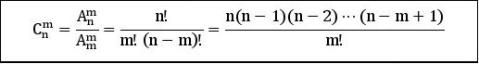
规定：0!=1

1.2.2 组合

一般地，从n个不同元素中取出m(m≤n)个元素合成一组，叫做从n个不同元素中取出m个元素的一个组合(combination)。

从n个不同元素中取出m(m≤n)个元素的所有不同组合的个数，叫做从n个

nm不同元素中取出m个元素的组合数，用符号Cn或 m 表示。

组合数公式：

mm∵ Amn=Cn?Am

∴

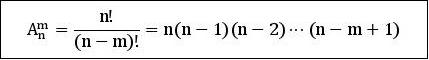
?规定：??=?

组合数的性质：

1.3 二项式定理

1.3.1 二项式定理(binomial theorem)

*注意二项展开式某一项的系数与这一项的二项式系数是两个不同的概念。

1.3.2 “杨辉三角”与二项式系数的性质

*表现形式的变化有时能帮助我们发现某些规律！

(1) 对称性

(2) 当n是偶数时，共有奇数项，中间的一项Cnn+12取得最大值；

n+1

当n是奇数时，共有偶数项，中间的两项Cn，Cn同时取得最大值。

(3) 各二项式系数的和为

012kn 2n=Cn+Cn+Cn+?+Cn+?+Cn

(4) 二项式展开式中，奇数项二项式系数之和等于偶数项二项式系数之和：

024135Cn+Cn+Cn+?=Cn+Cn+Cn+? n?1

(5) 一般地，

rrrrr+1Cr+Cr+1+Cr+2+?+Cn?1=Cn (n>?)

第二章 随机变量及其分布

2.1 离散型随机变量及其分布

2.1.1 离散型随机变量

随着试验结果变化而变化的变量称为随机变量(random variable)。

随机变量和函数都是一种映射，随机变量把随机试验的结果映为实数，函数把实数映为实数。试验结果的范围相当于函数的定义域，随机变量的取值范围相当于函数的值域。

所有取值可以一一列出的随机变量，称为离散型随机变量(discrete random variable)。

概率分布列(probability distribution series)，简称为分布列(distribution series)。

也可用等式表示：

P X=xi =pi ，i=1，2，?，n 根据概率的性质，离散型随机变量的分布列具有如下性质：

(1) pi≥0，i=1，2，?，n；

(2) ni=1pi=1

随机变量X的均值(mean)或数学期望(mathematical expectation)：

E X =x1p1+x2p2+?+xipi+?xnpn

它反映了离散型随机变量取值的平均水平。

随机变量X的方差(variance)刻画了随机变量X与其均值E(X)的平均偏离程度

n

D X = (xi?E(X))2pi

i=1

其算术平方根 D(X)为随机变量X的标准差(standard deviation)。

E aX+b =aE X +b

D aX+b =a2D X

若随机变量X的分布具有下表的形式，则称X服从两点分布(two-point distribution)，并称p=P(X=1)为成功概率。(两点分布又称0-1分布。由于只有两个可能结果的随机试验叫伯努利试验，所以两点分布又叫伯努利分布)

若X

一般地，在含有M件次品的N件产品中，任取n件，其中恰有X件次品，则

? ?=k =

n?kCkMCN?MCN ，k=0，1，2，?，m

如果随机变量X的分布列具有上表的形式，则称随机变量X服从超几何分布(hypergeometric distribution)。

2.2 二项分布及其应用

2.2.1 条件概率

一般地，设A，B为两个事件，且P(A)>0，称

P(AB)P B A = 为在事件A发生的条件下，事件B发生的条件概率(conditional probability)。 如果B和C是两个互斥事件，则

P B∪C A =P B A +P(C|A)

2.2.2 事件的相互独立性

设A，B为两个事件，若

P(AB)=P(A)P(B)

则称事件A与事件B相互独立(mutually independent)。

， 与B， 与? 也都相互独立。 可以证明，如果事件A与B相互独立，那么A与???

2.2.3 独立重复试验与二项分布

一般地，在相同条件下重复做的n次试验称为n次独立重复试验(independent and repeated trials)。

P A1A2?An =P A1 P(A2)?P(An)

其中Ai (i=1，2，?，n)是第i次试验的结果。

一般地，在n次独立重复试验中，用X表示事件A发生的次数，设每次试验中事件A发生的概率为p，则

kkP X=k =Cnp(1?p)n?k ， k=0，1，2，?，n

此时称随机变量X服从二项分布(binomial distribution)，记作X~B(n，p)，并称p为成功概率。

若X~B(n，p) ，则

nnn?1

k?1k?1n?1?(k?1)kkkn?kkn?1?kE X = kCnpq= npCnq=np Cn?1p?1pq

k=0

=np(p+q)k=1

n?1k=0=np

D(X)=np(1?p)

*随机变量的均值是常数，而样本的平均值是随着样本的不同而变化的，因此样本的平均值是随机变量。

随机变量的方差是常数，而样本的方差是随着样本的不同而变化的，因此样本的方差是随机变量。

2.4 正态分布

一般地，如果对于任何实数a，b (a<b)，随机变量X满足

φμ，σ x =1e(x?μ)2?2σ ，x∈（?∞，+∞）

b

a

则称随机变量X服从正态分布(normal distribution)。正态分布完全由参数μ和σ确定，记作N(μ，σ2)。如果随机变量X服从正态分布，则记为X~ N(μ，σ2). P a<?≤? = φμ，σ(x)dx φμ，σ(x)的图像称为正态分布密度曲线，简称正态曲线。

(参数μ是反映随机变量取值的平均水平的特征数，可用样本的均值去估计；σ是衡量随机变量总体波动大小的特征数，可用样本的标准差去估计。)

标准正态分布：X~N(0，1)

经验表明，一个随机变量如果是众多的、互不相干的、不分主次的偶然因素作用结果之和，它就服从或近似服从正态分布。

正态曲线的特点：

(1) 曲线位于x轴上方，与x轴不相交；

(2) 曲线是单峰的，它关于直线x= μ对称；

(3) 曲线在x=μ；

(4) 曲线与x轴之间的面积为1。

*σ越小，曲线越“高瘦”，表示总体分布越集中；σ越大，曲线越“矮胖”，表示总体分布越分散；

若X~ N(μ，σ2)，则对于任何实数a>0，

P μ?a<?≤?+? = μ+a

μ?aφμ，σ(x)dx

该面积随着σ的减少而变大。这说明σ越小，X落在区间(μ?a，μ+a]的概率越大，即X集中在μ周围概率越大。

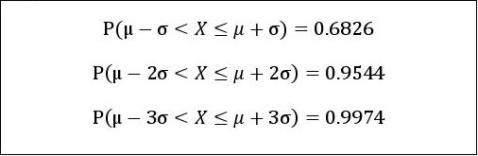
在实际应用中，通常认为服从于正态分布N(μ，σ2)的随机变量X只取 μ?3σ<?≤?+3σ 之间的值，并简称之为??原则。

第三章 统计案例

3.1 回归分析的基本思想

回归分析(regression analysis)是对具有相关关系的两个变量进行统计分析的一种常用方法。

对于一组具有线性相关关系的数据 x1，y1 ， x2，y2 ，?，(xn，yn)

其中x =1

n =b n )(yi?y )(xi?x (x?x)ii=1= n y xiyi?nx x?nxi=1i xa =y ?b n = n ，y )称为样本点的中心，回归直线过样i=1xi ，yi=1yi ，(xn1

本点的中心。

线性回归模型：

y=bx+a+e 2E e =0，D e =σ

其中a和b为模型的未知参数，e是y与bx+a之间的误差。通常e为随机变量，称为随机误差(random error)。 x+a 回归方程：y =b

与函数关系不同，在回归模型中，y的值由x和随机因素e共同确定，即x只能解释部分y的变化，因此我们把x称为解释变量，把y称为预报变量。

随机误差e的方差σ2越小，用bx+a预报真实值y的精度越高。随机误差是引起预报值? 与真实值y之间存在误差的原因之一，其大小取决于随机误差的方差。

和a另一方面，b 为斜率和截距的估计值，它们与真实值a和b之间也存在误差，这种误差是引起预报值y 与真实值y之间存在误差的另一个原因。

由于随机误差 e=y?(bx+a)，所以e =y?y 是e的估计量。

对于样本点

x1，y1 ， x2，y2 ，?，(xn，yn)

它们的随机误差为

ei=yi?bxi?a，i=1，2，?，n

其估计值为

xi?ae i=yi?y i=yi?b ，i=1，2，?，n

e i称为相应于点 xi，yi 的残差(residual)。

可以通过残差发现原始数据中的可疑数据，判断所建立模型的拟合效果。 以样本编号为横坐标，残差为纵坐标，可作出残差图。

检查残差较大的样本点，确认采集该样本点过程中是否有人为错误，如有，应予以纠正，再重新利用线性回归模型拟合数据；如没有，则需寻找其它原因。

另外，对于已经获取的样本数据，

n i)2i=1(yi?yR=1?i=1i2

中的 n )2为确定的数。因此R2越大，意味着残差平方和 n i)2越i=1(yi?yi=1(yi?y小，即模型拟合效果越好；R2越小，残差平方和越大，即模型拟合效果越差。 R2表示解释变量对于预报变量变化的贡献率，R2越接近于1，表示回归的效果越好。

一般地，建立回归模型的基本步骤：

(1) 确定研究对象，明确哪个变量是解释变量，哪个变量是预报变量；

(2) 画出解释变量和预报变量的散点图，观察它们之间的关系(如是否存在线性关系等)

(3) 有经验确定回归方程的类型(如我们观察到数据呈线性关系，则选用线性回归方程)

(4) 按一定规则(如最小二乘法)估计回归方程中的参数；

(5) 得出结果后分析残差图是否有异常(如个别数据对应残差过大，残差呈现不随

机的规律性等)。若存在异常，则检查数据是否有误，或模型是否合适等。

回归模型的适用范围：

(1) 回归方程只适用于我们所研究的样本的总体；

(2) 我们所建立的回归方程一般都有时间性；

(3) 样本取值的范围会影响回归方程的适用范围；

(4) 不能期望回归方程得到的预报值就是预报变量的精确值。

一般地，比较两个函数模型的拟合程度的步骤如下：

(1) 分别建立对应于两个模型的回归方程y )与y 其中a 和b1=f(x，a2=g(x，b) ，

分别是参数a和b的估计值

(2) 分别计算两个模型的R2值

222(3) 若R21>R2 ，则模型1比模型2拟合效果更好；若R1<R2 ，则模型2比模

型1拟合效果更好。

3.2 独立性检验的基本思想

不同的“值”表示不同类别的变量叫做分类变量。列出两个分类变量的频数表称为列联表(contingency table)。常用等高条形图展示列联表数据的频率特征。

利用随机变量K2来判断“两个分类变量有关系”的方法称为独立性检验(test of independence)。

一般地，假设有两个分类变量X和Y，它们的取值分别为{x1，x2}和{y1，y2}，其

则有P(XY)=P(X)P(Y) ；

根据频率近似于概率，故有

aa+ba+c≈× 化简得 ad≈bc

因此，|ad?bc|越小，两者关系越弱；|ad?bc|越大，两者关系越强； 基于以上分析，构造随机变量

K=2n(ad?bc)2

，其中n=a+b+c+d为样本容量 a+b c+d a+c (b+d)

K2的值越小则关系越小，K2的值越大则关系越大。(实际应用中通常要求a，b，c，d都不小于5)

计算K2的观测值k并与K2作比较。

统计学研究发现，在H0成立的情况下，

P K2≥6.635 =0.01

即在H0成立的情况下，K2的观测值超过6.635的概率非常小，近似为0.01，是一个小概率事件。

若观测值k大于6.635，则有理由判定H0不成立，即“X与Y有关系”。但这种判断会犯错误，犯错误的概率不会超过0.01 .

*(这里概率计算的前提是H0成立，即H0：两个分类变量没有关系)

若要推断的论述为H1：“X与Y有关系”。可以通过频率直观地判断两个条件概率P(Y=y1|X=x1)和P(Y=y1|X=x2)是否相等。如果判断它们相等，就意味着X和Y没有

a关系；否则就认为它们有关系。由上表可知，在X=x1的情况下，Y=y1的频率为 ；a+b

c在X=x2的情况下，Y=y1的频率为 。因此，如果通过直接计算或等高条形图c+d

ac发现 a+bc+d

利用独立性检验原理可以进一步给出推断“两个分类变量有关系”犯错误的概率。具体做法是：

(1) 根据实际问题的需要确定容许推断“两个分类变量有关系”犯错误概率的上

(2) 利用公式计算随机变量K2的观测值k.

(3) 如果K2的观测值k大于判断规则的临界值k0，即k≥k0，就推断“X与Y有关

系”，这种推断犯错误的概率不超过α ；否则，就认为在犯错误的概率不超过α的前提下不能推断“X与Y有关系”，或者在样本数据中没有发现足够证据支持结论“X与Y有关系”。

按照上述规则，把“两个分类变量之间没有关系”错误地判断为“两个分类变量

之间有关系”的概率不超过P K2≥k0 .

定义：

acW= ?

则

n a+b (c+d)22K=W× 若“X和Y没有关系”则有

P K2≥k0 =0.01

有K2≥k0可推出

W≥ k0×

即可取

a+c (b+d)w0= k0× 于是有以下判断规则： 当W的观测值w>w0时，就判断“X和Y有关系” ；否则，判断“X和Y没有关系”。这里w0为正实数，且满足在“X和Y没有关系”的前提下

P W2≥w0 =0.01

a+c (b+d)