东北大学数值分析实验报告
数值分析实验
班级 姓名 学号
实验环境：MATLAB
实验一 解线性方程组的迭代法
一、实验题目 对以下方程组分别采用Jacobi迭代法，Gaaus-Seidel迭代法求解和SOR迭代法求解。
（1）线性方程组
=
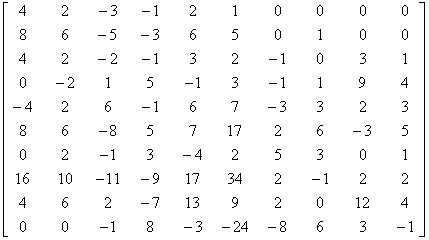
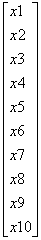（2）对称正定线性方程组
=
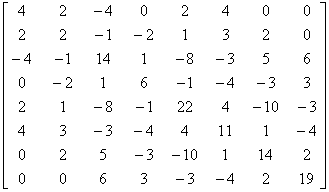
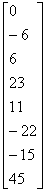
（3）三对角线性方程组
=
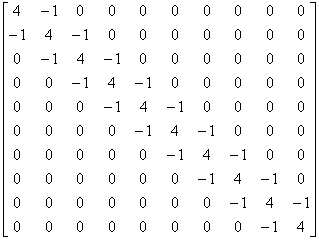
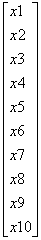二、实验要求
（1）应用迭代法求线性方程组，并与直接法作比较。
（2）分别对不同精度要求，如ε=
，
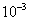，利用所需迭代次数体会改迭代法的收敛快慢。
（3）对方程组使用SOR方法时，选取松弛因子ω=0.8,0.9,1,1.1,1,1.2等，试观察对算法收敛性的影响，并找出你所选的松弛因子的最佳值。
（4）编制出各种迭代法的程序并给出计算结果。
三、源程序及实验结果
Jacobi迭代法函数为
function[x,k]=Jacobi(A,b,x0,wc)
n=length(b);k=0;x=x0;
while max(abs(b-A*x0))>wc&k<=500
for i=1:n
sum=0;
for j=1:n
if j~=i
sum=sum+A(i,j)*x0(j)[1]
end
end
x(i)=(b(i)-sum)/A(i,i);
end
x0=x;k=k+1;
if k>500
fprintf('µü´ú´ïµ½ÉÏÏÞ')
return
end
end
Gauss-Seidel迭代法函数为
function[x,k]=Gaussseidel(A,b,x,wc,N)
n=length(b);k=0;
while max(abs(b-A*x))>wc&k<=N
for i=1:n
sum=0;
for j=1:n
if j~=i
sum=sum+A(i,j)*x(j)
end
end
x(i)=(b(i)-sum)/A(i,i);
end
k=k+1;
if k>=N
fprintf('?ü?ú????????')
return
end
end
SOR迭代法的函数
function[x,k]=SOR(A,b,x0,emg,N,w)
n=length(b);
x=zeros(n,1);
r=max(abs(b-A*x0));
k=0;
while (r>emg)&(k<N)
for i=1:n
sum=0;
for j=1:n
if j>i
sum=sum+A(i,j)*x0(j);
elseif j<i
sum=sum+A(i,j)*x(j);
end
end
x(i)=(1-w)*x0(i)+w(b(i)-sum)/A(i,i);
end
r=max(abs(x-x0));
x0=x;k=k+1;
if k>=N
warning('迭代次数达到上限！');
return
end
end
方程组一
直接求解法
>> A=[4 2 -3 -1 2 1 0 0 0 0;8 6 -5 -3 6 5 0 1 0 0;4 2 -2 -1 3 2 -1 0 3 1;0 -2 1 5 -1 3 -1 1 9 4;-4 2 6 -1 6 7 -3 3 2 3;8 6 -8 5 7 17 2 6 -3 5;0 2 -1 3 -4 2 5 3 0 1;16 10 -11 -9 17 34 2 -1 2 2;4 6 2 -7 13 9 2 0 12 4;0 0 -1 8 -3 -24 -8 6 3 -1 ];
b=[5 12 3 2 3 46 13 38 19 -21]';
>> x=inv(A)*b
运行结果
x =
1.0000
-1.0000
-0.0000
1.0000
2.0000
-0.0000
3.0000
1.0000
-1.0000
2.0000
Jacobi方法
（1）精度为
时
（2）A=[4 2 -3 -1 2 1 0 0 0 0;8 6 -5 -3 6 5 0 1 0 0;4 2 -2 -1 3 2 -1 0 3 1;0 -2 1 5 -1 3 -1 1 9 4;-4 2 6 -1 6 7 -3 3 2 3;8 6 -8 5 7 17 2 6 -3 5;0 2 -1 3 -4 2 5 3 0 1;16 10 -11 -9 17 34 2 -1 2 2;4 6 2 -7 13 9 2 0 12 4;0 0 -1 8 -3 -24 -8 6 3 -1 ];
b=[5 12 3 2 3 46 13 38 19 -21]';
x0=[0 0 0 0 0 0 0 0 0 0]';
[x,k]=Jacobi(A,b,x0,1e-3)
运行结果
x =
1.0e+307 *
-0.6183
-1.2682
-1.9643
Inf
Inf
NaN
0.0572
Inf
Inf
0.0575
k =
495
（2）精度为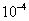
时
>> A=[4 2 -3 -1 2 1 0 0 0 0;8 6 -5 -3 6 5 0 1 0 0;4 2 -2 -1 3 2 -1 0 3 1;0 -2 1 5 -1 3 -1 1 9 4;-4 2 6 -1 6 7 -3 3 2 3;8 6 -8 5 7 17 2 6 -3 5;0 2 -1 3 -4 2 5 3 0 1;16 10 -11 -9 17 34 2 -1 2 2;4 6 2 -7 13 9 2 0 12 4;0 0 -1 8 -3 -24 -8 6 3 -1 ];
b=[5 12 3 2 3 46 13 38 19 -21]';
x0=[0 0 0 0 0 0 0 0 0 0]';
[x,k]=Jacobi(A,b,x0,1e-4)
运行结果
x =
1.0e+307 *
-0.6183
-1.2682
-1.9643
Inf
Inf
NaN
0.0572
Inf
Inf
0.0575
k =
495
（3）精度为
时
>> A=[4 2 -3 -1 2 1 0 0 0 0;8 6 -5 -3 6 5 0 1 0 0;4 2 -2 -1 3 2 -1 0 3 1;0 -2 1 5 -1 3 -1 1 9 4;-4 2 6 -1 6 7 -3 3 2 3;8 6 -8 5 7 17 2 6 -3 5;0 2 -1 3 -4 2 5 3 0 1;16 10 -11 -9 17 34 2 -1 2 2;4 6 2 -7 13 9 2 0 12 4;0 0 -1 8 -3 -24 -8 6 3 -1 ];
b=[5 12 3 2 3 46 13 38 19 -21]';
x0=[0 0 0 0 0 0 0 0 0 0]';
[x,k]=Jacobi(A,b,x0,1e-5)
运行结果
x =
1.0e+307 *
-0.6183
-1.2682
-1.9643
Inf
Inf
NaN
0.0572
Inf
Inf
0.0575
k =
495
结论 由以上实验结果可知该方程组不能使用Jacobi迭代法求解。
Gauss-Seidel迭代法
（1）精度为时
>> A=[4 2 -3 -1 2 1 0 0 0 0;8 6 -5 -3 6 5 0 1 0 0;4 2 -2 -1 3 2 -1 0 3 1;0 -2 1 5 -1 3 -1 1 9 4;-4 2 6 -1 6 7 -3 3 2 3;8 6 -8 5 7 17 2 6 -3 5;0 2 -1 3 -4 2 5 3 0 1;16 10 -11 -9 17 34 2 -1 2 2;4 6 2 -7 13 9 2 0 12 4;0 0 -1 8 -3 -24 -8 6 3 -1 ];
b=[5 12 3 2 3 46 13 38 19 -21]';
x=[0 0 0 0 0 0 0 0 0 0]';
[x,k]=Gaussseidel(A,b,x,1e-3,500)
实验结果
x =
1.0e+307 *
0.0460
-0.0754
0.6126
-1.2732
-1.6558
Inf
-Inf
NaN
NaN
NaN
k =
249
(2)精度为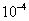时
>> A=[4 2 -3 -1 2 1 0 0 0 0;8 6 -5 -3 6 5 0 1 0 0;4 2 -2 -1 3 2 -1 0 3 1;0 -2 1 5 -1 3 -1 1 9 4;-4 2 6 -1 6 7 -3 3 2 3;8 6 -8 5 7 17 2 6 -3 5;0 2 -1 3 -4 2 5 3 0 1;16 10 -11 -9 17 34 2 -1 2 2;4 6 2 -7 13 9 2 0 12 4;0 0 -1 8 -3 -24 -8 6 3 -1 ];
b=[5 12 3 2 3 46 13 38 19 -21]';
x=[0 0 0 0 0 0 0 0 0 0]';
[x,k]=Gaussseidel(A,b,x,1e-4,500)
实验结果
x =
1.0e+307 *
0.0460
-0.0754
0.6126
-1.2732
-1.6558
Inf
-Inf
NaN
NaN
NaN
k =
249
(3)精度为时
>> A=[4 2 -3 -1 2 1 0 0 0 0;8 6 -5 -3 6 5 0 1 0 0;4 2 -2 -1 3 2 -1 0 3 1;0 -2 1 5 -1 3 -1 1 9 4;-4 2 6 -1 6 7 -3 3 2 3;8 6 -8 5 7 17 2 6 -3 5;0 2 -1 3 -4 2 5 3 0 1;16 10 -11 -9 17 34 2 -1 2 2;4 6 2 -7 13 9 2 0 12 4;0 0 -1 8 -3 -24 -8 6 3 -1 ];
b=[5 12 3 2 3 46 13 38 19 -21]';
x=[0 0 0 0 0 0 0 0 0 0]';
[x,k]=Gaussseidel(A,b,x,1e-5,500)
实验结果
x =
1.0e+307 *
0.0460
-0.0754
0.6126
-1.2732
-1.6558
Inf
-Inf
NaN
NaN
NaN
k =
249
结论 由以上实验结果可知该方程组不能用Gauss-Seidel方法求解。且SOR迭代法是J迭代法或者GS迭代法的改进，所以该方程组一定不能使用SOR迭代法求解。
方程组二
直接法
>> A=[4 2 -4 0 2 4 0 0;2 2 -1 -2 1 3 2 0;-4 -1 14 1 -8 -3 5 6;0 -2 1 6 -1 -4 -3 3;2 1 -8 -1 22 4 -10 -3;4 3 -3 -4 4 11 1 -4;0 2 5 -3 -10 1 14 2;0 0 6 3 -3 -4 2 19];
b=[0 -6 6 23 11 -22 -15 45]';
x=inv(A)*b
运行结果
x =
1.0000
-1.0000
-0.0000
2.0000
1.0000
-1.0000
0.0000
2.0000
Jacobi方法
（1）求解精度为时
>>A=[4 2 -4 0 2 4 0 0;2 2 -1 -2 1 3 2 0;-4 -1 14 1 -8 -3 5 6;0 -2 1 6 -1 -4 -3 3;2 1 -8 -1 22 4 -10 -3;4 3 -3 -4 4 11 1 -4;0 2 5 -3 -10 1 14 2;0 0 6 3 -3 -4 2 19];
b=[0 -6 6 23 11 -22 -15 45]';
x0=[0 0 0 0 0 0 0 0]';
[x,k]=Jacobi(A,b,x0,1e-3)
运行结果
x =
1.0e+144 *
-1.4659
-2.2112
0.6014
0.8769
-0.3575
-0.9590
-0.0305
0.3007
k =
501
(2)精度为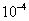时
>>A=[4 2 -4 0 2 4 0 0;2 2 -1 -2 1 3 2 0;-4 -1 14 1 -8 -3 5 6;0 -2 1 6 -1 -4 -3 3;2 1 -8 -1 22 4 -10 -3;4 3 -3 -4 4 11 1 -4;0 2 5 -3 -10 1 14 2;0 0 6 3 -3 -4 2 19];
b=[0 -6 6 23 11 -22 -15 45]';
x0=[0 0 0 0 0 0 0 0]';
[x,k]=Jacobi(A,b,x0,1e-4)
实验结果
x =
1.0e+144 *
-1.4659
-2.2112
0.6014
0.8769
-0.3575
-0.9590
-0.0305
0.3007
k =
501
(3)精度为时
>>A=[4 2 -4 0 2 4 0 0;2 2 -1 -2 1 3 2 0;-4 -1 14 1 -8 -3 5 6;0 -2 1 6 -1 -4 -3 3;2 1 -8 -1 22 4 -10 -3;4 3 -3 -4 4 11 1 -4;0 2 5 -3 -10 1 14 2;0 0 6 3 -3 -4 2 19];
b=[0 -6 6 23 11 -22 -15 45]';
x0=[0 0 0 0 0 0 0 0]';
[x,k]=Jacobi(A,b,x0,1e-5)
实验结果
x =
1.0e+144 *
-1.4659
-2.2112
0.6014
0.8769
-0.3575
-0.9590
-0.0305
0.3007
k =
501
结论 由此结果可知次方程组由Jacobi方法求解时，收敛速度太慢，不能求出较为精确的解。
Gauss-Seidel迭代法
（1）求解精度为时
>>A=[4 2 -4 0 2 4 0 0;2 2 -1 -2 1 3 2 0;-4 -1 14 1 -8 -3 5 6;0 -2 1 6 -1 -4 -3 3;2 1 -8 -1 22 4 -10 -3;4 3 -3 -4 4 11 1 -4;0 2 5 -3 -10 1 14 2;0 0 6 3 -3 -4 2 19];
b=[0 -6 6 23 11 -22 -15 45]';
x=[0 0 0 0 0 0 0 0]';
[x,k]=Gaussseidel(A,b,x,1e-3,500)
运行结果
x =
1.0475
-1.0558
0.0111
1.9753
1.0039
-1.0101
0.0024
1.9986
k =
364
（2）精度为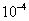时
>>A=[4 2 -4 0 2 4 0 0;2 2 -1 -2 1 3 2 0;-4 -1 14 1 -8 -3 5 6;0 -2 1 6 -1 -4 -3 3;2 1 -8 -1 22 4 -10 -3;4 3 -3 -4 4 11 1 -4;0 2 5 -3 -10 1 14 2;0 0 6 3 -3 -4 2 19];
b=[0 -6 6 23 11 -22 -15 45]';
x=[0 0 0 0 0 0 0 0]';
[x,k]=Gaussseidel(A,b,x,1e-4,500)
实验结果
x =
1.0232
-1.0272
0.0054
1.9880
1.0019
-1.0049
0.0012
1.9993
k =
500
(3)精度为时
>>A=[4 2 -4 0 2 4 0 0;2 2 -1 -2 1 3 2 0;-4 -1 14 1 -8 -3 5 6;0 -2 1 6 -1 -4 -3 3;2 1 -8 -1 22 4 -10 -3;4 3 -3 -4 4 11 1 -4;0 2 5 -3 -10 1 14 2;0 0 6 3 -3 -4 2 19];
b=[0 -6 6 23 11 -22 -15 45]';
x=[0 0 0 0 0 0 0 0]';
[x,k]=Gaussseidel(A,b,x,1e-5,1000)
实验结果
x =
1.0017
-1.0020
0.0004
1.9991
1.0001
-1.0004
0.0001
2.0000
k =
1000
结论 由以上实验结果可知Gauss-Seidel迭代法比Jacobi迭代法具有更好的收敛速度，但是对于此方程组收敛速度还是较慢。
SOR迭代法
(1)
ω=0.8时
?求解精度为时
>>A=[4 2 -4 0 2 4 0 0;2 2 -1 -2 1 3 2 0;-4 -1 14 1 -8 -3 5 6;0 -2 1 6 -1 -4 -3 3;2 1 -8 -1 22 4 -10 -3;4 3 -3 -4 4 11 1 -4;0 2 5 -3 -10 1 14 2;0 0 6 3 -3 -4 2 19];
b=[0 -6 6 23 11 -22 -15 45]';
x0=[0 0 0 0 0 0 0 0]';
[x,k]=SOR(A,b,x0,1e-3,500,0.8)
实验结果
x =
1.1040
-1.1182
0.0254
1.9473
1.0097
-1.0236
0.0059
1.9961
k =
13
?精度为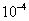时
>>A=[4 2 -4 0 2 4 0 0;2 2 -1 -2 1 3 2 0;-4 -1 14 1 -8 -3 5 6;0 -2 1 6 -1 -4 -3 3;2 1 -8 -1 22 4 -10 -3;4 3 -3 -4 4 11 1 -4;0 2 5 -3 -10 1 14 2;0 0 6 3 -3 -4 2 19];
b=[0 -6 6 23 11 -22 -15 45]';
x0=[0 0 0 0 0 0 0 0]';
[x,k]=SOR(A,b,x0,1e-4,500,0.8)
实验结果
x =
1.0241
-1.0284
0.0057
1.9875
1.0020
-1.0051
0.0012
1.9993
k =
427
?精度为时
>>A=[4 2 -4 0 2 4 0 0;2 2 -1 -2 1 3 2 0;-4 -1 14 1 -8 -3 5 6;0 -2 1 6 -1 -4 -3 3;2 1 -8 -1 22 4 -10 -3;4 3 -3 -4 4 11 1 -4;0 2 5 -3 -10 1 14 2;0 0 6 3 -3 -4 2 19];
b=[0 -6 6 23 11 -22 -15 45]';
x0=[0 0 0 0 0 0 0 0]';
[x,k]=SOR(A,b,x0,1e-5,1000,0.8)
实验结果
x =
1.0032
-1.0038
0.0008
1.9983
1.0003
-1.0007
0.0002
1.9999
k =
1000
(2)ω=0.9时
?求解精度为时
>>A=[4 2 -4 0 2 4 0 0;2 2 -1 -2 1 3 2 0;-4 -1 14 1 -8 -3 5 6;0 -2 1 6 -1 -4 -3 3;2 1 -8 -1 22 4 -10 -3;4 3 -3 -4 4 11 1 -4;0 2 5 -3 -10 1 14 2;0 0 6 3 -3 -4 2 19];
b=[0 -6 6 23 11 -22 -15 45]';
x0=[0 0 0 0 0 0 0 0]';
[x,k]=SOR(A,b,x0,1e-3,500,0.9)
实验结果
x =
1.1940
-1.2270
0.0459
1.8997
1.0164
-1.0418
0.0102
1.9941
k =
14
?精度为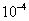时
>>A=[4 2 -4 0 2 4 0 0;2 2 -1 -2 1 3 2 0;-4 -1 14 1 -8 -3 5 6;0 -2 1 6 -1 -4 -3 3;2 1 -8 -1 22 4 -10 -3;4 3 -3 -4 4 11 1 -4;0 2 5 -3 -10 1 14 2;0 0 6 3 -3 -4 2 19];
b=[0 -6 6 23 11 -22 -15 45]';
x0=[0 0 0 0 0 0 0 0]';
[x,k]=SOR(A,b,x0,1e-4,500,0.9)
实验结果
x =
1.0238
-1.0280
0.0056
1.9876
1.0020
-1.0051
0.0012
1.9993
k =
500
?精度为时
>>A=[4 2 -4 0 2 4 0 0;2 2 -1 -2 1 3 2 0;-4 -1 14 1 -8 -3 5 6;0 -2 1 6 -1 -4 -3 3;2 1 -8 -1 22 4 -10 -3;4 3 -3 -4 4 11 1 -4;0 2 5 -3 -10 1 14 2;0 0 6 3 -3 -4 2 19];
b=[0 -6 6 23 11 -22 -15 45]';
x0=[0 0 0 0 0 0 0 0]';
[x,k]=SOR(A,b,x0,1e-5,1000,0.9)
实验结果
x =
1.0028
-1.0032
0.0006
1.9986
1.0002
-1.0006
0.0001
1.9999
k =
1000
(3)ω=1.0时
?求解精度为时
>>A=[4 2 -4 0 2 4 0 0;2 2 -1 -2 1 3 2 0;-4 -1 14 1 -8 -3 5 6;0 -2 1 6 -1 -4 -3 3;2 1 -8 -1 22 4 -10 -3;4 3 -3 -4 4 11 1 -4;0 2 5 -3 -10 1 14 2;0 0 6 3 -3 -4 2 19];
b=[0 -6 6 23 11 -22 -15 45]';
x0=[0 0 0 0 0 0 0 0]';
[x,k]=SOR(A,b,x0,1e-3,1000,1)
实验结果
x =
1.1604
-1.1886
0.0377
1.9166
1.0133
-1.0342
0.0082
1.9953
k =
133
?精度为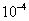时
>>A=[4 2 -4 0 2 4 0 0;2 2 -1 -2 1 3 2 0;-4 -1 14 1 -8 -3 5 6;0 -2 1 6 -1 -4 -3 3;2 1 -8 -1 22 4 -10 -3;4 3 -3 -4 4 11 1 -4;0 2 5 -3 -10 1 14 2;0 0 6 3 -3 -4 2 19];
b=[0 -6 6 23 11 -22 -15 45]';
x0=[0 0 0 0 0 0 0 0]';
[x,k]=SOR(A,b,x0,1e-4,1000,1)
实验结果
x =
1.0160
-1.0188
0.0038
1.9917
1.0013
-1.0034
0.0008
1.9995
k =
570
?精度为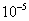
时
>>A=[4 2 -4 0 2 4 0 0;2 2 -1 -2 1 3 2 0;-4 -1 14 1 -8 -3 5 6;0 -2 1 6 -1 -4 -3 3;2 1 -8 -1 22 4 -10 -3;4 3 -3 -4 4 11 1 -4;0 2 5 -3 -10 1 14 2;0 0 6 3 -3 -4 2 19];
b=[0 -6 6 23 11 -22 -15 45]';
x0=[0 0 0 0 0 0 0 0]';
[x,k]=SOR(A,b,x0,1e-5,1000,1)
实验结果
x =
1.0017
-1.0020
0.0004
1.9991
1.0001
-1.0004
0.0001
2.0000
k =
1000
(4)ω=1.1时
?求解精度为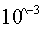
时
>>A=[4 2 -4 0 2 4 0 0;2 2 -1 -2 1 3 2 0;-4 -1 14 1 -8 -3 5 6;0 -2 1 6 -1 -4 -3 3;2 1 -8 -1 22 4 -10 -3;4 3 -3 -4 4 11 1 -4;0 2 5 -3 -10 1 14 2;0 0 6 3 -3 -4 2 19];
b=[0 -6 6 23 11 -22 -15 45]';
x0=[0 0 0 0 0 0 0 0]';
[x,k]=SOR(A,b,x0,1e-3,1000,1.1)
实验结果
x =
1.1314
-1.1543
0.0309
1.9318
1.0109
-1.0281
0.0067
1.9961
k =
197
?精度为
时
>>A=[4 2 -4 0 2 4 0 0;2 2 -1 -2 1 3 2 0;-4 -1 14 1 -8 -3 5 6;0 -2 1 6 -1 -4 -3 3;2 1 -8 -1 22 4 -10 -3;4 3 -3 -4 4 11 1 -4;0 2 5 -3 -10 1 14 2;0 0 6 3 -3 -4 2 19];
b=[0 -6 6 23 11 -22 -15 45]';
x0=[0 0 0 0 0 0 0 0]';
[x,k]=SOR(A,b,x0,1e-4,1000,1.1)
实验结果
x =
1.0131
-1.0154
0.0031
1.9932
1.0011
-1.0028
0.0007
1.9996
k =
554
?精度为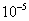时
>>A=[4 2 -4 0 2 4 0 0;2 2 -1 -2 1 3 2 0;-4 -1 14 1 -8 -3 5 6;0 -2 1 6 -1 -4 -3 3;2 1 -8 -1 22 4 -10 -3;4 3 -3 -4 4 11 1 -4;0 2 5 -3 -10 1 14 2;0 0 6 3 -3 -4 2 19];
b=[0 -6 6 23 11 -22 -15 45]';
x0=[0 0 0 0 0 0 0 0]';
[x,k]=SOR(A,b,x0,1e-5,1000,1.1)
实验结果
x =
1.0013
-1.0015
0.0003
1.9993
1.0001
-1.0003
0.0001
2.0000
k =
911
(5)ω=1.2时
?求解精度为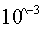时
>>A=[4 2 -4 0 2 4 0 0;2 2 -1 -2 1 3 2 0;-4 -1 14 1 -8 -3 5 6;0 -2 1 6 -1 -4 -3 3;2 1 -8 -1 22 4 -10 -3;4 3 -3 -4 4 11 1 -4;0 2 5 -3 -10 1 14 2;0 0 6 3 -3 -4 2 19];
b=[0 -6 6 23 11 -22 -15 45]';
x0=[0 0 0 0 0 0 0 0]';
[x,k]=SOR(A,b,x0,1e-3,1000,1.2)
实验结果
x =
1.1068
-1.1253
0.0251
1.9446
1.0088
-1.0228
0.0054
1.9968
k =
228
?精度为时
>>A=[4 2 -4 0 2 4 0 0;2 2 -1 -2 1 3 2 0;-4 -1 14 1 -8 -3 5 6;0 -2 1 6 -1 -4 -3 3;2 1 -8 -1 22 4 -10 -3;4 3 -3 -4 4 11 1 -4;0 2 5 -3 -10 1 14 2;0 0 6 3 -3 -4 2 19];
b=[0 -6 6 23 11 -22 -15 45]';
x0=[0 0 0 0 0 0 0 0]';
[x,k]=SOR(A,b,x0,1e-4,1000,1.2)
实验结果
x =
1.0106
-1.0125
0.0025
1.9945
1.0009
-1.0023
0.0005
1.9997
k =
519
?精度为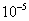时
>>A=[4 2 -4 0 2 4 0 0;2 2 -1 -2 1 3 2 0;-4 -1 14 1 -8 -3 5 6;0 -2 1 6 -1 -4 -3 3;2 1 -8 -1 22 4 -10 -3;4 3 -3 -4 4 11 1 -4;0 2 5 -3 -10 1 14 2;0 0 6 3 -3 -4 2 19];
b=[0 -6 6 23 11 -22 -15 45]';
x0=[0 0 0 0 0 0 0 0]';
[x,k]=SOR(A,b,x0,1e-5,1000,1.2)
实验结果
x =
1.0011
-1.0013
0.0003
1.9994
1.0001
-1.0002
0.0001
2.0000
k =
809
结论 SOR迭代法比Jacobi迭代法和Gauss-seidel迭代法具有更好的收敛速度。且当精度要求不超过
时，松弛因子的最佳值是0.8，当精度要求大于等于
时，松弛因子的最佳值是1.2 。
方程组三
直接求解法
>> A=[4 -1 0 0 0 0 0 0 0 0;-1 4 -1 0 0 0 0 0 0 0;0 -1 4 -1 0 0 0 0 0 0;0 0 -1 4 -1 0 0 0 0 0;0 0 0 -1 4 -1 0 0 0 0;0 0 0 0 -1 4 -1 0 0 0;0 0 0 0 0 -1 4 -1 0 0;0 0 0 0 0 0 -1 4 -1 0;0 0 0 0 0 0 0 -1 4 -1;0 0 0 0 0 0 0 0 -1 4];
b=[7 5 -13 2 6 -12 14 -4 5 -5]';
x0=[0 0 0 0 0 0 0 0 0 0]';
>> x=inv(A)*b
实验结果
x =
2.0000
1.0000
-3.0000
-0.0000
1.0000
-2.0000
3.0000
0.0000
1.0000
-1.0000
Jacobi方法
（1）求解精度为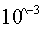时
>> A=[4 -1 0 0 0 0 0 0 0 0;-1 4 -1 0 0 0 0 0 0 0;0 -1 4 -1 0 0 0 0 0 0;0 0 -1 4 -1 0 0 0 0 0;0 0 0 -1 4 -1 0 0 0 0;0 0 0 0 -1 4 -1 0 0 0;0 0 0 0 0 -1 4 -1 0 0;0 0 0 0 0 0 -1 4 -1 0;0 0 0 0 0 0 0 -1 4 -1;0 0 0 0 0 0 0 0 -1 4];
b=[7 5 -13 2 6 -12 14 -4 5 -5]';
x0=[0 0 0 0 0 0 0 0 0 0]';
[x,k]=Jacobi(A,b,x0,1e-3)
运行结果
x =
2.0000
1.0000
-3.0001
0.0001
0.9999
-1.9999
2.9998
0.0001
0.9999
-1.0000
k =
12
（2）精度为时
>> A=[4 -1 0 0 0 0 0 0 0 0;-1 4 -1 0 0 0 0 0 0 0;0 -1 4 -1 0 0 0 0 0 0;0 0 -1 4 -1 0 0 0 0 0;0 0 0 -1 4 -1 0 0 0 0;0 0 0 0 -1 4 -1 0 0 0;0 0 0 0 0 -1 4 -1 0 0;0 0 0 0 0 0 -1 4 -1 0;0 0 0 0 0 0 0 -1 4 -1;0 0 0 0 0 0 0 0 -1 4];
b=[7 5 -13 2 6 -12 14 -4 5 -5]';
x0=[0 0 0 0 0 0 0 0 0 0]';
[x,k]=Jacobi(A,b,x0,1e-4)
实验结果
x =
2.0000
1.0000
-3.0000
-0.0000
1.0000
-2.0000
3.0000
-0.0000
1.0000
-1.0000
k =
15
（3）精度为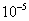时
>> A=[4 -1 0 0 0 0 0 0 0 0;-1 4 -1 0 0 0 0 0 0 0;0 -1 4 -1 0 0 0 0 0 0;0 0 -1 4 -1 0 0 0 0 0;0 0 0 -1 4 -1 0 0 0 0;0 0 0 0 -1 4 -1 0 0 0;0 0 0 0 0 -1 4 -1 0 0;0 0 0 0 0 0 -1 4 -1 0;0 0 0 0 0 0 0 -1 4 -1;0 0 0 0 0 0 0 0 -1 4];
b=[7 5 -13 2 6 -12 14 -4 5 -5]';
x0=[0 0 0 0 0 0 0 0 0 0]';
[x,k]=Jacobi(A,b,x0,1e-5)
实验结果
x =
2.0000
1.0000
-3.0000
0.0000
1.0000
-2.0000
3.0000
0.0000
1.0000
-1.0000
k =
18
结论 由实验结果可知该方程组使用Jacobi迭代法是具有很好的收敛速度。
Gauss-seidel迭代法
（1）求解精度为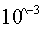时
>> A=[4 -1 0 0 0 0 0 0 0 0;-1 4 -1 0 0 0 0 0 0 0;0 -1 4 -1 0 0 0 0 0 0;0 0 -1 4 -1 0 0 0 0 0;0 0 0 -1 4 -1 0 0 0 0;0 0 0 0 -1 4 -1 0 0 0;0 0 0 0 0 -1 4 -1 0 0;0 0 0 0 0 0 -1 4 -1 0;0 0 0 0 0 0 0 -1 4 -1;0 0 0 0 0 0 0 0 -1 4];
b=[7 5 -13 2 6 -12 14 -4 5 -5]';
x=[0 0 0 0 0 0 0 0 0 0]';
[x,k]=Gaussseidel(A,b,x,1e-3,1000)
实验结果
x =
1.9999
0.9998
-3.0002
-0.0001
1.0000
-2.0000
3.0000
0.0000
1.0000
-1.0000
k =
7
（2）精度为时
>> A=[4 -1 0 0 0 0 0 0 0 0;-1 4 -1 0 0 0 0 0 0 0;0 -1 4 -1 0 0 0 0 0 0;0 0 -1 4 -1 0 0 0 0 0;0 0 0 -1 4 -1 0 0 0 0;0 0 0 0 -1 4 -1 0 0 0;0 0 0 0 0 -1 4 -1 0 0;0 0 0 0 0 0 -1 4 -1 0;0 0 0 0 0 0 0 -1 4 -1;0 0 0 0 0 0 0 0 -1 4];
b=[7 5 -13 2 6 -12 14 -4 5 -5]';
x=[0 0 0 0 0 0 0 0 0 0]';
[x,k]=Gaussseidel(A,b,x,1e-4,1000)
实验结果
x =
2.0000
1.0000
-3.0000
-0.0000
1.0000
-2.0000
3.0000
0.0000
1.0000
-1.0000
k =
9
（3）精度为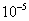时
>> A=[4 -1 0 0 0 0 0 0 0 0;-1 4 -1 0 0 0 0 0 0 0;0 -1 4 -1 0 0 0 0 0 0;0 0 -1 4 -1 0 0 0 0 0;0 0 0 -1 4 -1 0 0 0 0;0 0 0 0 -1 4 -1 0 0 0;0 0 0 0 0 -1 4 -1 0 0;0 0 0 0 0 0 -1 4 -1 0;0 0 0 0 0 0 0 -1 4 -1;0 0 0 0 0 0 0 0 -1 4];
b=[7 5 -13 2 6 -12 14 -4 5 -5]';
x=[0 0 0 0 0 0 0 0 0 0]';
[x,k]=Gaussseidel(A,b,x,1e-5,1000)
实验结果
x =
2.0000
1.0000
-3.0000
-0.0000
1.0000
-2.0000
3.0000
-0.0000
1.0000
-1.0000
k = 11
结论 由实验结果可知Gauss-seidel迭代法具有更好的收敛速度。
SOR迭代法
（1）ω=0.8时
?求解精度为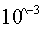时
>> A=[4 -1 0 0 0 0 0 0 0 0;-1 4 -1 0 0 0 0 0 0 0;0 -1 4 -1 0 0 0 0 0 0;0 0 -1 4 -1 0 0 0 0 0;0 0 0 -1 4 -1 0 0 0 0;0 0 0 0 -1 4 -1 0 0 0;0 0 0 0 0 -1 4 -1 0 0;0 0 0 0 0 0 -1 4 -1 0;0 0 0 0 0 0 0 -1 4 -1;0 0 0 0 0 0 0 0 -1 4];
b=[7 5 -13 2 6 -12 14 -4 5 -5]';
x0=[0 0 0 0 0 0 0 0 0 0]';
[x,k]=SOR(A,b,x0,1e-3,1000,0.8)
实验结果
x =
2.0003
1.0001
-3.0002
-0.0005
0.9994
-2.0006
2.9996
-0.0002
0.9999
-1.0000
k =
9
?精度为时
>> A=[4 -1 0 0 0 0 0 0 0 0;-1 4 -1 0 0 0 0 0 0 0;0 -1 4 -1 0 0 0 0 0 0;0 0 -1 4 -1 0 0 0 0 0;0 0 0 -1 4 -1 0 0 0 0;0 0 0 0 -1 4 -1 0 0 0;0 0 0 0 0 -1 4 -1 0 0;0 0 0 0 0 0 -1 4 -1 0;0 0 0 0 0 0 0 -1 4 -1;0 0 0 0 0 0 0 0 -1 4];
b=[7 5 -13 2 6 -12 14 -4 5 -5]';
x0=[0 0 0 0 0 0 0 0 0 0]';
[x,k]=SOR(A,b,x0,1e-4,1000,0.8)
实验结果
x =
2.0000
1.0000
-3.0000
-0.0001
0.9999
-2.0000
3.0000
-0.0000
1.0000
-1.0000
k =
12
?精度为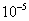时
>> A=[4 -1 0 0 0 0 0 0 0 0;-1 4 -1 0 0 0 0 0 0 0;0 -1 4 -1 0 0 0 0 0 0;0 0 -1 4 -1 0 0 0 0 0;0 0 0 -1 4 -1 0 0 0 0;0 0 0 0 -1 4 -1 0 0 0;0 0 0 0 0 -1 4 -1 0 0;0 0 0 0 0 0 -1 4 -1 0;0 0 0 0 0 0 0 -1 4 -1;0 0 0 0 0 0 0 0 -1 4];
b=[7 5 -13 2 6 -12 14 -4 5 -5]';
x0=[0 0 0 0 0 0 0 0 0 0]';
[x,k]=SOR(A,b,x0,1e-5,1000,0.8)
实验结果
x =
2.0000
1.0000
-3.0000
-0.0000
1.0000
-2.0000
3.0000
-0.0000
1.0000
-1.0000
k =
15
（2）ω=0.9时
?求解精度为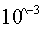时
>> A=[4 -1 0 0 0 0 0 0 0 0;-1 4 -1 0 0 0 0 0 0 0;0 -1 4 -1 0 0 0 0 0 0;0 0 -1 4 -1 0 0 0 0 0;0 0 0 -1 4 -1 0 0 0 0;0 0 0 0 -1 4 -1 0 0 0;0 0 0 0 0 -1 4 -1 0 0;0 0 0 0 0 0 -1 4 -1 0;0 0 0 0 0 0 0 -1 4 -1;0 0 0 0 0 0 0 0 -1 4];
b=[7 5 -13 2 6 -12 14 -4 5 -5]';
x0=[0 0 0 0 0 0 0 0 0 0]';
[x,k]=SOR(A,b,x0,1e-3,1000,0.9)
实验结果
x =
2.0000
0.9999
-3.0003
-0.0003
0.9997
-2.0002
2.9999
-0.0000
1.0000
-1.0000
k =
8
?精度为时
>> A=[4 -1 0 0 0 0 0 0 0 0;-1 4 -1 0 0 0 0 0 0 0;0 -1 4 -1 0 0 0 0 0 0;0 0 -1 4 -1 0 0 0 0 0;0 0 0 -1 4 -1 0 0 0 0;0 0 0 0 -1 4 -1 0 0 0;0 0 0 0 0 -1 4 -1 0 0;0 0 0 0 0 0 -1 4 -1 0;0 0 0 0 0 0 0 -1 4 -1;0 0 0 0 0 0 0 0 -1 4];
b=[7 5 -13 2 6 -12 14 -4 5 -5]';
x0=[0 0 0 0 0 0 0 0 0 0]';
[x,k]=SOR(A,b,x0,1e-4,1000,0.9)
实验结果
x =
2.0000
1.0000
-3.0000
-0.0000
1.0000
-2.0000
3.0000
-0.0000
1.0000
-1.0000
k =
10
?精度为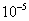时
>> A=[4 -1 0 0 0 0 0 0 0 0;-1 4 -1 0 0 0 0 0 0 0;0 -1 4 -1 0 0 0 0 0 0;0 0 -1 4 -1 0 0 0 0 0;0 0 0 -1 4 -1 0 0 0 0;0 0 0 0 -1 4 -1 0 0 0;0 0 0 0 0 -1 4 -1 0 0;0 0 0 0 0 0 -1 4 -1 0;0 0 0 0 0 0 0 -1 4 -1;0 0 0 0 0 0 0 0 -1 4];
b=[7 5 -13 2 6 -12 14 -4 5 -5]';
x0=[0 0 0 0 0 0 0 0 0 0]';
[x,k]=SOR(A,b,x0,1e-5,1000,0.9)
实验结果
x =
2.0000
1.0000
-3.0000
-0.0000
1.0000
-2.0000
3.0000
-0.0000
1.0000
-1.0000
k =
13
（3）ω=1.0时
?求解精度为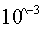时
>> A=[4 -1 0 0 0 0 0 0 0 0;-1 4 -1 0 0 0 0 0 0 0;0 -1 4 -1 0 0 0 0 0 0;0 0 -1 4 -1 0 0 0 0 0;0 0 0 -1 4 -1 0 0 0 0;0 0 0 0 -1 4 -1 0 0 0;0 0 0 0 0 -1 4 -1 0 0;0 0 0 0 0 0 -1 4 -1 0;0 0 0 0 0 0 0 -1 4 -1;0 0 0 0 0 0 0 0 -1 4];
b=[7 5 -13 2 6 -12 14 -4 5 -5]';
x0=[0 0 0 0 0 0 0 0 0 0]';
[x,k]=SOR(A,b,x0,1e-3,1000,1.0)
实验结果
x =
1.9999
0.9998
-3.0002
-0.0001
1.0000
-2.0000
3.0000
0.0000
1.0000
-1.0000
k =
7
?精度为时
>> A=[4 -1 0 0 0 0 0 0 0 0;-1 4 -1 0 0 0 0 0 0 0;0 -1 4 -1 0 0 0 0 0 0;0 0 -1 4 -1 0 0 0 0 0;0 0 0 -1 4 -1 0 0 0 0;0 0 0 0 -1 4 -1 0 0 0;0 0 0 0 0 -1 4 -1 0 0;0 0 0 0 0 0 -1 4 -1 0;0 0 0 0 0 0 0 -1 4 -1;0 0 0 0 0 0 0 0 -1 4];
b=[7 5 -13 2 6 -12 14 -4 5 -5]';
x0=[0 0 0 0 0 0 0 0 0 0]';
[x,k]=SOR(A,b,x0,1e-4,1000,1.0)
实验结果
x =
2.0000
1.0000
-3.0000
-0.0000
1.0000
-2.0000
3.0000
0.0000
1.0000
-1.0000
k =
9
?精度为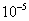时
>> A=[4 -1 0 0 0 0 0 0 0 0;-1 4 -1 0 0 0 0 0 0 0;0 -1 4 -1 0 0 0 0 0 0;0 0 -1 4 -1 0 0 0 0 0;0 0 0 -1 4 -1 0 0 0 0;0 0 0 0 -1 4 -1 0 0 0;0 0 0 0 0 -1 4 -1 0 0;0 0 0 0 0 0 -1 4 -1 0;0 0 0 0 0 0 0 -1 4 -1;0 0 0 0 0 0 0 0 -1 4];
b=[7 5 -13 2 6 -12 14 -4 5 -5]';
x0=[0 0 0 0 0 0 0 0 0 0]';
[x,k]=SOR(A,b,x0,1e-5,1000,1.0)
实验结果
x =
2.0000
1.0000
-3.0000
-0.0000
1.0000
-2.0000
3.0000
-0.0000
1.0000
-1.0000
k =
11
（4）ω=1.1时
?求解精度为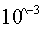时
>> A=[4 -1 0 0 0 0 0 0 0 0;-1 4 -1 0 0 0 0 0 0 0;0 -1 4 -1 0 0 0 0 0 0;0 0 -1 4 -1 0 0 0 0 0;0 0 0 -1 4 -1 0 0 0 0;0 0 0 0 -1 4 -1 0 0 0;0 0 0 0 0 -1 4 -1 0 0;0 0 0 0 0 0 -1 4 -1 0;0 0 0 0 0 0 0 -1 4 -1;0 0 0 0 0 0 0 0 -1 4];
b=[7 5 -13 2 6 -12 14 -4 5 -5]';
x0=[0 0 0 0 0 0 0 0 0 0]';
[x,k]=SOR(A,b,x0,1e-3,1000,1.1)
实验结果
x =
1.9999
1.0000
-3.0000
-0.0000
1.0000
-2.0000
3.0000
-0.0000
1.0000
-1.0000
k =
8
?精度为时
>> A=[4 -1 0 0 0 0 0 0 0 0;-1 4 -1 0 0 0 0 0 0 0;0 -1 4 -1 0 0 0 0 0 0;0 0 -1 4 -1 0 0 0 0 0;0 0 0 -1 4 -1 0 0 0 0;0 0 0 0 -1 4 -1 0 0 0;0 0 0 0 0 -1 4 -1 0 0;0 0 0 0 0 0 -1 4 -1 0;0 0 0 0 0 0 0 -1 4 -1;0 0 0 0 0 0 0 0 -1 4];
b=[7 5 -13 2 6 -12 14 -4 5 -5]';
x0=[0 0 0 0 0 0 0 0 0 0]';
[x,k]=SOR(A,b,x0,1e-4,1000,1.1)
实验结果
x =
2.0000
1.0000
-3.0000
0.0000
1.0000
-2.0000
3.0000
0.0000
1.0000
-1.0000
k =
9
?精度为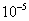时
>> A=[4 -1 0 0 0 0 0 0 0 0;-1 4 -1 0 0 0 0 0 0 0;0 -1 4 -1 0 0 0 0 0 0;0 0 -1 4 -1 0 0 0 0 0;0 0 0 -1 4 -1 0 0 0 0;0 0 0 0 -1 4 -1 0 0 0;0 0 0 0 0 -1 4 -1 0 0;0 0 0 0 0 0 -1 4 -1 0;0 0 0 0 0 0 0 -1 4 -1;0 0 0 0 0 0 0 0 -1 4];
b=[7 5 -13 2 6 -12 14 -4 5 -5]';
x0=[0 0 0 0 0 0 0 0 0 0]';
[x,k]=SOR(A,b,x0,1e-5,1000,1.1)
实验结果
x =
2.0000
1.0000
-3.0000
0.0000
1.0000
-2.0000
3.0000
0.0000
1.0000
-1.0000
k =
11
（5）ω=1.2时
?求解精度为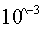时
>> A=[4 -1 0 0 0 0 0 0 0 0;-1 4 -1 0 0 0 0 0 0 0;0 -1 4 -1 0 0 0 0 0 0;0 0 -1 4 -1 0 0 0 0 0;0 0 0 -1 4 -1 0 0 0 0;0 0 0 0 -1 4 -1 0 0 0;0 0 0 0 0 -1 4 -1 0 0;0 0 0 0 0 0 -1 4 -1 0;0 0 0 0 0 0 0 -1 4 -1;0 0 0 0 0 0 0 0 -1 4];
b=[7 5 -13 2 6 -12 14 -4 5 -5]';
x0=[0 0 0 0 0 0 0 0 0 0]';
[x,k]=SOR(A,b,x0,1e-3,1000,1.2)
实验结果
x =
1.9999
1.0000
-3.0000
-0.0000
1.0000
-2.0000
3.0000
-0.0000
1.0000
-1.0000
k =
10
?精度为时
>> A=[4 -1 0 0 0 0 0 0 0 0;-1 4 -1 0 0 0 0 0 0 0;0 -1 4 -1 0 0 0 0 0 0;0 0 -1 4 -1 0 0 0 0 0;0 0 0 -1 4 -1 0 0 0 0;0 0 0 0 -1 4 -1 0 0 0;0 0 0 0 0 -1 4 -1 0 0;0 0 0 0 0 0 -1 4 -1 0;0 0 0 0 0 0 0 -1 4 -1;0 0 0 0 0 0 0 0 -1 4];
b=[7 5 -13 2 6 -12 14 -4 5 -5]';
x0=[0 0 0 0 0 0 0 0 0 0]';
[x,k]=SOR(A,b,x0,1e-4,1000,1.2)
实验结果
x =
2.0000
1.0000
-3.0000
-0.0000
1.0000
-2.0000
3.0000
-0.0000
1.0000
-1.0000
k =
12
?精度为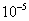时
>> A=[4 -1 0 0 0 0 0 0 0 0;-1 4 -1 0 0 0 0 0 0 0;0 -1 4 -1 0 0 0 0 0 0;0 0 -1 4 -1 0 0 0 0 0;0 0 0 -1 4 -1 0 0 0 0;0 0 0 0 -1 4 -1 0 0 0;0 0 0 0 0 -1 4 -1 0 0;0 0 0 0 0 0 -1 4 -1 0;0 0 0 0 0 0 0 -1 4 -1;0 0 0 0 0 0 0 0 -1 4];
b=[7 5 -13 2 6 -12 14 -4 5 -5]';
x0=[0 0 0 0 0 0 0 0 0 0]';
[x,k]=SOR(A,b,x0,1e-5,1000,1.2)
实验结果
x =
2.0000
1.0000
-3.0000
0.0000
1.0000
-2.0000
3.0000
0.0000
1.0000
-1.0000
k =13
结论 由此实验数据可知松弛因子的最佳值是1 。
实验二 函数差值方法
一、实验题目 给定函数
的n+1个节点值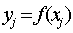
，j=0.1，... ，n 试用Lagrange方法求其n次插值多项式或分段插值多形式。
（1）给定数据如下
构造5次Lagrange插值多项式和分段2次插值多项式，并计算飞f（0.596），f（0.99）的值
（2）给定数据如下
构造6次Lagrange插值多项式，并计算f（1.8）的值
二、实验要求
（1）利用Lagrange插值公式，编制出构造差值多项式的程序
（2）根据节点的选取原则，对问题（2）用三点插值或二点插值，其计算结果如何
（3）绘出插值多项式的函数曲线，观察其光滑性
三、源程序及实验结果
Lagrange插值的程序
function y=lagrange(xi,yi,x)
m=length(xi);n=length(yi);p=length(x);
if m~=n error('数据输入有误，请重新输入');end
s=0;
for k=1:n
t=ones(1,p);
for j=1:n
if j~=k
t=t.*(x-xi(j))/(xi(k)-xi(j));
end
end
s=s+t*yi(k);
end
y=s;
第一组数据
（1）5次Lagrange插值多项式
插值多项式为
>> syms x;
>> xi=[0.4,0.55,0.65,0.80,0.95,1.05];
yi=[0.41075,0.57815,0.69675,0.90,1.00,1.25382];
y=lagrange(xi,yi,x)
y =
640*((5*x)/2 - 1)*(x - 11/20)*(x - 13/20)*(x - 19/20)*(x - 21/20) - (4645*(4*x - 8/5)*(x - 4/5)*(x - 11/20)*(x - 19/20)*(x - 21/20))/12 + (11563*((20*x)/3 - 8/3)*(x - 4/5)*(x - 13/20)*(x - 19/20)*(x - 21/20))/100 - (1643*((20*x)/3 - 11/3)*(x - 4/5)*(x - 13/20)*(x - 19/20)*(x - 21/20))/143 - (5000*((20*x)/11 - 8/11)*(x - 4/5)*(x - 11/20)*(x - 13/20)*(x - 21/20))/9 + (62691*((20*x)/13 - 8/13)*(x - 4/5)*(x - 11/20)*(x - 13/20)*(x - 19/20))/250
>> y=simple(y)
y =
(3913328*x^5)/32175 - (45339971*x^4)/107250 + (1842233513*x^3)/3217500 - (5394744687*x^2)/14300000 + (31395551227*x)/257400000 - 56566963/3750000
该函数的图像为
x=[0.4:0.005:1.2];
>> y=(3913328.*x.^5)/32175 - (45339971.*x.^4)/107250 + (1842233513.*x.^3)/3217500 - (5394744687.*x.^2)/14300000 + (31395551227.*x)/257400000 - 56566963/3750000;plot(x,y)
x=0.596时的值
>> xi=[0.4,0.55,0.65,0.80,0.95,1.05];
yi=[0.41075,0.57815,0.69675,0.90,1.00,1.25382];
y=lagrange(xi,yi,0.596)
y =
0.6257
x=0.99时的值
>> xi=[0.4,0.55,0.65,0.80,0.95,1.05];
yi=[0.41075,0.57815,0.69675,0.90,1.00,1.25382];
y=lagrange(xi,yi,0.99)
y =
1.0542
（2）分段2次插值多项式
? 选取xj=0.55，0.80,1.05进行2次插值时
插值多项式为
>> syms x;
>> xi=[0.55,0.80,1.05];
yi=[0.57815,0.90,1.25382];
y=lagrange(xi,yi,x)
y =
(62691*(2*x - 11/10)*(x - 4/5))/12500 - (18*(4*x - 11/5)*(x - 21/20))/5 + (11563*(4*x - 16/5)*(x - 21/20))/10000
>> y=simple(y)
y =
(3197*x^2)/12500 + (235531*x)/250000 - 5433/312500
多项式函数的图像
>> x=[0.5:0.001:1.2];
>> y=(3197.*x.^2)/12500 + (235531.*x)/250000 - 5433/312500;plot(x,y)
计算x=0.596时的值，求得函数值为
>> xi=[0.55,0.80,1.05];
yi=[0.57815,0.90,1.25382];
y=lagrange(xi,yi,0.596)
y =
0.6350
计算x=0.99时的值，求得函数值为
>> xi=[0.55,0.80,1.05];
yi=[0.57815,0.90,1.25382];
y=lagrange(xi,yi,0.99)
y =
1.1660
?选取xj=0.65,0.80,0.95进行2次插值
插值多项式为
>> syms x;
xi=[0.65,0.80,0.95];
yi=[0.69675,0.90,1.00];
y=lagrange(xi,yi,x)
y =
(20*((10*x)/3 - 13/6)*(x - 4/5))/3 - 6*((20*x)/3 - 13/3)*(x - 19/20) + (929*((20*x)/3 - 16/3)*(x - 19/20))/400
>> y=simple(y)
y =
(3371*x)/720 - (413*x^2)/180 - 6197/4500
该函数图像为
>> x=[0.5:0.001:1.00];
>> y=(3371.*x)/720 - (413.*x.^2)/180 - 6197/4500;plot(x,y)
计算x=0.596时的值，求得函数值为
>> xi=[0.65,0.80,0.95];
yi=[0.69675,0.90,1.00];
y=lagrange(xi,yi,0.596)
y =
0.5983
计算x=0.99时的值，求得函数值为
>> xi=[0.65,0.80,0.95];
yi=[0.69675,0.90,1.00];
y=lagrange(xi,yi,0.99)
y =
1.0092
第二组数据
（1）6次Lagrange插值多项式
插值多项式为
>> syms x;
>> xi=[1,2,3,4,5,6,7];
yi=[0.368,0.135,0.050,0.018,0.007,0.002,0.001];
y=lagrange(xi,yi,x)
y =
(23*(x - 2)*(x - 3)*(x - 4)*(x - 5)*(x - 6)*(x - 7))/45000 - (9*(x - 1)*(x - 3)*(x - 4)*(x - 5)*(x - 6)*(x - 7))/8000 + ((x/2 - 1/2)*(x - 2)*(x - 4)*(x - 5)*(x - 6)*(x - 7))/480 - (3*(x/3 - 1/3)*(x - 2)*(x - 3)*(x - 5)*(x - 6)*(x - 7))/2000 + (7*(x/4 - 1/4)*(x - 2)*(x - 3)*(x - 4)*(x - 6)*(x - 7))/12000 - ((x/5 - 1/5)*(x - 2)*(x - 3)*(x - 4)*(x - 5)*(x - 7))/12000 + ((x/6 - 1/6)*(x - 2)*(x - 3)*(x - 4)*(x - 5)*(x - 6))/120000
>> y=simple(y)
y =
(7*x^6)/120000 - (193*x^5)/120000 + (223*x^4)/12000 - (2821*x^3)/24000 + (53023*x^2)/120000 - (19367*x)/20000 + 199/200
多项式图像为
>> x=[0:0.05:8];
>> y=(7.*x.^6)/120000 - (193.*x.^5)/120000 + (223.*x.^4)/12000 - (2821.*x.^3)/24000 + (53023.*x.^2)/120000 - (19367.*x)/20000 + 199/200;plot(x,y)
计算求得先x=1.8时的值
>> xi=[1,2,3,4,5,6,7];
yi=[0.368,0.135,0.050,0.018,0.007,0.002,0.001];
y=lagrange(xi,yi,1.8)
y =
0.1648
（2）二点插值
插值多项式为
>> syms x;
>> xi=[1,2];
yi=[0.368,0.135];
y=lagrange(xi,yi,x)
y =
601/1000 - (233*x)/1000
图像为
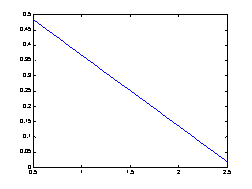
X=1.8时函数值为
>> xi=[1,2];
yi=[0.368,0.135];
y=lagrange(xi,yi,1.8)
y =
0.1816
（3）三点插值
插值多项式为
>> syms x;
>> xi=[1,2,3];
yi=[0.368,0.135,0.050];
y=lagrange(xi,yi,x)
y =
(23*(x - 2)*(x - 3))/125 - (27*(x - 1)*(x - 3))/200 + ((x/2 - 1/2)*(x - 2))/20
>> y=simple(y)
y =
(37*x^2)/500 - (91*x)/200 + 749/1000
图像为
>> x=[0.5:0.05:3.5];
y=(37.*x.^2)/500 - (91.*x)/200 + 749/1000;plot(x,y)
X=1.8时函数值为
>> xi=[1,2,3];
yi=[0.368,0.135,0.050];
y=lagrange(xi,yi,1.8)
y =
0.1698
-
东北大学物理实验报告
实验一霍尔效应及其应用预习思考题1列出计算霍尔系数载流子浓度n电导率及迁移率的计算公式并注明单位霍尔系数载流子浓度电导率迁移率2如…
- 东北大学大物实验报告(含灵敏电流计)
-
东北大学物理实验电桥的使用 实际体会详细过程
1实验前进教室以后把书包什么的放到一个角落里不能放实验台上占地方把实验报告和书拿出来最好再拿个本好随时记老师说的注意事项教室的黑板…
-
东北大学15秋学期《大学物理Ⅰ》在线作业3答案
谋学网15秋学期大学物理在线作业3单选题一单选题共20道试题共100分1选择22R24R2R2R2选择3题面为图片选择4题面为图片…
- 东北大学大物实验灵敏电流计
-
东北大学物理实验报告
实验一霍尔效应及其应用预习思考题1列出计算霍尔系数载流子浓度n电导率及迁移率的计算公式并注明单位霍尔系数载流子浓度电导率迁移率2如…
-
东大中学九年级物理实验计划
东大中学九年级物理实验计划一指导思想物理实验是学生进行科学探究的重要方式实验室则是学生学习和进行实验的主要场所是物理探究学习的主要…
- 东北大学大物实验报告(含灵敏电流计)
-
东北大学计算机硬件基础实验报告
东北大学计算机硬件技术基础实验报告专业班级姓名学号实验题目循环程序设计日期实验目的1加深对循环设计的理解2掌握循环程序的设计方法3…
-
东北大学 物理实验 拉伸法杨氏模量的测量 实际体会详细过程
实验报告没什么可说的该实验的原理和步骤都不多地方足够都写上了表格要画好另外去实验室的时候带把尺子吧实验的时候会用上再带12张纸同样…
-
20xx中国私人财富报告
20xx中国私人财富报告贝恩公司与中国招商银行联合发布20xx年4月20日在个人高端客户金融服务领域享有盛誉的招商银行和全球知名咨…