数值分析课程设计报告

《数值分析 Numerical Analysis》

课程设计

系专：

班级：

姓名：

学号：

指导老师：

实验一

1．1 水手、猴子和椰子问题：五个水手带了一只猴子来到南太平洋的一个荒岛上，发现那里有一大堆椰子。由于旅途的颠簸，大家都很疲惫，很快就入睡了。第一个水手醒来后，把椰子平分成五堆，将多余的一只给了猴子，他私藏了一堆后便又去睡了。第二、第三、第四、第五个水手也陆续起来，和第一个水手一样，把椰子分成五堆，恰多一只猴子，私藏一堆，再去入睡，天亮以后，大家把余下的椰子重新等分成五堆，每人分一堆，正好余一只再给猴子，试问原先共有几只椰子？试分析椰子数目的变化规律，利用逆向递推的方法求解这一问题（15621）。

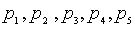问题分析：设最初的椰子数为，即第一个水手所处理之前的椰子数，用分别表示五个水手对椰子动了手脚以后剩余的椰子数目，则根据问题有。再用x表示最后每个水手平分得到的椰子数，于是有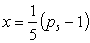。所以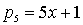，利用逆向递推的方法，有。由于椰子数为一正整数，用任意的x作为初值递推出的数据不一定是合适的。这里用 for 循环语句结合 break语句来寻找合适的 x 和，对任意的 x 递推计算出，当计算结果为正整数时，结果正确，否则选取另外的 x 再次重新递推计算，直到计算出的结果 p0为正整数为止。

程序设计：

n=input('input n：');

for x=1:n

p=5*x+1;

for k=1:5

p=5*p/4+1;

end

if p==fix(p),break,end

end

disp([x,p])

运行结果：input n：122

1.0e+003 *

0.1220 1.8728

input n：1200

1023 15621

input n：4567890

1023 15621

1．2 设，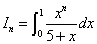

① 从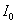尽可能精确的近似值出发，利用递推公式：

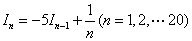
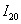计算机从到的近似值；

解：先求出I₀的精确值，再用递推公式

syms x;

I₀=int(1/(5+x),x,0,1);

I₀=vpa(I₀);

for i=1:20

I₀=-5*I₀+1/i

End

经过20次迭代，最终结果为I0 =0.007997523028232163831452112940177

② 从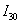较粗糙的估计值出发，用递推公式：

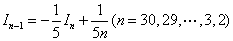
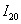计算从到的近似值；

解：先求出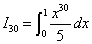的值近似精确值，再用递推公式

syms x;

I₀=int(0.2*x^30,x,0,1);

I₀=vpa(I₀);

for i=30:-1:2

I₀=-0.2*I₀+0.2/i

End

经过30次迭代，最终结果为I₀ = 0.088392216030226868941404253296685

③ 分析所得结果的可靠性以及出现这种现象的原因。

解：方法2比较可靠，因为方法1每次都将误差放大5倍，而方法2则将误差缩小到原来的0.2倍。

实验二

2．1 用高斯消元法的消元过程作矩阵分解。设

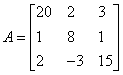
消元过程可将矩阵A化为上三角矩阵U，试求出消元过程所用的乘数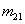、、并以如下格式构造下三角矩阵L和上三角矩阵U

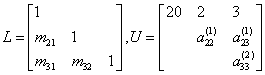
验证：矩阵A可以分解为L和U的乘积，即A=LU。

解：

算法分析：由于matlab中含有将A分解成一个下三角矩阵和一个上三角矩阵，所以直接调用。

程序及其运行结果： A=[20 2 3;1 8 1;2 -3 15]

[L,U]=lu(A)

A =

20 2 3

1 8 1

2 -3 15

L =

1.0000 0 0

0.0500 1.0000 0

0.1000 -0.4051 1.0000

U =

20.0000 2.0000 3.0000

0 7.9000 0.8500

0 0 15.0443

矩阵A可以分解为L和U的乘积

2.3 验证希尔伯特矩阵的病态性：对于三阶矩阵

取右端向量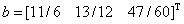，验证：

（1）向量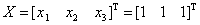是方程组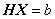的准确解；

（2）取右端向量b的三位有效数字得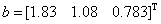，求方程组的准确解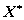，并与X的数据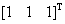作比较。说明矩阵的病态性。

解：(1) 直接验证即可

A=[1 1/2 1/3;1/2 1/3 1/4;1/3 1/4 1/5];

B=[1;1;1];

b=sym(A*B)

结果与上述结果相同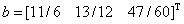

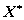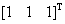(2) 先求出解，与数据作比较。

A=[1 1/2 1/3;1/2 1/3 1/4;1/3 1/4 1/5];

b=[1.83;1.08;0.783];

B=A\b

结果为

B =

1.079999999999999

0.540000000000004

1.439999999999997

结果误差变化较大，说明数值的微小变化导致结果的巨大误差，矩阵A为病态的

实验三

3．1 用泰勒级数的有限项逼近正弦函数

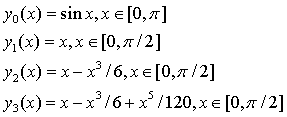
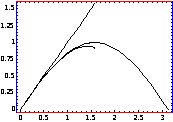
用计算机绘出上面四个函数的图形。

解：程序：

x=0:pi/100:pi;

m=0:pi/100:pi/2;

y0=sin(x);

y1=m;

y2=m-m.^3/6;

y3=m-m.^3/6+t.^5/120;

plot(x,y0,m,y1,m,y2,m,y3)

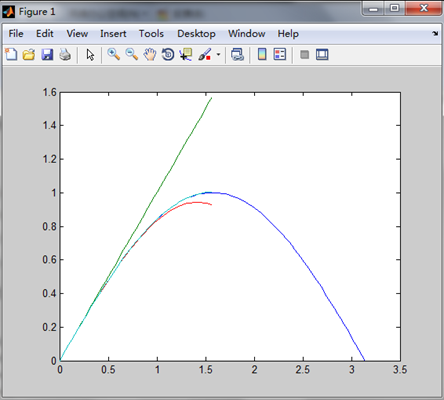运行结果：

3．2 绘制飞机的降落曲线

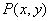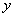一架飞机飞临北京国际机场上空时，其水平速度为540km/h，飞行高度为1 000m。飞机从距机场指挥塔的横向距离12 000m处开始降落。根据经验，一架水平飞行的飞机其降落曲线是一条三次曲线。建立直角坐标系，设飞机着陆点为原点O，降落的飞机为动点，则表示飞机距指挥塔的距离，表示飞机的飞行高度，降落曲线为

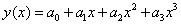
该函数满足条件：

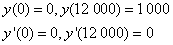
（1）试利用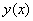满足的条件确定三次多项式中的四个系数；

（2）用所求出的三次多项式函数绘制出飞机降落曲线。

解：

（1）程序：

A=[1 0 0 0;1 12000 12000^2 12000^3;0 1 0 0;0 1 24000 3*(12000^2)];

b=[0,1000,0,0]';

inv(A)*b

运行结果：ans =

1.0e-004 *

0.2083

-0.0000

（2）程序：x=0:50:12000;

y=0.207e-004*(x.^2)+-0.00001158e-004*(x.^3);

plot(x,y)

运行结果：

实验四

4．1 曾任英特尔公司董事长的摩尔先生早在1965年时，就观察到一件很有趣的现象：集成电路上可容纳的零件数量，每隔一年半左右就会增长一倍，性能也提升一倍。因而发表论文，提出了大大有名的摩尔定律（Moore’s Law），并预测未来这种增长仍会延续下去。下面数据中，第二行数据为晶片上晶体数目在不同年代与1959年时数目比较的倍数。这些数据是推出摩尔定律的依据：

试从表中数据出发，推导线性拟合的函数表达式。

程序设计：

y=[1 3 4 5 6];

x2=[1959 1962 1963 1964 1965];

P=polyfit(x2,y,1);

disp(P);

运行结果为： 1.0e+003 *

0.0008 -1.6255

结果分析：由运行结果可知线性拟合的函数表达式为y= 0.0008x -1.6255，由于是近似值，所以不免有误差。

实验五

5．1 用几种不同的方法求积分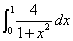的值。

（1）牛顿-莱布尼茨公式；（2）梯形公式；（3）辛卜生公式；（4）复合梯形公式。

解：（1）牛顿-莱布尼茨公式

输入：

syms x;

y=4/(1+x^2);

int_y=int(y,x,0,1)

输出：

int_y =

（2）梯形公式

function y=dada(x)

y=4./(1+x.^2);

以'dada.m'保存

输入：

T=(1-0)/2*(dada(1)+dada(0))

结果：

T =3

（3）辛卜生公式

输入：

S=quad('dada',0,1)

结果：

S =

3.141592682924567

（4）复合梯形公式

输入d=1/100;

x=0:d:1;

f=dada(x);

FT=trapz(f)*d

结果：

FT =

3.141575986923129

5．2 设X为标准正态随机变量，即X~N（0，1）。现分别取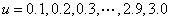，试设计算法计算30个不同的概率值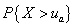；，并将计算结果与概率论教科书中的标准正态分布函数表作比较。

（提示：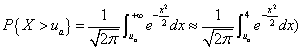

解：

m=0.1:0.1:3;

P=zeros(30,1);

for i=1:30

P(i)=1/sqrt(2*pi)*int(sym('exp(-x^2/2)'),m(i),4);

end

m=0.1:0.1:3;

P=zeros(30,1);

for i=1:30

P(i)=1/sqrt(2*pi)*int(sym('exp(-x^2/2)'),-4,m(i));

end

P =

0.4601

0.4207

0.3821

0.3445

0.3085

0.2742

0.2419

0.2118

0.1840

0.1586

0.1356

0.1150

0.0968

0.0807

0.0668

0.0548

0.0445

0.0359

0.0287

0.0227

0.0178

0.0139

0.0107

0.0082

0.0062

0.0046

0.0034

0.0025

0.0018

0.0013

P =

0.5398

0.5792

0.6179

0.6554

0.6914

0.7257

0.7580

0.7881

0.8159

0.8413

0.8643

0.8849

0.9032

0.9192

0.9332

0.9452

0.9554

0.9640

0.9713

0.9772

0.9821

0.9861

0.9892

0.9918

0.9938

0.9953

0.9965

0.9974

0.9981

0.9986

5．5 求空间曲线L：

弧长公式为

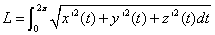
解：运行程序为：syms t;

a=diff(cos(t));

b=diff(sin(t));

c=diff(2-cos(t)-sin(t));

y=int((a^2+b^2+c^2)^0.5,t,0,2*pi);

vpa(y)

运行结果：ans =8.737752570984804741619351957708

实验六

6．1 用欧拉公式和四阶龙格-库塔法分别求解下列初值问题；

解：（1）程序：

欧拉公式：

function [t,x]=Euler(fun,t0,tt,x0,N)

h=(tt-t0)/N;

t=t0+[0:N]'*h;

x(1,:)=x0';

for k=1:N

f=feval(fun,t(k),x(k,:));

f=f';

x(k+1,:)=x(k,:)+h*f;

end

以'Euler.m'保存

function f=Euler_fun(t,x)

f=0.9*x./(1+2*t);

以'Euler_fun.m'保存

function main_Euler

[t,x]=Euler('Euler_fun',0,1,1,20);

fh=dsolve('Dx=0.9*x/(1+2*t)','x(0)=1');

for k=1:21

ft(k)=t(k);

fx(k)=subs(fh,ft(k));

end

[t,x]

以'main_Euler.m'保存

输入：main_Euler

ans =

0 1.0000

0.0500 1.0450

0.1000 1.0878

0.1500 1.1285

0.2000 1.1676

0.2500 1.2051

0.3000 1.2413

0.3500 1.2762

0.4000 1.3100

0.4500 1.3427

0.5000 1.3745

0.5500 1.4055

0.6000 1.4356

0.6500 1.4649

0.7000 1.4936

0.7500 1.5216

0.8000 1.5490

0.8500 1.5758

0.9000 1.6021

0.9500 1.6278

1.0000 1.6531

四阶龙格-库塔法

function R=rk4(f,a,b,ya,N)

h=(b-a)/N;

T=zeros(1,N+1);

Y=zeros(1,N+1);

T=a:h:b;

Y(1)=ya;

for j=1:N

k1=h*feval(f,T(j),Y(j));

k2=h*feval(f,T(j)+h/2,Y(j)+k1/2);

k3=h*feval(f,T(j)+h/2,Y(j)+k2/2);

k4=h*feval(f,Y(j)+h,Y(j)+k3);

Y(j+1)=Y(j)+(k1+2*k2+2*k3+k4)/6;

end

ans=[T' Y']

以'rk4.m'保存

function z=f(x,y)

z=0.9*y./(1+2*x);

以'f.m'保存

输入：rk4('f',0,1,1,20)

结果：

ans =

0 1.0000

0.0500 1.0392

0.1000 1.0765

0.1500 1.1121

0.2000 1.1463

0.2500 1.1791

0.3000 1.2108

0.3500 1.2415

0.4000 1.2712

0.4500 1.3000

0.5000 1.3281

0.5500 1.3554

0.6000 1.3821

0.6500 1.4082

0.7000 1.4337

0.7500 1.4586

0.8000 1.4831

0.8500 1.5071

0.9000 1.5306

0.9500 1.5538

1.0000 1.5765

（2）程序：欧拉公式

function [t,x]=Eulers(fun,t0,tt,x0,N)

h=(tt-t0)/N;

t=t0+[0:N]'*h;

x(1,:)=x0';

for k=1:N

f=feval(fun,t(k),x(k,:));

f=f';

x(k+1,:)=x(k,:)+h*f;

end

以'Eulers.m'保存

function f=Euler_funs(t,x)

f=-t*x/(1+t^2);

以'Euler_funs.m'保存

function mains_Euler

[t,x]=Euler('Euler_funs',0,1,2,20);

fh=dsolve('Dx=0.9*x/(1+2*t)','x(0)=1');

for k=1:21

ft(k)=t(k);

fx(k)=subs(fh,ft(k));

end

[t,x]

以'mains_Euler.m'保存

输入：mains_Euler

结果：

ans =

0 2.0000

0.0500 2.0000

0.1000 1.9950

0.1500 1.9851

0.2000 1.9706

0.2500 1.9516

0.3000 1.9287

0.3500 1.9021

0.4000 1.8725

0.4500 1.8402

0.5000 1.8058

0.5500 1.7696

0.6000 1.7323

0.6500 1.6941

0.7000 1.6554

0.7500 1.6165

0.8000 1.5777

0.8500 1.5392

0.9000 1.5012

0.9500 1.4639

1.0000 1.4274

四阶龙格-库塔法

function R=rk4s(f,a,b,ya,N)

h=(b-a)/N;

T=zeros(1,N+1);

Y=zeros(1,N+1);

T=a:h:b;

Y(1)=ya;

for j=1:N

k1=h*feval(f,T(j),Y(j));

k2=h*feval(f,T(j)+h/2,Y(j)+k1/2);

k3=h*feval(f,T(j)+h/2,Y(j)+k2/2);

k4=h*feval(f,Y(j)+h,Y(j)+k3);

Y(j+1)=Y(j)+(k1+2*k2+2*k3+k4)/6;

end

ans=[T' Y']

以'rk4s.m'保存

function z=fs(x,y)

z=-x*y/(1+x^2);

以'fs.m'保存

输入：rk4s('fs',0,1,2,20)

结果：

ans =

0 2.0000

0.0500 1.9918

0.1000 1.9795

0.1500 1.9632

0.2000 1.9433

0.2500 1.9200

0.3000 1.8936

0.3500 1.8645

0.4000 1.8331

0.4500 1.7998

0.5000 1.7650

0.5500 1.7291

0.6000 1.6923

0.6500 1.6551

0.7000 1.6176

0.7500 1.5801

0.8000 1.5429

0.8500 1.5060

0.9000 1.4697

0.9500 1.4340

1.0000 1.3990

6.2用求解常微分方程初值问题的方法计算积分上限函数

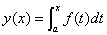
的值，实际上是将上面表达式两端求导化为常微分方程形式，并用初值条件。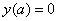

试用MATLAB中的指令ode23解决定积分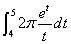的计算问题。

解：odefun=@(x,y) 2*pi*exp(x)/x; %定义函数

tspan=[4 5]; %求解区间

y0=0; %初值

[x,y]=ode23(odefun,tspan,y0)

x =

4.0000

4.0001

4.0007

4.0036

4.0182

4.0911

4.1911

4.2911

4.3911

4.4911

4.5911

4.6911

4.7911

4.8911

5.0000

y =

0.0001

0.0005

0.0025

0.0125

0.0625

0.3129

1.5732

8.0862

17.6281

27.9249

39.0424

51.0526

64.0337

78.0708

93.2571

109.6940

129.1469

当x=5时，y=129.1469

实验七

7.1用二分法求下列方程在指定区间[a，b]上的实根近似值：（要求误差不超过0.01）

(1)x-sinx-1=0，[a,b]=[1,3]；

(2)xsin x=1，[a,b]=[0,1.5].

解；（1）运行程序：

a=1;b=3;k=0;

y1=a-sin(a)-1;

while(b-a)>0.01

k=k+1;

x0=(a+b)/2;x(k)=x0;

y0=x0-sin(x0)-1;y(k)=y0;

if y0*y1<0

b=x0;

else

a=x0;

y1=y0;

end

disp([x' y'])

运行结果：

[ 2, 408488074749405/4503599627370496]

[ 3/2, -4481036472577419/9007199254740992]

[ 7/4, -1053779023151395/4503599627370496]

[ 15/8, -712341393175443/9007199254740992]

[ 31/16, 8975041611503/2251799813685248]

[ 61/32, -85593294866561/2251799813685248]

[ 123/64, -154268929443443/9007199254740992]

[ 247/128, -7430218095237/1125899906842624]

[ 495/256, -11835035444387/9007199254740992]

[ 991/512, 93879030099/70368744177664]

[ 1981/1024, 10840787111/1125899906842624]

[ 3961/2048, -5875158237047/9007199254740992]

[ 7923/4096, -723616715653/2251799813685248]

[ 15847/8192, -701966501541/4503599627370496]

[ 31695/16384, -164654758197/2251799813685248]

（2）运行程序：

a=0.1;b=1.5;k=0;

y1=a*sin(a)-1;

while(b-a)>0.01

k=k+1;

x0=(a+b)/2;x(k)=x0;

y0=x0 *sin(x0)-1;y(k)=y0;

if y0*y1<0

b=x0;

else

a=x0;

y1=y0;

end

disp([x' y'])

运行结果：

[ 4/5, -3838103856873717/9007199254740992]

[ 23/20, 55933053762297/1125899906842624]

[ 39/40, -1738305320249353/9007199254740992]

[ 17/16, -323478390340705/4503599627370496]

[ 177/160, -98943562990273/9007199254740992]

[ 361/320, 21826383383843/1125899906842624]

[ 143/128, 18951300402293/4503599627370496]

[ 1423/1280, -7626403754673/2251799813685248]

[ 495/256, -11835035444387/9007199254740992]

[ 991/512, 93879030099/70368744177664]

[ 1981/1024, 10840787111/1125899906842624]

[ 3961/2048, -5875158237047/9007199254740992]

[ 7923/4096, -723616715653/2251799813685248]

[ 15847/8192, -701966501541/4503599627370496]

[ 31695/16384, -164654758197/2251799813685248]

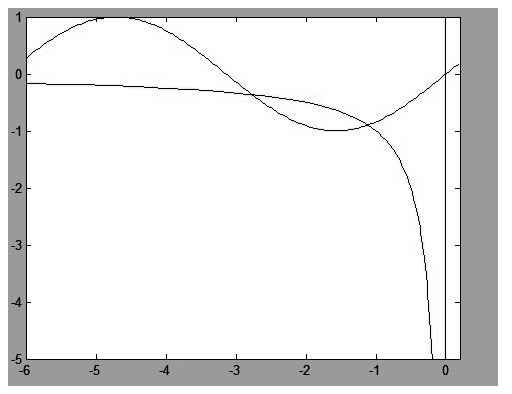
7.2方程xsin x=1的根实际上是两个函数y₁(x)=sin x,y₂(x)=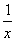的交点，用计算机绘出两个函数在区间[0.2，6]的图形如下，观察图形，分析它们的交点分布规律及特点，试写出方程的全部实根所在的隔根区间，并给出每一根的近似值。用计算机绘出区间[-6，0.2]上两个函数的图形，观察交点所在位置验证你的分析结果。

解：1，运行程序：

function [x,k]=ntf(fun,dfun,x0,eps,N)

if nargin<5

N=500;

end

if nargin<4

eps=1e-5;

end

k=1;

while k<N

x=x0-feval(fun,x0)/feval(dfun,x0);

if abs(x-x0)<eps

break;

end

x0=x;k=k+1;

end

if k==N

warning('已迭代次数上限');

end

format long

fun=inline('x*sin(x)-1');

dfun=inline('sin(x)+x*cos(x)');

[x,k]=ntf(fun,dfun,1,1e-8)

format long

fun=inline('x*sin(x)-1');

dfun=inline('sin(x)+x*cos(x)');

[x,k]=ntf(fun,dfun,1,1e-8)

运行结果：

（1）x =

1.114157140871930

k =

（2）x =

2.772604708265991

k =

2，画图验证

运行程序：

x=[-6:0.01*pi:0.2];

plot(x,sin(x))

hold on

syms t

fplot('1/t',[-6,0.2 -5 1])

实验八

8.1分别用直接法、雅可比迭代法、赛德尔迭代法求解线性方程组AX=b。

（1），

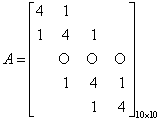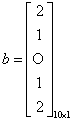
（2），

解：（1）a=ones(9);

c=4*ones(10);

A=diag(diag(c))+diag(diag(a),1)+diag(diag(a),-1);

b=[2;1;1;1;1;1;1;1;1;2];

B=[A,b]；

直接法

A\b

ans =

0.479271991911021

0.082912032355915

0.189079878665319

0.160768452982811

0.167846309403438

0.160768452982811

0.189079878665319

0.082912032355915

0.479271991911021

Jacobi法

Jocobi.m文件

function Jacobi(A,b,X0,P,error,max1)

[n n]=size(A);

X=zeros(n,1);

for k=1:max1

for j=1:n

X(j)=(b(j)-A(j,[1:j-1,j+1:n])*X0([1:j-1,j+1:n]))/A(j,j);

end

errX=norm(X-X0,P);

X0=X;X1=A\b;

if(errX<error)

disp('gvgfvgvg')

return

end

if(errX>=error)

disp('fgjsdj')

end

x0=[0;0;0;0;0;0;0;0;0;0];

Jacobi(A,b,x0,inf,0.001,100);

X =

0.479339599609375

0.083126068115234

0.189273834228516

0.161083221435547

0.168136596679688

0.161083221435547

0.189273834228516

0.083126068115234

0.479339599609375

Gauss-Seidel法

GS.m文件

function GS(A,b,X0,p,error,max1)

[n n]=size(A);

X=zeros(n,1);

for k=1:max1

for j=1:n

XX=0;

for i=1:n

if i<j

XX=XX+A(j,i)*X(i);

end

if i>j

XX=XX+A(j,i)*X0(i);

end

X(j)=(b(j)-XX)/A(j,j);

end

errX=norm(X-X0,p);

X0=X;X1=A\b;

if (errX<error)

disp('fgdfgh')

return

end

if(errX>=error)

disp('fghdgh')

end

x0=[0;0;0;0;0;0;0;0;0;0];

GS(A,b,x0,inf,0.001,100）；

X =

0.479258537292480

0.082895755767822

0.189098805189133

0.160642772912979

0.168022973462939

0.167701403144747

0.160854891291820

0.189039459481137

0.082926839553693

0.479268290111577

（2）b=[1;zeros(19,1)];

a=ones(18);

c=-2*ones(19);

d=5*ones(20);

A=diag(diag(d))+diag(diag(c),1)+diag(diag(a),2)+diag(diag(c),-1)+diag(diag(a),-2);

直接法

A\b

ans =

0.242121373548085

0.094391354624679

-0.021824158491067

-0.031362343009361

-0.006942557862112

0.004886927715767

0.003586117214438

0.000214823135181

-0.000784526508185

-0.000357861979163

0.000050437638520

0.000106309021306

0.000029232399870

-0.000014343050585

-0.000012667696430

-0.000001464361499

0.000002491258113

0.000001311981447

-0.000000093354238

-0.000000299737984

Jacobi法

x0=zeros(20,1);

Jacobi(A,b,x0,inf,0.001,100);

X =

1.0e+004 *

-0.282108278571715

0.482046406301265

-0.691953755956788

0.881266942075170

-1.052917666958734

1.201300209540189

-1.323751707356039

1.417537614867594

-1.480729230135441

1.512024114086328

-1.510826617470714

1.477238795829799

-1.412052361535888

1.316740113244093

-1.193359966404892

1.044725887301585

-0.873531574715016

0.685309155022675

-0.477119828561115

0.279134060154729

Gauss-Seidel法

GS(A,b,x0,inf,0.001,100)

X =

0.242291716096000

0.094772508426240

-0.021622113173504

-0.031486093950976

-0.007147457511424

0.004823645877699

0.003646069302467

0.000276912358545

-0.000775064735627

-0.000377224589581

0.000036657163528

0.000106214002021

0.000034034876168

-0.000011898463693

-0.000013058584947

-0.000002452084524

0.000002141863702

0.000001452223072

0.000000069366020

-0.000000262698207

相关推荐

数值分析课程设计报告

专栏推荐