实验5  FFT算法的应用

实验目的：加深对离散信号的DFT的理解及其FFT算法的运用。

实验原理：N点序列的DFT和IDFT变换定义式如下：

，

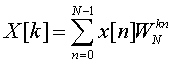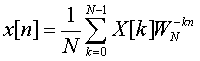
 利用旋转因子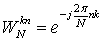具有周期性，可以得到快速算法（FFT）。

  在MATLAB中，可以用函数X=fft（x，N）和x=ifft（X，N）计算N点序列的DFT正、反变换。

实验内容：

2N点实数序列

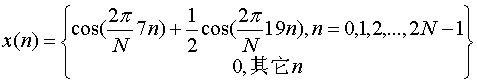
N=64。用一个64点的复数FFT程序，一次算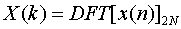出，并绘出。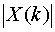

（2）已知某序列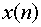在单位圆上的N=64等分样点的Z变换为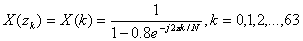。用N点IFFT程序计算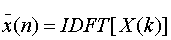，绘出和。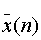

实验要求：利用MATLAB编程完成计算，绘出相应图形。并与理论计算相比较，说明实验结果的原因。

实验步骤：

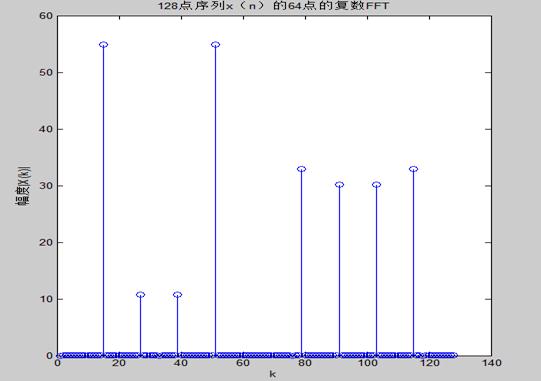
2N点实数序列x（n）的64点的复数FFT：

>> k=0:N-1;

>> n1=2*n;

>> n2=2*n-1;

>> x1=cos(2*pi*7*n1/N)+1/2*cos(2*pi*19*n1/N);

>> x2=cos(2*pi*7*n2/N)+1/2*cos(2*pi*19*n2/N);

>> XK1=fft(x1,64);

>> XK2=fft(x2,64);

>> XK11=XK1+(exp(-j*2*pi*k/N)).*XK2;

>> XK22=XK1-(exp(-j*2*pi*k/N)).*XK2;

>> XK11=[zeros(1,N),XK11];

>> XK22=[XK22,zeros(1,N)];

>> Xk=XK11+XK22;

>> k=0:1:2*N;

>> mag=abs(Xk);

>> stem(mag);

>> xlabel('k');

>> ylabel('幅度|X(k)|');

>> title('128点序列x（n）的64点的复数FFT');

>> 

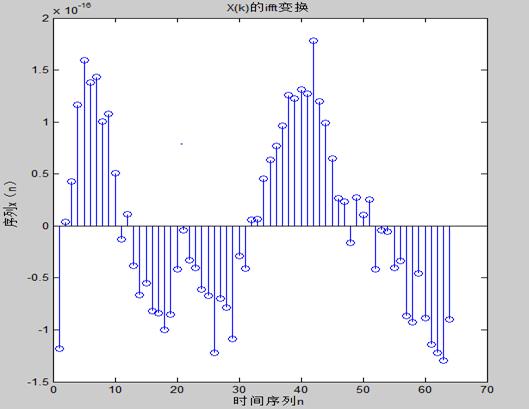
 (2) X(k)的N点IFFT:

>> N=64;

>> n=0:N-1;

>> Xk=1./(1-0.8.*exp(-2*pi*j*n/N));

>> xn=ifft(Xk,N);

>> stem(xn);

>> xlabel('时间序列n');

>> ylabel('序列x（n）');

>> title('X(k)的ifft变换');

>> 

 

第二篇：数字信号处理,实验,Matlab实验FFT算法实现

实验二  应用FFT对信号进行频谱分析

一、实验目的

   1、加深对离散信号的DTFT和DFT的及其相互关系的理解。

   2、在理论学习的基础上，通过本次实验，加深对快速傅里叶变换的理解，熟悉FFT算法极其程序的编写。

   3、熟悉应用FFT对典型信号进行频谱分析的方法。

   4、了解应用FFT进行信号频谱分析过程中可能出现的问题，以便在实际中正确应用FFT。

二、实验原理和方法

         一个连续信号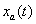的频谱可以用它的傅里叶变换表示

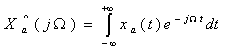                                           （2—1）

         如果对该信号进行理想采样，可以得到采样序列：

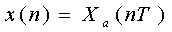                                                   （2—2）

         同样可以对该序列进行Z变换，其中T为采样周期

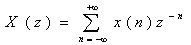                                                （2—3）

         当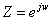得时候，我们就得到了序列的傅里叶变换

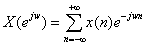                                                      （2—4）

         其中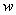称为数字频率，它和模拟频域的关系为

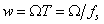                                                            （2—5）

 式中的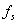是采样频率，上式说明数字频率是模拟频率对采样频率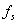的归一化。同模拟域的情况相似，数字频率代表了序列值变化的速率，而序列的傅里叶变换称为序列的频谱。序列的傅里叶变换和对应的采样信号频谱具有下式的对应关系 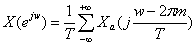：      （2—6）

     即序列的频谱是采样信号频谱的周期延拓。从式（2—6）可以看出，只要分析采样序列的频谱，就可以得到相应的连续信号的频谱。注意：这里的信号必须是带限信号，采样也必须满足Nyquist定理。

     在各种信号序列中 ，有限长序列在数字信号处理中占有很重要的地位。无限长的序列也往往可以用有限长序列来逼近。对于有限长的序列我们可以使用离散傅里叶变换（DFT），这一变换可以很好的放映序列的频域特性，并且容易利用快速算法在计算机上实现当序列的长度是N时，我们定义离散傅里叶变化为：

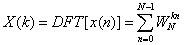                                                 （2—7）

其中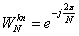，，它的反变换定义为：

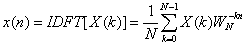                                        （2—8）

根据式（2—3）和（2—7）令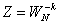，则有

                                        （2—9）

可以得到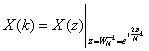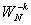，是Z平面单位圆上幅角为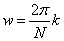的点，就是见单位圆进行N等分以后第K个点。所以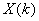，是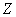变换在单位圆上的等距采样，或者说是序列傅里叶变换的等距采样。时域采样在满足Nyquist定理时，就不会发生频谱混淆；同样地，在频率域进行采样的时候，只要采样间隔足够小，也不会发生时域序列混淆。

     DFT时对序列傅里叶变换的等距采样，因此可以用于序列的频谱分析。在运用DFT进行频谱分析的时候可能有三种误差，分析如下：

   （1）混淆现象

       从式（2—6）中可以看出，序列的频谱是采样信号频谱的周期延拓，周期是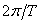，因此当采样速率不满足Nyquist定理，即采样频率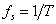小于两倍的信号（这里指的是实信号）频率时，经过采样就会发生频谱混淆。这导致采样后的信号序列频谱不能真实的反映原信号的频谱。所以，在利用DFT分析连续信号频谱的时候，必须注意这一问题。这就告诉我们，在确定信号的采样频率之前，需要对频谱的性质有所了解。在一般的情况下，为了保证高于折叠频率的分量不会出现，在采样之前，先用低通模拟滤波器对信号进行滤波。

（2）泄露现象

      实际中的信号序列往往很长，甚至是无线长序列。为了方便，我们往往用截短的序列来近似它们，这样可以使用较短的DFT来对信号进行频谱分析。这种截短等价于给原始信号序列乘以一个矩形窗函数，而矩形窗函数的频谱不是有限带宽的，从而它和原信号的频谱进行卷积以后会扩展原信号的频谱。值得一提的是，泄漏时不能和混淆完全分离的，因为泄漏导致频谱的扩展，从而造成混淆。为了减小泄漏的影响，可以选择是党的窗函数使频谱的扩散减小到最小。

（3）栅栏效应

         因为DFT是对单位圆上Z变换的均匀采样，所以它不可能将频谱视为一个连续函数。这样就产生了栅栏效应，从某种角度来看，用DFT来观看频谱就好像通过一个栅栏来观看一幅景象，只能在离散点上看到真实的频谱。这样的话就会有一些频谱的峰点或谷点被“栅栏”挡住，不能被我们观察到。减小栅栏效应的一个方法是在原序列的末端补一些零值，从而变动DFT的点数。这种方法的实质是人为地改变了对真是频谱采样的点数和位置，相当于搬动了“栅栏”的位置，从而使得原来被挡住的一些峰点或谷点显露出来。注意，这时候每根谱线对应的频率和原来的已经不相同了。

       从上面的分析过程可以看出，DFT可以用于信号的频谱分析，但必须注意可能产生的误差，在应用过程中要尽可能减小和消除这些误差的影响。

       快速傅里叶变换FFT并不是与DFT不相同的另一种变换，而是为了减少DFT运算次数的一种快速算法。它是对变换式（2—7）进行一次次的分解，使其成为若干小数点DFT的组合，从而减小运算量。常用的FFT是以2为基数，其长度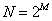。它的运算效率高，程序比较简单，使用也十分菲娜改变。当需要进行变换的序列的长度不是2的整数次方的时候，为了使用以2为基的FFT，可以用末尾补零的方法，使其长度延长至2的整数次方。IFFT一般可以通过FFT程序来完成，比较式（2—7）和（2—8），只要对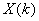取共轭，进行FFT运算，然后再取其共轭，并乘以因子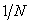，就可以完成IFFT。

三、实验内容及步骤

  （一）编制实验用主程序及相应子程序

1、在实验之前，认真复习DFT和FFT有关的知识，阅读本实验原理与方法和实验附录部分中和本实验有关的子程序，掌握子程序的原理并学习调用方法。

2、编制信号产生子程序及本实验的频谱分析主程序。试验中需要用到的基本信号包括：

（1）高斯序列：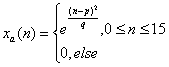

（2）衰减正弦序列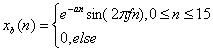

（3）三角波序列，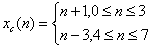

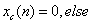
（4）反三角序列，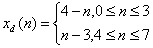

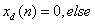
（二）上机实验内容

  1、观察高斯序列的时域和频域特性

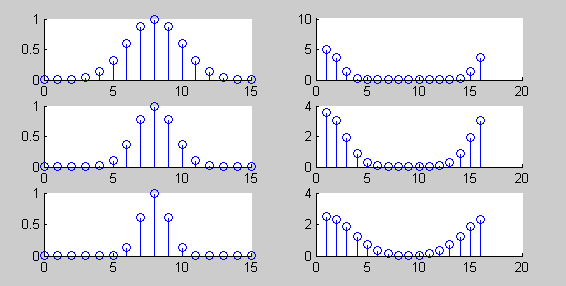
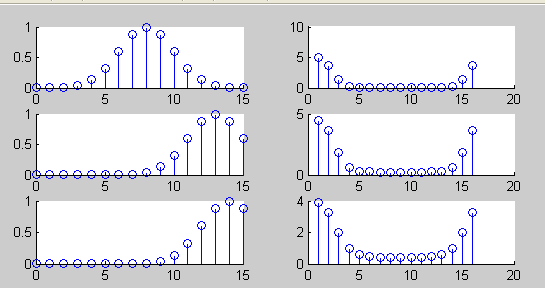
（1）固定信号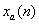的参数p=8,改变q的值，使q分别等于2，4，8。观察它们的时域和幅频特性，了解q取不同值的时候，对信号时域特性和幅频特性的影响。（2）固定q=8，改变p，使p分别等于8，13，14，观察参数p变化对信号序列时域及幅频特性的影响。注意p等于多少时，会发生明显的泄漏现象，绘制相应的食欲序列和幅频特性曲线。

1.高斯序列

>> n=0:15;  p=8;q=8;x=exp(-1*(n-p).^2/q);

>> subplot(3,2,2);stem(abs(fft(x))); subplot(3,2,1);stem(n,x);

>> p=8;q=4;x=exp(-1*(n-p).^2/q);

>> subplot(3,2,3);stem(n,x);subplot(3,2,4);stem(abs(fft(x)));

>> p=8;q=2;x=exp(-1*(n-p).^2/q);

>> subplot(3,2,5);stem(n,x); subplot(3,2,6);stem(abs(fft(x)));

>> n=0:15;p=8;q=8;x=exp(-1*(n-p).^2/q);

>> subplot(3,2,2);stem(abs(fft(x))); subplot(3,2,1);stem(n,x);

>> p=13;q=8;x=exp(-1*(n-p).^2/q);

>> subplot(3,2,3);stem(n,x); subplot(3,2,4);stem(abs(fft(x)));

>> p=14;q=8;x=exp(-1*(n-p).^2/q);

>> subplot(3,2,5);stem(n,x); subplot(3,2,6);stem(abs(fft(x)));

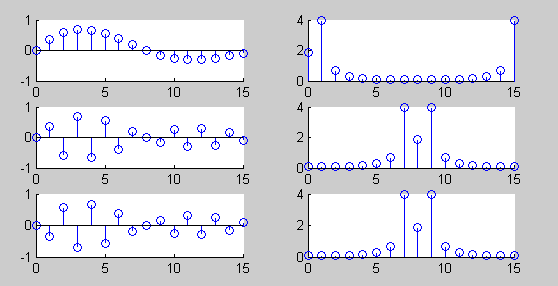
2.衰减正弦序列

>> n=0:15; a=0.1;f=0.0625; x=exp(-a*n).*sin(2*pi*f*n);

>> subplot(3,2,1);stem(n,x); subplot(3,2,2);stem(n,abs(fft(x)));

>> n=0:15; a=0.1;f=0.4375; x=exp(-a*n).*sin(2*pi*f*n);

>> subplot(3,2,3);stem(n,x); subplot(3,2,4);stem(n,abs(fft(x)));

>> n=0:15; a=0.1;f=0.5625; x=exp(-a*n).*sin(2*pi*f*n);

>> subplot(3,2,5);stem(n,x); subplot(3,2,6);stem(n,abs(fft(x)));

3．三角波序列

>> for i=1:4 x(i)=i; end  

>> for i=5:8 x(i)=9-i; end

>> subplot(2,1,1);stem(x); subplot(2,1,2);stem(abs(fft(x,16)))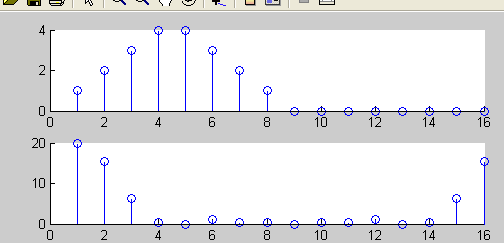

4.反三角序列

>> for i=1:4 x(i)=5-i; end

>> for i=5:8 x(i)=i-4; end

>> subplot(2,1,1);stem(x);subplot(2,1,2);stem(abs(fft(x,16)))

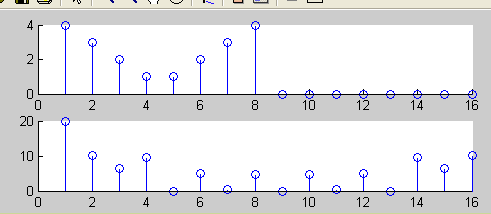
四、思考题

  1.实验中的信号序列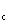x（n）和x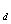(n),在单位圆上的Z变换频谱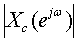和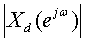

会相同吗？如果不同，你能说出哪一个低频分量更多一些吗？

答：不同

在单位圆上的Z变换频谱中，x_c(n)的低频分量比x_d(n)的多一些。

  2.对一个有限长序列进行离散傅里叶变换（DFT）,等价于将该序列周期延拓后进行傅里叶级数展开。因为DFS也只是取其中一个周期来运算，所以FFT在一定条件下也可以用分析周期信号序列。如果正弦信号sin(２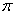ｆｎ)，ｆ＝０.1，用16点的FFT来做DFS运算，得到的频谱是信号本身的真实谱吗？

答：当N与进行FFT变换的点数K一样的时候，可以认为DFS与FFT的变换时相等的，这时我们可以用DFS来分析FFT。但是在N与K不相等的时候，DFS与FFT变换不等价。如上面所说得正弦信号sin(2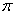fn)，f=0.1，用16点的FFT来做DFT运算，N=10而K=16 。用16 点FFT得到到的频谱不是真实信号的频谱。

五、实验总结：

   1．通过实验加深对离散信号的DTFT和DFT的及其相互关系的理解。

   2．在理论学习的基础上，通过本次实验，加深了对快速傅里叶变换的理解，熟悉了FFT算法极其程序的编写。

   3．了解了应用FFT进行信号频谱分析过程中可能出现的问题，以便在实际中正确应用FFT。