学习贝叶斯统计和经典统计的想法和心得
学习贝叶斯统计和经典估计理论的想法和心得
在应用数理统计课程中,李教授的系统讲解和耐心授课使我对应用数理统计这门课程有了一定了解,特别是对于数理统计的基本概念和相关统计思想认识更加深入,通过自主学习和查阅资料,我对贝叶斯统计和经典估计两种理论有了一些浅显的想法和心得。
在统计学发展历程中,经典统计方法在长时间占据着统计学的主导地位,但是,与经典统计的争论中逐渐发展起来的贝叶斯统计正在国外迅速发展并得到日益广泛的应用,可以说“二十一世纪的统计学是贝叶斯的时代”。 结合相关资料,针对两种统计理论的特点和区别,我认为贝叶斯统计和经典统计理论的分歧和区别主要在于以下两点。
第一,是否利用先验信息。由于产品的设计、生产都有一定的继承性,这样就存在许多相关产品的信息以及先验信息可以利用,贝叶斯统计学派认为利用这些先验信息不仅可以减少样本容量,而且在很多情况还可以提高统计精度;而经典统计学派忽略了这些信息。
第二,是否将参数e看成随机变量。贝叶斯统计学派的最基本的观点是:任一未知量e都可以看成随机变量,可以用一个概率分布去描述,这个分布就是先验分布。因为任一未知量都具有不确定性,而在表述不确定性时,概率与概率分布是最好的语言;相反,经典统计学派却把未知量e就简单看成一个未知参数,来对它进行统计推断。
贝叶斯统计学派与经典统计学派虽然有很大区别,但是它们各有优缺点,各有其适用的范围,作为学习者一定要博采众长,以获得一
种更适合解决实际问题的方法。而且,在不少情况下,二者得出的结论在形式上是相同的。
应用数理统计这门课程即将结束,在此,感谢李教授半年来对我们全体学员的谆谆教诲,在课上您是传授给我们知识的辛苦园丁,在课下又是与我们分享人生阅历的知心朋友,李教授的言行举止、敬业精神和人生态度是我们学习的榜样,50学时的课程让我受益匪浅、获益一生,再一次感谢李教授您的辛勤付出!
附:经典统计与贝叶斯统计的对比表
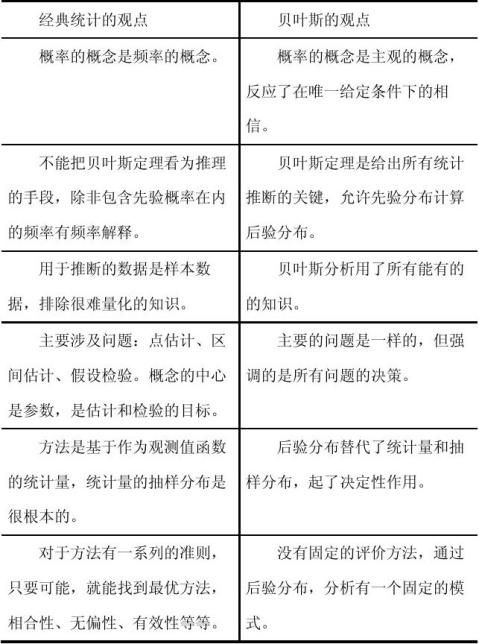
第二篇:贝叶斯统计简介
抛出一枚硬币,硬币落地,现在我不知道结果如何,问 是正面朝上还
是正面朝上还 是反面朝上?
是反面朝上?
答案有三个:A 正面朝上、B 反面朝上、C 正面朝上反面朝上的概率各占1/2
哪个正确?
经典统计学里面正确答案能是A或者B,只有在贝叶斯统计学里面答案C是才是被允许的
一次实验的结果在经典统计学里面被叫做样本点,是确定的。
那么为什么在贝叶斯统计学里面第三个的答案的说法是正确的呢?
关键在于贝叶斯学派关于随机变量的定义:任何一个未知量*都可以看做一个随机变量。
这也是贝叶斯学派最基本的观点,只要是未知的量都可以看做随机变量。
仅仅从这一个简单的例子就已经可以看到经典统计学派与贝叶斯统计学派的争议来了,其实两个学派在一些问题上的争论是相当深刻而激烈的,当然也有相同相通之处,在这里就不便展开详细的讨论了。就我本人还是比较倾向于贝叶斯学派的。
我们在回到上面的问题,看答案C正面朝上反面朝上的概率各占1/2,仔细想想这句话,实际上我们已经给出了未知量(本次实验结果)一个概率分布的描述。要么正面朝上要么反面朝上,概率各占1/2,这个概率分布被叫做先验分布。先验分布是指根据先验信息所给出的随机变量的分布,这里的先验信息是指在抽样之前有关统计问题的一些信息。那么先验分布与经典统计学里面的概率分布有什么区别呢?在所要满足的条件上,如……是一致的,主要区别在与概率分布得到的途径上。经典统计学里概率及其分布的确定来自大量重复实验,与频率密切相关,由大数定律、中心极限定理这些基本定理做为理论基石而得来。特别强调的是经典统计学的概率分布包含了所有样
 本点,即所有可能的实验结果都要被包含进去。这是与贝叶斯统计学里的先验分布不同的地方,贝叶斯统计学的先验概率分布来自于过去的经验,这里之所以加上”过去的“三个字并且对其强调,是想告诉大家先验分布只考虑已出现的样本点,不是所有的样本点。并且可以由经验而来不必做大量的重复实验。在这一点上克服了经典统计学的一些局限性,使得我们的研究深入到那些不适宜或不能大量重复的随机现象中来。当然这也使先验分布带有的主观性色彩。关于这一点也是一个经典统计学与贝叶斯统计学的一个争议点,有很多深入的问题正在探讨中。在这里我们就不讨论了。
本点,即所有可能的实验结果都要被包含进去。这是与贝叶斯统计学里的先验分布不同的地方,贝叶斯统计学的先验概率分布来自于过去的经验,这里之所以加上”过去的“三个字并且对其强调,是想告诉大家先验分布只考虑已出现的样本点,不是所有的样本点。并且可以由经验而来不必做大量的重复实验。在这一点上克服了经典统计学的一些局限性,使得我们的研究深入到那些不适宜或不能大量重复的随机现象中来。当然这也使先验分布带有的主观性色彩。关于这一点也是一个经典统计学与贝叶斯统计学的一个争议点,有很多深入的问题正在探讨中。在这里我们就不讨论了。
若仅仅研究先验分布贝叶斯估计也就没大意思了,与先验分布对应的还有后验分布。我们先来看一下后验分布的定义,在样本 给定下
给定下 的条件分布被称为
的条件分布被称为 的后验分布。我们分析一下这句话,首先可以明白后验分布是一个条件分布,怎样的条件分布呢,在样本
的后验分布。我们分析一下这句话,首先可以明白后验分布是一个条件分布,怎样的条件分布呢,在样本 给定的条件下的条件分布,看来仍然是需要样本,在贝叶斯统计中的样本又是什么样子的呢?从贝叶斯观点看,样本
给定的条件下的条件分布,看来仍然是需要样本,在贝叶斯统计中的样本又是什么样子的呢?从贝叶斯观点看,样本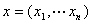 的产生主要分两步。首先设想从先验分布
的产生主要分两步。首先设想从先验分布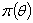 产生一个样本
产生一个样本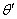 ,这一步是“老天爷”
,这一步是“老天爷”
做的,人们是看不见得,故用“设想”二字。第二步是从总体分布 产生一个样本
产生一个样本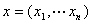 ,这个样本是具体的,人们能看的到的,此时样本
,这个样本是具体的,人们能看的到的,此时样本 发生的概率与如下联合密度函数成正比
发生的概率与如下联合密度函数成正比
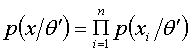
这个联合密度函数综合了总体信息与样本信息,常被称为似然函数,及为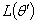 .由于
.由于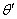 是设想出来的,他仍然是未知的,它是按先验分布
是设想出来的,他仍然是未知的,它是按先验分布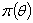 而产生的,要把先验分布进行综合,不能只考虑
而产生的,要把先验分布进行综合,不能只考虑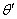 ,而应对
,而应对
的所有可能加以考虑。这样一来就有了样本 与参数
与参数 的联合分布
的联合分布
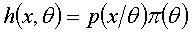
把先验信息,总体信息,样本信息都综合进去了。
我们在是件形式初等概率中已经学过贝叶斯公式的事件形式
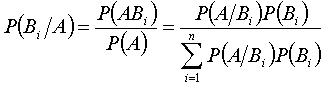
根据贝叶斯公式我们也可把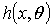 做如下分解
做如下分解
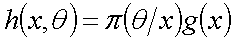
这里 是
是 的边缘分布函数,与
的边缘分布函数,与 无关,不含有
无关,不含有 的任何信息。
的任何信息。
在 是离散型随机变量时,
是离散型随机变量时,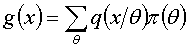 ;
;
在是连续型随机变量时,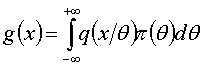 ;
;
这样我们就可以得到条件分布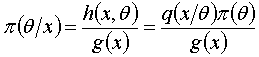
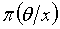 就是给定样本
就是给定样本 下,
下, 的条件分布了,也即
的条件分布了,也即 的后验分布。
的后验分布。
可以说后验分布是对先验分布的调整,它是集中了总体,样本和先验等三种信息中有关 的一切信息后的结果。
的一切信息后的结果。
为了更好的理解后验分布我们来看一个例子
例1:为提高某产品的质量,公司经理考虑增加投资来改进生产设备,预计需投资90万元,但从投资效果上看下属两个部门有两种意见:
 :改进生产设备后,高质量产品可占90%
:改进生产设备后,高质量产品可占90%
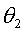 :改进生产设备后,高质量产品可占70%
:改进生产设备后,高质量产品可占70%
经理当然希望 发生,但根据两部门过去意见被采纳的情况,经理认为40%第一个部门是可信度的,60%第二个部门是可信度,即随机变量投资结果过
发生,但根据两部门过去意见被采纳的情况,经理认为40%第一个部门是可信度的,60%第二个部门是可信度,即随机变量投资结果过 的先验分布列为:
的先验分布列为: ;
;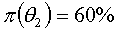
这是经理的主管意见,经理不想仅用过去的经验来决策此事,想慎重一些,通过小规模实验,观察其结果后再定。为此做了一项实验,实验结果(记为A)如下:
A:试制五个产品,全是高质量产品。
经理很高兴,希望通过这次结果来修正他原来对 和
和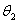 的看法。下面我们分别来求一下
的看法。下面我们分别来求一下 和
和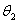 的后验概率。
的后验概率。
如今已有了 和
和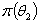 .还需要条件概率
.还需要条件概率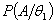 和
和 ,这可根据二项分布算的,
,这可根据二项分布算的,
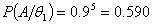 ;
;
由全概率公式可算的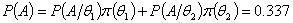
最后由后验分布公式可求得:
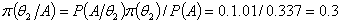
这表明,纪理根据实验A的信息调整了自己对投资结果的看法,把对 和
和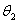 的信任度由0.4,和0.6分别调整到了0.7和0.3。后者综合了经理的主观概率和实验结果而获得,要比主观概率更具有吸引力,更贴近当前实际。当然经过实验A后经理对投资改进质量的兴趣更大了,但如果为了进一步保险起见可以把这次得到的后验分布列再一次作为先验分布在做实验验证,结果将更贴近实际。
的信任度由0.4,和0.6分别调整到了0.7和0.3。后者综合了经理的主观概率和实验结果而获得,要比主观概率更具有吸引力,更贴近当前实际。当然经过实验A后经理对投资改进质量的兴趣更大了,但如果为了进一步保险起见可以把这次得到的后验分布列再一次作为先验分布在做实验验证,结果将更贴近实际。
从上面这个例子中我们初步体验到了后验的求法,同时也能够看到贝叶斯统计的实用性。贝叶斯统计应用最做的是在决策方面,决策就是对一件事做出决定,它与统计推断的区别在于是否涉及到后果。统计推断依统计理论而进行,很少考虑到推断结果被使用时所带来的利润或造成的损失,这在决策中恰恰是不能忽略的。度量利损得失的尺度就是收益函数与损失函数,把收益函数和损失函数加入到贝叶斯推断就形成了贝叶斯决策论。
在这里首先明确几个概念
状态集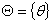 ,其中
,其中 表示自然界(或社会)可能出现的一种状态,所有可能的状态的集合组成状态集。
表示自然界(或社会)可能出现的一种状态,所有可能的状态的集合组成状态集。
行动集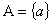 ,其中每一个元素表示人对自然界可能采取的一个行动。
,其中每一个元素表示人对自然界可能采取的一个行动。
损失函数 ,在一个决策问题中假设状态集为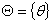 ,行动集为
,行动集为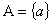 ,定义在
,定义在 上的二元函数
上的二元函数 称为损失函数,假如它能表示在自然界(或社会)处于状态
称为损失函数,假如它能表示在自然界(或社会)处于状态 ,而人们采取行动
,而人们采取行动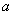 对人们引起的(经济的)损失。
对人们引起的(经济的)损失。
决策函数:在给定的贝叶斯决策问题中,从样本空间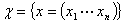 到行动集
到行动集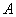 上的一个映射
上的一个映射 称为该决策问题的一个决策函数。
称为该决策问题的一个决策函数。
状态集,行动集,损失函数是构成一个决策问题必不可少的三个要素。
风险函数:评价T的优劣标准用平均损失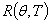 ,即
,即

称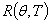 为T在
为T在 处的风险函数
处的风险函数
后验风险:损失函数 对后验分布的期望称为后验风险
对后验分布的期望称为后验风险
决策空间:设随机变量X的概率函数或概率密度函数为 ,其中
,其中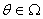 未知。对参数
未知。对参数 采取的所有“行动”(估计)组成的集合称为决策空间,记为A,在一般问题中,A是实数集且可测。
采取的所有“行动”(估计)组成的集合称为决策空间,记为A,在一般问题中,A是实数集且可测。
有了上面的基础,我们就可以讨论贝叶斯估计量了,为了简便起见,在这里假设X的分布和 的分布均为连续型。贝叶斯估计的基本思想就是选择一个估计值
的分布均为连续型。贝叶斯估计的基本思想就是选择一个估计值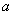 ,使得平均损失最小,即使
,使得平均损失最小,即使
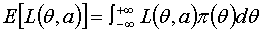
最小。
我们知道,后验分布是对先验分布的调整,在获得了一组样本的观测值之后,我们用 的后验概率密度函数
的后验概率密度函数 代替
代替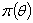 ,则上式写为:
,则上式写为:
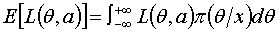
如果对样本的任何一组观测值,令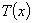 表示使上式最小的估计值,即
表示使上式最小的估计值,即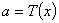 ,则称
,则称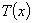 为
为 的贝叶斯估计量。
的贝叶斯估计量。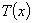 满足下式
满足下式
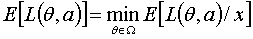
如果损失函数是平方形式,即 ,则其贝叶斯估计量为
,则其贝叶斯估计量为
证明:在平方损失函数 下,任何一个决策函数的后验风险为
下,任何一个决策函数的后验风险为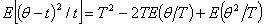
此后验分先的最小值仅在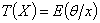 达到。
达到。
下面看看课本上的例题。
3.5节点估计的优良性
-
统计学学习心得
经过这一个学期对统计学的学习,深刻地了解到统计学和我们的生活息息相关,我们每一天都会遇到大量的统计问题,无论是走在大街上还是坐在电…
-
统计学个人心得
12级会计7班32120xx244谢翠欣在学习统计学之前,谈起统计我脑袋中就浮现出计数,一大堆枯燥的数字,还有一长串的数学计算式。…
-
统计学专题心得体会
统计学专题心得体会经过对统计学专题的学习,我对于统计学有了更加深入的了解。统计学运用的范围十分广泛,可以说几乎每个领域都会用到统计…
-
统计学学习心得
本学期我们专业开设了《统计学原理》课程,通过近一个学期的学习我们对统计学应用领域及其类型和基本概念有了一个基本的了解,掌握了数据的…
-
统计学心得
试验总结与心得经过了为期两天的统计学实验,主要通过EXCEL这个软件来完成这次的实验。首先掌握用EXCEL进行数据的搜集整理和显示…
-
概率论与数理统计心得体会
概率课感想与心得体会笛卡尔说过:“有一个颠扑不破的真理,那就是当我们不能确定什么是真的时候,我们就应该去探求什么是最最可能的。”随…
-
数理统计精品课程培训的心得体会
作为一名高校教师,自己在概率统计教学中积累了一些经验,也遇到了很多问题。通过这三天的培训,听了何老师认真细致的讲解,许多困惑渐渐清…
-
概率论与数理统计的学习心得
三四百年前在欧洲许多国家,贵族之间盛行赌博之风。掷骰子是他们常用的一种赌博方式。因骰子的形状为小正方体,当它被掷到桌面上时,每个面…
-
数理统计学习感想
数理统计学习感想学习了一学期的数理统计,我学会了如何在生活中运用所学的知识去解决一些问题。现实中常常存在这种情况,我们所掌握的数据…
-
《概率论与数理统计》课程学习心得
《概率论与数理统计》课程学习心得1004012033陈孝婕10计本3班有人说:“数学来源于生活,应用于生活。数学是有信息的,信息是…
-
概率论与数理统计学习心得
概率论与数理统计学习心得摘要:通过概率论与数理统计这门课的学习,我掌握了基本的概率论的知识,当然学习中也曾遇到过很多的问题。本文主…