论初等数论与小学数学的关系
论初等数论与小学数学的关系
——“同余”在小学数学教学中的应用
姓名:胡燕尔 班级:070214 学号:15 刚翻开人教版大学本科小学教育专业教材《初等数论》的目录,许多在校本科小学教育专业的学生,包括我都存在这样的感觉,那就是觉得这些是再简单不过的内容:整除、质数与合数、最大公约数与最小公倍数、同余等等,这些内容在我们读小学的时候都已经学习过,似乎觉得没有必要再去研究,直到接触学习了这门课程,才扭转了我们的看法。
初等数论是小学教育专业,尤其是理科方向学生的必修专业课程,也是从事小学数学教学的老师的进修课程。其中包括整数的整除性、同余、同余方程、不定方程、不定方程、简单连分数几方面的知识。这些方面的内容在符合了小学数学教师应具有的教学思维外,也有利于学习者积累从事小学数学教育工作必备的能力与知识。
有人说:“数学是思维的体操,科学的王冠,数论是王冠上的明珠。”这颗明珠在小学数学中早已是熠熠闪光——我们小学所学习到的数论内容主要包含以下几类:
整除问题:(1)整除的性质;(2)数的整除特征 (小升初常考内容)
余数问题:(1)带余除式的运用 被除数=除数×商+余数.(余数总比除数小)
(2)同余的性质和运用
奇偶问题:(1)奇偶与加减运算;(2)奇偶与乘除运算
质数合数:重点是质因数的分解
约数倍数:(1)最大公约最小公倍两大定理 (2)约数个数决定法则 可见,初等数论的应用与小学数学教育事业是息息相关的。对于初等数论,我学到的也只是九牛一毛,谈不上有什么有建设性的问题,只能粗略地谈谈初等数论中的核心内容——同余,并通过其在初等数论在小学数学中的应用来说明两者的关系。
同余是由德国数学家高斯首先提出并系统地进行研究的,它是初等数论的核心部分。其中蕴含大量的数论所特有的思想、概念和方法,它的出现使数论成为一个独立的数学分支的标志。在这一内容中包括其性质,剩余类与剩余系,欧拉
定理和循环小数等几个知识点。在没接触初等数论学习之前,我们对同余这个概念很陌生,其实同余在我们小学数学学习,奥数中已经有了很深入的运用。在小学中主要体现在余数的运用上,余数是小学数学中的重要概念,也是数学竞赛的热门话题,其中有关概念多,方法性强。
在小学,关于余数问题我们知道:如果整数a除以正整数m,商为q,余数为r,则a=qm+r,其中q与r都是自然数,并且0≤r<m.而现在我们学的同余知识是:如果两个正整数a,b被非零自然数m除时所得的余数相同,a=qm+r,b=pm+r,那么就说a与b关于模m同余,记为a≡b(mod m).此时a与b的差能被m整除,记为a-b ≡0(mod m).因此同余问题常常转化为整除问题求解。
下面,我以一个例题来反应同余在小学数学教学中的应用:
例题、a除以5余1,b除以5余4,如果3a>b,那么3a-b除以5余几? 这道题目出现在小学奥数中,小学生一般的解答方法是:
方法一:凑数法。取a为6,取b为9,这样a.b满足了条件a除以5余1,b除以5余4,3a-b=9,9/5余数为4。
方法二、设a=5x+1 b=5y+4 3a-b=15x-5y-1=15x-5y-5+4=5(3x-y-1)+1 3a-b除以的余数是4 a=5x+1 (x为正的整数) b=5y+4( y为正的整数 ) (3a-b)/5 =(15x+3-5y-4)/5 =3x-y-1/5 =(3x-y-1)+4/5
根据x,y均为正的整数,并且3a>b,所以余数为4。
而在初等数论中的解法:
解:∵a≡1(mod5),
∴3a≡3(mod 5),
或者3a≡8(mod 5).(1)
又∵ b≡4(mod 5),(2)
∴(1)-(2)得:
3a-b≡8-4≡4(mod 5).
因此,3a-b除以5余4.
在小学生解法中我们可以看出,两种方法,尤其是第二种,都是以同余知识出发去处理问题,只是在形式表达上相对于大学里初等数论练习中较为简单化。在小学的奥数思维训练中,同余思想的应用更是数不胜数,如“抽屉原理”是同
余应用中最典型的例子,可以说,同余理论是近世代数中一个很重要的数学模型。除此之外,其他很多数学知识都涉及到了同余,比如像欧拉函数,它也是初等数论中的重要函数之一,在证明过程中就大量地体现了同余的思想。
学过初等数论的人应该都知道,小学数学和初等数论之间最大的不同在于小学数学在于如何应用定理、法则,而初等数论则要明白为什么这么应用。显然,初等数论是更为深层次的学习,在难度上有了一个跨越。那么数论部分在小学数学考试题型中占据什么地位呢?可以说,翻开任何一本数学辅导书,数论的题型都占据了显著的位置。有专家在小学各类数学竞赛中研究发现,直接运用数论知识解题的题目分值大概占据整张试卷总分的30%左右,而在竞赛的决赛试题中,这一分值比例更高。出题老师喜欢将数论题作为区分尖子生和普通学生的依据,这一部分学习的好坏将直接决定学生在选拔性考试中成绩的好坏。
综上所述,初等数论作为一门为小学教育专业的学生开设的课程,在培养学生扎实的数学基础之外,更多的是有利于师范生更好地将初等数论的理论灵活地应用于小学教育中,进一步培养科学的人生观、价值观。
第二篇:初等数论中蕴含的数学思想
初等数论中蕴含的数学思想
摘要:通过对初等数论中的某些问题的解决思路的总结概括,以及对其中重要定理或引理的证明过程的回顾,探讨了数论中蕴含的几类数学思想方法,即:转化、整体、配对、群论思想方法及整数矩阵在初等数论中的应用。
关键字:初等数论;数学思想方法;整除
Mathematical Thinking in Elementary Number Theory
Abstract: By elementary number theory problems in some of the ideas summed up. And we review the proof process of some important theorems or lemmas. It is discussed that several mathematics thought way in Elementary theory. That is, conversion, overall, matching materials, groups and group representations thinking method and integer matrix in the application of elementary number theory.
Key words: elementary theory ,mathematical way of thinking,division
数论,这门古老而又常新的学科既是典型的纯粹数学,又是日益得到广泛应用的新“应用数学”.
在数论中,初等数论是以整除理论为基础,研究整数性质和方程(组)整数解的一门数学学科,是一门古老的数学分支.它展示着近代数学中最典型、最基本的概念、思想、方法和技巧.目前,初等数论在计算机科学、代数编码、密码学、组合数学、计算方法等领域内得到了广泛的应用,成为计算机科学等相关专业不可缺少的数学基础.
数论的魅力在于它可以适合小孩到老人,只要有算术基础的人均可以研究数论.初等数论貌似简单,但真正掌握并非易事,它的内容严谨简洁,方法奇巧多变,其中蕴含了丰富的数学思想方法.本文以初等数论中重要的定理的证明为据,配以具体的数论问题,谈谈初等数论中蕴含的转化、整体、归纳、群论思想方法及整数矩阵在初等数论中的应用.
1 转化思想方法
转化是一种常用的数学思想方法.转化是指问题之间的相互转化,或者将问题的一种形式转化为另一种形式,或者把复杂问题转化成较简单问题、将陌生问题转化为已解决或熟悉的问题[1].通过恰当的化归转化不仅能够顺利地解决原问题,而且有助于培养学生科学的思维习惯.
整除是数论中的基本概念,此问题是数论中比较简单的一种类型.有时我们需要判断几个分式的和是一个整数,这样直接求其是整数比较困难,因而常常化为整除问题解决.
例1 证明对于任意整数 ,数
,数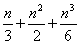 是整数.
是整数.
证明 
又由于两个连续整数的乘积是2的倍数,三个连续整数的乘积是3的倍数,并且 ,所以有
,所以有
 和
和
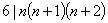
即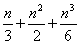 是整数.
是整数.
从历史上来看,不定方程问题的求解是推动数论发展的最主要课题.有的不定方程问题直接求解或证明比较困难,因而常常转化为整除问题解决.
例2(第35届美国中学数学竞赛题)满足联立方程
 的正整数
的正整数 的组数是()
的组数是()
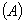 0
0  1
1 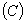 2
2  3
3  4
4
解(质因数分解法)由方程 得
得
 .
.
 ,
,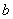 ,
, 为整数,
为整数, 且
且 .将
.将 和
和 代入方程
代入方程
得
 ,即
,即 ,
,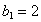 ,
, .从而得
.从而得 ,
, .故满足联立方程是正整数组
.故满足联立方程是正整数组 有两个,即
有两个,即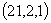 和
和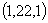 ,应选
,应选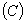 .
.
这说明数学问题上的许多问题,都可以转化为整除问题.另外,整除问题也可以转化为其它问题.我们知道同余理论是初等数论的核心,有时整除问题转化为同余问题解决,思路更清晰、自然、计算更简洁.
例3 试判断 能被3整除吗?
能被3整除吗?
解  ,
, ,
, ,
,

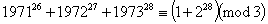
 ,
,

 不能被3整除.
不能被3整除.
2 整体化思想方法
Euler 定理[2]  ,
,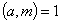 ,则
,则 .
.
这是初等数论的一个基本定理,有着广泛的应用.其证明如下:
若 是模
是模 的一个简化剩余系,则
的一个简化剩余系,则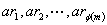 也是模
也是模 的一个简化剩余系,于是
的一个简化剩余系,于是 ,即证.
,即证.
Euler定理的证明虽然十分简单,但其中包含了初等数论中常用的一个解题方法,即“整体思想”. 整体化思想方法,就是把单个对象始终放在整体对象构成的系统中加以考虑,通过系统对象之间的整体联系或整体特征,寻求原问题的解决途径[3].
在解题过程中,常常运用这一种思路:以完全剩余系为例,即 及
及 ,
, ,
, ,
, 为模
为模 的两个完全剩余系,则
的两个完全剩余系,则 恰与
恰与 ,
, ,
, ,
, 中的某一数同余,于是
中的某一数同余,于是 与
与 同余,由此找到证明的途径.
同余,由此找到证明的途径.
例4 设 和
和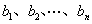 分别是模
分别是模
 的一组完全剩余系,且
的一组完全剩余系,且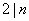 ,求证:
,求证: 不是模
不是模 的一组完全剩余系.
的一组完全剩余系.
证明 假设 ,
, 是模
是模 的一组完全剩余系.
的一组完全剩余系.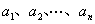 是模
是模 的一组完全剩余系,则:
的一组完全剩余系,则:

同理有: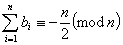 .
.
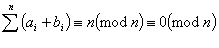 .
.
又 ,
, 也是模
也是模 的一组完全剩余系,则有:
的一组完全剩余系,则有:
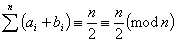 ,又
,又 ,矛盾!证毕.
,矛盾!证毕.
例5 设整数 ,证明:
,证明: ,即在数列
,即在数列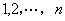 中,与
中,与 互素的正整数之和是
互素的正整数之和是 .
.
证明 设在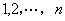 中与
中与 互素的
互素的 个整数是
个整数是 ,
,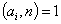
 则
则
 ,因此,集合
,因此,集合 与
与 都是由
都是由 中与
中与 互素的整数组成,即这两个集合中的元素完全相同,所以
互素的整数组成,即这两个集合中的元素完全相同,所以

从而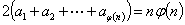
因此 ,即证.
,即证.
3 配对思想方法
配对思想方法,就是将整体对象中的满足某种特性的对象进行组合配对,再利用配对后的特性解决原问题[1].
定义[2] 欧拉函数 是定义在正整数集上的函数,
是定义在正整数集上的函数, 等于序列
等于序列
 中与
中与 互素的正整数的个数.
互素的正整数的个数.
定义[2] 在模 的每个互素剩余类
的每个互素剩余类
 中任取一数
中任取一数 ,则
,则
所有的数
 所组成的集,叫做模
所组成的集,叫做模 的一个简化
的一个简化
剩余系.
定义[2] 在 个与模
个与模 互素的剩余类中各取一个数,称这
互素的剩余类中各取一个数,称这 个数为模
个数为模
的简化剩余系.
例6 设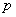 是素数,证明:
是素数,证明: .
.
证明 当 时结论显然成立,不妨设素数
时结论显然成立,不妨设素数 .
.
对于 中的每个整数
中的每个整数 ,都存在唯一的整数
,都存在唯一的整数 ,
, ,使得
,使得

因此,整数 可以两两配对使得上式
可以两两配对使得上式 成立,于是有
成立,于是有

从而
此题的结论称为Wilson定理,其证明过程蕴含了“配对”的思想方法.
例7 求证: ,
, ,
, ,
, ,
, ,
, ,
,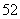 ,
, 是模
是模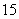 的简化剩余系.
的简化剩余系.
证明 在 中与15互素的数有
中与15互素的数有 个:
个: ,所以
,所以 .因此与模
.因此与模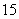 互素的剩余类为
互素的剩余类为 .又
.又 ,
,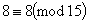 ,
, ,
,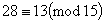 ,
, ,
, ,
, ,
, ,
, ,
, ,
,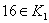 ,
, ,
, ,
, ,
,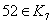 ,
,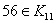 ,所以
,所以 ,
, ,
, ,
, ,
, ,
, ,
,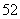 ,
, 是模
是模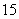 的简化剩余系.
的简化剩余系.
例如下面的简单事实都是配对的基础:
 若d是正整数
若d是正整数 的正因数,则
的正因数,则 与
与 同为正整数
同为正整数 的正因数.
的正因数.
 二次剩余定理的证明.
二次剩余定理的证明.
例8 若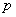 为素数,
为素数, ,证明
,证明 ,其中
,其中 是
是 对模
对模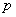 的Legendre符号.
的Legendre符号.
证明: ,
,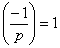 ,于是
,于是 .因此,
.因此, 与
与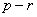 同为模
同为模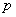 的平方剩余或同为平方非剩余.令
的平方剩余或同为平方非剩余.令 ,则对模p而言有
,则对模p而言有 个平方剩余及
个平方剩余及 个平方非剩余.据此,对任一
个平方非剩余.据此,对任一
 ,将
,将 与
与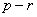 配对,则
配对,则 个平方剩余可配成
个平方剩余可配成 对,
对, 个平方非剩余也可配成
个平方非剩余也可配成 对,故
对,故
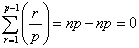 .
.
值得注意的是,配对思想方法实质上是通过配对把局部补成整体的一种方法,因此也可以说是整体化思想的一种变形.数论解题中运用整体化的思想方法较为普遍,体现了数论解题思维的灵活性,利用整体化思想方法或配对思想,可以另辟蹊径获得巧妙简捷的解(证)题效果.
4 群论思想方法
数论的问题以其抽象且难度大而著称,而抽象恰恰也是近世代数的最大特点.近世代数思想方法一直都被用到数论问题的处理中.下面我们通过对初等数论的定理的证明来介绍群论的思想方法在数论中的应用[4].
 定理 设
定理 设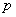 是一个素数且
是一个素数且 是一个不能被
是一个不能被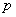 整除的自然数,那么
整除的自然数,那么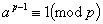 .
.
证明 考虑模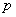 的非零剩余组成的乘法群
的非零剩余组成的乘法群 .若
.若 是一个不能被
是一个不能被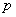 整除的自然数,则
整除的自然数,则 .所以
.所以 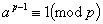 .
.
5 矩阵的思想方法
初等数论课本上,利用整数初等变换,仅研究了两个整数的最大公约数和最小公倍数的问题,略显不够深入.再此基础上,我们可以通过构造整数矩阵,一矩阵的整数的初等变换为工具,得到了求
 个整数的最大公约数与最小公倍数的方法[5].
个整数的最大公约数与最小公倍数的方法[5].
利用初等变换求整数的最大公约数
命题 设 ,则存在可逆矩阵
,则存在可逆矩阵 ,使得
,使得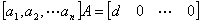
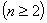 .
.
证明 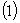 当
当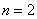 时,可设
时,可设 ,由辗转相除法知:
,由辗转相除法知:
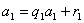 ,
,
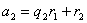 ,
,
……
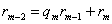 ,
,


于是,令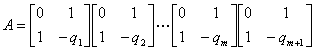
则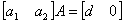 ,命题成立;
,命题成立;
 假定
假定
 时,命题成立.则当
时,命题成立.则当 时,由假定知,存在
时,由假定知,存在 阶可逆方阵
阶可逆方阵 ,使得:
,使得: ,其中
,其中 ,从而有
,从而有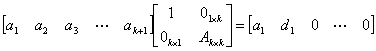
又由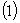 知,存在二阶可逆方阵
知,存在二阶可逆方阵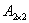 ,使得
,使得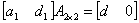 .
.
其中 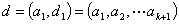 ,
,
于是令 ,则
,则
即当 时,命题成立;由归纳法原理知,当
时,命题成立;由归纳法原理知,当 时,命题成立.(证毕)
时,命题成立.(证毕)
推 论 设 , 为不全为0的整数,则存在
, 为不全为0的整数,则存在 上的
上的 阶可逆矩阵B,使
阶可逆矩阵B,使 .
.
且 是
是 的最大公因数,B是一些初等矩阵的乘积.
的最大公因数,B是一些初等矩阵的乘积.
B的求法如下:将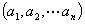 下面写一个
下面写一个 阶单位矩阵,构成一个
阶单位矩阵,构成一个 矩阵,再对
矩阵,再对
 施行初等变换,当
施行初等变换,当 的第一行变成
的第一行变成 时,则下面的单位阵变化成了
时,则下面的单位阵变化成了 .
.
即:
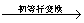

例9求40,38,72的最大公因数.
解 作矩阵
所以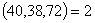
初等数论解题过程中除了以上探讨的整体化、配对、化归、群论思想方法,还涉及其他的思想方法(如:环论思想,构造思想,分类思想及模方法在素数判断中的应用等).值得注意的是,初等数论解(证)题往往是多种思想方法相互交织、渗透、化归的综合应用过程.
如:在例2中,首先是将问题化为 ,在
,在 ,
,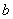 ,
, 均为整数的情况下,只有
均为整数的情况下,只有 ,进而简化了问题,再运用代入法解决该题.
,进而简化了问题,再运用代入法解决该题.
初等数论中蕴含了丰富的数学思想方法,其知识结构和数学思想方法形成一个经纬交织,融会贯通的知识网络,需要我们去挖掘、揭示.因此在初等数论的教学过程中,应充分利用教材和习题的教育功能,注重展示解决问题的思路、思维过程,体现解决问题策略与方法的多样性,引导沟通知识间的内在联系,突出问题的背景和思想方法的阐述,注重思想方法的总结、提炼,把数学知识和相关数学思想方法有机联系起来,使学生从整体上把握初等数论的理论体系,理解数学思想方法的内涵,开阔思维视野,健全认知结构.
参考文献
[1]王丹华,杨海文.初等数论中蕴涵的数学思想方法[J].井冈山学院学报.2007.04.13(4):11-13.
[2]张文鹏.初等数论[M].西安:陕西师范大学出版设,2007.4.(1): 54-56.
[3]王丹华,杨海文等.初等数论[M].北京:北京航空航天大学出版社,2008.3.(1):65-66.
[4]张清,唐再良.近世代数思想方法在数论中的应用[J].绵阳师范学院学报,2007,26
(5):12-14.
[5]陈碧琴.矩阵初等变换在初等数论中的应用[J].南通工学院学报.2004.3.3(1):01-04.
[6] 闵嗣鹤,严士健.初等数论[M].北京:高等教育出版社,2003.12.(3):08-15.
-
小学数学论文范文
小学数学论文范文小学数学生活化策略摘要小学数学不会自发产生与现实生活的联系运用数学知识和方法解决一些简单的实际问题需要采用切实可行…
-
小学数学教学论文范文
小学数学教学论文范文谈小学数学阅读能力的培养摘要人们常讲数学是思维的体操在这句话的误导下很多人只是把数学与思维联系起来认为数学只能…
-
小学数学教学论文范文[1]
小学数学课堂的预设与生成课堂教学活动是面对着不同个性的生命体它又是充满活力的生成的过程教学活动正是静态预设在课堂中动态生成的过程重…
-
小学数学论文范文
新课标下小学数学与生活的接轨新的一轮课程改革进一步促使数学生活化数学与生活进一步接轨是指从学生的已有经验出发让学生亲身经历将实际问…
-
小学数学论文范文:小学数学生活化策略
小学数学论文范文小学数学生活化策略摘要小学数学不会自发产生与现实生活的联系运用数学知识和方法解决一些简单的实际问题需要采用切实可行…
-
20xx年进出口企业年终总结
20xx年,**企业全体干部员工在实践中运用科学发展观,团结一心,克服困难,趁势而上,不断进取,确保全面完成20xx年企业的各项经…
-
20xx年医院护士上半年工作总结
光阴似箭!一晃眼,从我加入人民医院——救死扶伤的护士,工作已有半年多了。在过去半年里,在院领导、科主任及护士长的正确领导下,我认真…
-
初一班主任工作总结
时光飞逝,转眼之间一学期又过去了。今年当初一(156)班的班主任,这届初一学生学习习惯很差;另外,成绩、品德、纪律皆差。本学期在校…
-
二0一0年下学期历史教研组工作总结[1]
20xx一20xx年下学期历史教研组工作总结20xx年x月11丁景良一、指导思想:坚持科学发展观为指导,以“科研兴校”为宗旨,以抓…
-
工会半年检查总结
友谊街道工会上半年工作总结上半年,我友谊街道总工会在组建工会和发展会员工作中,严格按照旗总工会“两个普遍”要求,结合我街道实际情况…