初等数论教案5
第九节 自然数的性质
教学目的:1、掌握第一、第二数学归纳法;
2、掌握最小自然数原理;
3、掌握并会应用抽屉原理.
教学重点:应用最小自然数原理以及抽屉原理.
教学过程
1、归纳原理 设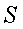 是
是 的一个子集,满足条件:
的一个子集,满足条件:
(1) 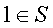 ; (2) 如果
; (2) 如果 ,则
,则 . 那么
. 那么 .
.
2、数学归纳法 设 是关于自然数
是关于自然数 的一种性质或命题. 如果 (1) 当
的一种性质或命题. 如果 (1) 当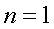 时,
时, 成立;
成立;
(2) 由 成立必可推出
成立必可推出 成立,
成立,
那么, 对所有自然数
对所有自然数 都成立.
都成立.
证明:设使 成立的所有自然数
成立的所有自然数 所组成的集合是
所组成的集合是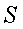 ,则
,则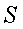 是
是 的一个子集. 由条件(1) 知
的一个子集. 由条件(1) 知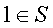 ;由条件 (2)知若
;由条件 (2)知若 ,则
,则 ,那么
,那么 .
.
3、最小自然数原理 设 是
是 的一个非空子集. 那么,必有
的一个非空子集. 那么,必有 ,使得对所有
,使得对所有 ,都有
,都有 ,即
,即 是
是 中的最小自然数.
中的最小自然数.
4、第二数学归纳法设 是关于自然数
是关于自然数 的一种性质或命题. 如果
的一种性质或命题. 如果
(1) 当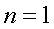 时,
时, 成立;
成立;
(2) 设 ,若对所有自然数
,若对所有自然数 ,
, 成立,必可推出
成立,必可推出 成立,那么,
成立,那么, 对所有自然数
对所有自然数 都成立.
都成立.
5、抽屉原理 把 件东西任意放入
件东西任意放入 只抽屉里,那么至少有一个抽屉里有两件东西.
只抽屉里,那么至少有一个抽屉里有两件东西.
把 件东西放入
件东西放入 个抽屉里,那么至少有一个抽屉里至少有
个抽屉里,那么至少有一个抽屉里至少有 +1件东西.
+1件东西.
无穷件东西,把它们放在有限多个抽屉里,那么至少有一个抽屉里含无穷件东西.
例1、证明:若 表示第
表示第 个素数,则
个素数,则 .
.
证明:略.
例2、在边长为1的正方形内任意放置5个点,试证:其中必有两个点,它们之间的距离不大于 .
.

证明:将边长为1的正方形划分成如图所示的四个边长为 的小正方形,则每个小正方形中任意两点间的距离不大于
的小正方形,则每个小正方形中任意两点间的距离不大于 ,据抽屉原理:5个点放入四个正方形中,其中至少有一个正方形中至少有2个点,则这两个点间的距离不大于
,据抽屉原理:5个点放入四个正方形中,其中至少有一个正方形中至少有2个点,则这两个点间的距离不大于 .
.
例3、求证:任给五个整数,必能从中选出三个,使得它们的和能被3整除.
证明:因为任意一个整数被3除的余数只能是0、1、2,若任给的5个整数被3除的余数中0、1、2都出现,则余数为0、1、2的三个整数之和能被3整除.若5个数被3除的余数只出现0、1、2中的两个,则据抽屉原理知:必有3个整数的余数相同,而余数相同的3个数之和能被3整除.故任给五个整数,必能从中选出三个,使得它们的和能被3整除.
例4、证明:在全世界所有人中任选六个人,其中一定有三个人,他们之间或者互相认识,或者互相不认识.
证明:略.
例5、平面上有1987个点,任取三个点中都有两点的距离小于1. 求证:存在半径为1的圆,它至少盖住994个点.
证明:在所给的1987个点中任选一点,记为A,以A为圆心作一个半径为1的圆,若其余的1986个点都在圆A内,则结论成立.否则,在圆A外的点中任一点,记为B,以B为圆心作一个半径为1的圆,则除去A、B之外的其余1985个点必在圆A或圆B内,否则,至少存在一点C在圆A或圆B的外部,则A、B、C三点任两点间的距离均大于1,与条件矛盾,所以除去A、B之外的其余1985个点必在圆A或圆B内.据抽屉原理:必有一个圆内至少有 个点,加上圆心共994个点. 知结论成立.
个点,加上圆心共994个点. 知结论成立.
6、小结
7、作业 P26:32、34、39、41
第二篇:初等数论教案
第一章 整除理论
整除性理论是初等数论的基础。本章要介绍带余数除法,辗转相除法,最大公约数,最小公倍数,算术基本定理以及它们的一些应用。
第一节 数的整除性
定义1 设a,b是整数,b¹ 0,如果存在整数c,使得
a = bc
成立,则称a被b整除,a是b的倍数,b是a的约数(因数或除数),并且使用记号b½a;如果不存在整数c使得a = bc成立,则称a不被b整除,记为b a。
a。
显然每个非零整数a都有约数±1,±a,称这四个数为a的平凡约数,a的另外的约数称为非平凡约数。
被2整除的整数称为偶数,不被2整除的整数称为奇数。
定理1 下面的结论成立:
(ⅰ) a½bÛ±a½±b;
(ⅱ) a½b,b½cÞa½c;
(ⅲ) b½ai,i = 1, 2, L, kÞb½a1x1+a2x2+L+akxk,此处xi(i = 1, 2, L, k)是任意的整数;
(ⅳ) b½a Þbc½ac,此处c是任意的非零整数;
(ⅴ) b½a,a¹ 0 Þ |b| £ |a|;b½a且|a| < |b| Þa = 0。
证明 留作习题。
定义2 若整数a¹ 0,±1,并且只有约数±1和±a,则称a是素数(或质数);否则称a为合数。
以后在本书中若无特别说明,素数总是指正素数。
定理2 任何大于1的整数a都至少有一个素约数。
证明 若a是素数,则定理是显然的。
若a不是素数,那么它有两个以上的正的非平凡约数,设它们是d1, d2, L, dk 。不妨设d1是其中最小的。若d1不是素数,则存在e1 > 1,e2 > 1,使得d1 = e1e2,因此,e1和e2也是a的正的非平凡约数。这与d1的最小性矛盾。所以d1是素数。证毕。
推论 任何大于1的合数a必有一个不超过 的素约数。
的素约数。
证明 使用定理2中的记号,有a = d1d2,其中d1 > 1是最小的素约数,所以d12£a。证毕。
例1 设r是正奇数,证明:对任意的正整数n,有
n+ 2 1r+ 2r+L+n r。
1r+ 2r+L+n r。
解 对于任意的正整数a,b以及正奇数k,有
ak+bk = (a+b)(ak- 1-ak- 2b+ak- 3b2-L+bk- 1) = (a+b)q,
其中q是整数。记s = 1r+ 2r+L+n r,则
2s = 2 + (2r+n r) + (3r+ (n- 1)r) +L+ (n r+ 2r) = 2 + (n+ 2)Q,
其中Q是整数。若n+ 2½s,由上式知n+ 2½2,因为n+ 2 > 2,这是不可能的,所以n+ 2 s。
s。
例2 设A = { d1, d2, L, dk }是n的所有约数的集合,则
B =
也是n的所有约数的集合。
解 由以下三点理由可以证得结论:
(ⅰ) A和B的元素个数相同;
(ⅱ) 若diÎA,即di½n,则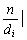 n,反之亦然;
n,反之亦然;
(ⅲ) 若di¹dj,则 。
。
例3 以d(n)表示n的正约数的个数,例如:d(1) = 1,d(2) = 2,d(3) = 2,d(4) = 3,L。问:
d(1) +d(2) +L+d(1997)
是否为偶数?
解 对于n的每个约数d,都有n = d×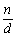 ,因此,n的正约数d与
,因此,n的正约数d与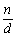 是成对地出现的。只有当d =
是成对地出现的。只有当d =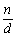 ,即n = d2时,d和
,即n = d2时,d和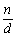 才是同一个数。故当且仅当n是完全平方数时,d(n)是奇数。
才是同一个数。故当且仅当n是完全平方数时,d(n)是奇数。
因为442 < 1997 < 452,所以在d(1), d(2), L, d(1997)中恰有44个奇数,故d(1) +d(2) +L+d(1997)是偶数。
例4 设凸2n边形M的顶点是A1, A2, L, A2n,点O在M的内部,用1, 2, L, 2n将M的2n条边分别编号,又将OA1, OA2, L, OA2n也同样进行编号,若把这些编号作为相应的线段的长度,证明:无论怎么编号,都不能使得三角形OA1A2, OA2A3, L, OA2nA1的周长都相等。
解 假设这些三角形的周长都相等,记为s。则
2ns = 3(1 + 2 +L+ 2n) = 3n(2n+ 1),
即
2s = 3(2n+ 1),
因此2½3(2n+ 1),这是不可能的,这个矛盾说明这些三角形的周长不可能全都相等。
例5 设整数k³ 1,证明:
(ⅰ) 若2k£n < 2k + 1,1 £a£n,a ¹ 2k,则2k a;
a;
(ⅱ) 若3k£ 2n- 1 < 3k + 1,1 £b£n,2b- 1¹ 3k,则3k 2b- 1。
2b- 1。
解 (ⅰ) 若2k|a,则存在整数q,使得a=q2k。显然q只可能是0或1。此时a= 0或2k,这都是不可能的,所以2k a;
a;
(ⅱ) 若 3k|2b-1,则存在整数q,使得2b-1=q3k,显然q只可能是0,1, 或2。此时2b-1= 0,3k,或 ,这都是不可能的,所以3k
,这都是不可能的,所以3k 2b- 1。
2b- 1。
例6 写出不超过100的所有的素数。
解 将不超过100的正整数排列如下:
1 2 3 4 5 6 7 8 9 10
11 12 13 14 15 16 17 18 19 20
21 22 23 24 25 26 27 28 29 30
31 32 33 34 35 36 37 38 39 40
41 42 43 44 45 46 47 48 49 50
51 52 53 54 55 56 57 58 59 60
61 62 63 64 65 66 67 68 69 70
71 72 73 74 75 76 77 78 79 80
81 82 83 84 85 86 87 88 89 90
91 92 93 94 95 96 97 98 99 100
按以下步骤进行:
(ⅰ) 删去1,剩下的后面的第一个数是2,2是素数;
(ⅱ) 删去2后面的被2整除的数,剩下的2后面的第一个数是3,3是素数;
(ⅲ) 再删去3后面的被3整除的数,剩下的3后面的第一个数是5,5是素数;
(ⅳ) 再删去5后面的被5整除的数,剩下的5后面的第一个数是7,7是素数;
LL
照以上步骤可以依次得到素数2, 3, 5, 7, 11, L。
由定理2推论可知,不超过100的合数必有一个不超过10的素约数,因此在删去7后面被7整除的数以后,就得到了不超过100的全部素数。
在例6中所使用的寻找素数的方法,称为Eratosthenes筛法。它可以用来求出不超过任何固定整数的所有素数。在理论上这是可行的;但在实际应用中,这种列出素数的方法需要大量的计算时间,是不可取的。
例7 证明:存在无穷多个正整数a,使得
n4+a(n = 1, 2, 3, L)
都是合数。
解 取a = 4k4,对于任意的nÎN,有
n4+ 4k4 = (n2+ 2k2)2- 4n2k2 = (n2+ 2k2+ 2nk)(n2+ 2k2- 2nk)。
因为
n2+ 2k2- 2nk = (n-k)2+k2³k2,
所以,对于任意的k = 2, 3, L以及任意的nÎN,n4+a是合数。
例8 设a1, a2, L, an是整数,且
a1+a2+L+an = 0,a1a2Lan = n,
则4½n。
解 如果2 n,则n, a1, a2, L, an都是奇数。于是a1+a2+L+an是奇数个奇数之和,不可能等于零,这与题设矛盾,所以2½n,即在a1, a2, L, an中至少有一个偶数。如果只有一个偶数,不妨设为a1,那么2
n,则n, a1, a2, L, an都是奇数。于是a1+a2+L+an是奇数个奇数之和,不可能等于零,这与题设矛盾,所以2½n,即在a1, a2, L, an中至少有一个偶数。如果只有一个偶数,不妨设为a1,那么2 ai(2 £i£n)。此时有等式
ai(2 £i£n)。此时有等式
a2+L+an = -a1,
在上式中,左端是(n- 1)个奇数之和,右端是偶数,这是不可能的,因此,在a1, a2, L, an中至少有两个偶数,即4½n。
例9 若n是奇数,则8½n2- 1。
解 设n = 2k+ 1,则
n2- 1= (2k+ 1)2- 1 = 4k(k+ 1)。
在k和k+ 1中有一个是偶数,所以8½n2- 1。
例9的结论虽然简单,却是很有用的。例如,使用例3中的记号,我们可以提出下面的问题:
问题 d(1)2+d(2)2+L+d(1997)2被4除的余数是多少?
例10 证明:方程
a12+a22 + a32 = 1999 (1)
无整数解。
解 若a1,a2,a3都是奇数,则存在整数A1,A2,A3,使得
a12 = 8A1+ 1,a22 = 8A2+ 1,a32 = 8A3+ 1,
于是
a12+a22 + a32 = 8(A1 + A2 + A3) + 3。
由于1999被8除的余数是7,所以a1,a2,a3不可能都是奇数。
由式(1),a1,a2,a3中只能有一个奇数,设a1为奇数,a2,a3为偶数,则存在整数A1,A2,A3,使得
a12 = 8A1+ 1,a22 = 8A2+r,a32 = 8A3+s,
于是
a12+a22 + a32 = 8(A1 + A2 + A3) + 1 +r+s,
其中r和s是整数,而且只能取值0或4。这样a12+a22+a32被8除的余数只可能是1或5,但1999被8除的余数是7,所以这样的a1,a2,a3也不能使式(2)成立。
综上证得所需要的结论。
习 题 一
1. 证明定理1。
2. 证明:若m-p½mn+pq,则m-p½mq+np。
3. 证明:任意给定的连续39个自然数,其中至少存在一个自然数,使得这个自然数的数字和能被11整除。
4. 设p是n的最小素约数,n = pn1,n1 > 1,证明:若p > ,则n1是素数。
,则n1是素数。
5. 证明:存在无穷多个自然数n,使得n不能表示为
a2+p(a > 0是整数,p为素数)
的形式。
第二节 带余数除法
在本节中,我们要介绍带余数除法及其简单应用。
定理1(带余数除法) 设a与b是两个整数,b¹ 0,则存在唯一的两个整数q和r,使得
a = bq+r,0 £r < |b|。 (1)
证明 存在性 若b½a,a = bq,qÎZ,可取r = 0。若b a,考虑集合
a,考虑集合
A = { a +kb;kÎZ },
其中Z表示所有整数的集合,以后,仍使用此记号,并以N表示所有正整数的集合。
在集合A中有无限多个正整数,设最小的正整数是r = a +k0b,则必有
0 < r < |b|, (2)
否则就有r ³ |b|。因为b a,所以r¹ |b|。于是r > |b|,即a +k0b > |b|,a +k0b- |b| > 0,这样,在集合A中,又有正整数a +k0b- |b| < r,这与r的最小性矛盾。所以式(2)必定成立。取q = - k0知式(1)成立。存在性得证。
a,所以r¹ |b|。于是r > |b|,即a +k0b > |b|,a +k0b- |b| > 0,这样,在集合A中,又有正整数a +k0b- |b| < r,这与r的最小性矛盾。所以式(2)必定成立。取q = - k0知式(1)成立。存在性得证。
唯一性 假设有两对整数q¢,r¢与q¢¢,r¢¢都使得式(1)成立,即
a = q¢¢b +r¢¢ = q¢b +r¢,0 £r¢, r¢¢ < |b|,
则
(q¢¢- q¢)b = r¢-r¢¢,|r¢- r¢¢| < |b|, (3)
因此r¢- r¢¢ = 0,r¢ = r¢¢,再由式(3)得出q¢ = q¢¢,唯一性得证。证毕。
定义1 称式(1)中的q是a被b除的商,r是a被b除的余数。
由定理1可知,对于给定的整数b,可以按照被b除的余数将所有的整数分成b类。在同一类中的数被b除的余数相同。这就使得许多关于全体整数的问题可以归化为对有限个整数类的研究。
以后在本书中,除特别声明外,在谈到带余数除法时总是假定b是正整数。
例1 设a,b,x,y是整数,k和m是正整数,并且
a = a1m+r1,0 £r1 < m,
b = b1m+r2,0 £r2 < m,
则ax +by和ab被m除的余数分别与r1x +r2y和r1r2被m除的余数相同。特别地,ak与r1k被m除的余数相同。
解 由
ax +by = (a1m+r1)x+ (b1m+r2)y = (a1x +b1y)m +r1x +r2y
可知,若r1x +r2y被m除的余数是r,即
r1x +r2y = qm +r,0 £r < m,
则
ax +by = (a1x +b1y +q)m +r,0 £r < m,
即ax +by被m除的余数也是r。
同样方法可以证明其余结论。
例2 设a1, a2, L, an为不全为零的整数,以y0表示集合
A = { y;y = a1x1+L+ anxn,xiÎZ,1 £i£n }
中的最小正数,则对于任何yÎA,y0½y;特别地,y0½ai,1 £i£n。
解 设y0 = a1x1¢+L+ anxn¢,对任意的y = a1x1+L+ anxnÎA,由定理1,存在q, r0ÎZ,使得
y = qy0+r0,0 £r0 < y0 。
因此
r0 = y-qy0 = a1(x1-qx1¢)+L+ an(xn-qxn¢)ÎA。
如果r0¹ 0,那么,因为0 < r0 < y0,所以r0是A中比y0还小的正数,这与y0的定义矛盾。所以r0 = 0,即y0½y。
显然aiÎA(1 £i£n),所以y0整除每个ai(1 £i£n)。
例3 任意给出的五个整数中,必有三个数之和被3整除。
解 设这五个数是ai,i = 1, 2, 3, 4, 5,记
ai = 3qi+ri,0 £ ri < 3,i = 1, 2, 3, 4, 5。
分别考虑以下两种情形:
(ⅰ) 若在r1, r2, L, r5中数0,1,2都出现,不妨设r1 = 0,r2 = 1,r3 = 2,此时
a1+a2+ a3 = 3(q1+q2+q3)+ 3
可以被3整除;
(ⅱ) 若在r1, r2, L, r5中数0,1,2至少有一个不出现,这样至少有三个ri要取相同的值,不妨设r1 = r2 = r3 = r(r = 0,1或2),此时
a1+a2+ a3 = 3(q1+q2+q3)+ 3r
可以被3整除。
例4 设a0, a1, L, anÎZ,f(x) = anxn+L+a1x +a0 ,已知f(0)与f(1)都不是3的倍数,证明:若方程f(x) = 0有整数解,则
3½f(-1) = a0-a1+ a2-L+ (-1)nan。
解 对任何整数x,都有
x = 3q +r,r = 0,1或2,qÎZ。
(ⅰ) 若r = 0,即x = 3q,qÎZ,则
f(x) = f(3q) = an(3q)n+L+a1(3q)+a0 = 3Q1+ a0 = 3Q1+ f(0),
其中Q1ÎZ,由于f(0)不是3的倍数,所以f(x) ¹ 0;
(ⅱ) 若r = 1,即x = 3q + 1,qÎZ,则
f(x) = f(3q + 1) = an(3q + 1)n+L+a1(3q + 1)+a0
= 3Q2+an+L+a1+ a0 = 3Q2+ f(1),
其中Q2ÎZ。由于f(1)不是3的倍数,所以f(x) ¹ 0。
因此若f(x) = 0有整数解x,则必是x = 3q + 2 = 3q¢- 1,q¢ÎZ,于是
0 = f(x) = f(3q¢- 1) = an(3q¢- 1)n+L+a1(3q¢- 1)+a0
= 3Q3+ a0-a1+ a2-L+ (- 1)nan = 3Q3+ f(-1),
其中Q3ÎZ。所以3½f(-1) = a0-a1+a2-L+ (-1)nan 。
例5 证明:对于任意的整数n,f(n) = 3n5+ 5n3+ 7n被15整除。
解 对于任意的正整数n,记
n = 15q +r,0 £r < 15。
由例1,
n2 = 15Q1+r1,n4 = 15Q2+r2,
其中r1与r2分别是r2与r4被15除的余数。
以R表示3n4+ 5n2+ 7被15除的余数,则R就是3r2+ 5r1+ 7被15除的余数,而且f(n)被15除的余数就是rR被15除的余数,记为R¢。
当r = 0时,显然R¢ = 0,即15½3n5+ 5n3+ 7n。
对于r = 1, 2, 3, L, 14的情形,通过计算列出下表:
r = 1, 14 2, 13 3, 12 4, 11 5, 10 6, 9 7, 8
r1 = 1 4 9 1 10 6 4
r2 = 1 1 6 1 10 6 1
R = 0 0 10 0 12 10 0
R¢= 0 0 0 0 0 0 0
这证明了结论。
例6 设n是奇数,则16½n4+ 4n2+ 11。
解 我们有
n4+ 4n2+ 11 = (n2- 1)(n2+ 5)+ 16。
由第一节例题9,有8½n2- 1,由此及2½n2+ 5得到16½(n2- 1)(n2+ 5)。
例7 证明:若a被9除的余数是3,4,5或6,则方程x3+y3 = a没有整数解。
解 对任意的整数x,y,记
x = 3q1+r1,y = 3q2+r2,0 £r1, r2 < 3。
则存在Q1, R1, Q2, R2ÎZ,使得
x3 = 9Q1+R1,y3 = 9Q2+R2 ,
其中R1和R2被9除的余数分别与r13和r23被9除的余数相同,即
R1 = 0,1或8,R2 = 0,1或8。 (4)
因此
x3+y3 = 9(Q1+Q2)+R1+R2 。
又由式(4)可知,R1+R2被9除的余数只可能是0,1,2,7或8,所以,x3+y3不可能等于a。
习 题 二
1. 证明:12½n4+ 2n3+ 11n2+ 10n,nÎZ。
2. 设3½a2+b2,证明:3½a且3½b。
3. 设n,k是正整数,证明:nk与nk + 4的个位数字相同。
4. 证明:对于任何整数n,m,等式n2+ (n + 1)2 = m2+ 2不可能成立。
5. 设a是自然数,问a4- 3a2+ 9是素数还是合数?
6. 证明:对于任意给定的n个整数,必可以从中找出若干个作和,使得这个和能被n整除。
第三节 最大公约数
定义1 整数a1, a2, L, ak的公共约数称为a1, a2, L, ak的公约数。不全为零的整数a1, a2, L, ak的公约数中最大的一个叫做a1, a2, L, ak的最大公约数(或最大公因数),记为(a1, a2, L, ak)。
由于每个非零整数的约数的个数是有限的,所以最大公约数是存在的,并且是正整数。
如果(a1, a2, L, ak)=1,则称a1, a2, L, ak是互素的(或互质的);如果
(ai, a j)=1,1 £i, j £k,i¹ j,
则称a1, a2, L, ak是两两互素的(或两两互质的)。
显然,a1, a2, L, ak两两互素可以推出(a1, a2, L, ak) =1,反之则不然,例如(2, 6, 15)=1,但(2, 6) = 2。
定理1 下面的等式成立:
(ⅰ) (a1, a2, L, ak)=(|a1|, |a2|, L, |ak|);
(ⅱ) (a, 1)=1,(a, 0)=|a|,(a, a)=|a|;
(ⅲ) (a, b)=(b, a);
(ⅳ) 若p是素数,a是整数,则(p, a)=1或p½a;
(ⅴ) 若a = bq + r,则(a, b)=(b, r)。
证明 (ⅰ)--(ⅳ)留作习题。
(ⅴ) 由第一节定理1可知,如果d½a,d½b,则有d½r = a -bq,反之,若d½b,d½r,则d½a = bq + r。因此a与b的全体公约数的集合就是b与r的全体公约数的集合,这两个集合中的最大正数当然相等,即(a, b)=(b, r)。证毕。
由定理1可知,在讨论(a1, a2, L, an)时,不妨假设a1, a2, L, an是正整数,以后我们就维持这一假设。
定理2 设a1, a2, L, akÎZ,记
A ={ y;y = ,xiÎZ,1£i£k }。
,xiÎZ,1£i£k }。
如果y0是集合A中最小的正数,则y0=(a1, a2, L, ak)。
证明 设d是a1, a2, L, ak的一个公约数,则d½y0,所以d£y0。另一方面,由第二节例2知,y0也是a1, a2, L, ak的公约数。因此y0是a1, a2, L, ak的公约数中的最大者,即y0=( a1, a2, L, ak)。证毕。
推论1 设d是a1, a2, L, ak的一个公约数,则d½(a1, a2, L, ak)。
这个推论对最大公约数的性质做了更深的刻划:最大公约数不但是公约数中的最大的,而且是所有公约数的倍数。
推论2 (ma1, ma2, L, mak)=|m|(a1, a2, L, ak)。
推论3 记d=(a1, a2, L, ak),则
 = 1,
= 1,
特别地,  = 1。
= 1。
定理3 (a1, a2, L, ak)=1的充要条件是存在整数x1, x2, L, xk,使得
a1x1+ a2x2+L+ akxk=1。 (1)
证明 必要性 由定理2得到。
充分性 若式(1)成立,如果 (a1, a2, L, ak)= d > 1,那么由d½ai(1 £i £k)推出d½a1x1+a2x2+L+akxk=1,这是不可能的。所以有(a1, a2, L, ak)= 1。证毕。
定理4 对于任意的整数a,b,c,下面的结论成立:
(ⅰ) 由b½ac及(a, b)=1可以推出b½c;
(ⅱ) 由b½c,a½c及(a, b)=1可以推出ab½c。
证明 (ⅰ) 若(a, b)=1,由定理2,存在整数x与y,使得
ax + by =1。
因此
acx + bcy = c。 (2)
由上式及b½ac得到b½c。结论(ⅰ)得证;
(ⅱ) 若(a, b)=1,则存在整数x,y使得式(2)成立。由b½c与a½c得到ab½ac,ab½bc,再由式(2)得到ab½c。结论(ⅱ)得证。证毕。
推论1 若p是素数,则下述结论成立:
(ⅰ) p½abÞp½a或p½b;
(ⅱ) p½a2Þp½a。
证明 留作习题。
推论2 若 (a, b)=1,则(a, bc)=(a, c)。
证明 设d是a与bc的一个公约数,则d½a,d½bc,由式(2)得到,d|c, 即d是a与c的公约数。另一方面,若d是a与c的公约数,则它也是a与bc的公约数。因此,a与c的公约数的集合,就是a与bc的公约数的集合,所以(a, bc)=(a, c)。证毕。
推论3 若 (a, bi)=1,1 £i£n,则(a, b1b2Lbn)=1。
证明 留作习题。
定理5 对于任意的n个整数a1, a2, L, an,记
(a1, a2)= d2,(d2, a3)= d3,L,(dn - 2, an - 1)= dn - 1,(dn - 1, an)= dn,
则
dn=(a1, a2, L, an)。
证明 由定理2的推论,我们有
dn=(dn - 1, an) Þdn½an,dn½dn - 1,
dn - 1=(dn - 2, an - 1) Þdn - 1½an - 1,dn - 1½dn - 2,
Þdn½an,dn½an - 1,dn½dn - 2,
dn - 2=(dn - 3, an - 2) Þdn - 2½an - 2,dn - 2½dn - 3
Þdn½an,dn½an - 1,dn½an - 2,dn½dn - 3,
LL
d2=(a1, a2) Þ dn½an,dn½an - 1,L,dn½a2,dn½a1,
即dn是a1, a2, L, an的一个公约数。
另一方面,对于a1, a2, L, an的任何公约数d,由定理2的推论及d2, L, dn的定义,依次得出
d½a1,d½a2Þd½d2,
d½d2,d½a3Þd½d3,
LL
d½dn - 1,d½anÞd½dn,
因此dn是a1, a2, L, an的公约数中的最大者,即dn=(a1, a2, L, an)。证毕。
例1 证明:若n是正整数,则 是既约分数。
是既约分数。
解 由定理1得到
(21n+4, 14n +3)=(7n +1, 14n +3)=(7n +1, 1)=1。
注:一般地,若(x, y) = 1,那么,对于任意的整数a,b,有
(x, y) = (x-ay, y) = (x-ay, y-b(x-ay)) = (x-ay, (ab+ 1)y-bx),
因此,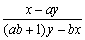 是既约分数。
是既约分数。
例2 证明:121 n2+2n +12,nÎZ。
n2+2n +12,nÎZ。
解 由于121=112,n2+2n +12=(n +1)2+11,所以,若
112½(n +1)2+11, (3)
则11½(n +1)2,因此,由定理4的推论1得到
11½n +1,112½(n +1)2。
再由式(3)得到
112½11,
这是不可能的。所以式(3)不能成立。
注:这个例题的一般形式是:
设p是素数,a,b是整数,则
pk (an + b)k+ pk - 1c,
(an + b)k+ pk - 1c,
其中c是不被p整除的任意整数,k是任意的大于1的整数。
例3 设a,b是整数,且
9½a2+ ab + b2, (4)
则3½(a, b)。
解 由式(4)得到
9½(a -b)2+3abÞ 3½(a -b)2+3ab
Þ 3½(a -b)2Þ3½a -b (5)
Þ 9½(a -b)2。
再由式(4)得到
9½3abÞ 3½ab。
因此,由定理4的推论1,得到
3½a或3½b。
若3½a,由式(5)得到3½b;若3½b,由(5)式也得到3½a。因此,总有3½a且3½b。
由定理2的推论推出3½(a, b)。
例4 设a和b是正整数,b > 2,则2b- 1 2a+1。
2a+1。
解 (ⅰ) 若a < b,且
2b- 1½2a+1。 (6)
成立,则
2b- 1 £ 2a+1 Þ 2b- 2a£ 2 Þ 2a(2b -a- 1) £ 2,
于是a = 1,b -a = 1,即b = 2,这是不可能的,所以式(6)不成立。
(ⅱ) 若a = b,且式(6)成立,则由式(6)得到
2a- 1½(2a- 1)+2 Þ 2a- 1½2 Þ 2a- 1 £ 2 Þ 2a£ 3,
于是b = a = 1,这是不可能的,所以式(6)不成立。
(ⅲ) 若a > b,记a = kb + r,0 £r < b,此时
2kb- 1=(2b- 1)(2(k - 1)b+2(k - 2)b+L+1)=(2b- 1)Q,
其中Q是整数。所以
2a+1=2kb + r+1=2r(2kb- 1+1)+1
=2r((2b- 1)Q +1)+1 = (2b- 1)Q¢+(2r+1),
其中Q¢是整数。因此
2b- 1½2a+1 Þ 2b- 1½2r+1,
在(ⅰ)中已经证明这是不可能的,所以式(6)不能成立。
综上证得2b- 1 2a+1。
2a+1。
习 题 三
1. 证明定理1中的结论(ⅰ)—(ⅳ)。
2. 证明定理2的推论1, 推论2和推论3。
3. 证明定理4的推论1和推论3。
4. 设x,yÎZ,17½2x +3y,证明:17½9x +5y。
5. 设a,b,cÎN,c无平方因子,a2½b2c,证明:a½b。
6. 设n是正整数,求 的最大公约数。
的最大公约数。
第四节 最小公倍数
定义1 整数a1, a2, L, ak的公共倍数称为a1, a2, L, ak的公倍数。a1, a2, L, ak的正公倍数中的最小的一个叫做a1, a2, L, ak的最小公倍数,记为[a1, a2, L, ak]。
定理1 下面的等式成立:
(ⅰ) [a, 1] = |a|,[a, a] = |a|;
(ⅱ) [a, b] = [b, a];
(ⅲ) [a1, a2, L, ak] = [|a1|,|a2| L, |ak|];
(ⅳ) 若a½b,则[a, b] = |b|。
证明 留作习题。
由定理1中的结论(ⅲ)可知,在讨论a1, a2, L, ak的最小公倍数时,不妨假定它们都是正整数。在本节中总是维持这一假定。
最小公倍数和最大公约数之间有一个很重要的关系,即下面的定理。
定理2 对任意的正整数a,b,有
[a, b] = 。
。
证明 设m是a和b的一个公倍数,那么存在整数k1,k2,使得m = ak1,m = bk2,因此
ak1 = bk2 。 (1)
于是
 。
。
由于 = 1,所以由第三节定理4得到
= 1,所以由第三节定理4得到
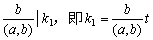 ,
,
其中t是某个整数。将上式代入式(1)得到
m = t。 (2)
t。 (2)
另一方面,对于任意的整数t,由式(2)所确定的m显然是a与b的公倍数,因此a与b的公倍数必是式(2)中的形式,其中t是整数。当t = 1时,得到最小公倍数
[a, b] = 。
。
证毕。
推论1 两个整数的任何公倍数可以被它们的最小公倍数整除。
证明 由式(2)可得证。证毕。
这个推论说明:两个整数的最小公倍数不但是最小的正倍数,而且是另外的公倍数的约数。
推论2 设m,a,b是正整数,则[ma, mb] = m[a, b]。
证明 由定理2及第三节定理2的推论得到
[ma, mb] = = m[a, b]。
= m[a, b]。
证毕。
定理3 对于任意的n个整数a1, a2, L, an,记
[a1, a2] = m2,[m2, a3] = m3,L,[mn-2, an-1] = mn-1,[mn-1, an] = mn,
则
[a1, a2, L, an] = mn。
证明 我们有
mn = [mn-1, an] Þmn-1½mn,an½mn,
mn-1 = [mn-2, an-1] Þmn-2½mn-1½mn,an½mn,an-1½mn-1½mn,
mn-2 = [mn-3, an-2] Þmn-3½mn-2½mn,an½mn,an-1½mn,an-2½mn,
LL
m2 = [a1, a2] Þan½mn,L,a2½mn,a1½mn,
即mn是a1, a2, L, an的一个公倍数。
另一方面,对于a1, a2, L, an的任何公倍数m,由定理2的推论及m2, L, mn的定义,得
m2½m,m3½m,L,mn½m。
即mn是a1, a2, L, an最小的正的公倍数。证毕。
推论 若m是整数a1, a2, L, an的公倍数,则[a1, a2, L, an]½m。
证明 留作习题。
定理4 整数a1, a2, L, an两两互素,即
(ai, aj) = 1,1 £i, j £n,i ¹j
的充要条件是
[a1, a2, L, an] = a1a2Lan 。 (3)
证明 必要性 因为(a1, a2) = 1,由定理2得到
[a1, a2] = = a1a2 。
= a1a2 。
由(a1, a3) = (a2, a3) = 1及第三节定理4推论3得到
(a1a2, a3) = 1,
由此及定理3得到
[a1, a2, a3] = [[a1, a2], a3] = [a1a2, a3] = a1a2a3 。
如此继续下去,就得到式(3)。
充分性 用归纳法证明。当n = 2时,式(3)成为[a1, a2] = a1a2。由定理2
a1a2 = [a1, a2] = Þ (a1, a2) = 1,
Þ (a1, a2) = 1,
即当n = 2时,充分性成立。
假设充分性当n = k时成立,即
[a1, a2, L, ak] = a1a2LakÞ (ai, aj) = 1,1 £i, j £k,i ¹j。
对于整数a1, a2, L, ak, ak + 1,使用定理3中的记号,由定理3可知
[a1, a2, L, ak, ak + 1] = [mk, ak + 1]。 (4)
其中mk = [a1, a2, L, ak]。因此,如果
[a1, a2, L, ak, ak + 1] = a1a2Lakak + 1,
那么,由此及式(4)得到
[a1, a2, L, ak, ak + 1] = [mk, ak + 1] =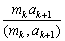 = a1a2Lakak + 1,
= a1a2Lakak + 1,
即
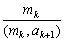 = a1a2Lak,
= a1a2Lak,
显然mk£ a1a2Lak,(mk, ak + 1) ³ 1。所以若使上式成立,必是
(mk, ak + 1) = 1, (5)
并且
mk = a1a2Lak 。 (6)
由式(6)与式(5)推出
(ai, ak + 1) = 1,1 £i£k; (7)
由式(6)及归纳假设推出
(ai, aj) = 1,1 £i, j £k,i ¹j。 (8)
综合式(7)与式(8),可知当n = k+ 1时,充分性成立。由归纳法证明了充分性。证毕。
定理4有许多应用。例如,如果m1, m2, L, mk是两两互素的整数,那么,要证明m = m1m2Lmk整除某个整数Q,只需证明对于每个i,1 £i£k,都有mi½Q。这一点在实际计算中是很有用的。对于函数f(x),要验证命题“m½f(n),nÎZ”是否成立,可以用第二节例5中的方法,验证“m½f(r),r = 0, 1, L, m- 1”是否成立。这需要做m次除法。但是,若分别验证“mi½f(ri),ri = 0, 1, L, mi- 1,1 £i£k”是否成立,则总共需要做m1+m2+L+mk次除法。后者的运算次数显然少于前者。
例1 设a,b,c是正整数,证明:[a, b, c](ab, bc, ca) = abc。
解 由定理3和定理2有
[a, b, c] = [[a, b], c] = , (9)
, (9)
由第三节定理5和定理2的推论,
(ab, bc, ca) = (ab, (bc, ca)) = (ab, c(a, b))
= 。 (10)
。 (10)
联合式(9)与式(10)得到所需结论。
例2 对于任意的整数a1, a2, L, an及整数k,1 £k £n,证明:
[a1, a2, L, an] = [[a1,L, ak],[ak + 1, L, an]]
解 因为[a1, a2, L, an]是a1, L, ak, ak + 1, L, an的公倍数,所以由定理2推论,推出
[a1, L, ak]½[a1, a2, L, an],
[ak + 1, L, an]½[a1, a2, L, an],
再由定理3推论知
[[a1, L, ak], [ak + 1, L, an]]½[a1, a2, L, an]。 (11)
另一方面,对于任意的ai(1 £i£n),显然
ai½[[a1, L, ak], [ak + 1, L, an]],
所以由定理3推论可知
[a1, a2, L, an]½[[a1, L, ak], [ak + 1, L, an]],
联合上式与式(11)得证。
例3 设a,b,c是正整数,证明:
[a, b, c][ab, bc, ca] = [a, b][b, c][c, a]。
解 由定理2推论2及例2,有
[a, b, c][ab, bc, ca] = [[a, b, c]ab, [a, b, c]bc, [a, b, c]ca]
= [[a2b, ab2, abc], [abc, b2c, bc2], [a2c, abc, ac2]]
= [a2b, ab2, abc, abc, b2c, bc2, a2c, abc, ac2]
= [abc, a2b, a2c, b2c, b2a, c2a, c2b]
以及
[a, b][b, c][c, a] = [[a, b]b, [a, b]c][c, a]
= [ab, b2, ac, bc][c, a]
= [ab[c, a], b2[c, a], ac[c, a], bc[c, a]]
= [abc, a2b, b2c, b2a, ac2, a2c, bc2, bca]
= [abc, a2b, a2c, b2c, b2a, c2a, c2b],
由此得证。
习 题 四
1. 证明定理1。
2. 证明定理3的推论。
3. 设a,b是正整数,证明:(a+b)[a, b] = a[b, a+b]。
4. 求正整数a,b,使得a+b = 120,(a, b) = 24,[a, b] = 144。
5. 设a,b,c是正整数,证明:
 。
。
6. 设k是正奇数,证明:1 + 2 +L+ 9½1k+ 2k+L+ 9k。
第五节 辗转相除法
本节要介绍一个计算最大公约数的算法——辗转相除法,又称Euclid算法。它是数论中的一个重要方法,在其他数学分支中也有广泛的应用。
定义1 下面的一组带余数除法,称为辗转相除法。
设a和b是整数,b ¹ 0,依次做带余数除法:
a = bq1+r1, 0 < r1 < |b|,
b = r1q2+r2, 0 < r2 < r1 ,
LL
rk - 1 = rkqk + 1+rk + 1,0 < rk + 1 < rk, (1)
LL
rn - 2 = rn - 1qn+rn, 0 < rn < rn-1 ,
rn - 1 = rnqn + 1 。
由于b是固定的,而且
|b| > r1 > r2 > L,
所以式(1)中只包含有限个等式。
下面,我们要对式(1)所包含的等式的个数,即要做的带余数除法的次数进行估计。
引理1 用下面的方式定义Fibonacci数列{Fn}:
F1 = F2 = 1,Fn = Fn - 1+Fn- 2,n ³3,
那么对于任意的整数n ³ 3,有
Fn > an - 2, (2)
其中a= 。
。
证明 容易验证
a2 = a+ 1。
当n = 3时,由
F3 = 2 > = a
= a
可知式(2)成立。
假设式(2)对于所有的整数k £n(n ³ 3)成立,即
Fk> ak - 2,k £n,
则
Fn + 1 = Fn+Fn - 1 > a n - 2+a n - 3 = a n - 3(a+ 1) = a n - 3a2 = a n- 1,
即当k = n+ 1时式(2)也成立。由归纳法知式(2)对一切n ³ 3成立。证毕。
定理1(Lame) 设a, bÎN,a > b,使用在式(1)中的记号,则
n < 5log10b。
证明 在式(1)中,rn³ 1,qn + 1³ 2,qi³ 1(1 £i £n),因此
rn³ 1 = F2 ,
rn - 1³ 2rn³ 2 = F3 ,
rn - 2³rn - 1+rn³F3 + F2 = F4 ,
LL
b ³r1+r2³Fn + 1+Fn = Fn + 2 ,
由此及式(2)得
b³an = ,
,
即
log10b³nlog10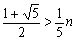 ,
,
这就是定理结论。证毕。
定理2 使用式(1)中的记号,记
P0 = 1,P1 = q1,Pk = qkPk - 1+Pk - 2,k ³ 2,
Q0 = 0,Q1 = 1,Qk = qkQk - 1+Qk - 2,k ³ 2,
则
aQk-bPk = (-1)k - 1rk,k = 1, 2, L, n 。 (3)
证明 当k = 1时,式(3)成立。
当k = 2时,有
Q2 = q2Q1+Q0 = q2,P2 = q2P1+P0 = q2q1+ 1,
此时由式(1)得到
aQ2-bP2 = aq2-b(q2q1+ 1) = (a -bq1)q2-b = r1q2-b =-r2,
即式(3)成立。
假设对于k < m(1 £m £n)式(3)成立,由此假设及式(1)得到
aQm-bPm= a(qmQm - 1+Qm - 2)-b(qmPm - 1+Pm - 2)
= (aQm - 1-bPm - 1)qm+ (aQm - 2-bPm - 2)
= (-1)m - 2rm - 1qm+ (-1)m - 3rm - 2
= (-1)m - 1(rm - 2-rm - 1qm) = (-1)m- 1rm,
即式(3)当k = m时也成立。定理由归纳法得证。证毕。
定理3 使用式(1)中的记号,有rn = (a, b)。
证明 由第三节定理1,从式(1)可见
rn = (rn - 1, rn) = (rn - 2, rn - 1) = L = (r1, r2) = (b, r1) = (a, b)。
证毕。
现在我们已经知道,利用辗转相除法可以求出整数x,y,使得
ax+by = (a, b)。 (4)
为此所需要的除法次数是O(log10b)。但是如果只需要计算(a, b)而不需要求出使式(4)成立的整数x与y,则所需要的除法次数还可更少一些。
例1 设a和b是正整数,那么只使用被2除的除法运算和减法运算就可以计算出(a, b)。
解 下面的四个基本事实给出了证明:
(ⅰ) 若a½b,则(a, b) = a;
(ⅱ) 若a = 2aa1, ,a³b³ 1,则
,a³b³ 1,则
(a, b) = 2b(2a-ba1, b1);
(ⅲ) 若 ,则(a, b) = (a, b1);
,则(a, b) = (a, b1);
(ⅳ) 若 。
。
在实际计算过程中,若再灵活运用最大公约数的性质(例如第三节定理4的推论),则可使得求最大公约数的过程更为简单。
例2 用辗转相除法求(125, 17),以及x,y,使得
125x+ 17y = (125, 17)。
解 做辗转相除法:
125 = 7×17 + 6,q1 = 7,r1 = 6,
17 = 2×6 + 5,q2 = 2,r2 = 5,
6 = 1×5 + 1,q3 = 1,r3 = 1,
5 = 5×1, q4 = 5。
由定理4,(125, 17) = r3 = 1。
利用定理2计算(n = 3)
P0 = 1,P1 = 7,P2 = 2×7 + 1 = 15,P3 = 1×15 + 7 = 22,
Q0 = 0,Q1 = 1,Q2 = 2×1 + 0 = 2,Q3 = 1×2 + 1 = 3,
取x = (-1)3 - 1Q3 = 3,y = (-1)3P3 = -22,则
125×3 + 17×(-22) = (125, 17) = 1。
例3 求(12345, 678)。
解 (12345, 678) = (12345, 339) = (12006, 339) = (6003, 339)
= (5664, 339) = (177, 339) = (177, 162) = (177, 81)
= (96, 81) = (3, 81) = 3。
例4 在m个盒子中放若干个硬币,然后以下述方式往这些盒子里继续放硬币:每一次在n(n < m)个盒子中各放一个硬币。证明:若(m, n) = 1,那么无论开始时每个盒子中有多少硬币,经过若干次放硬币后,总可使所有盒子含有同样数量的硬币。
解 由于(m, n) = 1,所以存在整数x,y,使得mx+ny = 1。因此对于任意的自然数k,有
1 +m(-x+kn) = n(km+y),
这样,当k充分大时,总可找出正整数x0,y0,使得
1 +mx0 = ny0 。
上式说明,如果放y0次(每次放n个),那么在使m个盒子中各放x0个后,还多出一个硬币。把这个硬币放入含硬币最少的盒子中(这是可以做到的),就使它与含有最多硬币的盒子所含硬币数量之差减少1。因此经过若干次放硬币后,必可使所有盒子中的硬币数目相同。
习 题 五
1. 说明例1证明中所用到的四个事实的依据。
2. 用辗转相除法求整数x,y,使得1387x - 162y = (1387, 162)。
3. 计算:(27090, 21672, 11352)。
4. 使用引理1中的记号,证明:(Fn + 1, Fn) = 1。
5. 若四个整数2836,4582,5164,6522被同一个大于1的整数除所得的余数相同,且不等于零,求除数和余数各是多少?
6. 记Mn=2n- 1,证明:对于正整数a,b,有(Ma, Mb)= M(a, b)。
第六节 算术基本定理
在本节中,我们要介绍整数与素数的一个重要关系,即任何大于1的正整数都可以表示成素数的乘积。
引理1 任何大于1的正整数n可以写成素数之积,即
n = p1p2Lpm, (1)
其中pi(1 £i £m)是素数。
证明 当n = 2时,结论显然成立。
假设对于2 £n £k,式(1)成立,我们来证明式(1)对于n = k+ 1也成立,从而由归纳法推出式(1)对任何大于1的整数n成立。
如果k+ 1是素数,式(1)显然成立。
如果k+ 1是合数,则存在素数p与整数d,使得k+ 1 = pd。由于2 £d £k,由归纳假定知存在素数q1, q2, L, ql,使得d = q1q2Lql,从而k+ 1 = pq1q2Lql。证毕。
定理1(算术基本定理) 任何大于1的整数n可以唯一地表示成
n =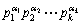 , (2)
, (2)
其中p1, p2, L, pk是素数,p1 < p2 < L < pk,a1, a2, L, ak是正整数。
证明 由引理1,任何大于1的整数n可以表示成式(2)的形式,因此,只需证明表示式(2)的唯一性。
假设pi(1 £i £k)与qj(1 £j £l)都是素数,
p1£p2£L£pk,q1£q2£L£ql, (3)
并且
n = p1p2Lpk = q1q2Lql , (4)
则由第三节定理4推论1,必有某个qj(1 £j£l),使得p1½qj,所以p1 = qj;又有某个pi(1 £i£k),使得q1½pi,所以q1 = pi。于是,由式(3)可知p1 = q1,从而由式(4)得到
p2Lpk = q2Lql 。
重复上述这一过程,得到
k = l,pi = qi,1 £i £k。
证毕。
定义1 使用定理1中的记号,称
n =
是n的标准分解式,其中pi(1 £i £k)是素数,p1 < p2 < L < pk,a i(1 £i £k)是正整数。
推论1 使用式(2)中的记号,有
(ⅰ) n的正因数d必有形式
d = ,giÎZ,0 £gi£a i,1 £i £k;
,giÎZ,0 £gi£a i,1 £i £k;
(ⅱ) n的正倍数m必有形式
m = M,MÎN,biÎN,bi³a i,1 £i £k。
M,MÎN,biÎN,bi³a i,1 £i £k。
证明 留作习题。
推论2 设正整数a与b的标准分解式是
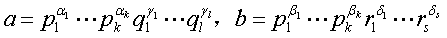
其中pi(1 £i £k),qi(1 £i £l)与ri(1 £i £s)是两两不相同的素数,ai,bi(1 £i £k),gi(1 £i £l)与di(1 £i £s)都是正整数,则
(a, b) = , li = min{ai, bi },1 £i £k,
, li = min{ai, bi },1 £i £k,
[a, b] = ,mi = max{ai, bi },1 £i £k。
,mi = max{ai, bi },1 £i £k。
证明 留作习题。
为了方便,推论2常叙述为下面的形式:
推论2¢ 设正整数a与b的标准分解式是
 ,
,
其中p1, p2, L, pk是互不相同的素数,ai,bi(1 £i £k)都是非负整数,则
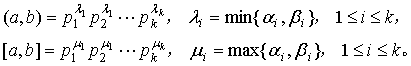
推论3 设a,b,c,n是正整数,
ab = cn,(a, b) = 1, (5)
则存在正整数u,v,使得
a = un,b = vn,c = uv,(u, v) = 1。
证明 设c = ,其中p1, p2, L, pk是互不相同的素数,gi(1 £i £k)是正整数。又设
,其中p1, p2, L, pk是互不相同的素数,gi(1 £i £k)是正整数。又设
 ,
,
其中aI,bi(1 £i £k)都是非负整数。由式(5)及推论2¢可知
min{ai, bi} = 0,ai+bi = ngi,1 £i £k,
因此,对于每个i(1 £i £k),等式
ai = ngi ,bi = 0与ai = 0,bi = ngi
有且只有一个成立。这就证明了推论。证毕。
例1 写出51480的标准分解式。
解 我们有
51480 = 2×25740 = 22×12870 = 23×6435
= 23×5×1287 = 23×5×3×429
= 23×5×32×143 = 23×32×5×11×13。
例2 设a,b,c是整数,证明:
(ⅰ) (a, b)[a, b] = ab;
(ⅱ) (a, [b, c]) = [(a, b), (a, c)]。
解 为了叙述方便,不妨假定a,b,c是正整数。
(ⅰ) 设
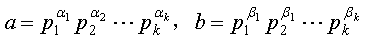 ,
,
其中p1, p2, L, pk是互不相同的素数,ai,bi(1 £i £k)都是非负整数。由定理1推论2¢,有
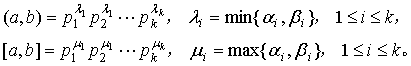
由此知
(a, b)[a, b] =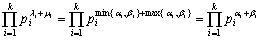 =ab;
=ab;
(ⅱ) 设
 ,
,
其中p1, p2, L, pk是互不相同的素数,ai,bi,gi(1 £i £k)都是非负整数。由定理1推论2¢,有
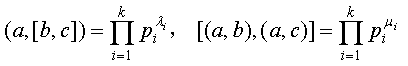 ,
,
其中,对于1 £i £k,有
li = min{ai, max{bi, gi}},
mi = max{min{ai, bi}, min{ai, gi}},
不妨设bi£gi,则
min{ai, bi} £ min{ai, gi},
所以
mi = min{ai, gi} = li,
即(a, [b, c]) = [(a, b), (a, c)]。
注:利用定理1可以容易地处理许多像例2这样的问题。
例3 证明: (n ³ 2)不是整数。
(n ³ 2)不是整数。
解 设
3k£ 2n - 1 < 3k + 1。
对于任意的1 £i £n,2i - 1 ¹ 3k,记
2i - 1 = Qi,QiÎZ,
Qi,QiÎZ,
由第一节例5,知ai£k - 1。因为3k - 1Q1Q2LQ2n - 1是整数,所以,如果N是整数,则存在整数Q,使得
3k - 1Q1Q2LQ2n - 1N = Q+ 3k- 1Q1Q2LQ2n -1 。
。
由于3 Q1Q2LQ2n-1,所以上式右端不是整数,这个矛盾说明N不能是整数。
Q1Q2LQ2n-1,所以上式右端不是整数,这个矛盾说明N不能是整数。
习 题 六
1. 证明定理1的推论1。
2. 证明定理1的推论2。
3. 写出22345680的标准分解式。
4. 证明:在1, 2, L, 2n中任取n+ 1数,其中至少有一个能被另一个整除。
5. 证明: (n ³ 2)不是整数。
(n ³ 2)不是整数。
6. 设a,b是正整数,证明:存在a1,a2,b1,b2,使得
a = a1a2,b = b1b2,(a2, b2) = 1,
并且[a, b] = a2b2。
第七节 函数[x]与{x}
本节中要介绍函数[x],它在许多数学问题中有广泛的应用。
定义1 设x是实数,以[x]表示不超过x的最大整数,称它为x的整数部分,又称{x} = x- [x]为x的小数部分。
定理1 设x与y是实数,则
(ⅰ) x£yÞ [x] £ [y];
(ⅱ) 若m是整数,则[m+x] = m+ [x];
(ⅲ) 若0 £x < 1,则[x] = 0;
(ⅳ) [x+y] = ;
;
(ⅴ) [-x] = ;
;
(ⅵ) {-x} = 。
。
证明 留作习题。
定理2 设a与b是正整数,则在1, 2, L, a中能被b整除的整数有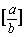 个。
个。
证明 能被b整除的正整数是b, 2b, 3b, L,因此,若数1, 2, L, a中能被b整除的整数有k个,则
kb £a < (k+ 1)bÞk £ < k+ 1 Þk =
< k+ 1 Þk =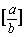 。
。
证毕。
由定理2我们看到,若b是正整数,那么对于任意的整数a,有
 ,
,
即在带余数除法
a = bq+r,0 £r < b
中有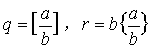 。
。
定理3 设n是正整数,n! = 是n!的标准分解式,则
是n!的标准分解式,则
ai = 。 (1)
。 (1)
证明 对于任意固定的素数p,以p(k)表示在k的标准分解式中的p的指数,则
p(n!) = p(1) +p(2) +L+p(n)。
以nj表示p(1), p(2), L, p(n)中等于j的个数,那么
p(n!) = 1×n1+ 2×n2+ 3×n3+L, (2)
显然,nj就是在1, 2, L, n中满足pj½a并且pj + 1 a的整数a的个数,所以,由定理2有
a的整数a的个数,所以,由定理2有
nj = 。
。
将上式代入式(2),得到

即式(1)成立。证毕。
推论 设n是正整数,则
n! =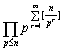 ,
,
其中 表示对不超过n的所有素数p求积。
表示对不超过n的所有素数p求积。
定理4 设n是正整数,1 £k£n - 1,则
 ÎN。 (3)
ÎN。 (3)
若n是素数,则n½ ,1 £k£n - 1。
,1 £k£n - 1。
证明 由定理3,对于任意的素数p,整数n!,k!与(n -k)!的标准分解式中所含的p的指数分别是
 。
。
利用定理1可知
 ,
,
因此 是整数。
是整数。
若n是素数,则对于1 £k £n - 1,有
(n, k!) = 1,(n, (n -k)!) = 1 Þ (n, k!(n -k)!) = 1,
由此及
 ÎN,
ÎN,
推出k!(n -k)!½(n - 1)!,从而n½ 。证毕。
。证毕。
例1 求最大的正整数k,使得10k½199!。
解 由定理3,199!的标准分解式中所含的5的幂指数是
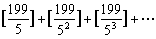 = 47,
= 47,
所以,所求的最大整数是k = 47。
例2 设x与y是实数,则
[2x] + [2y] ³ [x] + [x+y] + [y]。 (4)
解 设x = [x] +a,0 £a < 1,y = [y] +b,0 £b < 1,则
[x] + [x+y] + [y] = 2[x] + 2[y] + [a+b], (5)
[2x] + [2y] = 2[x] + 2[y] + [2a] + [2b]。 (6)
如果[a+b] = 0,那么显然有[a+b] £ [2a] + [2b];
如果[a+b] = 1,那么a与b中至少有一个不小于 ,于是
,于是
[2a] + [2b]³ 1 = [a+b]。
因此无论[a+b] = 0或1,都有[a+b] £ [2a] + [2b],由此及式(5)和式(6)可以推出式(4)。
例3 设n是正整数,则
 。 (7)
。 (7)
解 首先,我们有

所以
 。
。
若上式中的等号不成立,即
 , (8)
, (8)
则存在整数a,使得
 ,
,
因此

(2n+ 1)2- 1< (a2- 2n- 1)2£ (2n+ 1)2,
所以
a2- 2n - 1 = 2n + 1 Þ a2 = 4n+ 2。 (9)
但是,无论2½a或2 a,式(9)都不能成立,这个矛盾说明式(8)不能成立,即式(7)成立。
a,式(9)都不能成立,这个矛盾说明式(8)不能成立,即式(7)成立。
例4 设x是正数,n是正整数,则
 = [nx]。
= [nx]。
解 设x = [x] +a,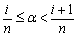 ,0 £i£n - 1,则
,0 £i£n - 1,则

= n[x] +i = n[x] + [na] = [n([x] +a)] = [nx]。
例5 求[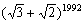 ]的个位数。
]的个位数。
解 由 得
得
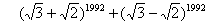
=
=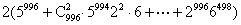
= 10A+ 2997×6498 = 10A+ 2×24498= 10A+ 2(25- 1)498
= 10B+ 2, (10)
其中A和B都是整数。由于0 < 5- < 1,所以,由式(10)可知[
< 1,所以,由式(10)可知[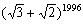 ]的个位数是1。
]的个位数是1。
注:一般地,如果A,BÎN,A2 > B, < 1,则由
< 1,则由

可以求出[ ]。
]。
例6 设x和y是正无理数, ,证明:数列
,证明:数列
[x], [2x], L, [kx], L与 [y], [2y], L, [my], L (11)
联合构成了整个正整数集合,而且,两个数列中的数互不相同。
解 显然x > 1,y > 1,并且x ¹y。因此,在数列(11)中至多有一个数等于给定的正整数n,否则存在正整数k与m,使得
n = [kx] = [my]。
因为x与y都是无理数,所以我们有
n < kx < n+ 1,n < my < n+ 1,

n < k+m < n+ 1,
这是不可能的。
下面证明,对于任意给定的正整数n,总可找到某个正整数k,使得n等于[kx]或者[ky]。假设不然,则存在p, qÎN,使得
[px] < n < [(p+ 1)x],[qy] < n < [(q+ 1)y]。
于是(因为x和y是无理数),
px < n < n+ 1 £ [(p+ 1)x] < (p+ 1)x,
qy < n < n+ 1 £ [(q+ 1)y] < (q+ 1)y,
 ,
,
p+q < n < n+ 1 < p+q+ 2,
这是不可能的。
习 题 七
1. 证明定理1。
2. 求使12347!被35k整除的最大的k值。
3. 设n是正整数,x是实数,证明: = n。
= n。
4. 设n是正整数,求方程
x2- [x2] = (x - [x])2
在[1, n]中的解的个数。
5. 证明:方程
f(x) = [x] + [2x] + [22x] + [23x] + [24x] + [25x] = 12345
没有实数解。
6. 证明:在n!的标准分解式中,2的指数h = n -k,其中k是n的二进制表示的位数码之和。
第八节 素 数
在第六节中我们已经证明了:每个正整数可以表示成素数幂的乘积。这就引出了一个问题:素数是否有无穷多个?如果有无穷多个,那么,作为无穷大量,素数个数具有怎样的性状?这是数论研究中的一个中心课题。本节要对这一问题作初步的研究。
定义1 对于正实数x,以p(x)表示不超过x的素数个数。
例如,p(15) = 6,p(10.4) = 4,p(50) = 15。
定理1 素数有无限多个。
证明 我们给出三个证明方法。
证法Ⅰ 假设只有k个素数,设它们是p1, p2, L, pk。记
N = p1p2Lpk+ 1。
由第一节定理2可知,N有素因数p,我们要说明p ¹pi,1 £i £k,从而得出矛盾。
事实上,若有某个i,1 £i £k,使得p = pi,则由
p½N = p1p2Lpk+ 1
推出p½1,这是不可能的。因此在p1, p2, L, pk之外又有一个素数p,这与假设是矛盾的。所以素数不可能是有限个。
证法Ⅱ 我们证明整数

是两两互素的,从而由第六节引理1可知素数有无限多个。
事实上,若m和n是整数,m > n ³ 0,则

此处Q是整数。因此

故

证法Ⅲ 假设只有有限个素数p1, p2, L, pk。由第六节定理1,每个正整数可以写成
n = ,ai³ 1,1 £i£k。
,ai³ 1,1 £i£k。
由于
 ,
,
所以,对于任何正整数N,有
 。
。
当N®¥时,上式左端是一个无穷大量,右端是有限的,这个矛盾说明素数不能是有限多个。证毕。
注1:形如 (n = 0, 1, 2, L)的数称为Fermat数。Fermat曾经猜测它们都是素数。这是错误的,因为尽管F0,F1,F2,F3,F4都是素数,F5 =
(n = 0, 1, 2, L)的数称为Fermat数。Fermat曾经猜测它们都是素数。这是错误的,因为尽管F0,F1,F2,F3,F4都是素数,F5 = 却是合数。
却是合数。
注2:将全体素数按大小顺序排列为
p1 = 2,p2 = 3,p3 = 5,p4,L,pn,L,
那么由第一个证明方法可以看出
pn + 1£p1p2Lpn+ 1,n ³ 1。
定理2 对于n³ 1,
(ⅰ) p(n) ³ log2n;
log2n;
(ⅱ) pn£ 22n。
证明 (ⅰ) 设n是大于1的正整数。由算术基本定理,对于任意的整数k,1 £k £n,都有整数a和b,使得k = a2b,其中整数b不能被任何大于1的整数的平方整除。现在,我们来看使得
k = a2b,1 £k £n (1)
即1 £a2b £n成立的整数a,b有多少对。首先,整数a的个数£ ;其次,由于b £ n并且不含有平方因数,所以,整数b的因数只可能是不超过n的不同的素数的乘积,因此,整数b的个数£ 2p(n)。这样,使得式(1)成立的整数a和b至多是
;其次,由于b £ n并且不含有平方因数,所以,整数b的因数只可能是不超过n的不同的素数的乘积,因此,整数b的个数£ 2p(n)。这样,使得式(1)成立的整数a和b至多是 2p(n)对,所以,n£
2p(n)对,所以,n£ 2p(n),即p(n) ³
2p(n),即p(n) ³ log2n。
log2n。
(ⅱ) 以pm表示第m个素数,在结论(ⅰ)中取n = pm,我们得到m³ log2pm,由此即可得到结论(ⅱ)。证毕。
log2pm,由此即可得到结论(ⅱ)。证毕。
注:定理2对于无穷大量p(x)的下界估计是相当粗糙的。下面的定理是已经知道的(由于其证明较繁,故本书中不予证明)。
定理3(素数定理) 我们有
p(x) ~ ,(x®¥),
,(x®¥),
此处logx是以e为底的x的对数。
推论 以pn表示第n个素数,则
pn~nlogn(n®¥)。
证明 由定理3,当n®¥时,有
n ~ 。 (2)
。 (2)
因此
nlogpn~pn,
logn+ loglogpn~ logpn,
logn ~ logpn。
由上式与式(2)得pn~nlogn(n®¥)。证毕。
例1 若a > 1,an- 1是素数,则a = 2,并且n是素数。
解 若a > 2,则由
an- 1 = (a - 1)(an - 1+an - 2+L+ 1)
可知an- 1是合数。所以a = 2。
若n是合数,则n = xy,x > 1,y >1,于是由
2xy- 1 = (2x- 1)(2x(y - 1)+ 2x(y - 2)+L+ 1)
以及2x- 1 > 1可知2n- 1是合数,所以2n- 1是素数时,n必是素数。
注:若n是素数,则称2n- 1是Mersenne数。
例2 形如4n+ 3的素数有无限多个。
解 若不然,假设只有k个形如4n+ 3的素数p1, p2, L, pk。记
N = 4p1pLpk – 1。
由第六节引理1,正整数N可以写成若干个素数之积。我们指出,这些素因数中至少有一个是4n+ 3形式。否则,若它们都是4n+ 1的形式,则N也是4n+ 1的形式,这与N的定义矛盾。以p表示这个素因数,则p ¹pi,1 £i £k。否则若有某个i,1 £i £k,使得p = pi,则由p½N推出p½1,这是不可能的。因此在p1, p2, L, pk之外又存在一个形如4n+ 3的素数p,这与原假设矛盾,所以形如4n+ 3的素数有无限多个。
例3 设f(x) = akxk+ak - 1xk - 1+L+a0是整系数多项式,那么,存在无穷多个正整数n,使得f(n)是合数。
解 不妨假定ak > 0。于是f(x)®+¥(x®+¥),因此,存在正整数N,使得当n > N时,有f(n) > 1。取整数x > N,记
y = f(x) = akxk+ak - 1xk - 1 +L+a0,
又设r是任意的正整数,n = ry+x,则
f(n) = f(ry+x) = ak(ry+x)k+ak - 1(ry+x)k - 1 +L+a0
= yQ+f(x) = y(Q+ 1)
是合数。
习 题 八
1. 证明:若2n+ 1是素数,则n是2的乘幂。
2. 证明:若2n- 1是素数,则n是素数。
3. 证明:形如6n+ 5的素数有无限多个。
4. 设d是正整数,6 d,证明:在以d为公差的等差数列中,连续三项都是素数的情况最多发生一次。
d,证明:在以d为公差的等差数列中,连续三项都是素数的情况最多发生一次。
5. 证明:对于任意给定的正整数n,必存在连续的n个自然数,使得它们都是合数。
6. 证明:级数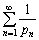 发散,此处使用了定理1注2中的记号。
发散,此处使用了定理1注2中的记号。
- 教案范本
-
教案范文
写教案的具体内容包括以下十项一课题说明本课名称二教学目的或称教学要求或称教学目标说明本课所要完成的教学任务三课型说明属新授课还是复…
-
小学语文教案范例
人民教育出版社三年级上册陶罐和铁罐教学设计小学姓名备注黑体字带部分为解释说明部分教学目标1会认10个生字会写14个生字正确读写生词…
-
(详细的教案范本)我们身边的线条
美术教案我们身边的线条我们身边的线条教学理念中小学美术教学大纲的修订具有划时代的意义它为学校美术教育拓展了博大的空间为中小学美术教…
-
教案基本格式及范例
教案基本格式及范例一教案基本格式1首页主要包括课程名称授课对象年级专业层次课型学时授课题目基本教材或参考书教学目的与要求授课内容与…
-
丁家沟小学营养餐满意度调查总结
为切实改善我校学生的营养状况,提高学生的身体健康水平,使营养餐更能适合学生口味,更能受到全体学生青睐。11月x日,我校按照安国乡学…
-
红歌大合唱活动总结
活动时间:20xx年x月x日活动地点:宁夏理工学院体育场主办单位:建环学院团总支红歌大合唱活动工作总结5月x日的“红歌大合唱”活动…
-
唱红歌活动总结
竹园小学唱红歌活动总结20xx年x月x日下午,我校成功开展了生动活泼“红歌大家唱”活动,全体师生都踊跃上台表演。演唱会以独唱、对唱…
-
经贸局机关支部工作总结
临渭区经贸局机关支部工作总结一年来,机关支部在局党委及机关工委的支持与指导下,以邓小平理论、“三个代表”重要思想及“十七”大精神为…
-
经验教训总结
最主要的问题怕而不果断雷曼光电当日放量涨停突破怕高而没敢追形态正好符合我的买点40%到手的利润没抓到当时听信了股评家说欧洲债务危机…