数学教学中学生反思意识的培养

一、问题的提出：

“反思”在当代认知心理学中，属于元认识的范畴，它是指对自身的思维过程、思维结果进行再认知和检验的过程，是学生调控学习的基础，是认知过程中强化自我意识、进行自我监控、自我调节的主要形式，是通过对数学学习活动过程的反思来进行数学学习。这是一种有效的学习方式，它的基本特征是探究性，即在考察学生学习活动的经历中探究其中的问题和答案，重构自己的理解，激活个人的智慧，并在活动中涉及的各个方向的相互作用下，产生超越已有信息之外的信息，从而帮助学生学会学习，使他们的学习活动成为一种有目标、有策略的主动行为，不断提出问题，发现有创意的新知识、新方法，尤其是当前把创新意识和问题解决的能力作为衡量和评价学生成绩优劣的标准时，更应该重视对学生反思意识的培养。

波利亚在《怎样解题》一书中指出：“即使是相当好的学生，当他得到问题的解答，并且很干净利落地写下论证后，就会合上书本，找点别的事来做，这样他们就错过了解题的一个重要而有教益的方面。通过回顾所完成的解答，通过重新检查这个结果和得出这一结果的路子，学生们可以巩固他们的知识和发展他们的解题能力。”目前数学教学中最薄弱的也正是数学学习过程中的反思环节，“反思型的教师教的学生才是反思型的学生”，因此。作为数学教师首先要有反思意识，改变传统数学教育教学观念，充分发挥学生在学习活动中的主体作用，有意识地引导学生进行反思，进一步为学生良好的个性品质的形成创造条件。

二、培养学生反思意识的重要性：

荷兰著名数学教育家费赖登塔尔指出：反思是数学思维活动的核心和动力。引导学生反思能促使他们从新的角度、多层次、多侧面地对问题及解决问题的思维过程进行全面的考察、分析和思考，从而进一步深化对问题的理解，揭示问题本质，探索一般规律，并使之产生新的发现。通过反思可以提高数学意识、优化思维品质；通过反思可以沟通新旧知识的联系，促进知识的同化和迁移，提高学习效率；通过反思可以拓宽思路、优化解法、完善学习活动中的积极性和主动性，促进学生的学习活动成为一种有目标、有策略的主动行为，不断的发现问题、提出问题，从而有效地培养学生勇于探索、勇于创新的精神。

当今社会呼唤新型的人才，如何在基础教育阶段培养学生的创新意识和创新精神是当今教育研究的重点和热点，中学数学教育从何寻找突破口？目前公认的一种观点是优化学生的思维品质，而反思意识恰恰是思维品质的综合体现。因此，中学数学教学中，注意培养学生的反思意识，具有重要的现实意义。反思在数学活动中越来越受到重视，那么如何引导学生学会反思呢？

三、培养学生反思意识的途径：

1、创设情境，引发学生反思意识

现代建构主义理论认为：数学学习不是一种授予—吸收的过程，而是学习者主动的建构活动；教师不应被看作“知识的授予者“，而应当成为学生活动的促进者。课堂教学中要善于创设情境，引发学生强烈的认知冲突，才能激发学生的反思意识。为此，教师要善于设疑，从学生的角度出发，从学生容易忽视的重要环节中提炼问题，然后通过环环相扣深入研究，并引导学生进行反思。

例1、  设x₁，x₂是方程2x²–4mx+（5m²–9m–12）=0，求x₁²+x₂²的最大值。

解：由题意知：x₁+x₂=2m， x₁ x₂=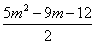 

      所以：x₁²+x₂²=–m²+9m+12=–（m–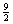）²+

则x₁²+x₂²的最大值为。上述解答看起来条理清楚，推理过程步步有据，解答结果似乎正确。引导学生反思解题过程，不难发现解答中没有考虑韦达定理应在△≥0时才能应用，由此找出错因，此题应△≥0的前提下，先确定m的取值范围，进而转化为二次函数在给定区间上求最大值的问题。通过反思，优化了学生的数学思维品质，培养了学生思维的严谨性和批判性，提高了学生解题的准备性。

2、在数学概念教学中，培养学生反思意识

教材中概念、公式、定理等显然是一些语言、符号，但他们都代表了确定的意义，是学生学习的主要知识点，也是思维的细胞，学生要获得概念、定理、公式的意义，靠死记硬背是很难牢固掌握的。因此，教师在教学中除了要引导学生积极参与概念、定理、公式、法则的发生和形成过程中来外，还应引导学生运用已有经验、知识、方法对所学的内容进行反思，多问几个为什么，只有通过反思，才能深刻理解其内涵和外延，揭示其本质，以免思维产生负迁移。

3、在解题教学中，培养学生的反思意识

在解题教学中，学生做完一道题后，引导学生进行反思，这不仅是解题的回顾或体验，而是引导学生根据问题的结构特点，通过对解题规律、解题思路、解题规律、解题途径的反思来进一步揭示数学问题的思维过程，开发学生的解题智慧，掌握规律，形成知识的正迁移，达到举一反三，触类旁通的目的。

（1）、反思解题规律

同一类型的问题，解题方法往往有其内在的规律性。因此，当一个问题解决后，要不失时机地引导学生反思解题方法，认真总结解题规律，力图从解决问题中找出普遍适用的东西，以现在的解题经验帮助今后的问题解决，提高解题能力。

例2：已知a_n分为等差数列，首项a₁,公差为d，求其通项公式。

解：∵a_n为等差数列∴a_n-a_n–1=d(n≥2)

由a_n=(a_n –a_n–1)+( a_n–2–a_n–3)+……+( a₃–a₂)+( a₂–a₁)+ a₁

   =d+d+d+……+d+a₁

     = a₁+(n–1)d

   反思1：a_n –a_n–1=d, 可知a_n= a₁+(n–1)d

若a_n –a_n–1=n , a₁=1, 求a_n的通项公式

解：由 a_n=(a_n –a_n–1)+( a_n–2–a_n–3)+……+( a₃–a₂)+( a₂–a₁)+ a₁

         =n+(n–1)+(n–2)+ ……+3+2+1

         =

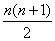
反思2：若数列{ a_n }，已知a₁和a_n –a_n–1=f(n)

则可用累加法求数列的通项。

反思3：若已知a₁=1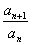，=n，怎样求a_n的通项公式

由反思2的启示，后一项与前一项的差为一个关于n的函数。可用累加法去求数列的通项，后一项与前一项的商为一个关于n的函数，是否可用累乘法呢？尝试：由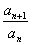=n得a_n=·……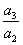··a₁= n (n–1) (n–2)……3·2·1=n！

通过以上反思，引导学生归纳出那种类数列的通项可累加法或累乘法去完成。由此得到一类问题的解决的办法，这有利于培养学生深入钻研的良好习惯，从而进一步激发学生的求知欲及创新精神。

（2）反思解题思路

在解完一道题后，引导学生对解题思路进行反思，看能否根据该题的特点进行多角度的思考、联想，找寻各种思路，这有助于培养学生思维的广阔性。

例3、已知a²+b²=16，求a+b的最大值和最小值。

 解：设a=4sinθ b=4cosθ

则a+b=4 sinθ+4cosθ=4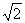 sin（θ+）

∴（a+b）_max=4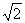

   （a+b）_min=－4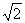

反思本题的解题路，还可以找到以下各种解法：

解法二：（基本不等式）

∵（a+b）²= a²+b²+2ab≤a²+b² + a²+b²=32

∴│a+b│≤4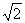

即（a+b）_max=4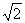  （a+b）_min=－4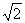

解法三：（判别式法）

设a+b=m  b=m－a 代入a²+b²=16可得

2a²－2 ma+ m²－16=0  由△=4 m²－4X2（m²－16）≥0

可得m²≤32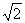  ∴－4≤m≤4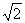

即（a+b）_max=4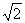   （a+b）_min=－4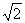

解法4：（线性规划法）

设z= a+b   a²+b²=16，表示的平面区域是圆，作直线l: a+b=0把直线l向右上方平移至与a²+b²=16相切的切线处时，求得切点M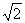（2，2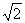），这时（a+b）_max=4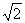

同理，把L向右下方移至与圆相切时，可得

（a+b）_min=－4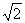

解题时仔细分析题目的条件及关系，多角度联想，寻求一题多解、一题巧解，优化思维，灵感的产生来源于扎实的基础，简捷的方法来自于丰富的联想。

（3）反思解题过程

在解完一道题后，引导学生对解题过程进行反思，看看有没有思维回路，哪些过程可以省略，哪些过程可以合并，哪些过程不够严谨，以培养学生思维的合理性、条理性、敏捷性。

例4、已知x＞0求函数y=x+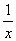的最小值

解法1：运用基本不等式

∵x+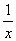≥2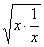（当时取x =1时，取“=”号）

∴y _min =2

反思1：引导学生总结运用基本不等式的条件“一正、二定、三相等”，加深对基本不等式的理解。

反思2：启发学生探讨其它解法，培养学生思维的发散性，掌握解决此类问题的基本方法。

解法2：运用函数单调性，函数y=x+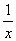在（0，1）是减函数，在（1，+∞）上是增函数。

∴x=1时，y _min=2

解法3：换元法

令x=tan (0＜＜）

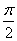则y= tan +

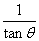
    =1+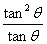

    =

∵0＜θ ＜

∴0＜≤1

∴=1时，即时，y _min=2

反思3：变题，提高学生灵活运用能力

变题1：已知x≥3时，求函数x+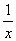的最小值

分析：x≥3时，在x+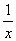≥2中，等号不成立，故本题不适宜用基本不等式解，可用函数单调性，易证y=x+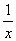在（3，∞）上单调递增，所以当x≥3时，y _min=

变题2：已知x＞1，求y= x+ 的最小值

解：∵y=（x－1）+ +1 且x－1＞0

∴y≥3 即当x=2时，y _min=3

总之，在数学教学中，教师要善于引导学生反思下列问题：

（1）、是否把握了与问题有关的知识结构？是否达到了通过练习掌握知识的目的？

（2）、解题方法是否正确，圆满？有无增、漏、错等情况？

（3）、此题的解题思路中关键的是哪几步？是如何归纳的？

（4）、此题还有没有别的解法？有无更好的解法？

（5）、此题和以前的哪些题目是类似的，此题的解题规律是什么？

（6）、此题是否能进行变式、引伸和推广？

（7）、解题中运用了哪些数学思想方法？

在数学教学中，如果教师不失时机地引导学生进行反思，培养学生的反思意识，那么学生的思维就会更开阔、更灵活，见解更深刻、更新颖，也会大大提高学生提出问题、分析问题、解决问题的能力，进一步促进学生数学方面的发展，真正实现新课改的理念：“人人学有价值的数学；人人都获得必须的数学；不同的人在数学上有不同的发展。”

参考文献：

1、    涂荣豹《试论反思性数学学习》数学教育学报  20##年4月

2、          任樟辉《数学思维论》                     20##年12月

3、          袁晓松《元认知与认知策略的迁移》         1991年8月

4、          熊川武《反思性教学》 华东师范大学出版社  1999年6月

5、          杨世明著：《MM教育方式理论与实践》        20##年7月

 

第二篇：数学教学中学生反思意识的培养

数学教学中学生反思意识的培养

习水县三岔河中学：袁必军

一、问题的提出：

“反思”在当代认知心理学中，属于元认识的范畴，它是指对自身的思维过程、思维结果进行再认知和检验的过程，是学生调控学习的基础，是认知过程中强化自我意识、进行自我监控、自我调节的主要形式，是通过对数学学习活动过程的反思来进行数学学习。这是一种有效的学习方式，它的基本特征是探究性，即在考察学生学习活动的经历中探究其中的问题和答案，重构自己的理解，激活个人的智慧，并在活动中涉及的各个方向的相互作用下，产生超越已有信息之外的信息，从而帮助学生学会学习，使他们的学习活动成为一种有目标、有策略的主动行为，不断提出问题，发现有创意的新知识、新方法，尤其是当前把创新意识和问题解决的能力作为衡量和评价学生成绩优劣的标准时，更应该重视对学生反思意识的培养。

波利亚在《怎样解题》一书中指出：“即使是相当好的学生，当他得到问题的解答，并且很干净利落地写下论证后，就会合上书本，找点别的事来做，这样他们就错过了解题的一个重要而有教益的方面。通过回顾所完成的解答，通过重新检查这个结果和得出这一结果的路子，学生们可以巩固他们的知识和发展他们的解题能力。”目前数学教学中最薄弱的也正是数学学习过程中的反思环节，“反思型的教师教的学生才是反思型的学生”，因此。作为数学教师首先要有反思意 1

识，改变传统数学教育教学观念，充分发挥学生在学习活动中的主体作用，有意识地引导学生进行反思，进一步为学生良好的个性品质的形成创造条件。

二、培养学生反思意识的重要性：

荷兰著名数学教育家费赖登塔尔指出：反思是数学思维活动的核心和动力。引导学生反思能促使他们从新的角度、多层次、多侧面地对问题及解决问题的思维过程进行全面的考察、分析和思考，从而进一步深化对问题的理解，揭示问题本质，探索一般规律，并使之产生新的发现。通过反思可以提高数学意识、优化思维品质；通过反思可以沟通新旧知识的联系，促进知识的同化和迁移，提高学习效率；通过反思可以拓宽思路、优化解法、完善学习活动中的积极性和主动性，促进学生的学习活动成为一种有目标、有策略的主动行为，不断的发现问题、提出问题，从而有效地培养学生勇于探索、勇于创新的精神。

当今社会呼唤新型的人才，如何在基础教育阶段培养学生的创新意识和创新精神是当今教育研究的重点和热点，中学数学教育从何寻找突破口？目前公认的一种观点是优化学生的思维品质，而反思意识恰恰是思维品质的综合体现。因此，中学数学教学中，注意培养学生的反思意识，具有重要的现实意义。反思在数学活动中越来越受到重视，那么如何引导学生学会反思呢？

2

三、培养学生反思意识的途径：

1、创设情境，引发学生反思意识

现代建构主义理论认为：数学学习不是一种授予—吸收的过程，而是学习者主动的建构活动；教师不应被看作“知识的授予者“，而应当成为学生活动的促进者。课堂教学中要善于创设情境，引发学生强烈的认知冲突，才能激发学生的反思意识。为此，教师要善于设疑，从学生的角度出发，从学生容易忽视的重要环节中提炼问题，然后通过环环相扣深入研究，并引导学生进行反思。

例1、 设x1，x2是方程2x2–4mx+（5m2–9m–12）=0，求x12+x22

的最大值。

5m2?9m?12解：由题意知：x1+x2=2m， x1 x2= 2

所以：x122+x22=–m2+9m+12=–（m–9

）+ 129 4

则x12+x22的最大值为129。上述解答看起来条理清楚，推理过程步步4

有据，解答结果似乎正确。引导学生反思解题过程，不难发现解答中没有考虑韦达定理应在△≥0时才能应用，由此找出错因，此题应△≥0的前提下，先确定m的取值范围，进而转化为二次函数在给定区间上求最大值的问题。通过反思，优化了学生的数学思维品质，培养了学生思维的严谨性和批判性，提高了学生解题的准备性。

2、在数学概念教学中，培养学生反思意识

教材中概念、公式、定理等显然是一些语言、符号，但他们都代 3

表了确定的意义，是学生学习的主要知识点，也是思维的细胞，学生要获得概念、定理、公式的意义，靠死记硬背是很难牢固掌握的。因此，教师在教学中除了要引导学生积极参与概念、定理、公式、法则的发生和形成过程中来外，还应引导学生运用已有经验、知识、方法对所学的内容进行反思，多问几个为什么，只有通过反思，才能深刻理解其内涵和外延，揭示其本质，以免思维产生负迁移。

3、在解题教学中，培养学生的反思意识

在解题教学中，学生做完一道题后，引导学生进行反思，这不仅是解题的回顾或体验，而是引导学生根据问题的结构特点，通过对解题规律、解题思路、解题规律、解题途径的反思来进一步揭示数学问题的思维过程，开发学生的解题智慧，掌握规律，形成知识的正迁移，达到举一反三，触类旁通的目的。

（1）、反思解题规律

同一类型的问题，解题方法往往有其内在的规律性。因此，当一个问题解决后，要不失时机地引导学生反思解题方法，认真总结解题规律，力图从解决问题中找出普遍适用的东西，以现在的解题经验帮助今后的问题解决，提高解题能力。

例2：已知an分为等差数列，首项a1,公差为d，求其通项公式。

解：∵an为等差数列∴an-an–1=d(n≥2)

由an=(an –an–1)+( an–2–an–3)+??+( a3–a2)+( a2–a1)+ a1

4

=d+d+d+??+d+a1

= a1+(n–1)d

反思1：an –an–1=d, 可知an= a1+(n–1)d

若an –an–1=n , a1=1, 求an的通项公式

解：由 an=(an –an–1)+( an–2–an–3)+??+( a3–a2)+( a2–a1)+ a1 =n+(n–1)+(n–2)+ ??+3+2+1 =

n(n?1)

2

反思2：若数列{ an }，已知a1和an –an–1=f(n) 则可用累加法求数列的通项。 反思3：若已知a1=1，

an?1

=n，怎样求an的通项公式 an

由反思2的启示，后一项与前一项的差为一个关于n的函数。可用累加法去求数列的通项，后一项与前一项的商为一个关于n的函数，是否可用累乘法呢？尝试：由

an?1aaaa

=n得an=nn?1??32·a1= anan?1an?2a2a1

n (n–1) (n–2)??3·2·1=n！

通过以上反思，引导学生归纳出那种类数列的通项可累加法或累乘法去完成。由此得到一类问题的解决的办法，这有利于培养学生深入钻研的良好习惯，从而进一步激发学生的求知欲及创新精神。 （2）反思解题思路

在解完一道题后，引导学生对解题思路进行反思，看能否根据该

5

题的特点进行多角度的思考、联想，找寻各种思路，这有助于培养学生思维的广阔性。

例3、已知a2+b2=16，求a+b的最大值和最小值。

解：设a=4sinθ b=4cosθ

则a+b=4 sinθ+4cosθ=42 sin（θ+

∴（a+b）max=42

（a+b）min=－42 ?） 4

反思本题的解题路，还可以找到以下各种解法：

解法二：（基本不等式）

∵（a+b）2= a2+b2+2ab≤a2+b2 + a2+b2=32

∴│a+b│≤42

即（a+b）max=42 （a+b）min=－42

解法三：（判别式法）

设a+b=m b=m－a 代入a2+b2=16可得

2a2－2 ma+ m2－16=0 由△=4 m2－4X2（m2－16）≥0

可得m2≤32 ∴－42≤m≤42

即（a+b）max=42 （a+b）min=－42

解法4：（线性规划法）

设z= a+b a2+b2=16，表示的平面区域是圆，作直线l: a+b=0把直线l向右上方平移至与a2+b2=16相切的切线处时，求得切点M（22，22），这时（a+b）max=42

6

同理，把L向右下方移至与圆相切时，可得

（a+b）min=－42

解题时仔细分析题目的条件及关系，多角度联想，寻求一题多解、一题巧解，优化思维，灵感的产生来源于扎实的基础，简捷的方法来自于丰富的联想。

（3）反思解题过程

在解完一道题后，引导学生对解题过程进行反思，看看有没有思维回路，哪些过程可以省略，哪些过程可以合并，哪些过程不够严谨，以培养学生思维的合理性、条理性、敏捷性。

例4、已知x＞0求函数y=x+的最小值

解法1：运用基本不等式

∵x+≥2x?（当时取x =1时，取“=”号）

∴y min =2

反思1：引导学生总结运用基本不等式的条件“一正、二定、三相等”，加深对基本不等式的理解。

反思2：启发学生探讨其它解法，培养学生思维的发散性，掌握解决此类问题的基本方法。

解法2：运用函数单调性，函数y=x+在（0，1）是减函数，在（1，+∞）上是增函数。

∴x=1时，y min=2 1x1x1x1x

7

解法3：换元法

令x=tan ?(0＜?＜）

则y= tan ?+ 1 tan??2

tan2? =1+ tan?

= 2 sin?

∵0＜θ ＜?

∴0＜sin?≤1

∴sin?=1时，即???

2时，y min=2

反思3：变题，提高学生灵活运用能力

变题1：已知x≥3时，求函数x+的最小值

分析：x≥3时，在x+≥2中，等号不成立，故本题不适宜用基本不等式解，可用函数单调性，易证y=x+在（3，∞）上单调递增，所以当x≥3时，y min= 10 3

1的最小值 x?11x1x1x变题2：已知x＞1，求y= x+

解：∵y=（x－1）+ 1+1 且x－1＞0 x?1

∴y≥3 即当x=2时，y min=3

总之，在数学教学中，教师要善于引导学生反思下列问题：

（1）、是否把握了与问题有关的知识结构？是否达到了通过练习掌握知识的目的？

（2）、解题方法是否正确，圆满？有无增、漏、错等情况？ 8

（3）、此题的解题思路中关键的是哪几步？是如何归纳的？

（4）、此题还有没有别的解法？有无更好的解法？

（5）、此题和以前的哪些题目是类似的，此题的解题规律是什么？

（6）、此题是否能进行变式、引伸和推广？

（7）、解题中运用了哪些数学思想方法？

在数学教学中，如果教师不失时机地引导学生进行反思，培养学生的反思意识，那么学生的思维就会更开阔、更灵活，见解更深刻、更新颖，也会大大提高学生提出问题、分析问题、解决问题的能力，进一步促进学生数学方面的发展，真正实现新课改的理念：“人人学有价值的数学；人人都获得必须的数学；不同的人在数学上有不同的发展。”

参考文献：

1、 涂荣豹《试论反思性数学学习》数学教育学报 20xx年4月

2、 任樟辉《数学思维论》 20xx年12月

3、 袁晓松《元认知与认知策略的迁移》 19xx年8月

4、 熊川武《反思性教学》 华东师范大学出版社 19xx年6月

5、 杨世明著：《MM教育方式理论与实践》 20xx年7月 9