高一数学知识总结必修一 一
高一数学知识总结必修一 一,集合 一,集合有关概念 1. 集合的含义 2. 集合的中元素的三个特性: (1)元素的确定性如:世界上最高的山 (2)元素的互异性如: HAPPY 的字母组成的集合{H,A,P,Y} 由 (3)元素的无序性: 如:{a,b,c}和{a,c,b}是表示同一个集 合 3.集合的表示:{ … } 如:{我校的篮球队员},{太平洋, 大西洋,印度洋,北冰洋} (1)用 拉 丁 字 母 表 示 集 合 : A={ 我 校 的 篮 球 队 员},B={1,2,3,4,5} (2)集合的表示方法:列举法与描述法. 注意:常用数集及其记法: 非负整数集(即自然数集) 记作:N 正整数集 N*或 N+ 整数集 Z 有理数集 Q 实数集 R 1)列举法:{a,b,c……} 2)描述法:将集合中的元素的公共属性描述出来,写在大 括号内表示集合的方法.{x∈R| x-3>2} ,{x| x-3>2} 3)语言描述法:例:{不是直角三角形的三角形} 4)Venn 图: 4,集合的分类: (1)有限集 含有有限个元素的集合 (2)无限集 含有无限个元素的集合 2 (3)空集 不含任何元素的集合 例:{x|x =-5} 二,集合间的基本关系 1."包含"关系—子集 注意: A B 有两种可能(1)A 是 B 的一部分,(2)A 与 ; B 是同一集合. 反之: 集合 A 不包含于集合 B,或集合 B 不包含集合 A,记作 / / AB 或 BA 2. "相等"关系:A=B (5≥5,且 5≤5,则 5=5) 实例:设 A={x|x2-1=0} B={-1,1} "元素相同则两集 合相等" 即:① 任何一个集合是它本身的子集.AA ②真子集:如果 AB,且 A≠ B 那就说集合 A 是集合
B 的真子 集,记作 A B(或 B A) ③如果 AB, BC ,那么 AC ④ 如果 AB 同时 BA 那么 A=B 3. 不含任何元素的集合叫做空集,记为Φ 规定: 空集是任何集合的子集, 空集是任何非空集合的真 子集. n n-1 有 n 个元素的集合,含有 2 个子集,2 个真子集 二,函数 1,函数定义域,值域求法综合 2.,函数奇偶性与单调性问题的解题策略 3,恒成立问题的求解策略 4,反函数的几种题型及方法 5,二次函数根的问题——一题多解 &指数函数 y=a^x a^a*a^b=a^a+b(a>0,a,b 属于 Q) (a^a)^b=a^ab(a>0,a,b 属于 Q) (ab)^a=a^a*b^a(a>0,a,b 属于 Q) 指数函数对称规律: 1,函数 y=a^x 与 y=a^-x 关于 y 轴对称 2,函数 y=a^x 与 y=-a^x 关于 x 轴对称 3,函数 y=a^x 与 y=-a^-x 关于坐标原点对称 &对数函数 y=loga^x 如果 a > 0 ,且 a ≠ 1 , M > 0 , N > 0 ,那么: 1 ○ log a ( M N ) = log a M + log a N ; M 2 ○ log a = log a M - log a N ; N 3 ○ log a M n = n log a M (n ∈ R ) . 注意:换底公式 log c b log a b = ( a > 0 , a ≠ 1; > 0 , c ≠ 1; > 0 ) 且 c 且 b . log c a 幂函数 y=x^a(a 属于 R) 1,幂函数定义:一般地,形如 y = x α (a ∈ R ) 的函数称为幂 函数,其中 α 为常数. 2,幂函数性质归纳. (1)所有的幂函数在(0,+∞)都有定义并且图象都过点 (1,1) ; (2)α > 0 时,幂函数的图象通过原点,并且在区间
[0,+∞) 上是增函数.特别地,当 α > 1 时,幂函数的图象下凸;当 0 < α < 1 时,幂函数的图象上凸; (3)α < 0 时, 幂函数的图象在区间 (0,+∞) 上是减函数. 在 第一象限内,当 x 从右边趋向原点时,图象在 y 轴右方无限 地逼近 y 轴正半轴,当 x 趋于 + ∞ 时,图象在 x 轴上方无限 地逼近 x 轴正半轴. 方程的根与函数的零点 1 , 函 数 零 点 的 概 念 : 对 于 函 数 y = f ( x)( x ∈ D ) , 把 使 f ( x) = 0 成立的实数 x 叫做函数 y = f ( x)( x ∈ D ) 的零点. 2, 函数零点的意义: 函数 y = f (x) 的零点就是方程 f ( x) = 0 实数根,亦即函数 y = f (x) 的图象与 x 轴交点的横坐标. 即: 方程 f ( x) = 0 有实数根 函数 y = f (x) 的图象与 x 轴有 交点 函数 y = f (x) 有零点. 3,函数零点的求法: 1 ○ (代数法)求方程 f ( x) = 0 的实数根; 2 ○ (几何法)对于不能用求根公式的方程,可以将它与函 数 y = f (x) 的图象联系起来,并利用函数的性质找出零点. 4,二次函数的零点: 二次函数 y = ax 2 + bx + c(a ≠ 0) . (1)△>0,方程 ax 2 + bx + c = 0 有两不等实根,二次函 数的图象与 x 轴有两个交点,二次函数有两个零点.
(2)△=0,方程 ax 2 + bx + c = 0 有两相等实根,二次函 二次函数有一个二重零点或二 数的图象与 x 轴有一个交点, 阶零点. (3)△<0,方程 ax 2 + bx + c = 0 无实根,二次函数的图象与 x 轴无交点,二次 函数无零点. 三,平面向量 向量:既有大小,又有方向的量. 数量:只有大小,没有方向的量. 有向线段的三要素:起点,方向,长度. 零向量:长度为 0 的向量. 单位向量:长度等于 1 个单位的向量. 相等向量:长度相等且方向相同 方向相同的向量 方向相同 &向量的运算 加法运算 AB+BC=AC,这种计算法则叫做向量加法的三角形法则. 已知两个从同
一点 O 出发的两个向量 OA, 以 OA, 为邻边作平行四边形 OACB, OB, OB 则以 O 为起点的对角线 OC 就是向量 OA,OB 的和,这种计算法则叫做向量加法的 平行四边形法则. 对于零向量和任意向量 a,有:0+a=a+0=a. |a+b|≤|a|+|b|. 向量的加法满足所有的加法运算定律. 减法运算 与 a 长度相等,方向相反的向量,叫做 a 的相反向量,-(-a)=a,零向量的相 反向量仍然是零向量. (1)a+(-a)=(-a)+a=0(2)a-b=a+(-b). 数乘运算 实数λ与向量 a 的积是一个向量,这种运算叫做向量的数乘,记作λa,|λa| =|λ||a|,当λ > 0 时,λa 的方向和 a 的方向相同,当λ < 0 时,λa 的方 向和 a 的方向相反,当λ = 0 时,λa = 0. 设λ,μ是实数,那么:(1)(λμ)a = λ(μa)(2)(λ μ)a = λa μa(3) λ(a ± b) = λa ± λb(4)(-λ)a =-(λa) = λ(-a). 向量的加法运算,减法运算,数乘运算统称线性运算. 向量的数量积 已知两个非零向量 a,b,那么|a||b|cos θ叫做 a 与 b 的数量积或内积,记作 a?b,θ是 a 与 b 的夹角,|a|cos θ(|b|cos θ)叫做向量 a 在 b 方向上(b 在 a 方向上)的投影.零向量与任意向量的数量积为 0. a?b 的几何意义: 数量积 a?b 等于 a 的长度|a|与 b 在 a 的方向上的投影|b|cos θ 的乘积. 两个向量的数量积等于它们对应坐标的乘积的和. 四,三角函数 1,善于用"1"巧解题 2,三角问题的非三角化解题策略 3,三角函数有界性求最值解题方法 4,三角函数向量综合题例析 5,三角函数中的数学思想方法 15,正弦函数,余弦函数和正切函数的图象与性质: 性 函 质 数 y = sin x y = cos x y = tan x 图 象 定 义 域 值 域 最 值 R R π x x ≠ kπ + , k ∈ Ζ 2 R 既无最大值也无最小 值 [ 1,1] 当 x = 2k π + [ 1,1] ( k ∈ Ζ) 当 x = 2kπ ( k ∈ Ζ ) 时, ymax = 1 ;当 x = 2kπ + π π 2 时 , ymax = 1 ; 当 x = 2k π π 2 ( k ∈ Ζ ) 时, ymin = 1 . 2π ( k ∈ Ζ ) 时, ymin = 1 . 周 期 性 奇 偶 性 2π π 奇函数 偶函数 奇函数 π π 在 2 kπ , 2 k π + 2 2 单 调 性 在 ( k ∈ Ζ ) 上是增函数;在 π 3π 2 kπ + 2 , 2 kπ + 2 π π 上 是 增 函 数 ; 在 在 kπ , kπ + 2 2 [ 2 kπ , 2 kπ + π ] ( k ∈ Ζ ) 上是增函数. ( k ∈ Ζ ) 上是减函数. [ 2 kπ π , 2 kπ ] ( k ∈ Ζ ) ( k ∈ Ζ ) 上是减函数. 对 称 中 心 对 称 中 心 对 ( kπ , 0 )( k ∈ Ζ ) 称 对 称 性 π x = kπ + ( k ∈ Ζ ) 2 对 称 中 心 轴 π kπ + , 0 ( k ∈ Ζ ) 2 对称轴 x = kπ ( k ∈ Ζ ) kπ , 0 (k ∈ Ζ) 2 无对称轴 { } 第二象限角的集合为 {α k 360 + 90 < k 360 + 180 , k ∈ Ζ} 第三象限角的集合为 {α k 360 + 180 < α < k 360 + 270 , k ∈ Ζ} 第四象限角的集合为 {α k 360 + 270 < α < k 360 + 360 , k ∈ Ζ} 终边在 x 轴上的角的集合为 {α α = k 180 , k ∈ Ζ} 终边在 y 轴上的角的集合为 {α α = k 180 + 90 , k ∈ Ζ} 终边在坐标轴上的角的集合为 {α α = k 90 , k ∈ Ζ} 第一象限角的集合为 α k 360 < α < k 360 + 90 , k ∈ Ζ 必修四 角 α 的顶点与原点重合,角的始边与 x 轴的非负半轴重合,终边落在第几象限, 则称 α 为第几象限角. 3,与角 α 终边相同的角的集合为 β β = k 360 + α , k ∈ Ζ 4,已知 α 是第几象限角,确定 { } ( n ∈ Ν* ) 所在象限的方法:先把各象限均分 n 等 n 份,再从 x 轴的正半轴的上方起,依次将各区域标上一,二,三,四,则 α 原来终边所落在的区域. n 5,长度等于半径长的弧所对的圆心角叫做 1 弧度. 口诀:奇变偶不变,符号看象限. 公式一: 设α为任意角,终边相同的角的同一三角函数的值相等: sin(2kπ+α)=sinα cos(2kπ+α)=cosα tan(2kπ+α)=tanα cot(2kπ+α)=cotα 公式二: 设α为任意角,π α的三角函数值与α的三角函数值之间的关系: sin(π+α)=-sinα cos(π+α)=-cosα tan(π+α)=tanα cot(π+α)=cotα 公式三: 任意角α与 -α的三角函数值之间的关系: sin(-α)=-sinα cos(-α)=cosα tan(-α)=-tanα cot(-α)=-cotα 公式四: 利用公式二和公式三可以得到π-α与α的三角函数值之间的关系: sin(π-α)=sinα cos(π-α)=-cosα tan(π-α)=-tanα cot(π-α)=-cotα 公式五: 利用公式一和公式三可以得到 2π-α与α的三角函数值之间的关系: sin(2π-α)=-sinα cos(2π-α)=cosα tan(2π-α)=-tanα cot(2π-α)=-cotα 是第几象限对应的标号即为 α α 公式六: π/2±α及 3π/2±α与α的三角函数值之间的关系: sin(π/2+α)=cosα cos(π/2+α)=-sinα tan(π/2+α)=-cotα cot(π/2+α)=-tanα sin(π/2-α)=cosα cos(π/2-α)=sinα tan(π/2-α)=cotα cot(π/2-α)=tanα sin(3π/2+α)=-cosα cos(3π/2+α)=sinα tan(3π/2+α)=-cotα cot(3π/2+α)=-tanα sin(3π/2-α)=-cosα cos(3π/2-α)=-sinα tan(3π/2-α)=cotα cot(3π/2-α)=tanα (以上 k∈Z) 其他三角函数知识: 同角三
角函数基本关系 ⒈同角三角函数的基本关系式 倒数关系: tanα cotα=1 sinα cscα=1 cosα secα=1 商的关系: sinα/cosα=tanα=secα/cscα cosα/sinα=cotα=cscα/secα 平方关系: sin^2(α)+cos^2(α)=1 1+tan^2(α)=sec^2(α) 1+cot^2(α)=csc^2(α) 两角和差公式 ⒉两角和与差的三角函数公式 sin(α+β)=sinαcosβ+cosαsinβ sin(α-β)=sinαcosβ-cosαsinβ cos(α+β)=cosαcosβ-sinαsinβ cos(α-β)=cosαcosβ+sinαsinβ tanα+tanβ tan(α+β)=—————— 1-tanα tanβ tanα-tanβ tan(α-β)=—————— 1+tanα tanβ 倍角公式 ⒊二倍角的正弦,余弦和正切公式(升幂缩角公式) sin2α=2sinαcosα cos2α=cos^2(α)-sin^2(α)=2cos^2(α)-1=1-2sin^2(α) 2tanα tan2α=————— 1-tan^2(α) 半角公式 ⒋半角的正弦,余弦和正切公式(降幂扩角公式) 1-cosα sin^2(α/2)=————— 2 1+cosα cos^2(α/2)=————— 2 1-cosα tan^2(α/2)=————— 1+cosα 万能公式 ⒌万能公式 2tan(α/2) sinα=—————— 1+tan^2(α/2) 1-tan^2(α/2) cosα=—————— 1+tan^2(α/2) 2tan(α/2) tanα=—————— 1-tan^2(α/2) 和差化积公式 ⒎三角函数的和差化积公式 α+β α-β sinα+sinβ=2sin—----cos—--2 2 α+β α-β sinα-sinβ=2cos—----sin—---2 2 α+β α-β cosα+cosβ=2cos—-----cos—----2 2 α+β α-β cosα-cosβ=-2sin—-----sin—----2 2 积化和差公式 ⒏三角函数的积化和差公式 sinα cosβ=0.5[sin(α+β)+sin(α-β)] cosα sinβ=0.5[sin(α+β)-sin(α-β)] cosα cosβ=0.5[cos(α+β)+cos(α-β)] sinα sinβ=- 0.5[cos(α+β)-cos(α-β)]
第二篇:高一数学知识点总结--必修5
高中数学必修5知识点
第一章:解三角形
1、正弦定理:在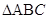 中,
中,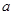 、
、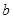 、
、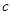 分别为角
分别为角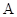 、
、 、
、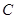 的对边,
的对边,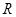 为
为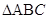 的外接圆的半径,则有
的外接圆的半径,则有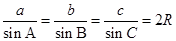 .
.
2、正弦定理的变形公式:①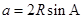 ,
,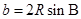 ,
,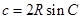 ;
;
② ,
,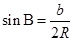 ,
, ;(正弦定理的变形经常用在有三角函数的等式中)
;(正弦定理的变形经常用在有三角函数的等式中)
③ ;
;
④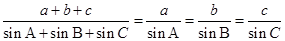 .
.
3、三角形面积公式: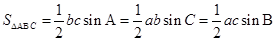 .
.
4、余 定理:在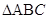 中,有
中,有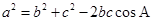 ,
,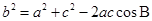 ,
,
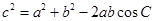 .
.
5、余弦定理的推论: ,
,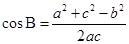 ,
,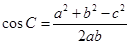 .
.
6、设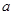 、
、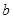 、
、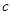 是
是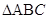 的角
的角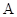 、
、 、
、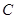 的对边,则:①若
的对边,则:①若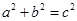 ,则
,则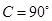 为直角三角形;
为直角三角形;
②若 ,则
,则 为锐角三角形;③若
为锐角三角形;③若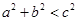 ,则
,则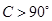 为钝角三角形.
为钝角三角形.
第二章:数列
1、数列:按照一定顺序排列着的一列数.
2、数列的项:数列中的每一个数.
3、有穷数列:项数有限的数列.
4、无穷数列:项数无限的数列.
5、递增数列:从第2项起,每一项都不小于它的前一项的数列.
6、递减数列:从第2项起,每一项都不大于它的前一项的数列.
7、常数列:各项相等的数列.
8、摆动数列:从第2项起,有些项大于它的前一项,有些项小于它的前一项的数列.
9、数列的通项公式:表示数列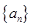 的第
的第 项与序号
项与序号 之间的关系的公式.
之间的关系的公式.
10、数列的递推公式:表示任一项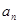 与它的前一项
与它的前一项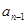 (或前几项)间的关系的公式.
(或前几项)间的关系的公式.
11、如果一个数列从第2项起,每一项与它的前一项的差等于同一个常数,则这个数列称为等差数列,这个常数称为等差数列的公差.
12、由三个数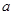 ,
,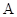 ,
,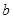 组成的等差数列可以看成最简单的等差数列,则
组成的等差数列可以看成最简单的等差数列,则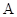 称为
称为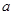 与
与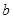 的等差中项.若
的等差中项.若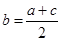 ,则称
,则称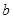 为
为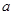 与
与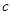 的等差中项.
的等差中项.
13、若等差数列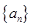 的首项是
的首项是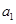 ,公差是
,公差是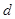 ,则
,则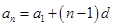 .
.
通项公式的变形:①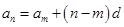 ;②
;②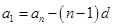 ;③
;③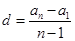 ;④
;④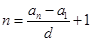 ;⑤
;⑤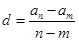 .
.
14、若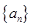 是等差数列,且
是等差数列,且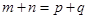 (
(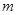 、
、 、
、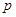 、
、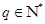 ),则
),则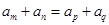 ;若
;若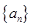 是等差数列,且
是等差数列,且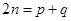 (
( 、
、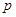 、
、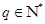 ),则
),则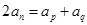 ;下角标成等差数列的项仍是等差数列;连续m项和构成的数列成等差数列。
;下角标成等差数列的项仍是等差数列;连续m项和构成的数列成等差数列。
15、等差数列的前 项和的公式:①
项和的公式:①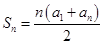 ;②
;②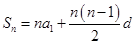 .
.
16、等差数列的前 项和的性质:①若项数为
项和的性质:①若项数为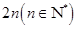 ,则
,则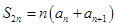 ,且
,且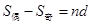 ,
,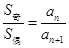 .②若项数为
.②若项数为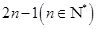 ,则
,则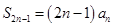 ,且
,且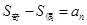 ,
,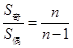 (其中
(其中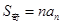 ,
,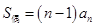 ).
).
17、如果一个数列从第 项起,每一项与它的前一项的比等于同一个常数,则这个数列称为等比数列,这个常数称为等比数列的公比.
项起,每一项与它的前一项的比等于同一个常数,则这个数列称为等比数列,这个常数称为等比数列的公比.
18、在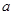 与
与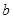 中间插入一个数
中间插入一个数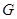 ,使
,使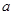 ,
,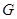 ,
,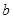 成等比数列,则
成等比数列,则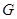 称为
称为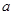 与
与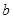 的等比中项.若
的等比中项.若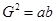 ,则称
,则称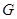 为
为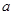 与
与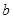 的等比中项.
的等比中项.
19、若等比数列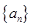 的首项是
的首项是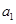 ,公比是
,公比是 ,则
,则 .
.
20、通项公式的变形:①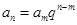 ;②
;② ;③
;③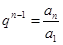 ;④
;④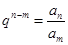 .
.
21、若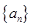 是等比数列,且
是等比数列,且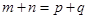 (
(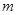 、
、 、
、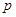 、
、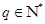 ),则
),则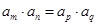 ;若
;若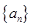 是等比数列,且
是等比数列,且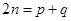 (
( 、
、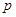 、
、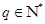 ),则
),则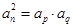 ;下角标成等差数列的项仍是等比数列;连续m项和构成的数列成等比数列。
;下角标成等差数列的项仍是等比数列;连续m项和构成的数列成等比数列。
22、等比数列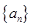 的前
的前 项和的公式:
项和的公式: .
.
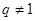 时,
时,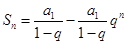 ,即常数项与
,即常数项与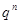 项系数互为相反数。
项系数互为相反数。
23、等比数列的前 项和的性质:①若项数为
项和的性质:①若项数为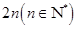 ,则
,则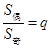 .
.
②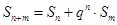 . ③
. ③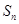 ,
,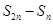 ,
,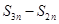 成等比数列.
成等比数列.
24、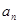 与
与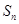 的关系:
的关系: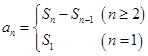
一些方法:
一、求通项公式的方法:
1、由数列的前几项求通项公式:待定系数法
①若相邻两项相减后为同一个常数设为 ,列两个方程求解;
,列两个方程求解;
②若相邻两项相减两次后为同一个常数设为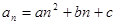 ,列三个方程求解;
,列三个方程求解;
③若相邻两项相减后相除后为同一个常数设为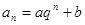 ,q为相除后的常数,列两个方程求解;
,q为相除后的常数,列两个方程求解;
2、由递推公式求通项公式:
①若化简后为 形式,可用等差数列的通项公式代入求解;
形式,可用等差数列的通项公式代入求解;
②若化简后为 形式,可用叠加法求解;
形式,可用叠加法求解;
③若化简后为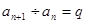 形式,可用等比数列的通项公式代入求解;
形式,可用等比数列的通项公式代入求解;
④若化简后为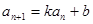 形式,则可化为
形式,则可化为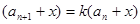 ,从而新数列
,从而新数列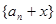 是等比数列,用等比数列求解
是等比数列,用等比数列求解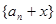 的通项公式,再反过来求原来那个。(其中
的通项公式,再反过来求原来那个。(其中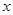 是用待定系数法来求得)
是用待定系数法来求得)
3、由求和公式求通项公式:
① ②
② 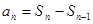 ③检验
③检验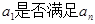 ,若满足则为
,若满足则为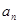 ,不满足用分段函数写。
,不满足用分段函数写。
4、其他
(1)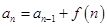 形式,
形式, 便于求和,方法:迭加;
便于求和,方法:迭加;
例如: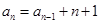
有: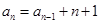
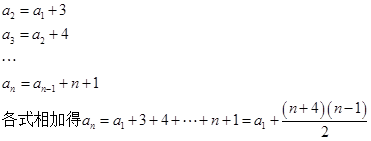
(2)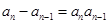 形式,同除以
形式,同除以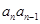 ,构造倒数为等差数列;
,构造倒数为等差数列;
例如: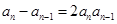 ,则
,则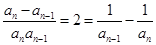 ,即
,即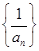 为以-2为公差的等差数列。
为以-2为公差的等差数列。
(3)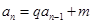 形式,
形式,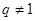 ,方法:构造:
,方法:构造: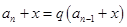 为等比数列;
为等比数列;
例如: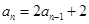 ,通过待定系数法求得:
,通过待定系数法求得: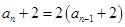 ,即
,即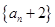 等比,公比为2。
等比,公比为2。
(4)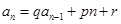 形式:构造:
形式:构造: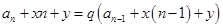 为等比数列;
为等比数列;
(5)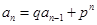 形式,同除
形式,同除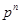 ,转化为上面的几种情况进行构造;
,转化为上面的几种情况进行构造;
因为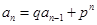 ,则
,则 ,若
,若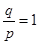 转化为(1)的方法,若不为1,转化为(3)的方法
转化为(1)的方法,若不为1,转化为(3)的方法
二、等差数列的求和最值问题:(二次函数的配方法;通项公式求临界项法)
①若 ,则
,则 有最大值,当n=k时取到的最大值k满足
有最大值,当n=k时取到的最大值k满足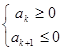
②若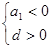 ,则
,则 有最小值,当n=k时取到的最大值k满足
有最小值,当n=k时取到的最大值k满足
三、数列求和的方法:
①叠加法:倒序相加,具备等差数列的相关特点的,倒序之后和为定值;
②错位相减法:适用于通项公式为等差的一次函数乘以等比的数列形式,如: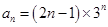 ;
;
③分式时拆项累加相约法:适用于分式形式的通项公式,把一项拆成两个或多个的差的形式。如: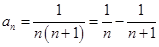 ,
,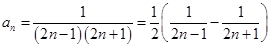 等;
等;
④一项内含有多部分的拆开分别求和法:适用于通项中能分成两个或几个可以方便求和的部分,如: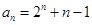 等;
等;
四、综合性问题中
①等差数列中一些在加法和乘法中设一些数为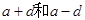 类型,这样可以相加约掉,相乘为平方差;
类型,这样可以相加约掉,相乘为平方差;
②等比数列中一些在加法和乘法中设一些数为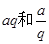 类型,这样可以相乘约掉。
类型,这样可以相乘约掉。
第三章:不等式
1、 ;
; ;
;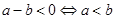 .
.
比较两个数的大小可以用相减法;相除法;平方法;开方法;倒数法等等。
2、不等式的性质: ①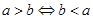 ;②
;②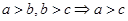 ;③
;③ ;
;
④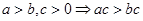 ,
,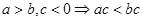 ;⑤
;⑤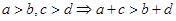 ;
;
⑥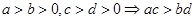 ;⑦
;⑦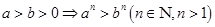 ;
;
⑧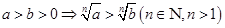 .
.
3、一元二次不等式:只含有一个未知数,并且未知数的最高次数是 的不等式.
的不等式.
4、二次函数的图象、一元二次方程的根、一元二次不等式的解集间的关系:

5、二元一次不等式:含有两个未知数,并且未知数的次数是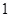 的不等式.
的不等式.
6、二元一次不等式组:由几个二元一次不等式组成的不等式组.
7、二元一次不等式(组)的解集:满足二元一次不等式组的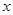 和
和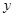 的取值构成有序数对
的取值构成有序数对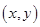 ,所有这样的有序数对
,所有这样的有序数对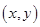 构成的集合.
构成的集合.
8、在平面直角坐标系中,已知直线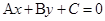 ,坐标平面内的点
,坐标平面内的点 .
.
①若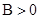 ,
, ,则点
,则点 在直线
在直线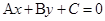 的上方.
的上方.
②若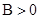 ,
,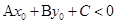 ,则点
,则点 在直线
在直线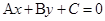 的下方.
的下方.
9、在平面直角坐标系中,已知直线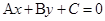 .
.
①若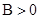 ,则
,则 表示直线
表示直线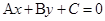 上方的区域;
上方的区域; 表示直线
表示直线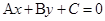 下方的区域.
下方的区域.
②若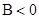 ,则
,则 表示直线
表示直线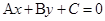 下方的区域;
下方的区域; 表示直线
表示直线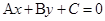 上方的区域.
上方的区域.
10、线性约束条件:由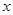 ,
,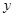 的不等式(或方程)组成的不等式组,是
的不等式(或方程)组成的不等式组,是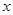 ,
,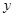 的线性约束条件.
的线性约束条件.
目标函数:欲达到最大值或最小值所涉及的变量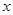 ,
,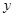 的解析式.
的解析式.
线性目标函数:目标函数为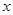 ,
,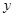 的一次解析式.
的一次解析式.
线性规划问题:求线性目标函数在线性约束条件下的最大值或最小值问题.
可行解:满足线性约束条件的解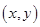 .
.
可行域:所有可行解组成的集合.
最优解:使目标函数取得最大值或最小值的可行解.
11、设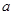 、
、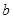 是两个正数,则
是两个正数,则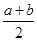 称为正数
称为正数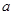 、
、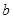 的算术平均数,
的算术平均数,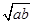 称为正数
称为正数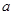 、
、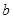 的几何平均数.
的几何平均数.
12、均值不等式定理: 若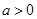 ,
,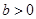 ,则
,则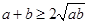 ,即
,即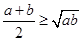 .
.
13、常用的基本不等式:
①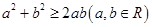 ;
;
②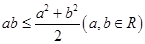 ;
;
③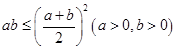 ;④
;④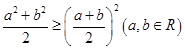 .
.
14、极值定理:设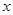 、
、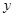 都为正数,则有
都为正数,则有
⑴若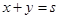 (和为定值),则当
(和为定值),则当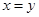 时,积
时,积 取得最大值
取得最大值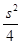 .
.
⑵若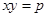 (积为定值),则当
(积为定值),则当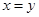 时,和
时,和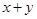 取得最小值
取得最小值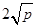 .
.
-
高一数学知识点归纳
集合与函数概念一集合有关概念1集合的含义某些指定的对象集在一起就成为一个集合其中每一个对象叫元素2集合的中元素的三个特性1元素的确…
-
人教版 高一数学知识点总结
高一数学知识总结必修一一集合一集合有关概念集合的含义集合的中元素的三个特性元素的确定性如世界上最高的山元素的互异性如由HAPPY的…
-
高一数学重要知识点总结
高一数学知识总结必修一一集合一集合有关概念1集合的含义2集合的中元素的三个特性1元素的确定性如世界上最高的山2元素的互异性如由HA…
-
高一数学必修一知识点总结
高一数学必修1各章知识点总结第一章集合与函数概念一、集合有关概念1.集合的含义2.集合的中元素的三个特性:(1)元素的确定性如:世…
-
高一数学集合知识点归纳及典型例题
一、、知识点:本周主要学习集合的初步知识,包括集合的有关概念、集合的表示、集合之间的关系及集合的运算等。在进行集合间的运算时要注意…
-
初中数学知识总结
高一物理综合练习题1、如图3-14所示,滑轮质量不计,三物处于平衡状态,设挂住定滑轮的绳子中的拉力大小为T,若把m2从右移到左边的…
-
PHP基础知识总结
$this的含义是表示实例化后的具体对象!我们一般是先声明一个类,然后用这个类去实例化对象!但是,当我们在声明这个类的时候,想在类…
-
电化学知识总结
一、原电池1、二次电池(铅蓄电池)负极:pb正极:PbO2电解质溶液:H2SO42?????正极pbo2(s)?so4(aq)?4…
-
电化学基础知识总结
第四章电化学基础知识总结第一节原电池原电池:1、概念:2、组成条件:①两个活泼性不同的电极②电解质溶液③电极用导线相连并插入电解液…
-
电化学原理知识总结
如果电极与参比电极之间的电压(电位差)测定值为+0.3V,则可以说这电极相对于参比电极的电位是+0.3V。参比电极以接地为基准,即…