数学分析知识点总结(微分方程)
2.7.微分方程初步
2.7.1概说
涉及到量的变化率满足的制约关系,通常是含有导数的方程——微分方程。
简单例子:
(1)放射性物质,在每一时刻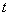 ,衰变的速率
,衰变的速率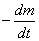 (由于是减少,因此
(由于是减少,因此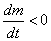 ,速率为标量,是正值)正比于该放射性物质尚存的质量,因此质量应满足一下微分方程。
,速率为标量,是正值)正比于该放射性物质尚存的质量,因此质量应满足一下微分方程。
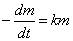
(2)质量为 的物体自由落体,取坐标轴沿竖直方向指向地心,下落距离
的物体自由落体,取坐标轴沿竖直方向指向地心,下落距离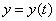 应该满足牛顿第二定律
应该满足牛顿第二定律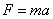 ,即
,即
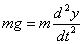
(3)质量为 的跳伞员下落,所受空气阻力正比下降的速度,取坐标轴沿竖直方向指向地心,则
的跳伞员下落,所受空气阻力正比下降的速度,取坐标轴沿竖直方向指向地心,则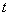 时刻下降距离
时刻下降距离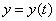 满足
满足
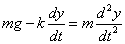
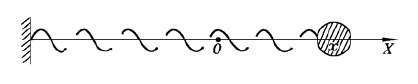
(1)如下图所示,钢球在以水平光滑杆上,受到弹力而来回整栋,原点位置为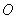 ,钢球在
,钢球在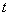 时刻的坐标
时刻的坐标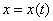 满足微分方程
满足微分方程
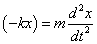
如果钢球还受到一个与速度成正比,方向与速度相反的阻尼力的作用,那么它所满足的微分方程是
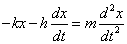
总结:最简单的一阶微分方程是
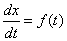
其中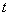 是自变量,上述方程的一般解应该是
是自变量,上述方程的一般解应该是
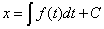
最简单的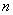 阶方程
阶方程
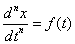
它等价于说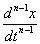 是
是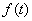 的原函数,即
的原函数,即
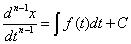
则再次积分,一直积分下去得到
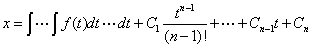
2.7.2一阶线性微分方程
考察下面的方程
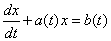
方程中有未知函数的一阶导数,且其一阶导数的系数为常数,其余部分未知函数最高层次数为一次,称为线性,上述方程为一阶线性微分方程。如果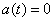 ,则称为一阶线性常微分方程。
,则称为一阶线性常微分方程。
试着求解上述方程,方程两端都乘以 ,得到
,得到

即为下面的形式
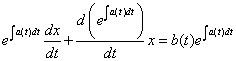
即
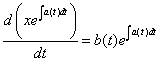
于是有
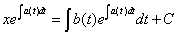
那么有
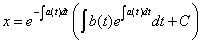
这就是一阶线性微分方程的一般解。这个解法的关键部分是以 乘以方程两端。
乘以方程两端。
简单的例子
(1)质量为 的跳伞员下落,所受空气阻力正比下降的速度,取坐标轴沿竖直方向指向地心,则
的跳伞员下落,所受空气阻力正比下降的速度,取坐标轴沿竖直方向指向地心,则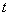 时刻下降距离
时刻下降距离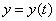 满足
满足
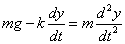
由于速度 ,因此方程化为
,因此方程化为
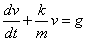
方程两边同时乘以 ,则有
,则有
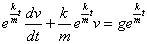
即有
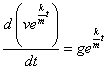
得到
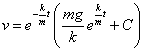
即
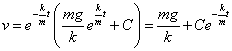
跳伞的初始速度为0,即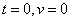 ,则
,则
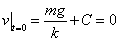
所以
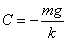
则跳伞速度为
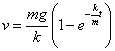
由于 ,因此有
,因此有

跳伞的初始位移为0,即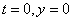 ,则
,则
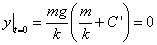
则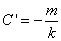
因此有

自然界有一些量,它的减少正比于该量本身数值,这样的量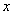 应该满足一下的微分方程
应该满足一下的微分方程
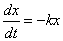
即
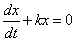
解这微分方程得到
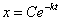
设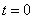 时
时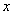 的值为
的值为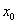 ,则有
,则有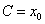 ,量
,量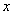 的变化规律为
的变化规律为
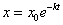
2.7.3变量分离型微分方程
先看一个简单的例子,考察一阶线性方程

我们把这个方程改写为
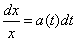
如果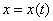 是方程的解,那么它能使上式成为恒等式,两边求不定积分得
是方程的解,那么它能使上式成为恒等式,两边求不定积分得
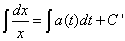
因此得到
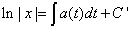
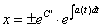
令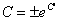 ,则得到
,则得到
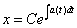
因此我们可以得到结论,方程

的一般解为
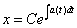
(一般的变量分离型方程)
对于一般的变量分离型方程
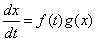
事实上,如果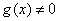 ,那么方程可以改写为
,那么方程可以改写为
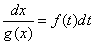
再对两边求不定积分得到

另外,如果有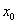 能使得
能使得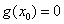 ,那么常值函数
,那么常值函数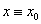 也是原方程的解。
也是原方程的解。
(经过换元后得到变量分离型方程)
(1)考察方程
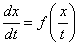
换元,引入新的未知数
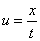
我们得到
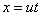
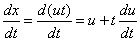
代入原方程得到
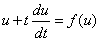
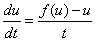
这又是一个变量分离型方程,我们有
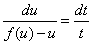
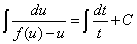
则有
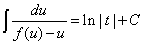
(2)考察方程
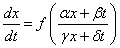
变换方程
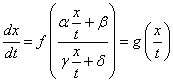
换元,令
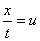
我们得到
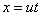
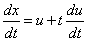
代入原方程,我们有
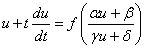
这是一个分离变量型的方程,得到
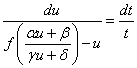
两边取积分得到
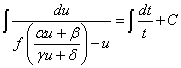
则得到

(3)考察方程

这个方程可以化成(2)中的形式,取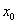 和
和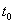 满足
满足
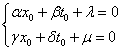
作如下变换
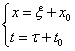
则有
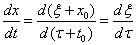
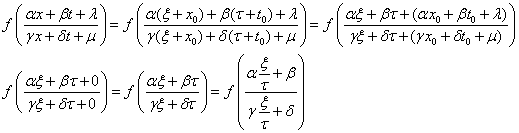
作换元,令
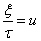
我们得到
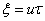
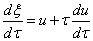
代入原方程,我们有
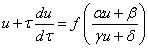
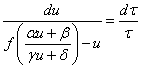
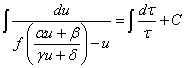
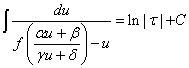
求解方程后只要将值还原为还原前的值。
2.7.4实变复值函数
对于代数方程式,我们已经有过这样的经验:即使是实系数的代数方程,为了弄清楚它的根的状况,最好到更广泛的复数范围内加以讨论。在处理微分方程的某些问题时,例如求解高阶常系数线性微分方程的时候也会遇到类似的问题:虽然是“实”的微分方程,所求的也是实解(实值函数解),但中间过程却需要在更广泛的复值函数范围内进行讨论。本节为这一讨论做准备。
(1)复数与平面向量,复数序列的极限
我们把形状如

的数称为复数,这里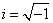 是虚单位,而
是虚单位,而 都是实数,分别称为实部和虚部,记为
都是实数,分别称为实部和虚部,记为
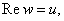
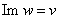
复数的加法和乘法定义如下:
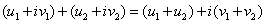
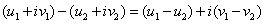
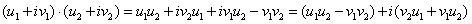
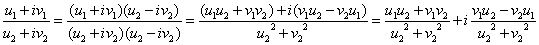
作除法时要求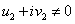 ,即
,即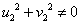 。
。
复数 可以解释为平面直角坐标系中坐标为
可以解释为平面直角坐标系中坐标为 的点,这点的极坐标为
的点,这点的极坐标为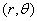 ,
,
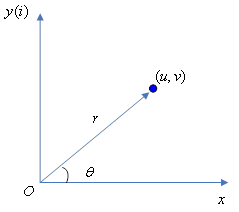
其中
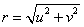 ,
,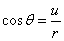 ,
,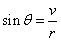
我们把
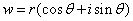
称为复数的极坐标表示,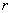 和
和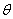 分别称为复数的模和幅角,分别用符号
分别称为复数的模和幅角,分别用符号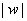 和
和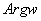 表示。采用这种表示来计算复数的乘方特别方便:
表示。采用这种表示来计算复数的乘方特别方便:
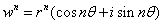
证明:
当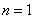 时明显成立,假设当
时明显成立,假设当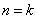 时成立,有
时成立,有
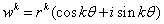
则当 时,有
时,有
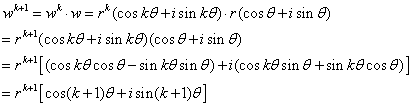
所以对 也成立,故而有
也成立,故而有
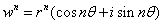
复数 还可以解释为长为
还可以解释为长为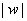 方位角为
方位角为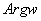 的一个平面向量,多个复数之和就可以理解为多个平面向量之和。复数的模正好是向量的长度,它满足一下不等式:
的一个平面向量,多个复数之和就可以理解为多个平面向量之和。复数的模正好是向量的长度,它满足一下不等式:
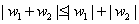
意味着三角形的两边之和大于第三边。也可以用代数方式证明这个不等式。化为代数表达,也就是证明:
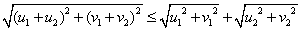
这个采用逆向证明法很容易证明,不等式还可以推广到 个复数的情形,则
个复数的情形,则
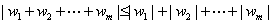
定理1:复数序列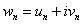 收敛于
收敛于 的充分必要条件是序列
的充分必要条件是序列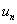 和序列
和序列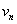 分别收敛于
分别收敛于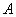 和
和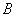 。
。
(实变复值函数)
设 ,
,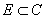 ,我们把从
,我们把从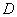 到
到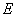 的映射
的映射
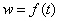
称为实变复值函数,设 ,
,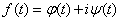 ,、函数
,、函数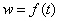 相当于一对实函数
相当于一对实函数
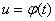 ,
,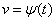
引入实变复值函数作为工具,是为了更方便地研究实函数。
定理1:设实变复值函数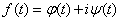 在
在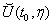 有定义,而
有定义,而 ,则
,则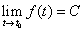 的充分必要条件是
的充分必要条件是
 ,
,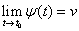
定理2:设实变复值函数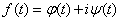 在
在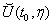 有定义,则
有定义,则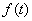 在
在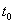 点连续的充分必要条件是:
点连续的充分必要条件是: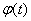 和
和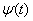 在
在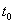 点连续。
点连续。
定理3:设实变复值函数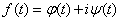 在
在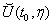 有定义,则
有定义,则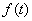 在
在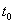 点可导的充分必要条件是:
点可导的充分必要条件是: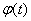 和
和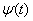 在
在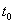 点可导。且
点可导。且

实函数的复合函数求导法则同样适用于实变复值函数的复合函数求导。
定理4:为使实变复值函数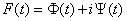 是实变复值函数
是实变复值函数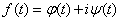 的原函数,必须而且只许
的原函数,必须而且只许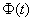 和
和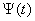 分别是
分别是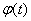 和
和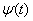 的原函数。记为
的原函数。记为
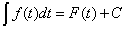
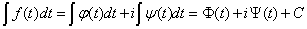
其中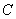 可以是复数。
可以是复数。
(欧拉Euler公式)
在推导过程中,会用到下面几个常见的极限
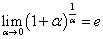 ,
,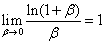 ,
,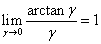
当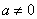 时,
时,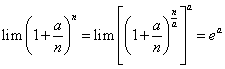 ;
;
当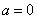 时,
时,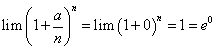 ;
;
因此有
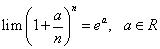
定义:对于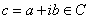 ,我们规定
,我们规定
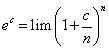
下面来求解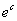 。
。
将复数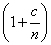 写成极坐标的形式
写成极坐标的形式
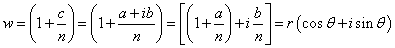
其中
 ,
,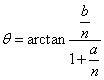
那么有
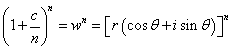
由前面的知识可得
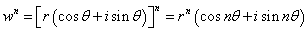
因此有
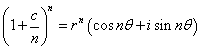
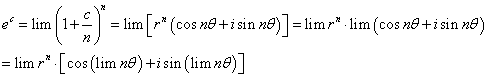
下面分别求出各部分的极限:
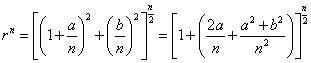
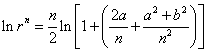
因此有(可用其同阶的无穷小替代)
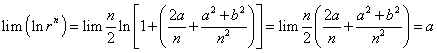
则有
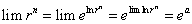
而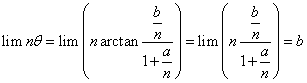
因此得到
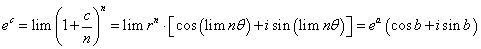
即
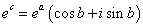 ,其中
,其中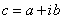
或者
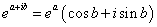
(1)如果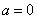 ,那么有
,那么有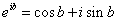
(2)令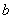 分别为
分别为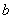 和
和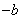 ,我们得到
,我们得到
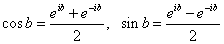
(3)推广到复数的指数运算

证:
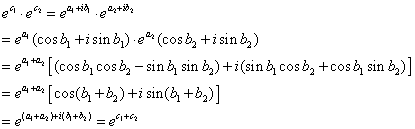
(4)令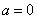 ,
,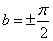 ,则得到
,则得到
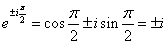
令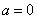 ,
,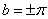 ,则得到
,则得到

令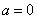 ,
,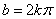 ,则得到
,则得到

特别的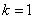 ,有
,有
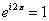
它将数学中最重要的五个数字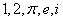 联系在一起。
联系在一起。
利用欧拉公式,我们将复数的极坐标形式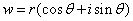 写成
写成

这里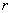 为复数的模,
为复数的模,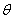 为幅角,
为幅角,
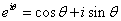
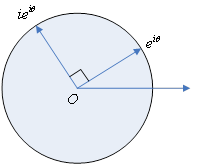
是一个模为1的复数,它表示与极轴夹角为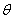 的一个单位向量。
的一个单位向量。
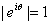
再看复数
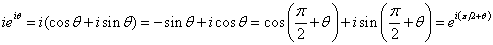
因为
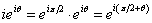
所以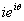 是与
是与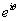 垂直的一个单位向量。如下图所示。
垂直的一个单位向量。如下图所示。
(应用欧拉公式讨论实变复值函数)
考察实变复值函数
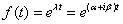 ,
,
这里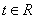 ,
,
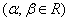 ,根据欧拉公式有
,根据欧拉公式有
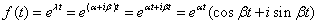
那么求导数得到
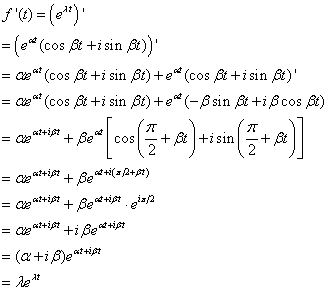
因此得到,对于 ,下面的求导公式也成立。
,下面的求导公式也成立。
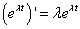
因此得到关于原函数不定积分的相应公式。
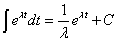
(1)例如,已知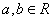 ,试求下面的不定积分。
,试求下面的不定积分。
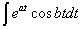 ,
,
令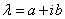 ,则所求的不定积分恰好为下式的实部和虚部
,则所求的不定积分恰好为下式的实部和虚部
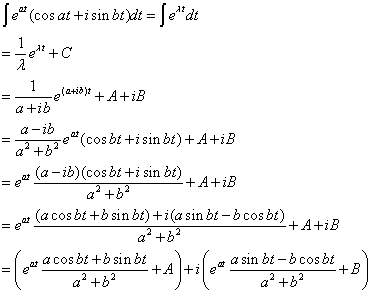
由于对于实变复值函数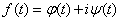
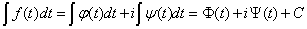
因此有
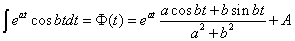
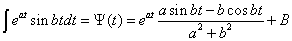
其中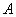 ,
,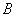 为任意实数。
为任意实数。
-
数学分析知识点
第一章1)洛必达法则求极限,最常用,要熟练;2)无穷小代换求极限,在解题中非常有用,几个等价公式要倒背如流;3)求含参数的极限,关…
-
数学分析知识点总结(微分方程)
27微分方程初步271概说涉及到量的变化率满足的制约关系通常是含有导数的方程微分方程简单例子1放射性物质在每一时刻t衰变的速率dm…
-
数学分析第三章知识点总结
4设f在ba上有定义limfx存在的充要条件是对任何含于ba且以xn为极限的数列xn极限limfxn都存在且相等limfx存在的充…
-
初中数学知识点归纳总结
初中数学知识点归纳总结一基本运算方法1配方法所谓配方就是把一个解析式利用恒等变形的方法把其中的某些项配成一个或几个多项式正整数次幂…
-
哈工大大一(下)工科数学分析期末考试知识点总结-刘星斯维提整理
11020xx班工科数学分析(下)知识点整理人:刘星斯维提(1):曲线积分:第一类曲线积分(对弧长的曲线积分):?x??(t)设f…
-
哈工大大一(下)工科数学分析期末考试知识点总结-刘星斯维提整理
11020xx班工科数学分析(下)知识点整理人:刘星斯维提(1):曲线积分:第一类曲线积分(对弧长的曲线积分):?x??(t)设f…
-
数学分析知识点
第一章1)洛必达法则求极限,最常用,要熟练;2)无穷小代换求极限,在解题中非常有用,几个等价公式要倒背如流;3)求含参数的极限,关…
-
初中数学圆的知识点总结
初中数学“圆”的知识点总结发布者:贺雪峰发布时间:20xx-11-814:41:421、圆是定点的距离等于定长的点的集合2、圆的内…
-
高中数学数列知识点总结(经典)
数列基础知识点和方法归纳1.等差数列的定义与性质定义:an?1?an?d(d为常数),an?a1??n?1?d等差中项:x,A,y…
-
小学数学知识点总结-人教版三年级下册
一、学习目标:1.使学生认识东、南、西、北四个方向,能够用给定的一个方向辨认其余的三个方向,并能用这些词语描述物体所在的方向;2.…
-
20xx年数学建模竞赛分析与总结
20xx年数学建模竞赛分析与总结20xx年我院组织三个队参加全国大学生数学建模竞赛,在学院教务处及基础部高度重视、关心和领导下,在…