空间向量_总结
第三章 空间向量 总结
空间向量定义及运算 直角坐标运算
概念: 向量
模 _________________________________________________
基线
零向量
相等向量
相反向量
共线向量 ________________________________________________
运算: 加法 ________________________________________________
减法 ________________________________________________
数乘向量 ________________________________________________
数量积 :定义 ________________________________________________
性质
运算律
基本定理:
共线
共面
空间分解
空间向量在立体几何中应用
概念: 直线的参数方程 平行:
垂直:
夹角:
距离:平面的向量表示式 方向向量 法向量 三垂线定理 三余弦定理 结论 线线平行 线面平行 面面平行 线线垂直 线面垂直 面面垂直 异面直线成角 线面成角 二面角 点面距离
异面直线 取值范围取值范围取值范围
第二篇:空间向量总结
空间向量的应用
一.基本概念
1.(1)用空间向量处理“平行”问题
设直线 的方向向量分别为
的方向向量分别为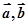 ,平面
,平面 的法向量分别为
的法向量分别为 ,则
,则
线线平行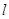 ∥
∥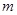

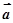 ∥
∥
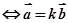 ; 线面平行
; 线面平行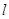 ∥
∥

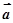

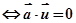 ;
;
面面平行 ∥
∥

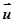 ∥
∥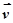

(2)用空间向量处理“垂直”问题
设直线 的方向向量分别为
的方向向量分别为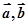 ,平面
,平面 的法向量分别为
的法向量分别为 ,则
,则
线线垂直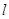 ⊥
⊥

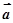 ∥
∥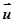
 ;
;
线面垂直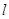 ⊥
⊥

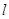 ⊥
⊥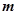 ,
,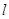 ⊥
⊥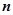 (
(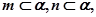
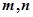 是两条相交的直线);
是两条相交的直线);
线面垂直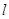 ⊥
⊥

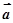 ∥
∥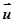
 ; 面面垂直
; 面面垂直  ⊥
⊥

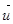 ⊥
⊥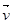
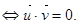
(3)设直线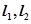 的方向向量分别为
的方向向量分别为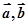 ,平面
,平面 的法向量分别为
的法向量分别为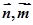 ,则
,则
异面直线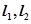 所成角:
所成角: 
直线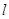 与平面
与平面 所成角:
所成角: 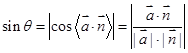
两个平面的夹角(平面 的法向量分别为
的法向量分别为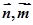 ):
):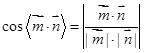
(4)异面直线间的距离的向量求法:已知异面直线l1、l2,AB为其公垂线段,C、D分别为l1、l2上的任意一点, 为与
为与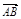 共线的向量,则|
共线的向量,则|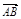 |=
|= .
.
(5)设平面α的一个法向量为 ,点P是平面α外一点,且Po∈α,则点P到平面α的距离是d=
,点P是平面α外一点,且Po∈α,则点P到平面α的距离是d=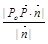 .
.
2.当解空间图形问题几何法难进行时,可以尝试运用空间向量(或坐标)来处理(三步曲):
(1)建立立体图形与空间向量的联系,用空间向量表示问题中涉及的点、直线、平面,把立体几何问题转化为向量问题(还常建立坐标系来辅助)(化为向量问题或向量的坐标问题)
(2)通过向量运算,研究点、直线、平面之间的位置关系及它们之间距离和夹角等问题(进行向量运算)
(3)把向量的运算结果“翻译”成相应的几何意义(回到图形)
第三篇:空间向量知识点整理
专题二空间向量
第一节 什么是空间向量
教学过程
(一)简单回顾平面向量
(二)引入空间向量,并准确理解空间向量
1.空间向量的一般运算
1)空间向量的概念:在空间,我们把具有大小和方向的量叫做向量
注:向量一般用有向线段表示;同向等长的有向线段表示同一或相等的向量
2)空间向量的运算
定义:与平面向量运算一样,空间向量的加法、减法与数乘向量运算如下:
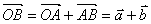 ;
; ;
;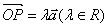
 运算律:⑴加法交换律:
运算律:⑴加法交换律: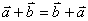
⑵加法结合律: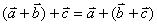
⑶数乘分配律:
⑷数乘结合律: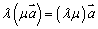
3)平行六面体:
平行四边形ABCD平移向量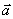 到
到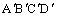 的轨迹所形成的几何体,叫做平行六面体,并记作:ABCD-
的轨迹所形成的几何体,叫做平行六面体,并记作:ABCD-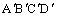 . 它的六个面都是平行四边形,每个面的边叫做平行六面体的棱.
. 它的六个面都是平行四边形,每个面的边叫做平行六面体的棱.
4)共线向量
如果表示空间向量的有向线段所在的直线互相平行或重合,则这些向量叫做共线向量或平行向量. 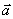 平行于
平行于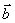 记作
记作 .
.
当我们说向量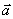 、
、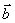 共线(或
共线(或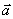 //
//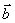 )时,表示
)时,表示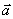 、
、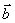 的有向线段所在的直线可能是同一直线,也可能是平行直线.
的有向线段所在的直线可能是同一直线,也可能是平行直线.
共线向量定理:空间任意两个向量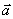 、
、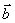 (
(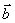 ≠
≠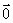 ),
),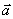 //
//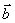 的充要条件是存在实数λ,使
的充要条件是存在实数λ,使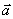 =λ
=λ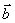 .
.
推论:如果 为经过已知点A且平行于已知非零向量
为经过已知点A且平行于已知非零向量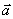 的直线,那么对于任意一点O,点P在直线
的直线,那么对于任意一点O,点P在直线 上的充要条件是存在实数t满足等式
上的充要条件是存在实数t满足等式

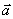 ……①.其中向量
……①.其中向量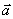 叫做直线
叫做直线 的方向向量.
的方向向量.
在 上取
上取 ,则①式可转化为
,则①式可转化为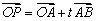 ……②,①②两式都称为空间直线的向量表示式.
……②,①②两式都称为空间直线的向量表示式.
5)共面向量
向量与平面平行:已知平面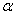 和向量
和向量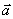 ,作
,作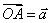 ,如果直线
,如果直线 平行于
平行于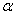 或在
或在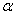 内,那么我们说向量
内,那么我们说向量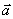 平行于平面
平行于平面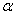 ,记作:
,记作: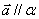 .通常我们把平行于同一平面的向量,叫做共面向量.
.通常我们把平行于同一平面的向量,叫做共面向量.
说明:空间任意的两向量都是共面的.
共面向量定理:如果两个向量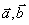 不共线,
不共线,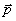 与向量
与向量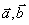 共面的充要条件是存在惟一实数
共面的充要条件是存在惟一实数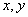 使
使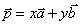 .
.
推论:空间一点 位于平面
位于平面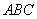 内的充分必要条件是存在有序实数对
内的充分必要条件是存在有序实数对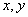 ,使
,使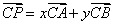 ……① 或对空间任一点
……① 或对空间任一点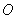 ,有
,有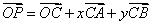 ……②
……②
或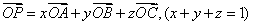 ……③
……③
上面①式叫做平面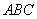 的向量表达式.
的向量表达式.
6)空间向量基本定理:如果三个向量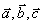 不共面,那么对空间任一向量
不共面,那么对空间任一向量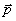 ,存在一个惟一的有序实数组
,存在一个惟一的有序实数组 ,使
,使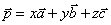 .
.
若三向量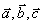 不共面,我们把
不共面,我们把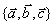 叫做空间的一个基底,
叫做空间的一个基底,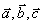 叫做基向量,空间任意三个不共面的向量都可以构成空间的一个基底.
叫做基向量,空间任意三个不共面的向量都可以构成空间的一个基底.
推论:设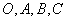 是不共面的四点,则对空间任一点
是不共面的四点,则对空间任一点 ,都存在唯一的三个有序实数
,都存在唯一的三个有序实数 ,使
,使

7)空间向量的夹角及其表示:已知两非零向量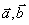 ,在空间任取一点
,在空间任取一点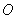 ,作
,作 ,则
,则 叫做向量
叫做向量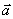 与
与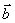 的夹角,记作
的夹角,记作 ;且规定
;且规定 ,显然有
,显然有 ;若
;若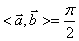 ,则称
,则称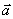 与
与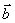 互相垂直,记作:
互相垂直,记作: .
.
8)向量的模:设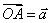 ,则有向线段
,则有向线段 的长度叫做向量
的长度叫做向量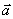 的长度或模,记作:
的长度或模,记作: .
.
9)向量的数量积:已知向量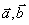 ,则
,则 叫做
叫做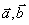 的数量积,记作
的数量积,记作 ,即
,即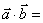
 .
.
 已知向量
已知向量 和轴
和轴 ,
, 是
是 上与
上与 同方向的单位向量,
同方向的单位向量,
作点 在
在 上的射影
上的射影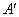 ,作点
,作点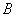 在
在 上的射影
上的射影 ,则
,则 叫做向量
叫做向量 在轴
在轴 上或在
上或在 上的正射影. 可以证明
上的正射影. 可以证明 的长度
的长度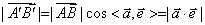 .
.
10)空间向量数量积的性质:
(1) .(2)
.(2) .(3)
.(3)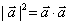 .
.
11)空间向量数量积运算律:
(1)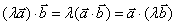 .(2)
.(2)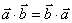 (交换律).
(交换律).
(3)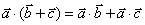 (分配律).
(分配律).
12)讲解范例:
 例1.已知线段
例1.已知线段 在平面
在平面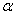 内,
内,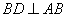 ,线段
,线段 ,若
,若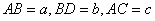 ,求
,求 间的距离.
间的距离.
例2.已知平行六面体 中,
中, ,
,

 ,求
,求 的长.
的长.
 例3.已知
例3.已知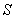 是边长为
是边长为 的正三角形所在平面外一点,且
的正三角形所在平面外一点,且 ,
,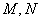 分别是
分别是 ,
,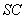 的中点,求异面直线
的中点,求异面直线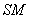 与
与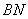 所成角的余弦值.
所成角的余弦值.
例4.如图,长方体 中,
中, ,
,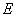 为
为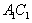 与
与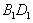 的交点,
的交点,
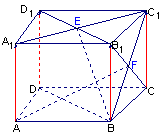
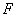 为
为 与
与 的交点,又
的交点,又 ,求长方体的高
,求长方体的高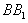 .
.
同步练习:
1.设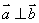 ,
, ,且
,且 ,求向量
,求向量 的模.
的模.
2.已知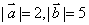 ,
, ,
, ,
, ,问实数
,问实数 取何值时
取何值时 与
与 垂直.
垂直.
3.若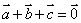 ,且
,且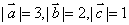 ,求
,求 的值.
的值.
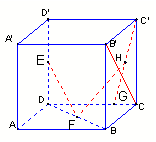 4.在棱长为1的正方体
4.在棱长为1的正方体 中,
中, 分别是
分别是 中点,
中点, 在棱
在棱 上,
上, ,
, 为
为 的中点,
的中点,
(1)求证: ;
;
(2)求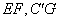 所成角的余弦;
所成角的余弦;
(3)求 的长
的长
2.空间向量的坐标运算
1)简单回顾空间直角坐标系的建立及点的坐标表示
2)(1)若 ,
, ,
,
则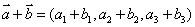 ,
,
 ,
, ,
,
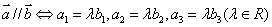 ,
,
(2)若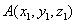 ,
, ,则
,则 .
.
一个向量在直角坐标系中的坐标等于表示这个向量的有向线段的终点的坐标减去起点的坐标.
(3)
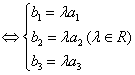
3)直线的方向向量及平面的法向量
(1)直线的方向向量:我们把直线 上的向量
上的向量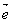 以及与
以及与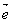 共线的向量叫做直线
共线的向量叫做直线 的方向向量
的方向向量
(2)平面的法向量:如果表示向量 的有向线段所在直线垂直于平面α,则称这个向量垂直于平面α,记作
的有向线段所在直线垂直于平面α,则称这个向量垂直于平面α,记作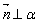 ,如果
,如果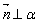 ,那么向量
,那么向量 叫做平面α的法向量.
叫做平面α的法向量.
注:①若 ,则称直线
,则称直线 为平面
为平面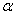 的法线;
的法线;
②平面的法向量就是法线的方向向量.
③给定平面的法向量及平面上一点的坐标,可以确定一个平面.
(3)在空间求平面的法向量的方法:
(i)直接法:找一条与平面垂直的直线,求该直线的方向向量.
(ii)待定系数法:建立空间直接坐标系
①设平面的法向量为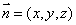
②在平面内找两个不共线的向量 和
和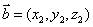
③建立方程组: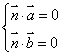
④解方程组,取其中的一组解即可.
第二节 利用空间向量解决立体几何问题
应用1:量的计算
1)计算角度大小
(1)求两异面直线所成的角
点 ,
, 直线
直线 ,
, ,
,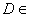 直线
直线 ,构成向量
,构成向量 ,
, ,
, . 设直线
. 设直线 与直线
与直线 所成的角为
所成的角为 ,则
,则 ,即
,即 或其补角为直线
或其补角为直线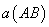 与
与 所成的角.
所成的角.
 例5. 如图,已知直棱柱ABC-A1B1C1,在
例5. 如图,已知直棱柱ABC-A1B1C1,在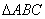 中,CA=CB=1,
中,CA=CB=1, ,棱AA1=2,求异面直线BA1,CB1所成的角.
,棱AA1=2,求异面直线BA1,CB1所成的角.
(2)求直线和平面所成的角
 已知
已知 ,
,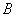 为直线
为直线 上任意两点,
上任意两点, 为平面
为平面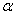 的法向量,则
的法向量,则 和平面
和平面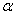 所成的角
所成的角 为:
为:
(1)当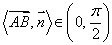 时,
时, ;
;
(2)当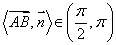 时,
时, .
.
例6. 棱长为a的正方体ABCD-A1B1C1D1中,E、F分别为C1D1、B1C1的中点,
 (1)求证:E、F、B、D共面;(略,不用做了)
(1)求证:E、F、B、D共面;(略,不用做了)
(2)求点A1D与平面EFBD所成的角的余弦值.
(3)求二面角
已知二面角 ,
,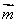 ,
, 分别为面
分别为面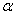 ,
, 的法向量,则二面角的平面角
的法向量,则二面角的平面角 的大小与两个法向量所成的角相等或互补. 即
的大小与两个法向量所成的角相等或互补. 即 或
或 .
.
注:如何判断二面角的平面角和法向量所成的角的关系?
①通过观察二面角锐角还是钝角,再由法向量的成的角求之.
②通过观察法向量的方向,判断法向量所成的角与二面角的平面角相等还是互补.

例7. 在四棱锥S-ABCD中∠DAB=∠ABC=90°,侧棱SA⊥底面AC,SA=AB=BC=1,AD=2,求二面角A-SD-C的余弦值的大小
2)计算空间距离
(1)求两条异面直线的距离
已知两条异面直线 ,
, ,
,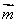 是与两直线都垂直的向量,
是与两直线都垂直的向量,  ,
, 则两条异面直线的距离
则两条异面直线的距离 .
.
 例8. 长方体ABCD-A1B1C1D1中AB=2,AD=4,AA1=6,E是BC的中点,F是CC1的中点,建立空间坐标系,求
例8. 长方体ABCD-A1B1C1D1中AB=2,AD=4,AA1=6,E是BC的中点,F是CC1的中点,建立空间坐标系,求
(1)异面直线D1F与B1E所成角的余弦值;
(2)二面角D1-AE-D的余弦值;
(3)异面直线B1E与D1F的距离.
(2)求点到面的距离(注:线到面和面到面的距离均可转化为点到面的距离进行求解)
 已知平面
已知平面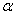 和点
和点 ,
,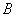 且
且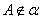 ,
, ,
, 为平面
为平面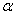 的法向量,则点
的法向量,则点 到平面
到平面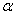 的距离
的距离 .
.
例9. 如图,在四棱锥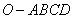 中,底面
中,底面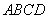 四边长为1的菱形,
四边长为1的菱形,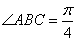 ,
,  底面
底面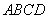 ,
,  ,
,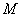 为
为 的中点,
的中点, 为
为 的中点.
的中点.
 (1)证明:直线
(1)证明:直线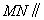 平面
平面 ;
;
(2)求异面直线 与
与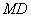 所成角的大小;
所成角的大小;
(3)求点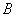 到平面
到平面 的距离.
的距离.
应用2:证明线与线、线与面和面与面的平行与垂直关系(略)
第三节 专题训练
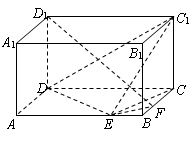 1.如右下图,在长方体ABCD-A1B1C1D1中,已知AB= 4, AD =3, AA1= 2.E、F分别是线段AB、BC上的点,且EB= FB=1.
1.如右下图,在长方体ABCD-A1B1C1D1中,已知AB= 4, AD =3, AA1= 2.E、F分别是线段AB、BC上的点,且EB= FB=1.
(1)求二面角C-DE-C1的正切值;
(2)求直线EC1与FD1所成的余弦值.
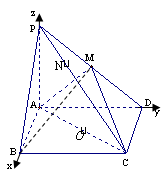
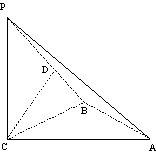 2.如图,三棱锥P—ABC中, PC
2.如图,三棱锥P—ABC中, PC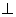 平面ABC,PC=AC=2,AB=BC,D是PB上一点,且CD
平面ABC,PC=AC=2,AB=BC,D是PB上一点,且CD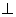 平面PAB.
平面PAB.
(1)求证:AB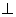 平面PCB;
平面PCB;
(2)求异面直线AP与BC所成角的大小;
(3)求二面角C-PA-B的大小的余弦值.
3.在四棱锥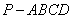 中,底面
中,底面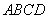 是矩形,
是矩形,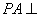 平面
平面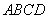 ,
,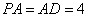 ,
,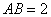 . 以
. 以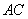 的中点
的中点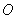 为球心、
为球心、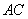 为直径的球面交
为直径的球面交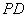 于点
于点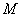 ,交
,交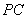 于点
于点 .
.
 (1)求证:平面
(1)求证:平面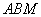 ⊥平面
⊥平面 ;
;
(2)求直线 与平面
与平面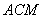 所成的角的大小;
所成的角的大小;
(3)求点 到平面
到平面 的距离.
的距离.
4.如图所示,已知在矩形ABCD中,AB=1,BC=a(a>0),PA⊥平面AC,且PA=1.
 (1)试建立适当的坐标系,并写出点P、B、D的坐标;
(1)试建立适当的坐标系,并写出点P、B、D的坐标;
(2)问当实数a在什么范围时,BC边上能存在点Q,
使得PQ⊥QD?
(3)当BC边上有且仅有一个点Q使得PQ⊥QD时,
求二面角Q-PD-A的大小.
5. 如题(19)图,在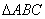 中,
中, ,
,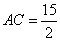 ,
,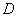 、
、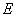 两点分别在
两点分别在 、
、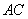 上. 使
上. 使 ,
, . 现将
. 现将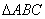 沿
沿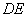 折成直二面角,求:
折成直二面角,求:
 (1)异面直线
(1)异面直线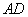 与
与 的距离;
的距离;
(2)二面角 的正切值.
的正切值.
-
空间向量知识点整理
专题二空间向量第一节什么是空间向量教学过程一简单回顾平面向量二引入空间向量并准确理解空间向量1空间向量的一般运算1空间向量的概念在…
-
空间向量基本知识点
高二理科空间向量补充编辑吴迪旭第十二讲空间向量基本理论知识梳理1空间向量的有关概念1空间向量空间里具有大小和方向的量叫做向量记为a…
-
空间向量知识点归纳总结
空间向量知识点归纳总结知识要点1空间向量的概念在空间我们把具有大小和方向的量叫做向量注12空间的两个向量可用同一平面内的两条有向线…
-
空间向量立体几何知识点集锦
空间向量立体几何知识点填空一空间向量的加法和减法点作ab则ab2求两个向量和的运算称为向量的加法在空间以同一点为起点的两个已知向量…
-
空间向量与立体几何知识点(改后)
1立体几何空间向量知识点总结一共面向量1定义平行于同一平面的向量叫做共面向量2共面向量定理若两个向量ab不共线则向量p与向量ab共…
-
向量总结
2.向量的概念(1)向量的基本概念①定义既有大小又有方向的量叫做向量。向量的大小也就是向量的长度,叫做向量的模。②特定大小或特定关…
-
排球赛总结
“辛格杯”排球赛总结20xx.12.8——20xx.12.17我系举行了第一届“辛格杯”排球比赛。通过这次比赛,不仅锻炼了我们的身…
-
艺术活动工作总结20xx.9
艺术活动工作总结圣井街道办第二小学20xx.9本学期我校的艺术工作在学校领导的关心支持下,按照学校对艺术工作的要求,以全面实施素质…
-
医生个人年终总结
目录医生个人年终总结.......................................................…
-
青年志愿者美化校园活动总结
青年志愿者活动是倡导团结友爱、助人为乐、见义勇为的社会风气,是当代中国社会主义一向十分高尚的事业。体现了中华民族助人为乐、扶贫济困…