第七章 矢量代数与空间解析几何

★类型（一）   向量的运算

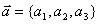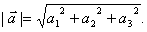解题策略  1. ，2.， 3. 利用

点积、叉积、混合积的性质及几何意义.

★类型（二）  求直线方程

解题策略  首先考虑直线方程的点向式与一般式，否则再用其它形式.

类型（三）  直线点向式与参数式转化

类型（四）  异面直线

★类型（五）  点到直线的距离、两直线的夹角

★类型（六）  求平面方程

解题策略  平面方程的点法式、一般式、平面束.

类型（七）  直线与平面的位置

类型（八）求曲线与曲面方程

解题对策  一般用定义求曲线与曲面方程

疑难问题点拨

 一般参数方程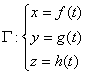绕Oz­轴旋转所成旋转曲面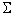的方程

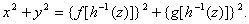
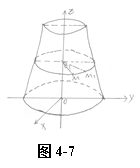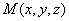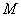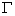证如图4-7， 设是曲面 上任意一点，而是由曲线上某点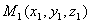（对应的参数为t₁）绕Oz轴旋转所得到。因此有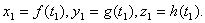

，

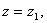
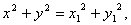
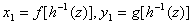故所求旋转曲面方程为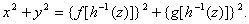

特别地，若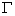绕Oz轴旋转时，且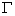参数方程表示为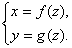则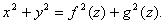

事实上，由前面的证明过程可知，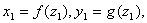

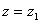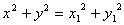
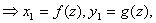     故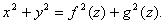

这个结果可作为一个规律记住，一个用参数方程表示的曲线绕某个坐标轴旋转所生成曲面的方程是：若把该曲线表示成该坐标轴对应的变量作为参数的参数方程，则旋转曲面的方程是由参数方程两个等式两边平方再相加得到等式。

第八章   多元函数的微分学

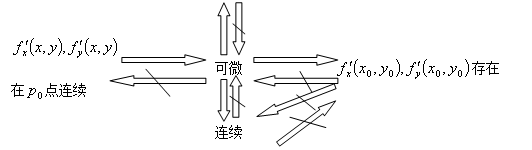在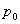点任意的方向导数都存在

注：这里“     ”表求推出，“      ”表示推不出，能推出的，都是定理，推不出的，我们在下面都举了反例。

类型1.1求多元函数的极限

解题策略1．利用初等多元函数的连续性，即若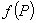是初等函数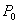，在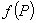的定义域中，则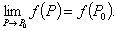

注：所谓的初等多元函数就是用一个数学表达式给出的解析式.

2．利用多元函数极限的四则运算。

3．转化为一元函数的极限，利用一元函数的极限来计算.

4．对于证明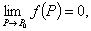或求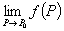时，感觉极限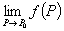可能时零，而直接又不容易证明或计算，这时可用夹逼定理，即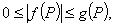而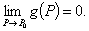

由夹逼定理知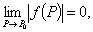从而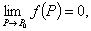

类型1.2判断多元函数的极限不存在

解题策略1．利用初等1．选取两条特殊的路径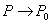，而函数值的极限存在，但不相等，则不存在。2.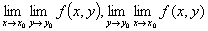 存在，但不相等

★类型1.3讨论多元函数的连续性

解题策略 用多元函数的连续定义

★类型1.4 求多元函数在一点的偏导数

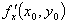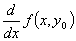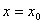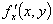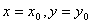解题策略 求有三种方法：（1）按定义；（2）求导函数，然后把代入；（3）求偏导函数，然后把代入。

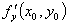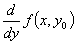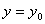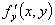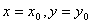求同样也有三种方法：（1）按定义；（2）求导函数，然后把；（3）求偏导函数，然后把代入。

类型1.5 判断多元函数在一点的可微性。

解题策略 1.偏导函数连续必可微.2.用可微定义

★类型1.6 求具体多元函数的偏导数

解题策略 本质上就是求一元函数的导数

★类型1.7 求多元复合函数的偏导数

解题策略 用多元复合函数求偏导公式。关键是搞清复合结构

★类型1.8 求多元隐函数的偏导数

解题策略 1.用多元隐函数求偏导公式.2. 用多元隐函数求偏导的方法.3.用全微分一阶不变性.

类型1.9 求多元隐函数组的偏导数

解题策略1. 用多元隐函数求偏导的方法.2.用全微分一阶不变性.

★类型1.10 求多元函数的方向导数与梯度

解题策略. 用方向导数的公式.2. 用方向导数的定义.3用梯度定义

★类型1.11 求多元函数的极值

解题策略. 求出驻点、偏导数不存在的点。对于出驻点，用取到极值的充分条件去判断；对于偏导数不存在的点永定义去判断。

类型1.12求多元函数的最值

解题策略. 建立二元函数，指出定义域，用最大值最小值定理.

★类型1.13 求多元函数的条件极值

解题策略 用拉格朗日乘数法.

★类型1.14曲面的切平面与曲线的切线（仅适合数学一）

解题策略 用曲面的切平面与曲线的切线的公式

第九章           多元函数积分学（二重积分）

★类型1.1二重积分在直角坐标下的计算

解题策略 画出积分区域，选择x-区域、y-区域

★类型1.2 求二重积分的累次积分

解题策略 根据累次积分的不等式画出积分区域，化成另一顺序的累次积分

★类型1.3 二重积分在极坐标下的计算

解题策略被积函数中有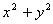或积分区域是圆域或圆域的一部分，用极坐标变换。

类型1.4 对称区域上的二重积分

解题策略 利用积分变量的地位对称性与被积函数关于积分变量的奇偶性简化计算.

类型1.5 计算二重广义积分

解题策略 画出积分区域，选择x-区域、y-区域或用极坐标变换

 

第二篇：微积分2方法总结

第七章 矢量代数与空间解析几何

★类型（一）   向量的运算

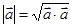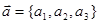解题策略  1. ，2.， 3. 利用

点积、叉积、混合积的性质及几何意义.

★类型（二）  求直线方程

解题策略  首先考虑直线方程的点向式与一般式，否则再用其它形式.

类型（三）  直线点向式与参数式转化

类型（四）  异面直线

★类型（五）  点到直线的距离、两直线的夹角

★类型（六）  求平面方程

解题策略  平面方程的点法式、一般式、平面束.

类型（七）  直线与平面的位置

类型（八）求曲线与曲面方程

解题对策  一般用定义求曲线与曲面方程

疑难问题点拨

 一般参数方程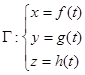绕Oz­轴旋转所成旋转曲面的方程

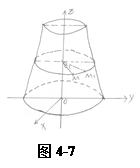证如图4-7， 设是曲面 上任意一点，而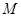是由曲线上某点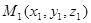（对应的参数为t₁）绕Oz轴旋转所得到。因此有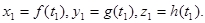

，

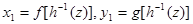故所求旋转曲面方程为

特别地，若绕Oz轴旋转时，且参数方程表示为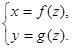则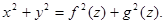

事实上，由前面的证明过程可知，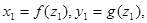

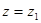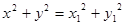
     故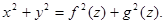

这个结果可作为一个规律记住，一个用参数方程表示的曲线绕某个坐标轴旋转所生成曲面的方程是：若把该曲线表示成该坐标轴对应的变量作为参数的参数方程，则旋转曲面的方程是由参数方程两个等式两边平方再相加得到等式。

第八章       多元函数的微分学

在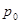点任意的方向导数都存在

注：这里“     ”表求推出，“      ”表示推不出，能推出的，都是定理，推不出的，我们在下面都举了反例。

类型1.1求多元函数的极限

解题策略1．利用初等多元函数的连续性，即若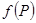是初等函数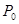，在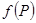的定义域中，则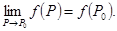

注：所谓的初等多元函数就是用一个数学表达式给出的解析式.

2．利用多元函数极限的四则运算。

3．转化为一元函数的极限，利用一元函数的极限来计算.

4．对于证明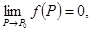或求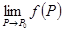时，感觉极限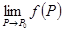可能时零，而直接又不容易证明或计算，这时可用夹逼定理，即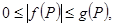而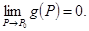

由夹逼定理知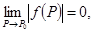从而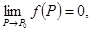

类型1.2判断多元函数的极限不存在

解题策略1．利用初等1．选取两条特殊的路径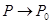，而函数值的极限存在，但不相等，则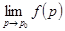不存在。2. 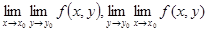存在，但不相等

★类型1.3讨论多元函数的连续性

解题策略 用多元函数的连续定义

★类型1.4 求多元函数在一点的偏导数

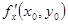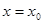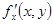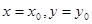解题策略 求有三种方法：（1）按定义；（2）求导函数，然后把代入；（3）求偏导函数，然后把代入。

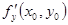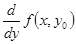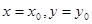求同样也有三种方法：（1）按定义；（2）求导函数，然后把；（3）求偏导函数，然后把代入。

类型1.5 判断多元函数在一点的可微性。

解题策略 1.偏导函数连续必可微.2.用可微定义

★类型1.6 求具体多元函数的偏导数

解题策略 本质上就是求一元函数的导数

★类型1.7 求多元复合函数的偏导数

解题策略 用多元复合函数求偏导公式。关键是搞清复合结构

★类型1.8 求多元隐函数的偏导数

解题策略 1.用多元隐函数求偏导公式.2. 用多元隐函数求偏导的方法.3.用全微分一阶不变性.

类型1.9 求多元隐函数组的偏导数

解题策略1. 用多元隐函数求偏导的方法.2.用全微分一阶不变性.

★类型1.10 求多元函数的方向导数与梯度

解题策略. 用方向导数的公式.2. 用方向导数的定义.3用梯度定义

★类型1.11 求多元函数的极值

解题策略. 求出驻点、偏导数不存在的点。对于出驻点，用取到极值的充分条件去判断；对于偏导数不存在的点永定义去判断。

类型1.12求多元函数的最值

解题策略. 建立二元函数，指出定义域，用最大值最小值定理.

★类型1.13 求多元函数的条件极值

解题策略 用拉格朗日乘数法.

★类型1.14曲面的切平面与曲线的切线（仅适合数学一）

解题策略 用曲面的切平面与曲线的切线的公式

第九章           多元函数积分学（二重积分）

★类型1.1二重积分在直角坐标下的计算

解题策略 画出积分区域，选择x-区域、y-区域

★类型1.2 求二重积分的累次积分

解题策略 根据累次积分的不等式画出积分区域，化成另一顺序的累次积分

★类型1.3 二重积分在极坐标下的计算

解题策略被积函数中有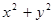或积分区域是圆域或圆域的一部分，用极坐标变换。

类型1.4 对称区域上的二重积分

解题策略 利用积分变量的地位对称性与被积函数关于积分变量的奇偶性简化计算.

类型1.5 计算二重广义积分

解题策略 画出积分区域，选择x-区域、y-区域或用极坐标变换