高一必修一基本初等函数知识点总结归纳
高一必修一函数知识点(12.1)
〖1.1〗指数函数
(1)根式的概念
①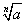 叫做根式,这里
叫做根式,这里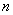 叫做根指数,
叫做根指数, 叫做被开方数.
叫做被开方数.
②当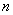 为奇数时,
为奇数时, 为任意实数;当
为任意实数;当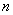 为偶数时,
为偶数时,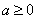 .
.
③根式的性质: ;当
;当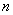 为奇数时,
为奇数时,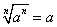 ;当
;当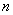 为偶数时,
为偶数时,  .
.
(2)分数指数幂的概念
①正数的正分数指数幂的意义是: 且
且 .0的正分数指数幂等于0.
.0的正分数指数幂等于0.
②正数的负分数指数幂的意义是: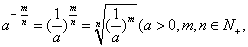 且
且 .0的负分数指数幂没有意义. 注意口诀:底数取倒数,指数取相反数.
.0的负分数指数幂没有意义. 注意口诀:底数取倒数,指数取相反数.
(3)分数指数幂的运算性质
① ②
② ③
③
(4)指数函数

例:比较
〖1.2〗对数函数
(1)对数的定义
①若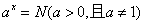 ,则
,则 叫做以
叫做以 为底
为底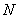 的对数,记作
的对数,记作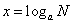 ,其中
,其中 叫做底数,
叫做底数,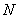 叫做真数.
叫做真数.
②对数式与指数式的互化: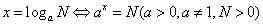 .
.
(2)常用对数与自然对数:常用对数: ,即
,即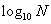 ;自然对数:
;自然对数: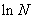 ,即
,即 (其中
(其中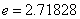 …).
…).
(3)几个重要的对数恒等式:  ,
, ,
, .
.
(4)对数的运算性质 如果 ,那么
,那么
①加法: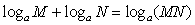 ②减法:
②减法:
③数乘: ④
④
⑤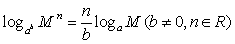 ⑥换底公式:
⑥换底公式:
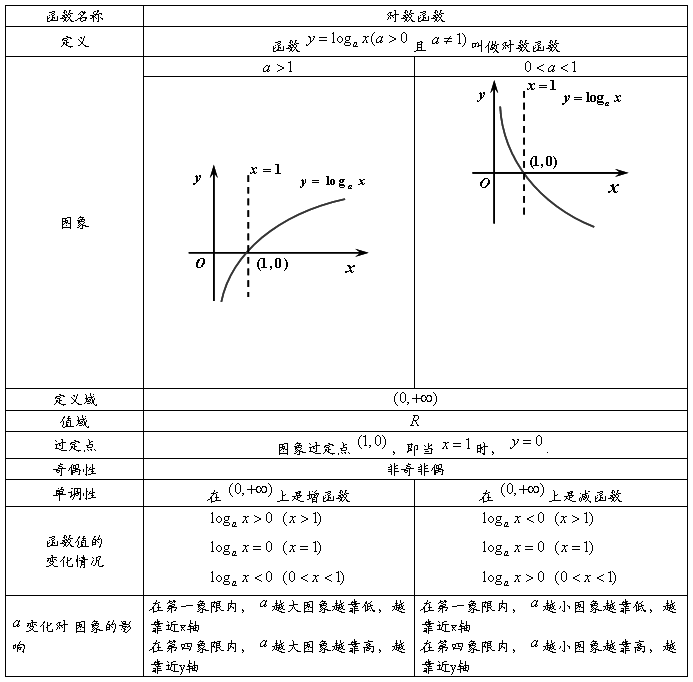
(5)对数函数
(6) 反函数的求法
①确定反函数的定义域,即原函数的值域;②从原函数式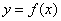 中反解出
中反解出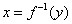 ;
;
③将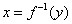 改写成
改写成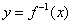 ,并注明反函数的定义域.
,并注明反函数的定义域.



 (7)反函数的性质
(7)反函数的性质
①原函数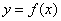 与反函数
与反函数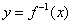 的图象关于直线
的图象关于直线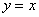 对称.
对称.
即,若 在原函数
在原函数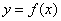 的图象上,则
的图象上,则 在反函数
在反函数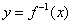 的图象上.
的图象上.
②函数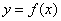 的定义域、值域分别是其反函数
的定义域、值域分别是其反函数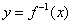 的值域、定义域.
的值域、定义域.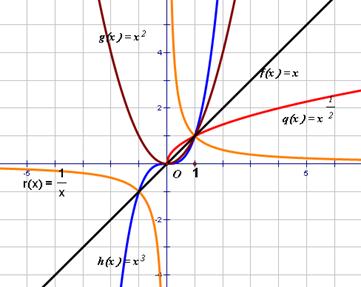
〖1.3〗幂函数
(1)幂函数的图象(需要知道x= ,1,2,3与y=
,1,2,3与y= 的图像)
的图像)
(2)幂函数的性质
①图象分布:幂函数图象分布在第一、二、三象限,第四象限无图象.
②过定点:图象都通过点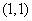 .
.
〖1.4〗二次函数
(1)二次函数解析式的三种形式
①一般式:
②顶点式:
③两根式:
(2)求二次函数解析式的方法
①已知三个点坐标时,宜用一般式.
②已知抛物线的顶点坐标或与对称轴有关或与最大(小)值有关时,常使用顶点式.
③若已知抛物线与 轴有两个交点,且横线坐标已知时,选用两根式求
轴有两个交点,且横线坐标已知时,选用两根式求 更方便.
更方便.
(3)二次函数图象的性质
①二次函数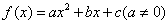 的图象是一条抛物线,对称轴方程为 ,顶点坐标是 。
的图象是一条抛物线,对称轴方程为 ,顶点坐标是 。
②在二次函数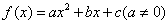 中
中
当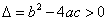 时,图象与
时,图象与 轴有 个交点.
轴有 个交点.
当 时,图象与 轴有1个交点.
轴有1个交点.
当 时,图象与 轴有没有交点.
轴有没有交点.
③当 时,抛物线开口向上,函数在 上递减,在
上递减,在 上递增,当
上递增,当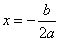 时,f(x)min= ;
时,f(x)min= ;
当 时,抛物线开口向下,函数在 上递增,在
上递增,在 上递减,当
上递减,当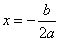 时,f(x)max= .
时,f(x)max= .
(4)一元二次方程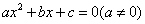 根的分布
根的分布
一元二次方程根的分布是二次函数中的重要内容,这部分知识在初中代数中虽有所涉及,但尚不够系统和完整,且解决的方法偏重于二次方程根的判别式和根与系数关系定理(韦达定理)的运用,下面结合二次函数图象的性质,系统地来分析一元二次方程实根的分布.
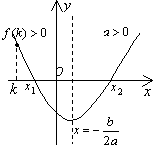
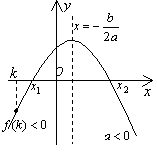
设一元二次方程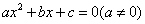 的两实根为
的两实根为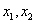 ,且
,且 .令
.令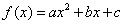 ,从以下四个方面来分析此类问题:①开口方向:
,从以下四个方面来分析此类问题:①开口方向: ②对称轴位置:
②对称轴位置: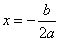 ③判别式:
③判别式: ④端点函数值符号.
④端点函数值符号.
①k<x1≤x2 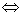
②x1≤x2<k 

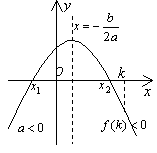
③x1<k<x2 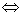 af(k)<0
af(k)<0
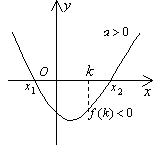

④k1<x1≤x2<k2 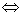

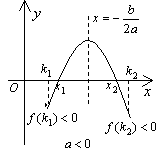
⑤有且仅有一个根x1(或x2)满足k1<x1(或x2)<k2  f(k1)f(k2)
f(k1)f(k2) 0,并同时考虑f(k1)=0或f(k2)=0这两种情况是否也符合
0,并同时考虑f(k1)=0或f(k2)=0这两种情况是否也符合
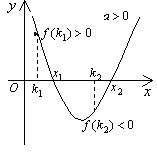
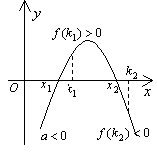
⑥k1<x1<k2≤p1<x2<p2 
此结论可直接由⑤推出.
第二篇:第二章_基本初等函数知识点总结
第二章 基本初等函数
一、指数函数
(一)指数与指数幂的运算
1.根式的概念:一般地,如果x?a,那么x叫做a的n次方根,其中n>1,且n∈N*.
? 负数没有偶次方根;0的任何次方根都是0,记作0?0。 当n是奇数时,an?a,当n是偶数时,an?|a|??2.分数指数幂
正数的分数指数幂的意义,规定:
n
?a(a?0)
?a(a?0)?
a?am(a?0,m,n?N*,n?1)a
?m
n
mn
,
?
1a
r
mn
?
1
am
(a?0,m,n?N*,n?1)
? 0的正分数指数幂等于0,0的负分数指数幂没有意义 3.实数指数幂的运算性质 (1)a〃a?a
r
r?s
(a?0,r,s?R);
rsrs
(a)?a(2) (a?0,r,s?R);rrs
(ab)?aa(a?0,r,s?R). (3)
(二)指数函数及其性质
1、指数函数的概念:一般地,函数y?ax(a?0,且a?1)叫做指数函数,其中x是自变量,函数的定义域为R.
注意:指数函数的底数的取值范围,底数不能是负数、零和1. 2
x
(1)在[a,b]上,f(x)?a(a?0且a?1)值域是[f(a),f(b)]或[f(b),f(a)]; (2)若x?0,则f(x)?1;f(x)取遍所有正数当且仅当x?R; (3)对于指数函数f(x)?a(a?0且a?1),总有f(1)?a; 二、对数函数 (一)对数
1.对数的概念:一般地,如果a?N(a?0,a?1),那么数x叫做以.a为底..N
第 1 页 共 4 页
x
x
的对数,记作:x?logaN(a— 底数,N— 真数,logaN— 对数式) 说明:○1 注意底数的限制a?0,且a?1; 2 ax?N?logaN?x; ○
3 注意对数的书写格式. ○
两个重要对数:
1 常用对数:以10为底的对数lgN; ○
2 自然对数:以无理数e?2.71828?为底的对数的对数lnN. ○
? 指数式与对数式的互化
幂值 真数
(二)对数的运算性质
如果a?0,且a?1,M?0,N?0,那么: 1 loga(M〃N)?logaM+logaN; ○
M
?logaM-logaN; N
3 logaMn?nlogaM (n?R). ○
2 loga○
注意:换底公式
logab?
logcb
(a?0,且a?1;c?0,且c?1;b?0).
logca
1n
(2)logab?. logab;
mlogba
利用换底公式推导下面的结论 (1)logambn?
(二)对数函数
1、对数函数的概念:函数y?logax(a?0,且a?1)叫做对数函数,其中x是自变量,函数的定义域是(0,+∞).
注意:○1 对数函数的定义与指数函数类似,都是形式定义,注意辨别。如:
y?2log2x,y?log5x 都不是对数函数,而只能称其为对数型函数.
5
2 对数函数对底数的限制:(a?0,且a?1). ○
2第 2 页 共 4 页
(三)幂函数
1、幂函数定义:一般地,形如y?x?(a?R)的函数称为幂函数,其中?为常数. 2、幂函数性质归纳.
(1)所有的幂函数在(0,+∞)都有定义并且图象都过点(1,1); (2)??0
时,幂函数的图象通过原点,并且在区间[0,??)上是增函数.特别地,当??1时,幂函数的图象下凸;当0???1时,幂函数的图象上凸;
(3)??0时,幂函数的图象在区间(0,??)上是减函数.在第一象限内,当x从右边趋向原点时,图象在y轴右方无限地逼近y轴正半轴,当x趋于??时,图象在x轴上方无限地逼近x轴正半轴.
例题:
1. 已知a>0,a
0,函数y=a与y=loga(-x)的图象只能是 ( )
x
log27?2log52
2.计算: ①log32?②24?log23= ;255= ;
log2764
1
③0.064??(?7)0?[(?2)3]??16?0.75?0.01 =
1418
3.函数y=log1(2x-3x+1)的递减区间为
2
2
4.若函数f(x)?logax(0?a?1)在区间[a,
2a]上的最大值是最小值的3倍,则a=
f(x)?0的
5.已知f(x)?log1?x(a?0且a?1),(1)求f(x)的定义域(2)求使
a
1?x
x的取值范围
第 3 页 共 4 页
第三章 函数的应用
一、方程的根与函数的零点
1、函数零点的概念:对于函数y?f(x)(x?D),把使f(x)?0成立的实数x叫做函数y?f(x)(x?D)的零点。
2、函数零点的意义:函数y?f(x)的零点就是方程f(x)?0实数根,亦即函数
y?f(x)的图象与x轴交点的横坐标。
即:方程f(x)?0有实数根?函数y?f(x)的图象与x轴有交点?函数y?f(x)有零点.
3、函数零点的求法:
1 (代数法)求方程f(x)?0的实数根; ○
2 (几何法)对于不能用求根公式的方程,可以将它与函数y?○
系起来,并利用函数的性质找出零点. 4、二次函数的零点:
二次函数y?ax2?bx?c(a?0).
(1)△>0,方程ax?bx?c?0有两不等实根,二次函数的图象与x轴有两个交点,二次函数有两个零点.
(2)△=0,方程ax?bx?c?0有两相等实根,二次函数的图象与x轴有一个交点,二次函数有一个二重零点或二阶零点.
(3)△<0,方程ax?bx?c?0无实根,二次函数的图象与x轴无交点,二次函数无零点. 5.函数的模型
第 4 页 共 4 页
22
f(x)的图象联
2
-
高一数学必修1函数知识点总结
函数?映射定义:设A,B是两个非空的集合,如果按某一个确定的对应关系,使对于集合A中的任意一个元素x,?在集合B中都有唯一确定的元…
-
高一数学必修一函数知识点总结
二函数的有关概念1函数的概念设AB是非空的数集如果按照某个确定的对应关系f使对于集合A中的任意一个数x在集合B中都有唯一确定的数f…
-
高一数学必修一知识点总结
高一数学必修1各章知识点总结第一章集合与函数概念一集合有关概念1集合的含义2集合的中元素的三个特性1元素的确定性如世界上最高的山2…
-
高中高一数学必修1各章知识点总结
高中高一数学必修1各章知识点总结第一章集合与函数概念一集合有关概念1集合的含义某些指定的对象集在一起就成为一个集合其中每一个对象叫…
-
高中数学必修1集合与函数知识点总结
高中数学必修1知识点总结第一章集合与函数概念111集合的含义与表示1集合的概念集合中的元素具有确定性互异性和无序性2常用数集及其记…
-
高一数学必修1函数知识点总结
函数?映射定义:设A,B是两个非空的集合,如果按某一个确定的对应关系,使对于集合A中的任意一个元素x,?在集合B中都有唯一确定的元…
-
高一数学必修一知识点总结
高一数学必修1各章知识点总结第一章集合与函数概念一集合有关概念1集合的含义2集合的中元素的三个特性1元素的确定性如世界上最高的山2…
-
高一数学必修一函数知识点总结
二函数的有关概念1函数的概念设AB是非空的数集如果按照某个确定的对应关系f使对于集合A中的任意一个数x在集合B中都有唯一确定的数f…
-
高一必修一物理知识点总结
一质点的运动1直线运动1匀变速直线运动1速度VtVoat2位移sVotat2V平tVt2t3有用推论VtVo2as4平均速度V平s…
-
高中物理必修一知识点总结
物理必修一知识考点归纳时间间隔能展示运动的一个过程时刻只能显示运动的一个瞬间对一些关于时间间隔和时刻的表述能够正确理解如第4s末4…
-
高中数学函数公式知识点总结
高中数学函数知识点总结(1)高中函数公式的变量:因变量,自变量。在用图象表示变量之间的关系时,通常用水平方向的数轴上的点自变量,用…