高中数列知识点总结
数列知识点总结
第一部分 等差数列
一 定义式: 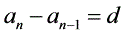
一个数列是等差数列的等价条件: (a,b为常数),即
(a,b为常数),即 是关于n的一次函数,因为
是关于n的一次函数,因为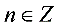 ,所以
,所以 关于n的图像是一次函数图像的分点表示形式。
关于n的图像是一次函数图像的分点表示形式。
二 通项公式: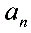
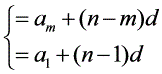
三 性质结论
1.3或4个数成等差数列求数值时应按对称性原则设置,如:3个数a-d,a,a+d; 4个数a-3d,a-d,a+d,a+3d
2. 与
与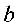 的等差中项
的等差中项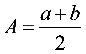 ;
;
在等差数列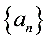 中,若
中,若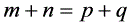 ,则
,则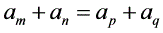 ;若
;若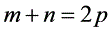 ,则
,则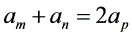 ;
;
3.若等差数列的项数为2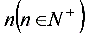 ,则
,则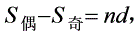
 ;
;
若等差数列的项数为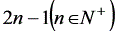 ,则
,则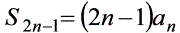 ,且
,且 ,
,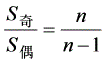
4.凡按一定规律和次序选出的一组一组的和仍然成等差数列。设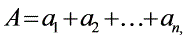
 ,
,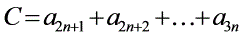 ,则有
,则有 ;
;
5. ,
, 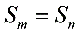 ,则前
,则前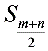 (m+n为偶数)或
(m+n为偶数)或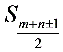 (m+n为奇数)最大
(m+n为奇数)最大
第二部分 等比数列
一 定义: 成等比数列。
成等比数列。
二 通项公式: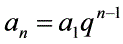 ,
,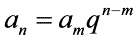
数列{an}是等比数列的一个等价条件是: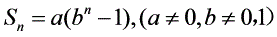 当
当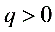 且
且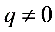 时,
时,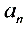 关于n的图像是指数函数图像的分点表示形式。
关于n的图像是指数函数图像的分点表示形式。
三 性质结论:
1.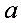 与
与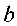 的等比中项
的等比中项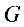
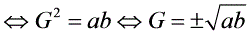 (
( 同号);
同号);
2.在等比数列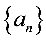 中,若
中,若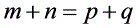 ,则
,则 ;若
;若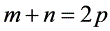 ,则
,则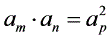 ;
;
3.设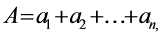 ,
,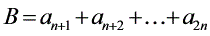 ,
,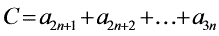 , 则有
, 则有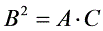
第三部分 求递推数列通项公式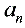
类型一:累加法 形如a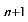 =a
=a + f (n), 其中f (n) 为关于n的多项式或指数形式(a
+ f (n), 其中f (n) 为关于n的多项式或指数形式(a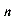 )或可裂项成差的分式形式.——可移项后叠加相消.
)或可裂项成差的分式形式.——可移项后叠加相消.
类型二: 累积法 形如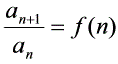 .其中f (n) =
.其中f (n) =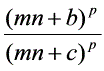 (p≠0,m≠0,b –c = km,k∈Z)或
(p≠0,m≠0,b –c = km,k∈Z)或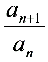 =kn(k≠0)或
=kn(k≠0)或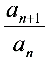 = km
= km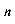 ( k ≠ 0, 0<m且m ≠ 1).
( k ≠ 0, 0<m且m ≠ 1).
类型三:形如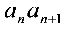 =
=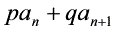 ,(pq ≠ 0).且
,(pq ≠ 0).且 的数列,——可通过倒数变形为基本数列问题.
的数列,——可通过倒数变形为基本数列问题.
当p = -q时,则有: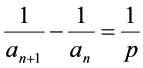 转化为等差数列;
转化为等差数列;
当p ≠ -q时,则有: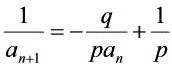 .同类型五转化为等比数列.
.同类型五转化为等比数列.
类型四:特征根法 形如a =pa
=pa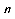 + q ,pq≠0 ,p、q为常数.
+ q ,pq≠0 ,p、q为常数.
当p =1时,为等差数列;
当p ≠1时,可在两边同时加上同一个数x,即a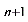 + x = pa
+ x = pa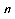 + q + x
+ q + x
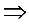 a
a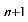 + x = p(a
+ x = p(a +
+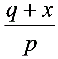 ), 令x =
), 令x =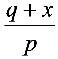 ∴x =
∴x =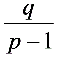 时,有a
时,有a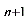 + x = p(a
+ x = p(a + x ),从而转化为等比数列 {a
+ x ),从而转化为等比数列 {a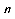 +
+ 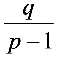 } 求解.
} 求解.
类型五:形如a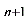 =pa
=pa + f (n),p≠0且 p为常数,f (n)为关于n的函数.
+ f (n),p≠0且 p为常数,f (n)为关于n的函数.
当p =1时,则 a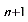 =a
=a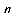 + f (n) 即类型一.
+ f (n) 即类型一.
当p ≠1时,f (n)为关于n的多项式或指数形式(a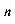 )或指数和多项式的混合形式.
)或指数和多项式的混合形式.
⑴若f (n)为关于n的多项式(f (n) = kn + b或kn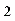 + bn + c,k、b、c为常数),——可用待定系数法转化为等比数列.
+ bn + c,k、b、c为常数),——可用待定系数法转化为等比数列.
⑵若f (n)为关于n的指数形式(a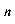 ).
).
①当p不等于底数a时,可转化为等比数列;
②当p等于底数a时,可转化为等差数列.
第四部分 求前n项和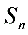
一:公式法求和直接用等差、等比数列的求和公式求和。
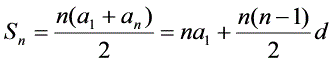
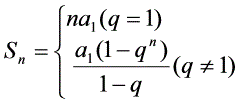 公比含字母时定要讨论
公比含字母时定要讨论
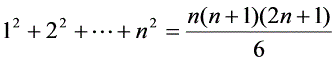

二.裂项相消法 这是分解与组合思想在数列求和中的具体应用. 裂项法的实质是将数列中的每项(通项)分解,然后重新组合,使之能消去一些项,最终达到求和的目的. 通项分解(裂项)如:
(1)1/n(n+1)=1/n-1/(n+1) (2)1/(2n-1)(2n+1)=1/2[1/(2n-1)-1/(2n+1)]
(3)1/n(n+1)(n+2)=1/2[1/n(n+1)-1/(n+1)(n+2)] (4)1/(√a+√b)=[1/(a-b)](√a-√b)
(5) n·n!=(n+1)!-n!(6)c/((n+a)(n+b))=(c/(a-b))*(1/( n+a)-1/(n+b))
小结:此类变形的特点是将原数列每一项拆为两项之后,其中中间的大部分项都互相抵消了。只剩下有限的几项。
注意: 余下的项具有如下的特点
1余下的项前后的位置前后是对称的。 2余下的项前后的正负性是相反的。
三.错位相减 如: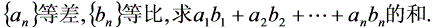
说明 求形如{an·bn}的数列的前n项和,若其中{an}成等差数列,{bn}成等比数列,则可采用推导等比数列求和公式的方法,即错位相减法,此方法体现了化归思想.
四:分组求和:把数列的每一项分成若干项,使其转化为等差或等比数列,再求和
五:合并求和:当通项公式中含有(-1)n,求和时可以对n的奇偶进行讨论,然后分情况求和.
例:1-2+3-4+5-6+……+(2n-1)-2n
可以先求出奇数项和偶数项的和,再相减。
但更好的方法是:(1-2)+(3-4)+(5-6)+……+[(2n-1)-2n]
8.其它求和法:如:归纳猜想法,奇偶法等
-
高中数列知识点总结归纳
一、等差数列1、等差数列定义:一般地,如果一个数列从第2项起,每一项与它的前一项的差等于同一个常数,那么这个数列就叫等差数列,这个…
-
高中数列知识点总结
数列第一部分等差数列一定义式:an?an?1?d二通项公式:an???am?(n?m)d??a1?(n?1)d一个数列是等差数列的…
-
高中数列知识点总结及经典习题解答
用心辅导中心高中数学数列知识点及经典习题二、重难点击一、本章重点:数列的概念,等差数列,等比数列的定义,通项公式和前n项和公式及运…
-
最新高中数列知识点总结
数列知识点总结第一部分等差数列一定义式:an?an?1?d二通项公式:an???am?(n?m)d?a?(n?1)d?1一个数列是…
-
高中数列知识点总结
第五章数列知识点总结第一部分数列S11.Sn?a1?a2?a3???an??ai2.an???i?1?Sn?Sn?1题型一归纳、猜…
-
高中数列知识点总结归纳
一、等差数列1、等差数列定义:一般地,如果一个数列从第2项起,每一项与它的前一项的差等于同一个常数,那么这个数列就叫等差数列,这个…
-
等差数列知识点总结
等差数列1.定义一般地,如果一个数列从第2项起,每一项与它的前一项的差等于同一个常数,那么这个数列就叫等差数列,这个常数叫做等差数…
-
等差数列知识点总结1111111111
等差数列1.定义一般地,如果一个数列从第2项起,每一项与它的前一项的差等于同一个常数,那么这个数列就叫等差数列,这个常数叫做等差数…
-
等差数列知识点总结
等差数列知识清单1、等差数列定义:一般地,如果一个数列从第2项起,每一项与它的前一项的差等于同一个常数,那么这个数列就叫等差数列,…
-
高中数学数列知识点总结
数列一、数列定义:数列是按照一定次序排列的一列数,是定义在正整数集N(或它的有限子集*{1,2,3,?,n})上的函数f(n),当…
-
高一物理必修一_人教版_知识点总结修改
补充:直线运动的图象1、从S—t图象中可求:⑴、任一时刻物体运动的位移⑵、物体运动速度的大小(直线或切线的斜率大小).......…