三角函数公式总结
三角函数公式总结
一、诱导公式
1. sin(180°+α)=-sinα, cos(180°+α)=-cosa
2. sin (α+k·360)=sin α, cos (α+k·360)=cos a, tan (α+k·360)=tan α
3. sin(-α)=-sina, cos(-a)=cosα
4*. tan(180°+α)=tanα, tan(-α)=-tanα
5. sin(180°-α)=sinα, cos(180°-α)=-cosα
6. sin(360°-α)=-sinα cos(360°-α)=cosα
7. sin(π/2-α)=cosα cos(π/2-α)=sinα
8*. Sin(3π/2-α)=-cosα cos(3π/2-α)=-sinα
9*. Sin(π/2+α)=cosα cos(π/2+a)=-sinα
10*.sin(3π/2+α)=-cosα cos(3π/2+α)=sinα
二、两角和与差的三角函数
1. 两点距离公式

2. S(α+β): sin(α+β)=sinαcosβ+cosαsinβ
C(α+β): cos(α+β)=cosαcosβ-sinαsinβ
3. S(α-β): sin(α-β)=sinαcosβ-cosαsinβ
C(α-β): cos(α-β)=cosαcosβ+sinαsinβ
4. T(α+β): 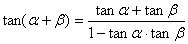
T(α-β): 
5*. 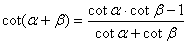
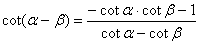
三、二倍角公式
1. S2α: sin2α=2sinαcosα
2. C2a: cos2α=cos2α-sin2a
3. T2α: tan2α=(2tanα)/(1-tan2α)
4. C2a’: cos2α=1-2sin2α cos2α=2cos2α-1
四*、其它杂项(全部不可直接用)
1.辅助角公式
asinα+bcosα=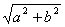 sin(a+φ),其中tanφ=b/a,其终边过点(a, b)
sin(a+φ),其中tanφ=b/a,其终边过点(a, b)
asinα+bcosα=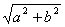 cos(a-φ),其中tanφ=a/b,其终边过点(b,a)
cos(a-φ),其中tanφ=a/b,其终边过点(b,a)
2.降次、配方公式
降次:
sin2θ=(1-cos2θ)/2 cos2θ=(1+cos2θ)/2
配方
1±sinθ=[sin(θ/2)±cos(θ/2)]2 1+cosθ=2cos2(θ/2) 1-cosθ=2sin2(θ/2)
3. 三倍角公式
sin3θ=3sinθ-4sin3θ cos3θ=4cos3-3cosθ
4. 万能公式
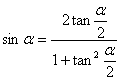
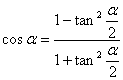
5. 和差化积公式
sinα+sinβ=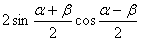
sinα-sinβ=
cosα+cosβ=
cosα-cosβ=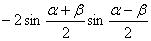
6. 积化和差公式
sinαsinβ=1/2[sin(α+β)+sin(α-β)]
cosαsinβ=1/2[sin(α+β)-sin(α-β)]
sinαsinβ-1/2[cos(α+β)-cos(α-β)]
cosαcosβ=1/2[cos(α+β)+cos(α-β)]
7. 半角公式
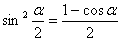


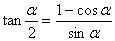
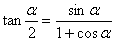
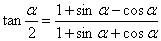
小计:57个
第二篇:三角函数公式总结
三角函数公式总结
一、三角函数基本知识
1. 几种终边在特殊位置时对应角的集合为

2.α、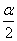 、2α之间的关系
、2α之间的关系
若α终边在第一象限则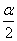 终边在第一或第三象限;2α终边在第一或第二象限或y轴正半轴。
终边在第一或第三象限;2α终边在第一或第二象限或y轴正半轴。
若α终边在第二象限则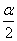 终边在第一或第三象限;2α终边在第三或第四象限或y轴负半轴。
终边在第一或第三象限;2α终边在第三或第四象限或y轴负半轴。
若α终边在第三象限则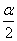 终边在第二或第四象限;2α终边在第一或第二象限或y轴正半轴。
终边在第二或第四象限;2α终边在第一或第二象限或y轴正半轴。
若α终边在第四象限则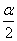 终边在第二或第四象限;2α终边在第三或第四象限或y轴负半轴。
终边在第二或第四象限;2α终边在第三或第四象限或y轴负半轴。
3. 三角函数基本关系式
(1)已知一点一角始边为x轴正半轴,终边上有一点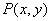 ,设
,设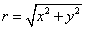 ,则
,则
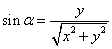 ,
, ,
,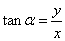
(2)同角三角函数关系式
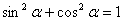
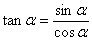
4. 诱导公式——“奇变偶不变,符号看象限”。
诱导公式一: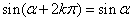 ,
,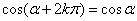 ,其中
,其中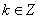

诱导公式二: 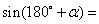
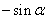 ;
; 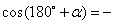
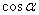
诱导公式三: 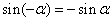 ;
; 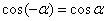
诱导公式四: ;
; 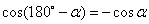

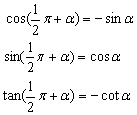 诱导公式五:
诱导公式五: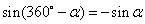 ;
; 
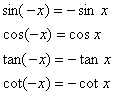

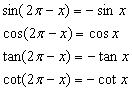
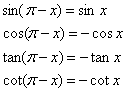
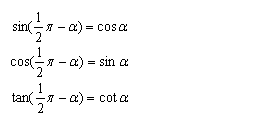
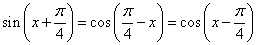 ;
;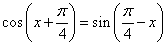 。
。
二、三角恒等变换
1. 和角与差角的三角函数
① 和角的余弦: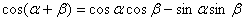
和角的正弦: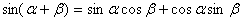
和角的正切: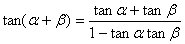
【变形1】 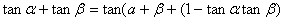
【变形2】 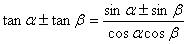
【变形3(正切分解)】 
② 差角的余弦: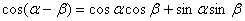
差角的正弦: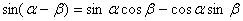
差角的正切:
【变形(正余弦平方差)】 

【和差角正余弦公式应用——辅助角公式】
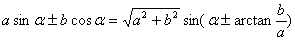
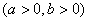
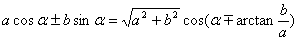
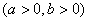
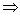 求值域常用:
求值域常用: 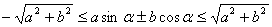
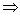 解答题常见变形:
解答题常见变形: 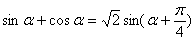
2. 倍半角公式
① 二倍角公式: 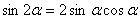
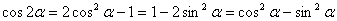
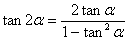
【推广公式】 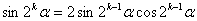
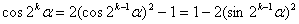
【常用变形】
降幂: 
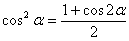
② 三倍角公式*: 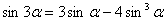
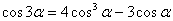
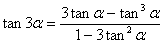
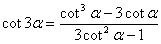
【变形(另一种形式的三倍角公式)】
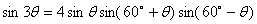

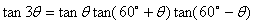
③ 半角公式: 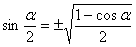

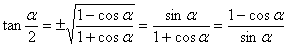 (±号的选择由角所在象限决定)
(±号的选择由角所在象限决定)
3. 三角恒等变换
① 万能公式
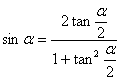
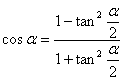
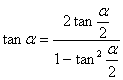
② 和差化积与积化和差
和差化积:

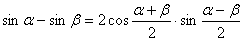

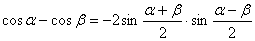
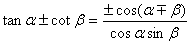
积化和差:
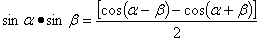

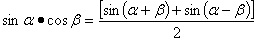

4. △ABC中,下列等式恒成立


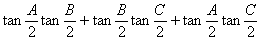
三、解三角形
1. 正弦定理
原始公式: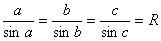 (R表示外接圆半径)
(R表示外接圆半径)
导出公式:
(1)三角形面积
导出:S=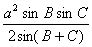 =
=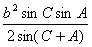 =
=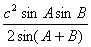 ;
;
S=2R2sinAsinBsinC。(R为外接圆半径)
(2)边角互化
① 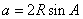 ,
,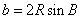 ,
,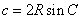
②  ,
,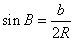 ,
,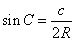
③  =
= =
=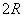
④ 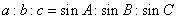
⑤ 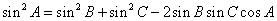
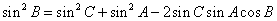

应用范围:① 已知一边与二角(a,B,C) 有解时有唯一解
② 已知两边和其中一边对角(a,b,A) 单解、双解、无解
2. 余弦定理
原始公式: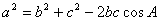
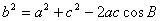

【导出公式】
(1) 边角关系(射影定理):
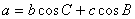
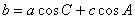
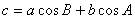
(2) 已知三边求余弦值:
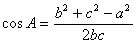

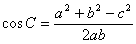
应用范围:① 已知两边与夹角(a,b,C) 有解时有唯一解
② 已知三边(a,b,c) 有解时有唯一解
3. 解三角形常用基本关系式
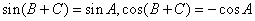
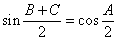
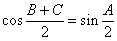
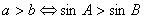
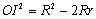 欧拉定理:
欧拉定理:
(其中O为△ABC外心,I为△ABC内心,R为外接圆半径,r为内接圆半径)
第三篇:三角函数公式总结
三角函数公式总结
一、诱导公式
1. sin(180°+α)=-sinα, cos(180°+α)=-cosa
2. sin (α+k·360)=sin α, cos (α+k·360)=cos a, tan (α+k·360)=tan α
3. sin(-α)=-sina, cos(-a)=cosα
4*. tan(180°+α)=tanα, tan(-α)=-tanα
5. sin(180°-α)=sinα, cos(180°-α)=-cosα
6. sin(360°-α)=-sinα cos(360°-α)=cosα
7. sin(π/2-α)=cosα cos(π/2-α)=sinα
8*. Sin(3π/2-α)=-cosα cos(3π/2-α)=-sinα
9*. Sin(π/2+α)=cosα cos(π/2+a)=-sinα
10*.sin(3π/2+α)=-cosα cos(3π/2+α)=sinα
二、两角和与差的三角函数
1. 两点距离公式

2. S(α+β): sin(α+β)=sinαcosβ+cosαsinβ
C(α+β): cos(α+β)=cosαcosβ-sinαsinβ
3. S(α-β): sin(α-β)=sinαcosβ-cosαsinβ
C(α-β): cos(α-β)=cosαcosβ+sinαsinβ
4. T(α+β): 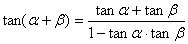
T(α-β): 
5*. 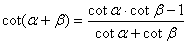
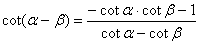
三、二倍角公式
1. S2α: sin2α=2sinαcosα
2. C2a: cos2α=cos2α-sin2a
3. T2α: tan2α=(2tanα)/(1-tan2α)
4. C2a’: cos2α=1-2sin2α cos2α=2cos2α-1
四*、其它杂项(全部不可直接用)
1.辅助角公式
asinα+bcosα=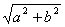 sin(a+φ),其中tanφ=b/a,其终边过点(a, b)
sin(a+φ),其中tanφ=b/a,其终边过点(a, b)
asinα+bcosα=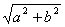 cos(a-φ),其中tanφ=a/b,其终边过点(b,a)
cos(a-φ),其中tanφ=a/b,其终边过点(b,a)
2.降次、配方公式
降次:
sin2θ=(1-cos2θ)/2 cos2θ=(1+cos2θ)/2
配方
1±sinθ=[sin(θ/2)±cos(θ/2)]2 1+cosθ=2cos2(θ/2) 1-cosθ=2sin2(θ/2)
3. 三倍角公式
sin3θ=3sinθ-4sin3θ cos3θ=4cos3-3cosθ
4. 万能公式
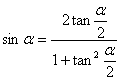
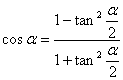
5. 和差化积公式
sinα+sinβ=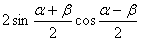
sinα-sinβ=
cosα+cosβ=
cosα-cosβ=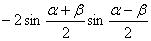
6. 积化和差公式
sinαsinβ=1/2[sin(α+β)+sin(α-β)]
cosαsinβ=1/2[sin(α+β)-sin(α-β)]
sinαsinβ-1/2[cos(α+β)-cos(α-β)]
cosαcosβ=1/2[cos(α+β)+cos(α-β)]
7. 半角公式
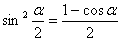


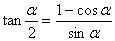
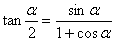
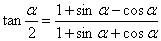
小计:57个
-
三角函数公式总结
一、诱导公式1.sin(180°+α)=-sinα,cos(180°+α)=-cosa2.sin(α+k·360)=sinα,co…
-
三角函数公式总结及其推倒
三角函数诱导公式:诱导公式记忆口诀:“奇变偶不变,符号看象限”。“奇、偶”指的是π/2的倍数的奇偶,“变与不变”指的是三角函数的名…
-
必修4 三角函数知识点归纳总结
必修4三角函数知识网络应用一任意角的概念与弧度制1将沿x轴正向的射线围绕原点旋转所形成的图形称作角逆时针旋转为正角顺时针旋转为负角…
-
三角函数公式大全--两页打印版
两角和公式sin(A?B)=sinAcosB?cosAsinBtan(A?B)?cos(A?B)=cosAcosB?sinAsin…
-
三角函数公式大全
三角函数公式大全sin30°=1/2sin45°=√2/2sin60°=√3/2cos30°=√3/2cos45°=√2/2cos…
-
三角函数公式总结
一、三角函数基本知识1.几种终边在特殊位置时对应角的集合为2.α、?、2α之间的关系2?终边在第一或第三象限;2α终边在第一或第二…
-
招商引资工作总结
工作总结1月x日,在某某区主任的带领下,、、等一行12人参加了在北京亮马河大厦举行的由海峡两岸经贸交流协会和某市人民政府共同举办的…
-
“四好”班子创建工作总结11.23
屏山县环境保护局二〇〇九年度“四好”班子创建工作总结20xx年我局在县委和县委组织部门的指导下,局领导班子及成员认真按照县委创“四…
-
区角活动的总结
区角活动总结在各项教学活动中,区角活动有着它的独特之处,它不仅深深地吸引每一位幼儿而且还使幼儿在其中得到发展。因此重视区角活动,合…
-
20xx年招商引资工作总结
20xx年乌兰县招商引资工作总结州经协办:现将乌兰县20xx年招商引资工作总结汇报如下,不妥之处,请批评指正。一、招商引资工作开展…