相似三角形总结(含答案)
相似三角形总结
一、如何证明三角形相似
例1、如图:点G在平行四边形ABCD的边DC的延长线上,AG交BC、BD于点E、F,则△AGD∽ ∽ 。

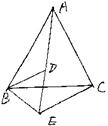


例2、已知△ABC中,AB=AC,∠A=36°,BD是角平分线,求证:△ABC∽△BCD
例3:已知,如图,D为△ABC内一点连结ED、AD,以BC为边在△ABC外作∠CBE=∠ABD,∠BCE=∠BAD
求证:△DBE∽△ABC
例4、矩形ABCD中,BC=3AB,E、F,是BC边的三等分点,连结AE、AF、AC,问图中是否存在非全等的相似三角形?请证明你的结论。
二、如何应用相似三角形证明比例式和乘积式
例5、△ABC中,在AC上截取AD,在CB延长线上截取BE,使AD=BE,求证:DF AC=BC
AC=BC FE
FE



例6:已知:如图,在△ABC中,∠BAC=900,M是BC的中点,DM⊥BC于点E,交BA的延长线于点D。
求证:(1)MA2=MD ME;(2)
ME;(2)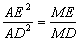
例7:如图△ABC中,AD为中线,CF为任一直线,CF交AD于E,交AB于F,求证:AE:ED=2AF:FB。
三、如何用相似三角形证明两角相等、两线平行和线段相等。



 例8:已知:如图E、F分别是正方形ABCD的边AB和AD上的点,且
例8:已知:如图E、F分别是正方形ABCD的边AB和AD上的点,且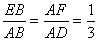 。求证:∠AEF=∠FBD
。求证:∠AEF=∠FBD

例9、在平行四边形ABCD内,AR、BR、CP、DP各为四角的平分线, 求证:SQ∥AB,RP∥BC
例10、已知A、C、E和B、F、D分别是∠O的两边上的点,且AB∥ED,BC∥FE,求证:AF∥CD
例11、直角三角形ABC中,∠ACB=90°,BCDE是正方形,AE交BC于F,FG∥AC交AB于G,求证:FC=FG
例12、Rt△ABC锐角C的平分线交AB于E,交斜边上的高AD于O,过O引BC的平行线交AB于F,求证:AE=BF
相似三角形总结(答案)
例1分析:关键在找“角相等”,除已知条件中已明确给出的以外,还应结合具体的图形,利用公共角、对顶角及由平行线产生的一系列相等的角。本例除公共角∠G外,由BC∥AD可得∠1=∠2,所以△AGD∽△EGC。再∠1=∠2(对顶角),由AB∥DG可得∠4=∠G,所以△EGC∽△EAB。
例2分析:证明相似三角形应先找相等的角,显然∠C是公共角,而另一组相等的角则可以通过计算来求得。借助于计算也是一种常用的方法。
证明:∵∠A=36°,△ABC是等腰三角形,∴∠ABC=∠C=72°又BD平分∠ABC,则∠DBC=36°
在△ABC和△BCD中,∠C为公共角,∠A=∠DBC=36°∴△ABC∽△BCD
例3分析: 由已知条件∠ABD=∠CBE,∠DBC公用。所以∠DBE=∠ABC,要证的△DBE和△ABC,有一对角相等,要证两个三角形相似,或者再找一对角相等,或者找夹这个角的两边对应成比例。从已知条件中可看到△CBE∽△ABD,这样既有相等的角,又有成比例的线段,问题就可以得到解决。
证明:在△CBE和△ABD中,∠CBE=∠ABD, ∠BCE=∠BAD∴△CBE∽△ABD∴ =
= 即:
即: =
=
△DBE和△ABC中,∠CBE=∠ABD, ∠DBC公用∴∠CBE+∠DBC=∠ABD+∠DBC∴∠DBE=∠ABC且 =
= ∴△DBE∽△ABC
∴△DBE∽△ABC
例4分析:本题要找出相似三角形,那么如何寻找相似三角形呢?下面我们来看一看相似三角形的几种基本图形:
(1) 如图:称为“平行线型”的相似三角形

(2)如图:其中∠1=∠2,则△ADE∽△ABC称为“相交线型”的相似三角形。

(3)如图:∠1=∠2,∠B=∠D,则△ADE∽△ABC,称为“旋转型”的相似三角形。
观察本题的图形,如果存在相似三角形只可能是“相交线型”的相似三角形,及△EAF与△ECA
解:设AB=a,则BE=EF=FC=3a,
由勾股定理可求得AE= , 在△EAF与△ECA中,∠AEF为公共角,且
, 在△EAF与△ECA中,∠AEF为公共角,且 所以△EAF∽△ECA
所以△EAF∽△ECA
 例5 分析:证明乘积式通常是将乘积式变形为比例式及DF:FE=BC:AC,再利用相似三角形或平行线性质进行证明:
例5 分析:证明乘积式通常是将乘积式变形为比例式及DF:FE=BC:AC,再利用相似三角形或平行线性质进行证明:
证明:过D点作DK∥AB,交BC于K,
∵DK∥AB,∴DF:FE=BK:BE
又∵AD=BE,∴DF:FE=BK:AD,而BK:AD=BC:AC
即DF:FE= BC:AC,∴DF AC=BC
AC=BC FE
FE
例6 证明:(1)∵∠BAC=900,M是BC的中点,∴MA=MC,∠1=∠C,
∵DM⊥BC,∴∠C=∠D=900-∠B,∴∠1=∠D,
∵∠2=∠2,∴△MAE∽△MDA,∴ ,∴MA2=MD
,∴MA2=MD ME,
ME,
(2)∵△MAE∽△MDA,∴ ,
, ∴
∴
评注:命题1 如图,如果∠1=∠2,那么△ABD∽△ACB,AB2=AD AC。
AC。
命题2 如图,如果AB2=AD AC,那么△ABD∽△ACB,∠1=∠2。
AC,那么△ABD∽△ACB,∠1=∠2。
例7 分析:图中没有现成的相似形,也不能直接得到任何比例式,于是可以考虑作平行线构造相似形。怎样作?观察要证明的结论,紧紧扣住结论中“AE:ED”的特征,作DG∥BA交CF于G,得△AEF∽△DEG, 。与结论
。与结论 相比较,显然问题转化为证
相比较,显然问题转化为证 。
。
证明:过D点作DG∥AB交FC于G则△AEF∽△DEG。(平行于三角形一边的直线截其它两边或两边的延长线所得三角形与原三角形相似)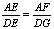 (1)
(1)
∵D为BC的中点,且DG∥BF∴G为FC的中点则DG为△CBF的中位线, (2)将(2)代入(1)得:
(2)将(2)代入(1)得:
例8 分析:要证角相等,一般来说可通过全等三角形、相似三角形,等边对等角等方法来实现,本题要证的两个角分别在两个三角形中,可考虑用相似三角形来证,但要证的两个角所在的三角形显然不可能相似(一个在直角三角形中,另一个在斜三角形中),所以证明本题的关键是构造相似三角形,
证明:作FG⊥BD,垂足为G。设AB=AD=3k则BE=AF=k,AE=DF=2k,BD=
∵∠ADB=450,∠FGD=900∴∠DFG=450∴DG=FG= ∴BG=
∴BG= ∴
∴
又∠A=∠FGB=900∴△AEF∽△GBF ∴∠AEF=∠FBD
例9 分析:要证明两线平行较多采用平行线的判定定理,但本例不具备这样的条件,故可考虑用比例线段去证明。利用比例线段证明平行线最关键的一点就是要明确目标,选择适当的比例线段。要证明SQ∥AB,只需证明AR:AS=BR:DS。
证明:在△ADS和△ARB中。
∵∠DAR=∠RAB= ∠DAB,∠DCP=∠PCB=
∠DAB,∠DCP=∠PCB= ∠ABC∴△ADS∽△ABR
∠ABC∴△ADS∽△ABR 
但△ADS≌△CBQ,∴DS=BQ,则 ,∴SQ∥AB,同理可证,RP∥BC
,∴SQ∥AB,同理可证,RP∥BC
例10分析:要证明AF∥CD,已知条件中有平行的条件,因而有好多的比例线段可供利用,这就要进行正确的选择。其实要证明AF∥CD,只要证明 即可,因此只要找出与这四条线段相关的比例式再稍加处理即可成功。
即可,因此只要找出与这四条线段相关的比例式再稍加处理即可成功。
证明:∵AB∥ED,BC∥FE∴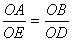 ,
,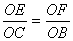 ∴两式相乘可得:
∴两式相乘可得:
例11 分析:要证明FC=FG,从图中可以看出它们所在的三角形显然不全等,但存在较多的平行线的条件,因而可用比例线段来证明。要证明FC=FG,首先要找出与FC、FG相关的比例线段,图中与FC、FG相关的比例式较多,则应选择与FC、FG都有联系的比作为过渡,最终必须得到 (“?”代表相同的线段或相等的线段),便可完成。
(“?”代表相同的线段或相等的线段),便可完成。
证明:∵ FG∥AC∥BE,∴△ABE∽△AGF 则有 而FC∥DE ∴△AED∽△AFC
而FC∥DE ∴△AED∽△AFC
则有 ∴
∴ 又∵BE=DE(正方形的边长相等)∴
又∵BE=DE(正方形的边长相等)∴ ,即GF=CF。
,即GF=CF。
例12 证明:∵CO平分∠C,∠2=∠3,故Rt△CAE∽Rt△CDO,∴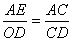
又OF∥BC,∴ 又∵Rt△ABD∽Rt△CAD,∴
又∵Rt△ABD∽Rt△CAD,∴ ,即
,即 ∴AE=BF。
∴AE=BF。
评注:应用比例线段证明两直线平行或两线段相等时,(1)要注意如果相关的比例式较多,一时难以作出选择,应将所有相关的比例式都写出来,然后再仔细对比、分析选出有用的。(2)要注意比例性质的灵活运用,善于总结比例式变换时的方法和技巧。变化时,要头脑清醒,思路清晰,一个字母也不放过,并且每一步都要有根有据,切不可无根据的乱变,或者相当然地硬变。
第二篇:排列组合总结(含答案)
1.(站队模型)4男3女站成一排:
①女生相邻;
②女生不相邻;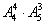
③女生从高到低排;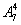
④甲不在排头,乙不在排尾;
解析:当甲在排尾时有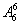 ;当甲不在排尾时有
;当甲不在排尾时有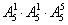
2.(组数模型)由0到9这10个数字组成没有重复数字的四位数:
①奇数;末位有
②偶数;
解析:末位为0,有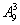 ;末位不为0,有
;末位不为0,有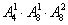
③被5整除的数;
解析:末位为0,有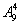 ;末位为5,有
;末位为5,有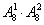
④比3257大的数;
解析:首位为4到9时有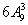 ;首位为3时
;首位为3时
⑤被3整除的三位数.

3.(分组分配问题)6个不同的小球:
①放入三个不同的盒子;
解析: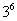
②放入三个不同的盒子,每盒不空;
解析:
③分三组(堆),每组至少一个;
解析:
4.6个相同的小球:
①放入三个不同的盒子;
解析:相当于分名额,盒子可空:插板法: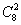
②放入三个不同的盒子,每盒不空;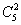
③恰有一个空盒.
解析:相当于两个盒子不空: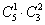
5.6名同学报名三科竞赛:
①每人限报一科;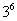
②每科限报一人;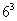
6.(选派问题)5男3女:
①选2人开会;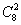
②选正副班长,至少1女;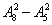
③选4人开会,至多2男;
解析:即至少2女,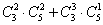
④选4人跑4×100接力,至少2女.
解析: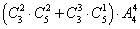
-
相似三角形总结(含答案)
相似三角形总结一、如何证明三角形相似例1、如图:点G在平行四边形ABCD的边DC的延长线上,AG交BC、BD于点E、F,则△AGD…
-
相似三角形知识点归纳(全)
相似三角形知识点归纳知识点1有关相似形的概念1形状相同的图形叫相似图形在相似多边形中最简单的是相似三角形2如果两个边数相同的多边形…
-
相似三角形知识点总结及习题
相似三角形基本知识(一)比例的性质1.比例的基本性质:比例式化积、积化比例式.ac??ad?bcbd2.合、分比性质:分子加(减)…
-
相似三角形 经典模型总结与例题分类
相似三角形经典模型总结经典模型精选例题平行型例1如图EE1FF1MM1若AEEFFMMB则SAEES四边形EEFFS四边形FFM1…
-
相似三角形复习总结
一知识点回顾三角形1三角形及有关概念1三角形两边之和大于第三边2三角形两边之差小于第三边三角形的角与角之间的关系1三角形三个内角的…
-
20xx年中医医院管理年活动总结
清水河县县中医院20xx年中医医院管理年活动工作总结根据国家中医药管理局《关于印发20xx年中医医院管理年活动方案的通知》文件要求…
-
四月份工作总结与计划
工作总结与计划人文社会科学学院20xx年x月x日学生工作:一、学生管理:1、进行专升本的统计工作;2、通知大三学生进行清考和补考的…
-
松河乡学前教育经济困难幼儿资助工作总结
松河乡关于落实学前教育家庭经济困难幼儿资助工作总结为贯彻落实贵州省财政厅、贵州省教育厅《省财政厅、教育厅关于下达20xx学前教育幼…
-
幼师毕业生实习总结报告
一个多月的实习生活,使我更深刻地了解到了一个幼儿教师的工作;更深刻地了解和掌握了中班这一年龄阶段的幼儿的身心发展特点及其在保教工作…
-
学前教育专业实习总结报告
姓名:朱凤云学号:205110380170实习单位:淮安市经济开发区徐杨乡徐杨小学幼儿园指导教师:刘老师实习时间:20xx年x月3…