概率公式整理

1．随机事件及其概率吸收律：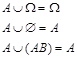  

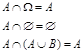
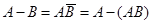
反演律：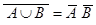               

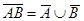
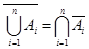
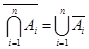
2．概率的定义及其计算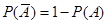：    若 

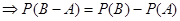
对任意两个事件A, B, 有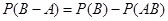   

加法公式：对任意两个事件A, B, 有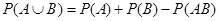      

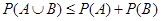
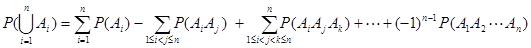
3．条件概率 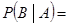 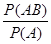  乘法公式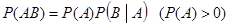

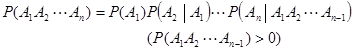
全概率公式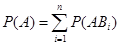 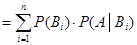Bayes公式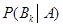 

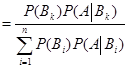
4．随机变量及其分布  分布函数计算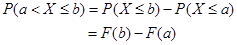

5．离散型随机变量  (1)  0 – 1 分布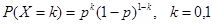

(2) 二项分布 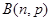若P ( A ) = p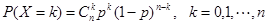

* Possion定理   有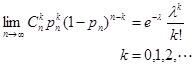 

(3)  Poisson 分布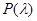    

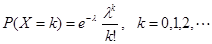
6．连续型随机变量 (1)   均匀分布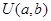 

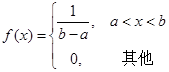
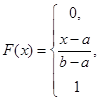
(2) 指数分布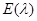       

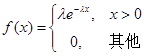
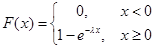
(3) 正态分布  N (m , s2 )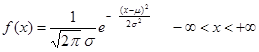     

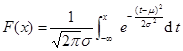
*N (0,1) — 标准正态分布            

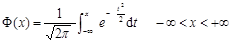
7.多维随机变量及其分布   二维随机变量( X ,Y )的分布函数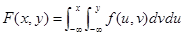  

边缘分布函数与边缘密度函数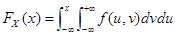   

  

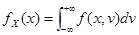
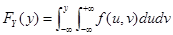
8. 连续型二维随机变量   (1)  区域G 上的均匀分布，U ( G )

(2) 二维正态分布

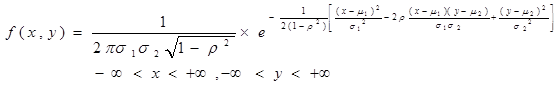
9. 二维随机变量的 条件分布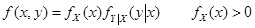  

   

          

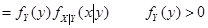
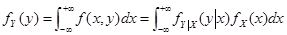
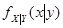
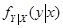
10. 随机变量的数字特征   数学期望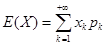 

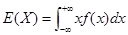
随机变量函数的数学期望 X 的 k 阶原点矩 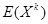  X 的 k 阶绝对原点矩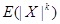 

X 的 k 阶中心矩 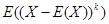   X 的 方差 

X ,Y 的 k + l 阶混合原点矩 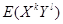    X ,Y 的 k + l 阶混合中心矩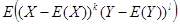 

X ,Y 的 二阶混合原点矩 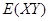   X ,Y 的二阶混合中心矩   X ,Y 的协方差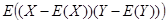

X ,Y 的相关系数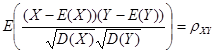    

X 的方差D (X ) = E ((X - E(X))2)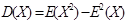

协方差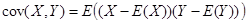

            

            

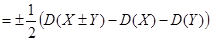
相关系数

 

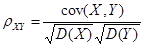
第二篇：概率论公式总结

?A???P?Bi?P?A|Bi?P 1.全概率公式：

i?1

n

P(Ai|B)?P(Ai)P(B｜Ai)2.贝叶斯公式：

?P(A)P(B｜A)

j

j

j?1

nk

n?k?k

?p?1?p??

n

3.二项分布：X~B(n,p) P{X?k}????E(X)=np D(x)=np(1-p)

4.泊松分布：X~π(λ) p(k?)E(x)= λ D(x)= λ

k?0,1,,n

?k??

P?(X?)

k!

e

, k=0,1,2,

5.泊松定理：随机变量X服从二项分布，又设nP=λ, 则有

n???

limCP(1?Pn)k

nn

n?k

=

?ke??

k!

6.均匀分布：

?1

,x??a,b??

，记作X~U?a,b? D(x)=(b-a)^2/12 f(x)??b?a

??0,else

7.指数分布：

?1?x,x?0,?e

f?x???θ

?其它,?0,

D(x)= θ ^2 E(x)= θ

128.正态分布： f (x)?

e2?, 记作：X~N(?,?2) D(X)= ?2 ???x??

?

(x??)2

TH1. 设XN(?,?2), YN(?,?2),且X,Y相互独立,1122

则 X?YN(???,?2??2)

1212

TH2. 设X1,X2,...,Xn相互独立,且XiN(?i,?i2)(i?1,2,

...,n),对于任意不全为0的常数C1,C2,...,Cn,有

22

U?C1X1?...?CnXnN(C1?1?...?Cn?n,C12?12?...?Cn?n)

?j?1?

9.边缘分布律： P?X?xi???P?X?xi,Y?yj???pij

j?1

?

P?Y?yj???

i?1

P?X?xi,Y?yj??

?

pijp.j?i?1

?

10.边缘概率密度： fX(x)????f(x,y)dy11.卷积公式：

???

?

fY(y)??f(x,y)dx

??

fZ(z)??fX(x)fY(z?x)dx

?

12.数学期望：离散型：E(X)=?xkpk E(Y)=

k?1

?Pg(x

k

k?1

?

k

)

??

连续型：E(X)=?xf(x)dx E(Y)=?g(x)f(x)dx

??

??

13.数学期望的性质：E (C ) = C E (aX ) = a E (X )

n

?n?

E (X + Y ) = E (X ) + E (Y ) E??aiXi?C???aiE(Xi)?C

?i?1?i?1

当X ,Y 独立时，E (X Y ) = E (X )E (Y )

14.方差：离散型：D(X)?E{[X?E(X)]}??[(xi?E(X)]2?pi

2

i?1?

?

2

连续型：D(X)??[(x?E(X)]f(x)dx

??

)]D(X) ? E ( X ) ? [ E ( X

22

D(X?Y)?D(X)?D(Y)

?2E{[X?E(X)][Y?E(Y)]}

E{[X-E(x)][Y-E(Y)]}=E(XY)-E(x)E(y) 15.方差性质：D (C) = 0 D (aX ) = a^2D(X) 16.

协

方

差

：

Cov(X,Y)=E{[X?E(X)][Y?E(Y)]}

Cov(a1X+b1,a2Y+b2)=a1a2Cov(X,Y) Cov(X1+X2,Y)=Cov(X1,Y)+Cov(X2,Y)

Cov(X,Y)

17.相关系数： ?XY?(n)分布：N为自由度，X^2=x1^2+x2^2……xn^2 18. ? 2

密度函数：

xn?11??ex,x?0?nf(x)??2?()

?

0,x?0?

?

2若X1??2(n1),X2??2(n2),X1,X2相互独立， 性质：可加性：

3?n??时，?2(n)?正态分布数学期望E=n，方差D=2n

X19.t分布： X~N(0,1),Y~?2(n),T?

则X1＋X2～?2(n1＋n2)

?n?1?n?1Γ??2?2

t??

概率密度： f(t)??2??????t??

Γ?1?

?n???n???2?

?t2

性质： n??,fn(t)??(t)?

1?2

e

20.F分布：X和Y都服从X分布 F=Xn2/Yn1 ???Γ??n?m??2?n??n??n?mn?1?n?2 概率密度： f(t,n,m)????t?1??Γ??n?mt?

t?0?2??Γ??m??m???

?2?

??

??0,t?0性质： 1若F~F(n,m),则1/F~F(m,n)21.正态总体均值检验：

(1) 方差? 2已知, ? 的置信区间 (X?z

?

?n

,X?z?

?

n

)???(1)

(2) 方差? 2未知 , ? 的置信区间??

? ?t?(n?1)Sn

,?t?

(n?1)S?n??

???(3) 方差? 2

的置信区间 ??(n?1)S2(n?1)S2

,?

?2???2?(n?1)?1??????(3)(n?1)?

方差已知

?1??2

的

置信区间为

???22221????

?(?)?z??

n?2,(?)?z1?21n2n1n2

??

方

差

未

知

?1

? ?2

的

置信区间为

??11(n221?1)S1?(n2?1)S2?

?(?)?t??

n?1n2n1?n2?2

??

方差比的置信区间为

??S2

?11

S2

11

????S2

2F(n?1,n,2?1)S2?

?12

F?

1?

?(n1?1,n2?1)?

22??

(2)