高中数学圆锥曲线总结
数学圆锥曲线总结
1、圆锥曲线的两个定义:
(1)第一定义中要重视“括号”内的限制条件:椭圆中,与两个定点F,F的距离的和等于常数,且此常数一定要大于,当常数等于时,轨迹是线段FF,当常数小于
距离的差的绝对值等于常数对值”与时,无轨迹;双曲线中,与两定点F,F的,且此常数一定要小于|FF|,定义中的“绝<|FF|不可忽视。若=|FF|,则轨迹是以F,F为端点的两条射线,若﹥|FF|,则轨迹不存在。若去掉定义中的绝对值则轨迹仅表示双曲线的一支。
(2)第二定义中要注意定点和定直线是相应的焦点和准线,且“点点距为分子、点线距为分母”,其商即是离心率。圆锥曲线的第二定义,给出了圆锥曲线上的点到焦点距离与此点到相应准线距离间的关系,要善于运用第二定义对它们进行相互转化。
Attention:(1)在求解椭圆、双曲线问题时,首先要判断焦点位置,焦点F,F的位置,是椭圆、双曲线的定位条件,它决定椭圆、双曲线标准方程的类型,而方程中的两个参数,确定椭圆、双曲线的形状和大小,是椭圆、双曲线的定形条件;在求解抛物线问题时,首先要判断开口方向;(2)在椭圆中,最大,,在双曲线中,最大,。
4.圆锥曲线的几何性质:
(1) 椭圆(以②焦点:两个焦点中心(0,0),四个顶点()为例):①范围:;③对称性:两条对称轴;,一个对称,其中长轴长为2,短轴长为2;
④准线:两条准线;
⑤离心率:
,椭圆,越小,椭圆越圆;越大,椭圆越扁。
(2) (2)双曲线(以()为例):①范围:
;③对称性:两条对称轴或,;②焦点:两个焦点
一个对称中心(0,0
),两个顶点,其中实轴长为2,虚轴长为2,特别地,当实轴和虚轴的长相等时,称为等轴双曲线,其方程可设为曲线
;④准线:两条准线,等轴双曲线; ⑤离心率:,双
,越小,开口越小,越大,开口越大;⑥两条渐近线:
(3) 抛物线(以
。 为例):①范围:;②焦点:一个焦点对称轴,其中的几何意义是:焦点到准线的距离;③对称性:一条,没有对称中心,只有一个顶点(0,0
);④准线:一条准线
; ⑤离心率:
,抛物线。
5
、点
和椭圆()的关系:(1
)点在
椭圆外;(2)点
在椭圆上=1;(3)点
在椭圆内
6.直线与圆锥曲线的位置关系:
(1) 相交:直线与椭圆相交;
直线与双曲线相交,但直线与
双曲线相交不一定有,当直线与双曲线的渐近线平行时,直线与双
是直线与双曲线相交的充分条件,但曲线相交且只有一个交点,故
不是必要条件;
有直线与抛物线相交,但直线与抛物线相交不一定,当直线与抛物线的对称轴平行时,直线与抛物线相交且只有一
也仅是直线与抛物线相交的充分条件,但不是必要条件。 个交点,故
Attention:
(1)直线与双曲线、抛物线只有一个公共点时的位置关系有两种情形:相切和相交。如果直线与双曲线的渐近线平行时,直线与双曲线相交,但只有一个交点;如果直线与抛物线的轴平行时,直线与抛物线相交,也只有一个交点;
(2)过双曲线=1外一点的直线与双曲线只有一个公共点的情况如下:①P点在两条渐近线之间且不含双曲线的区域内时,有两条与渐近线平行的直线和分别与双曲线两支相切的两条切线,共四条;②P点在两条渐近线之间且包含双曲线的区域内时,有两条与渐近线平行的直线和只与双曲线一支相切的两条切线,共四条;③P在两条渐近线上但非原点,只有两条:一条是与另一渐近线平行的直线,一条是切线;④P为原点时不存在这样的直线;
(2) 过抛物线外一点总有三条直线和抛物线有且只有一个公共点:两条切线和
一条平行于对称轴的直线。
7、焦半径(圆锥曲线上的点P到焦点F的距离)的计算方法:利用圆锥曲线的
第二定义,转化到相应准线的距离,即焦半径,其中表示P到与F所对应的准线的距离。
8、焦点三角形(椭圆或双曲线上的一点与两焦点所构成的三角形)问题:常利用第一定义和正弦、余弦定理求解。设椭圆或双曲线上的一点
到两焦点的距离分别为,焦点的面积为,
则在椭圆中,
①
=,且
当
即为短轴端点时
,最大
为
=;②
,当即
为短轴端点时,的最
大值为bc;对于双曲线
的焦点三角形有:①
;②
。
9、抛物线中与焦点弦有关的一些几何图形的性质:(1)以过焦点的弦为直径的圆和准线相切;(2)设AB为焦点弦, M为准线与x轴的交点,则∠AMF=∠BMF;(3)设AB为焦点弦,A、B在准线上的射影分别为A,B,若P为AB的中点,则PA⊥PB;(4)若AO的延长线交准线于C,则BC平行于x轴,反之,若过B点平行于x轴的直线交准线于C点,则A,O,C三点共线。
10、弦长公式:若直线
B的横坐标,则=
与圆锥曲线相交于两点A、B,且,若分别为A、=分别为A、B
的纵坐标,则
,若弦AB所在直线方程设为,则=。
特别地,焦点弦(过焦点的弦):焦点弦的弦长的计算,一般不用弦长公式计算,而是将焦点弦转化为两条焦半径之和后,利用第二定义求解。
11、圆锥曲线的中点弦问题:遇到中点弦问题常用“韦达定理”或“点差法”求解。在椭圆中,以为中点的弦所在直线的斜率k=-;在双曲线中,以为中点的弦所在直线的斜率
k=;在抛物线中,以为中点的弦所在直线的斜率k=。 Attention:因为是直线与圆锥曲线相交于两点的必要条件,故在求解有关! 弦长、对称问题时,务必别忘了检验
12.重要结论:
(1)双曲线的渐近线方程为;
(2)
以为渐近线(即与双
曲线共渐近线)的双曲线
方程为为参数,≠0)。
如与双曲线有共同的渐近线,且过点的双曲线方程为_______(
答:
)
(3)中心在原点,坐标轴为对称轴的椭圆、双曲线方程可设为;
(4)椭圆、双曲线的通径(过焦点且垂直于对称轴的弦)为,焦准距(焦点到相应准线的距离)为,抛物线的通径为,焦准距为;
(5)通径是所有焦点弦(过焦点的弦)中最短的弦;
(6)若抛物
线的焦点弦为AB
,,则①;②
(7)若OA、OB是过抛物线 顶点O的两条互相垂直的弦,则直线AB恒经过定点
第二篇:高中数学圆锥曲线知识点总结
圆锥曲线
1.定义和方程
(1)椭圆: (
( )表示焦点在
)表示焦点在 轴上;
轴上;
 (
( )表示焦点在
)表示焦点在 轴上.
轴上.
(2)双曲线: (
( ,
, )表示焦点在
)表示焦点在 轴上;
轴上;
 (
( ,
, )表示焦点在
)表示焦点在 轴上.
轴上.
(3)抛物线: (焦点在
(焦点在 轴上),
轴上),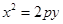 (焦点在
(焦点在 轴上)
轴上)
2.几何性质
(1)离心率:

(2)通径:过焦点作与焦点所在坐标轴垂直的直线与曲线两个交点的距离

(3)焦点三角形:椭圆(或双曲线)上一点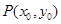 与两焦点形成的三角形,记
与两焦点形成的三角形,记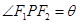

(4)渐近线: (
( ,
, )的渐近线方程为
)的渐近线方程为
与 具有相同渐近线的双曲线方程:
具有相同渐近线的双曲线方程:
等轴双曲线:实轴与虚轴长相等, ,离心率
,离心率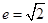
共轭双曲线:实虚对调, 的共轭双曲线是
的共轭双曲线是
 (5)抛物线的焦半径:
(5)抛物线的焦半径:
① ,
,
② ,
,
(6)弦中点问题(点差法)
直线 与
与 (
( )交于
)交于 ,
,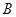 两点,
两点, 的中点为
的中点为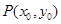 ,则
,则
直线 与
与 (
( ,
, )交于
)交于 ,
,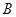 两点,
两点, 的中点为
的中点为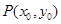 ,则
,则
直线 与
与 交于
交于 ,
,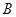 两点,
两点, 的中点为
的中点为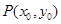 ,则
,则
(7)弦长公式
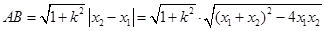 或
或
-
高中数学圆锥曲线知识点总结
高中数学知识点大全圆锥曲线一考点限考概要1椭圆1轨迹定义定义一在平面内到两定点的距离之和等于定长的点的轨迹是椭圆两定点是焦点两定点…
-
高中数学_圆锥曲线知识点小结
助飞教育圆锥曲线知识点小结一椭圆1椭圆的定义平面内与两个定点F1F2的距离的和等于常数大于其中两个定点叫做椭圆的焦点焦点间的距离叫…
-
高二圆锥曲线知识点总结与例题
高二圆锥曲线知识点总结与例题分析一椭圆1椭圆概念平面内与两个定点F1F2的距离的和等于常数2a大于F1F2的点的轨迹叫做椭圆这两个…
-
高中数学 圆锥曲线知识点小结
《圆锥曲线》知识点小结一、椭圆:(1)椭圆的定义:平面内与两个定点F1,F2的距离的和等于常数(大于|F1F2|)的点的轨迹。其中…
-
高中数学圆锥曲线知识点总结
高中数学知识点大全圆锥曲线一考点限考概要1椭圆1轨迹定义定义一在平面内到两定点的距离之和等于定长的点的轨迹是椭圆两定点是焦点两定点…
-
圆锥曲线知识点总结(绝对物超所值)
圆锥曲线的方程与性质1.椭圆(1)椭圆概念平面内与两个定点F1、F2的距离的和等于常数2a(大于|F1F2|)的点的轨迹叫做椭圆。…
-
高考数学复习知识点总结——圆锥曲线
高中数学圆锥曲线方程§08.圆锥曲线方程知识要点一、椭圆方程.1.椭圆方程的第一定义:PF1?PF2?2a?F1F2方程为椭圆,P…
-
圆锥曲线知识点总结
高中数学圆锥曲线选知识点总结一、椭圆1、定义:平面内与两个定点F1,F2的距离之和等于常数(大于F1F2)的点的轨迹称为椭圆.即:…
-
高中数学圆锥曲线解题技巧方法总结[1]
圆锥曲线1.圆锥曲线的两定义:第一定义中要重视“括号”内的限制条件:椭圆中,与两个定点F1,F2的距离的和等于常数2a,且此常数2…
-
完美版圆锥曲线知识点总结
圆锥曲线的方程与性质1椭圆1椭圆概念平面内与两个定点F1F2的距离的和等于常数2a大于F1F2的点的轨迹叫做椭圆这两个定点叫做椭圆…
-
圆锥曲线基础知识汇总表
常用经验公式1.圆的切线方程(1)已知圆x2?y2?Dx?Ey?F?0.①若已知切点(x0,y0)在圆上,则切线只有一条,其方程是…