数学必修五知识点总结归纳
高中数学必修5知识点
1、正弦定理:在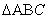 中,
中, 、
、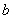 、
、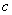 分别为角
分别为角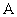 、
、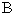 、
、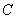 的对边,
的对边,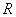 为
为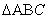 的外接圆的半径,则有
的外接圆的半径,则有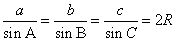 .
.
2、正弦定理的变形公式:①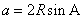 ,
,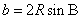 ,
,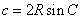 ;
;
②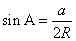 ,
,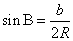 ,
,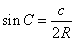 ;
;
③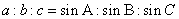 ;
;
④ .
.
3、三角形面积公式: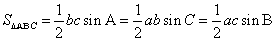 .
.
4、余弦定理:在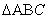 中,有
中,有 ,
,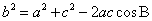 ,
,
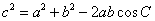 .
.
5、余弦定理的推论: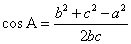 ,
,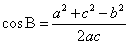 ,
,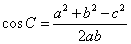 .
.
6、设 、
、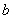 、
、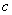 是
是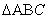 的角
的角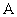 、
、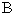 、
、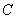 的对边,则:①若
的对边,则:①若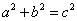 ,则
,则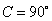 ;
;
②若 ,则
,则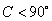 ;③若
;③若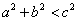 ,则
,则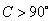 .
.
7、数列:按照一定顺序排列着的一列数.
8、数列的项:数列中的每一个数.
9、有穷数列:项数有限的数列.
10、无穷数列:项数无限的数列.
11、递增数列:从第2项起,每一项都不小于它的前一项的数列.
12、递减数列:从第2项起,每一项都不大于它的前一项的数列.
13、常数列:各项相等的数列.
14、摆动数列:从第2项起,有些项大于它的前一项,有些项小于它的前一项的数列.
15、数列的通项公式:表示数列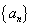 的第
的第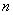 项与序号
项与序号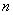 之间的关系的公式.
之间的关系的公式.
16、数列的递推公式:表示任一项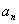 与它的前一项
与它的前一项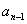 (或前几项)间的关系的公式.
(或前几项)间的关系的公式.
17、如果一个数列从第2项起,每一项与它的前一项的差等于同一个常数,则这个数列称为等差数列,这个常数称为等差数列的公差.
18、由三个数 ,
,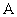 ,
,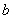 组成的等差数列可以看成最简单的等差数列,则
组成的等差数列可以看成最简单的等差数列,则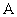 称为
称为 与
与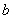 的等差中项.若
的等差中项.若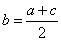 ,则称
,则称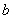 为
为 与
与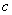 的等差中项.
的等差中项.
19、若等差数列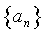 的首项是
的首项是 ,公差是
,公差是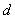 ,则
,则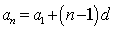 .
.
20、通项公式的变形:①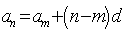 ;②
;②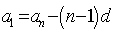 ;③
;③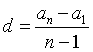 ;
;
④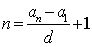 ;⑤
;⑤ .
.
21、若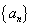 是等差数列,且
是等差数列,且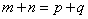 (
(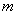 、
、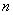 、
、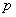 、
、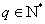 ),则
),则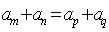 ;若
;若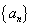 是等差数列,且
是等差数列,且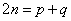 (
(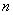 、
、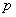 、
、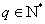 ),则
),则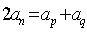 .
.
22、等差数列的前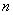 项和的公式:①
项和的公式:①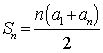 ;②
;② .
.
23、等差数列的前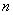 项和的性质:①若项数为
项和的性质:①若项数为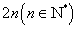 ,则
,则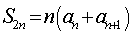 ,且
,且 ,
,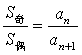 .
.
②若项数为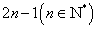 ,则
,则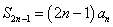 ,且
,且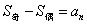 ,
,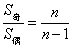 (其中
(其中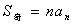 ,
,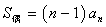 ).
).
24、如果一个数列从第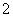 项起,每一项与它的前一项的比等于同一个常数,则这个数列称为等比数列,这个常数称为等比数列的公比.
项起,每一项与它的前一项的比等于同一个常数,则这个数列称为等比数列,这个常数称为等比数列的公比.
25、在 与
与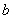 中间插入一个数
中间插入一个数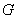 ,使
,使 ,
,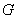 ,
,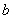 成等比数列,则
成等比数列,则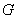 称为
称为 与
与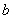 的等比中项.若
的等比中项.若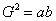 ,则称
,则称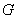 为
为 与
与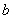 的等比中项.
的等比中项.
26、若等比数列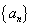 的首项是
的首项是 ,公比是
,公比是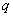 ,则
,则 .
.
27、通项公式的变形:①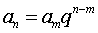 ;②
;②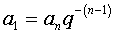 ;③
;③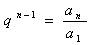 ;④
;④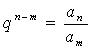 .
.
28、若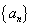 是等比数列,且
是等比数列,且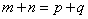 (
(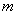 、
、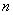 、
、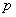 、
、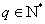 ),则
),则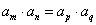 ;若
;若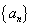 是等比数列,且
是等比数列,且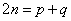 (
(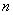 、
、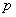 、
、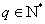 ),则
),则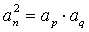 .
.
29、等比数列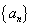 的前
的前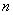 项和的公式:
项和的公式: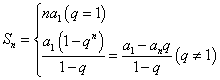 .
.
30、等比数列的前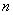 项和的性质:①若项数为
项和的性质:①若项数为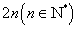 ,则
,则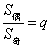 .
.
②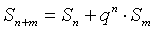 .
.
③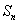 ,
,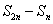 ,
,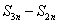 成等比数列.
成等比数列.
31、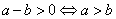 ;
;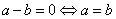 ;
;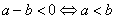 .
.
32、不等式的性质: ①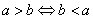 ;②
;②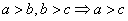 ;③
;③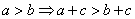 ;
;
④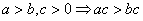 ,
,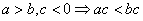 ;⑤
;⑤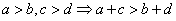 ;
;
⑥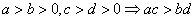 ;⑦
;⑦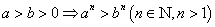 ;
;
⑧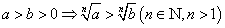 .
.
33、一元二次不等式:只含有一个未知数,并且未知数的最高次数是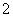 的不等式.
的不等式.
34、二次函数的图象、一元二次方程的根、一元二次不等式的解集间的关系:
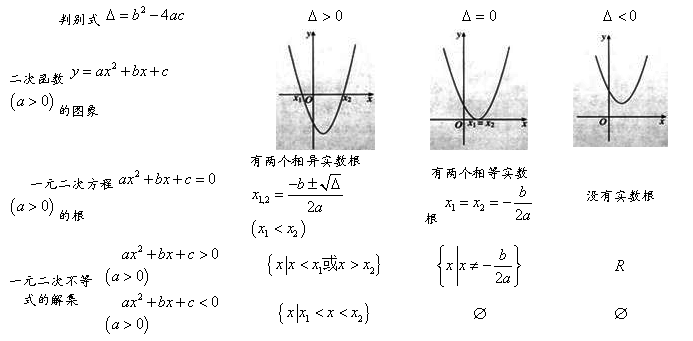
35、二元一次不等式:含有两个未知数,并且未知数的次数是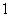 的不等式.
的不等式.
36、二元一次不等式组:由几个二元一次不等式组成的不等式组.
37、二元一次不等式(组)的解集:满足二元一次不等式组的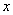 和
和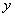 的取值构成有序数对
的取值构成有序数对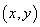 ,所有这样的有序数对
,所有这样的有序数对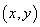 构成的集合.
构成的集合.
38、在平面直角坐标系中,已知直线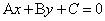 ,坐标平面内的点
,坐标平面内的点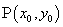 .
.
①若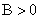 ,
,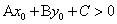 ,则点
,则点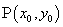 在直线
在直线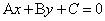 的上方.
的上方.
②若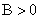 ,
,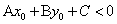 ,则点
,则点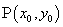 在直线
在直线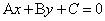 的下方.
的下方.
39、在平面直角坐标系中,已知直线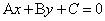 .
.
①若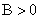 ,则
,则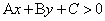 表示直线
表示直线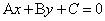 上方的区域;
上方的区域;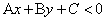 表示直线
表示直线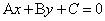 下方的区域.
下方的区域.
②若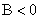 ,则
,则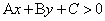 表示直线
表示直线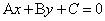 下方的区域;
下方的区域;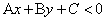 表示直线
表示直线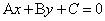 上方的区域.
上方的区域.
40、线性约束条件:由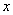 ,
,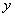 的不等式(或方程)组成的不等式组,是
的不等式(或方程)组成的不等式组,是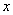 ,
,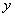 的线性约束条件.
的线性约束条件.
目标函数:欲达到最大值或最小值所涉及的变量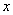 ,
,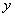 的解析式.
的解析式.
线性目标函数:目标函数为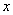 ,
,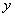 的一次解析式.
的一次解析式.
线性规划问题:求线性目标函数在线性约束条件下的最大值或最小值问题.
可行解:满足线性约束条件的解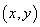 .
.
可行域:所有可行解组成的集合.
最优解:使目标函数取得最大值或最小值的可行解.
41、设 、
、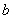 是两个正数,则
是两个正数,则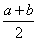 称为正数
称为正数 、
、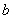 的算术平均数,
的算术平均数,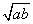 称为正数
称为正数 、
、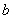 的几何平均数.
的几何平均数.
42、均值不等式定理: 若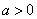 ,
,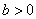 ,则
,则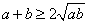 ,即
,即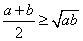 .
.
43、常用的基本不等式:①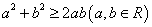 ;②
;②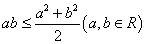 ;
;
③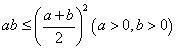 ;④
;④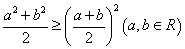 .
.
44、极值定理:设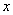 、
、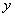 都为正数,则有
都为正数,则有
⑴若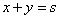 (和为定值),则当
(和为定值),则当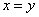 时,积
时,积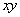 取得最大值
取得最大值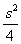 .
.
⑵若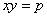 (积为定值),则当
(积为定值),则当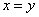 时,和
时,和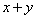 取得最小值
取得最小值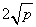 .
.
第二篇:必修五第二章数列归纳总结
必修五第二章数列归纳总结
一、数列
1.数列的定义
数列是按一定次序排成的一列数,从函数观点看,数列是定义域为正整数集(或它的有限子集)的函数f(n),当自变量n从1开始依次取正整数时所对应的一列函数值f(1),f(2),…,f(n),….通常用an代替f(n).于是数列的一般形式为a1,a2,…,an,…,简记为{an}.
一、数列
1.数列的定义
数列是按一定次序排成的一列数,从函数观点看,数列是定义域为正整数集(或它的有限子集)的函数f(n),当自变量n从1开始依次取正整数时所对应的一列函数值f(1),f(2),…,f(n),….通常用an代替f(n).于是数列的一般形式为a1,a2,…,an,…,简记为{an}.
3.an与Sn的关系
设Sn=a1+a2+a3+…+an,
则an=
二、等差数列
1.等差数列的定义
如果一个数列从第二项起,每一项与它的前一项的差都等于同一个常数,这样的数列叫做等差数列.
2.等差中项
如果三数a、A、b成等差数列,则A叫做a和b的等差中项,∴A=.
3.(1)通项公式
an=a1+(n-1)d.
推导方法:累加法an=(an-an-1)+(an-1-an-2)+…+(a2-a1)+a1.
(2)前n项和公式
Sn==na1+d.
推导方法:倒序相加法.
4.用函数观点认识等差数列
(1)an=nd+(a1-d)是n的一次函数.
(2)Sn=n2+(a1-)n,是关于n的常数项为零的二次函数.
5.等差数列的判定方法
(1)定义法:an+1-an=d(常数)(n∈N*)?{an}是等差数列;
(2)中项公式法:2an+1=an+an+2(n∈N*)?{an}是等差数列;
(3)通项公式法:an=kn+b(k,b是常数)(n∈N*)?{an}是等差数列;
(4)前n项和公式法:Sn=An2+Bn(A、B是常数)(n∈N*)?{an}是等差数列.
(5){an}是等差数列?{}是等差数列
6.等差数列的性质
(1)下标和与项的和的关系
在等差数列中,若p+q=m+n,则有ap+aq=am+an;若2m=p+q,则有2am=ap+aq,(p,q,m,n∈N*).
(2)任意两项的关系
在等差数列{an}中,m、n∈N*,则am-an=(m-n)d或am=an+(m-n)d或=d.
(3)在等差数列中,等距离取出若干项也构成一个等差数列,即an,an+m,an+2m,…为等差数列,公差为md.
等差数列的依次n项的和也构成一个等差数列,即Sn,S2n-Sn,S3n-S2n,……为等差数列,公差为n2d.
即下标成等差的项成等差数列,下标和成等差的具有相同构成规律的项的和成等差数列.
(4)设等差数列{an}的公差为d,那么
d>0?{an}是递增数列;d<0?{an}是递减数列;d=0?{an}是常数数列.
(5)①数列{λan+b}仍为等差数列,公差为λd.
若{bn},{an}都是等差数列,则{an±bn}仍为等差数列,{λ1an+λ2bn}(λ1,λ2为常数)也是等差数列.
②项数为n的等差数列中,n为奇数时,设m=,则S奇-S偶=am,=,Sn=na中=nam.
n为偶数时,S偶-S奇=d.
③若{an}与{bn}为等差数列,且前n项和分别为Sn与S′n,则=.
④等差数列{an}中,若an=m,am=n(m≠n),则am+n=0.
⑤若数列{an}的前p项和为Sp=q,前q项和为Sq=p(p≠q),则Sp+q=-(p+q).
⑥若数列{an}的前n项和为Sn,Sp=Sq(p≠q),则Sp+q=0.
三、等比数列
1.等比数列的定义
一般地,如果一个数列从第2项起,每一项与它的前一项的比等于同一个常数,这个数列就叫做等比数列.
2.等比中项
如果三个数a、G、b成等比数列,那么G叫做a和b的等比中项,即G2=ab.
3.等比数列的通项公式
an=a1·qn-1(n∈N*).
推导方法:累乘法:·……·=qn-1.
4.等比数列的前n项和
当q=1时,Sn=na1,
当q≠1时.Sn==.
推导方法:乘公比、错位相减法.
5.等比数列的判定方法
(1)an+1=anq(q是不为0的常数,n∈N*,an≠0)?{an}是等比数列.
(2)an=cqn-1(c,q均是不为0的常数,n∈N*)?{an}是等比数列.
(3)an+12=an·an+2(an≠0,n∈N*)?{an}是等比数列.
(4)Sn=A·qn-A(A、q为常数且A≠0,q≠0,1)?{an}是公比不为1的等比数列.
6.等比数列的主要性质
(1)下标和与项的积的关系
在等比数列{an}中,若m、n、p、q∈N*且m+n=p+q,则am·an=ap·aq.特别地,若2m=p+q,则ap·aq=am2;a1an=a2an-1=a3an-2=….
(2)任意两项的关系
若{an}为等比数列,则=qm-n或am=an·qm-n(m、n∈N*).
(3)等间隔的k项和(或积)仍成等比数列.
例如:{an}是等比数列,则
①a1,a3,a5,…,a2n-1;②a1+a2,a2+a3,a3+a4,…;③a1a2,a2a3,a3a4,…;④a1+a2,a3+a4,a5+a6……均成等比数列.
(4)等比数列{an}的单调性
当,或时,{an}为递增数列;当或时,{an}为递减数列.
(5)①{an}是等比数列?{c·an}是等比数列(c≠0).
②{an}、{bn}均为等比数列?{an·bn}、{}仍是等比数列.
③若{an}是等比数列,则{an2}、{}(an>0)、{}、{|an|}均为等比数列.
④非零常数列既是等差数列,也是等比数列.
⑤若{an}是等差数列,则{ban}是等比数列.
若{an}是正项等比数列,则{lgan}是等差数列.
误区警示
1.数列与数集应予区别,数列中的数排列有序,数集中的元素无序;数列中的数可重复出现,数集中的元素互异.
2.并不是每一个数列都有通项公式,给出前n项时,写出的通项公式可以不止一个.
3.已知{an}的前n项和Sn求an时,
用an=求解应注意分类讨论.
an=Sn-Sn-1是在n≥2条件下求出的,应检验a1是否适合.如果适合,则合写在一块,如果不适合,则分段表示.千万注意用an=Sn-Sn-1判断数列{an}是否为等差(或等比)数列时,不要忘记验证a1是否满足.
如:Sn=n2+n时,{an}是等差数列.
Sn=n2+n+1时,{an}不是等差数列.
Sn=2n-1时,{an}是等比数列.
Sn=2n+1时,{an}不是等比数列.
4.在讨论等差数列{an}的前n项和Sn的最值时,不要忽视n是整数的条件及含0项的情形.
如:在等差数列{an}中,已知a1=20,前n项和为Sn,且如S10=S15,求当n取何值时,Sn有最大值,并求出它的最大值.取最大值的应为S12和S13.
5.G是a、b的等比中项?/?/ G=.
6.在应用等比数列的前n项和公式时,一定要对q=1与q≠1进行分类讨论.
7.等比数列中隐含着各项不为零、公比不为零,项与公比的符号有着密切的联系,解题时应特别注意.
-
数学必修五知识点总结归纳
必修五知识点总结归纳一解三角形1正弦定理在C中abc分别为角C的对边R为C的外abc2RsinsinsinC正弦定理的变形公式a2…
-
高中数学必修五(人教版)知识点总结。
高中数学必修5知识点一解三角形1正弦定理在C中abc分别为角C的对边R为C的外接圆的半径则有asinbsina2RcsinC2R正…
-
高一数学知识点总结--必修5
高中数学必修5知识点第一章:解三角形1、正弦定理:在???C中,a、b、c分别为角?、?、C的对边,R为???C的外接圆的半径,则…
-
人教版数学必修五知识点总结
一三角形中的三角函数1内角和定理三角形三角和为任意两角和与第三个角总互补任意两半角和与第三个角的半角总互余锐角三角形三内角都是锐角…
-
人教版数学必修五知识点总结
第一章解三角形1、内角和定理:(1)三角形三角和为?,任意两角和与第三个角总互补,任意两半角和与第三个角的半角总互余.(2)锐角三…
-
高中数学必修五 第一章 解三角形知识点归纳及测试卷
高中数学必修五第一章解三角形知识点归纳1、三角形三角关系:A+B+C=180;C=180(A+B);2、三角形三边关系:a+b>c…
-
高二数学必修五_第二章_等差等比数列练习题以及基础知识点总结_经典版
基础知识点(一)知识归纳:1.概念与公式:①等差数列:1°.定义:若数列{an}满足an?1?an?d(常数),则{an}称等差数…
-
高一数学知识点总结--必修5
高中数学必修5知识点第一章:解三角形1、正弦定理:在???C中,a、b、c分别为角?、?、C的对边,R为???C的外接圆的半径,则…
-
数学必修五知识点总结归纳
必修五知识点总结归纳一解三角形1正弦定理在C中abc分别为角C的对边R为C的外abc2RsinsinsinC正弦定理的变形公式a2…
-
高中数学必修五(人教版)知识点总结。
高中数学必修5知识点一解三角形1正弦定理在C中abc分别为角C的对边R为C的外接圆的半径则有asinbsina2RcsinC2R正…
-
高一英语必修2第5单元短语知识点归纳和总结
高一英语必修2第5单元短语和知识点归纳和总结一、重点短语归纳和总结1.dream_________梦见;梦想;设想2.______…