高中数学导数知识点归纳总结
高中导数知识点归纳
一、基本概念
1. 导数的定义:
设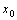 是函数
是函数 定义域的一点,如果自变量
定义域的一点,如果自变量 在
在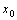 处有增量
处有增量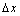 ,则函数值
,则函数值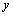 也引起相应的增量
也引起相应的增量 ;比值
;比值 称为函数
称为函数 在点
在点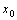 到
到 之间的平均变化率;如果极限
之间的平均变化率;如果极限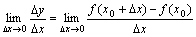 存在,则称函数
存在,则称函数 在点
在点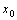 处可导,并把这个极限叫做
处可导,并把这个极限叫做 在
在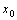 处的导数。
处的导数。
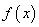 在点
在点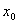 处的导数记作
处的导数记作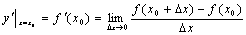
2 导数的几何意义:(求函数在某点处的切线方程)
函数 在点
在点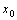 处的导数的几何意义就是曲线
处的导数的几何意义就是曲线 在点
在点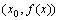 处的切线的斜率,也就是说,曲线
处的切线的斜率,也就是说,曲线 在点P
在点P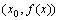 处的切线的斜率是
处的切线的斜率是 ,切线方程为
,切线方程为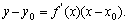
3.基本常见函数的导数:
① (C为常数) ②
(C为常数) ②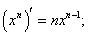
③ ; ④
; ④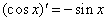 ;
;
⑤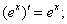 ⑥
⑥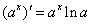 ;
;
⑦ ; ⑧
; ⑧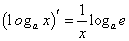 .
.
二、导数的运算
1.导数的四则运算:
法则1:两个函数的和(或差)的导数,等于这两个函数的导数的和(或差),
即: 
法则2:两个函数的积的导数,等于第一个函数的导数乘以第二个函数,加上第一个
函数乘以第二个函数的导数,即: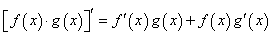
常数与函数的积的导数等于常数乘以函数的导数: 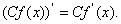 (
( 为常数)
为常数)
法则3:两个函数的商的导数,等于分子的导数与分母的积,减去分母的导数与分子的积,再除以分母的平方: 。
。
2.复合函数的导数
形如 的函数称为复合函数。法则:
的函数称为复合函数。法则:  .
.
三、导数的应用
1.函数的单调性与导数
(1)设函数 在某个区间
在某个区间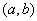 可导,
可导,
如果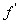

 ,则
,则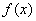 在此区间上为增函数;
在此区间上为增函数;
如果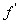
 ,则
,则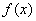 在此区间上为减函数。
在此区间上为减函数。
(2)如果在某区间内恒有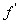
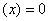 ,则
,则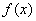 为常函数。
为常函数。
2.函数的极点与极值:当函数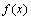 在点
在点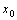 处连续时,
处连续时,
①如果在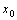 附近的左侧
附近的左侧 >0,右侧
>0,右侧 <0,那么
<0,那么 是极大值;
是极大值;
②如果在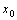 附近的左侧
附近的左侧 <0,右侧
<0,右侧 >0,那么
>0,那么 是极小值.
是极小值.
3.函数的最值:
一般地,在区间 上连续的函数
上连续的函数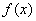 在
在 上必有最大值与最小值。函数
上必有最大值与最小值。函数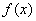
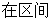
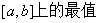
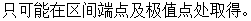
求函数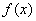
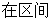
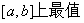 的一般步骤:①求函数
的一般步骤:①求函数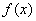 的导数,令导数
的导数,令导数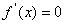 解出方程的跟②在区间
解出方程的跟②在区间 列出
列出 的表格,求出极值及
的表格,求出极值及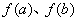 的值;③比较端点及极值点处的函数值的大小,从而得出函数的最值
的值;③比较端点及极值点处的函数值的大小,从而得出函数的最值
4.相关结论总结:
①可导的奇函数函数其导函数为偶函数.
②可导的偶函数函数其导函数为奇函数.
四、例题插播
例1:函数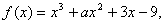 已知
已知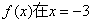 时取得极值,则
时取得极值,则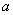 = ( )
= ( )
A.2 B.3 C.4 D.5
例2. 已知函数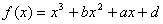 的图像过点P(0,2),且在点M
的图像过点P(0,2),且在点M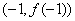 处的切线方程为
处的切线方程为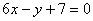 .(Ⅰ)求函数
.(Ⅰ)求函数 的解析式;(Ⅱ)求函数
的解析式;(Ⅱ)求函数 的单调区间.
的单调区间.
第二篇:高中数学第十四章导数知识点
高中数学第十四章 导数
考试内容:
数学探索©版权所有www.delve.cn导数的背影.
数学探索©版权所有www.delve.cn导数的概念.
数学探索©版权所有www.delve.cn多项式函数的导数.
数学探索©版权所有www.delve.cn利用导数研究函数的单调性和极值.函数的最大值和最小值.
数学探索©版权所有www.delve.cn考试要求:
数学探索©版权所有www.delve.cn(1)了解导数概念的某些实际背景.
数学探索©版权所有www.delve.cn(2)理解导数的几何意义.
数学探索©版权所有www.delve.cn(3)掌握函数,y=c(c为常数)、y=xn(n∈N+)的导数公式,会求多项式函数的导数.
数学探索©版权所有www.delve.cn(4)理解极大值、极小值、最大值、最小值的概念,并会用导数求多项式函数的单调区间、极大值、极小值及闭区间上的最大值和最小值.
数学探索©版权所有www.delve.cn(5)会利用导数求某些简单实际问题的最大值和最小值.
§14. 导数 知识要点

1. 导数(导函数的简称)的定义:设 是函数
是函数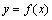 定义域的一点,如果自变量
定义域的一点,如果自变量 在
在 处有增量
处有增量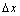 ,则函数值
,则函数值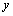 也引起相应的增量
也引起相应的增量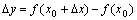 ;比值
;比值 称为函数
称为函数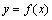 在点
在点 到
到 之间的平均变化率;如果极限
之间的平均变化率;如果极限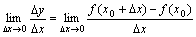 存在,则称函数
存在,则称函数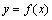 在点
在点 处可导,并把这个极限叫做
处可导,并把这个极限叫做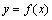 在
在 处的导数,记作
处的导数,记作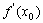 或
或 ,即
,即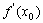 =
=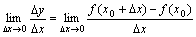 .
.
注:①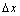 是增量,我们也称为“改变量”,因为
是增量,我们也称为“改变量”,因为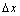 可正,可负,但不为零.
可正,可负,但不为零.
②以知函数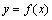 定义域为
定义域为 ,
, 的定义域为
的定义域为 ,则
,则 与
与 关系为
关系为 .
.
2. 函数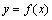 在点
在点 处连续与点
处连续与点 处可导的关系:
处可导的关系:
⑴函数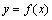 在点
在点 处连续是
处连续是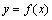 在点
在点 处可导的必要不充分条件.
处可导的必要不充分条件.
可以证明,如果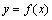 在点
在点 处可导,那么
处可导,那么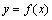 点
点 处连续.
处连续.
事实上,令 ,则
,则 相当于
相当于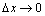 .
.
于是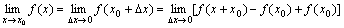
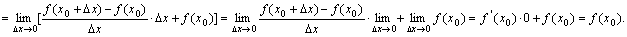 ⑵如果
⑵如果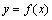 点
点 处连续,那么
处连续,那么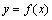 在点
在点 处可导,是不成立的.
处可导,是不成立的.
例: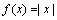 在点
在点 处连续,但在点
处连续,但在点 处不可导,因为
处不可导,因为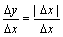 ,当
,当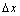 >0时,
>0时, ;当
;当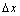 <0时,
<0时, ,故
,故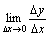 不存在.
不存在.
注:①可导的奇函数函数其导函数为偶函数.
②可导的偶函数函数其导函数为奇函数.
3. 导数的几何意义:
函数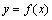 在点
在点 处的导数的几何意义就是曲线
处的导数的几何意义就是曲线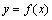 在点
在点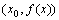 处的切线的斜率,也就是说,曲线
处的切线的斜率,也就是说,曲线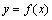 在点P
在点P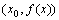 处的切线的斜率是
处的切线的斜率是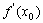 ,切线方程为
,切线方程为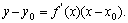
4. 求导数的四则运算法则:


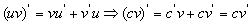 (
(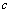 为常数)
为常数)

注:①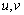 必须是可导函数.
必须是可导函数.
②若两个函数可导,则它们和、差、积、商必可导;若两个函数均不可导,则它们的和、差、积、商不一定不可导.
例如:设 ,
,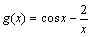 ,则
,则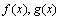 在
在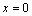 处均不可导,但它们和
处均不可导,但它们和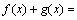
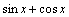 在
在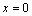 处均可导.
处均可导.
5. 复合函数的求导法则: 或
或
复合函数的求导法则可推广到多个中间变量的情形.
6. 函数单调性:
⑴函数单调性的判定方法:设函数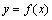 在某个区间内可导,如果
在某个区间内可导,如果 >0,则
>0,则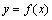 为增函数;如果
为增函数;如果 <0,则
<0,则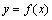 为减函数.
为减函数.
⑵常数的判定方法;
如果函数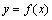 在区间
在区间 内恒有
内恒有 =0,则
=0,则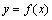 为常数.
为常数.
注:① 是f(x)递增的充分条件,但不是必要条件,如
是f(x)递增的充分条件,但不是必要条件,如 在
在 上并不是都有
上并不是都有 ,有一个点例外即x=0时f(x) = 0,同样
,有一个点例外即x=0时f(x) = 0,同样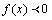 是f(x)递减的充分非必要条件.
是f(x)递减的充分非必要条件.
②一般地,如果f(x)在某区间内有限个点处为零,在其余各点均为正(或负),那么f(x)在该区间上仍旧是单调增加(或单调减少)的.
7. 极值的判别方法:(极值是在 附近所有的点,都有
附近所有的点,都有 <
<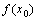 ,则
,则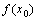 是函数
是函数 的极大值,极小值同理)
的极大值,极小值同理)
当函数 在点
在点 处连续时,
处连续时,
①如果在 附近的左侧
附近的左侧 >0,右侧
>0,右侧 <0,那么
<0,那么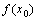 是极大值;
是极大值;
②如果在 附近的左侧
附近的左侧 <0,右侧
<0,右侧 >0,那么
>0,那么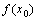 是极小值.
是极小值.
也就是说 是极值点的充分条件是
是极值点的充分条件是 点两侧导数异号,而不是
点两侧导数异号,而不是 =0①. 此外,函数不可导的点也可能是函数的极值点②.当然,极值是一个局部概念,极值点的大小关系是不确定的,即有可能极大值比极小值小(函数在某一点附近的点不同).
=0①. 此外,函数不可导的点也可能是函数的极值点②.当然,极值是一个局部概念,极值点的大小关系是不确定的,即有可能极大值比极小值小(函数在某一点附近的点不同).
注①: 若点 是可导函数
是可导函数 的极值点,则
的极值点,则 =0. 但反过来不一定成立. 对于可导函数,其一点
=0. 但反过来不一定成立. 对于可导函数,其一点 是极值点的必要条件是若函数在该点可导,则导数值为零.
是极值点的必要条件是若函数在该点可导,则导数值为零.
例如:函数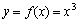 ,
,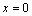 使
使 =0,但
=0,但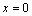 不是极值点.
不是极值点.
②例如:函数 ,在点
,在点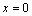 处不可导,但点
处不可导,但点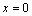 是函数的极小值点.
是函数的极小值点.
8. 极值与最值的区别:极值是在局部对函数值进行比较,最值是在整体区间上对函数值进行比较.
注:函数的极值点一定有意义.
9. 几种常见的函数导数:
I. (
(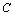 为常数)
为常数) 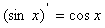

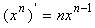 (
( )
) 

II. 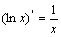
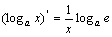
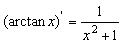



III. 求导的常见方法:
①常用结论: .
.
②形如 或
或 两边同取自然对数,可转化求代数和形式.
两边同取自然对数,可转化求代数和形式.
③无理函数或形如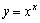 这类函数,如
这类函数,如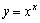 取自然对数之后可变形为
取自然对数之后可变形为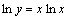 ,对两边求导可得
,对两边求导可得 .
.
-
高中数学导数知识点归纳总结
核心出品必属精品免费下载导数考试内容:导数的背影.导数的概念.多项式函数的导数.利用导数研究函数的单调性和极值.函数的最大值和最小…
-
高中数学导数知识点归纳总结
高中导数知识点归纳一基本概念1导数的定义设x0是函数yfx定义域的一点如果自变量x在x0处有增量x则函数值y也引起相应的增量yfx…
-
高中导数及其应用知识点归纳(总结得很好,实用)
第三章导数及其应用3.1.2导数的概念(要求熟悉)1.函数f(x)在x?x0处的导数:函数y?f(x)在x?x0处的瞬时变化率称为…
-
高中数学导数知识点归纳总结
§14.导数知识要点1.导数(导函数的简称)的定义:设x0是函数y?f(x)定义域的一点,如果自变量x在x0处有增量?x,则函数值…
-
高中数学导数知识点归纳
高中数学选修22知识点第一章导数及其应用一导数概念的引入1导数的物理意义瞬时速率一般的函数yfx在xx0处的瞬时变化率是x0lim…
-
高中导数及其应用知识点归纳(总结得很好,实用)
第三章导数及其应用3.1.2导数的概念(要求熟悉)1.函数f(x)在x?x0处的导数:函数y?f(x)在x?x0处的瞬时变化率称为…
-
1、20xx高考文科数学:导数知识点总结
、20xx高考文科数学:导数知识点总结(4)(cosx)???sinx.(5)(lnx)??'''exxxxx;(loga)??l…
-
高中数学人教版选修2-2导数及其应用知识点总结
数学选修2-2导数及其应用知识点必记1.函数的平均变化率是什么?答:平均变化率为f(x2)?f(x1)f(x1??x)?f(x1)…
-
高中数学导数知识点归纳总结
§14.导数知识要点1.导数(导函数的简称)的定义:设x0是函数y?f(x)定义域的一点,如果自变量x在x0处有增量?x,则函数值…
-
高中数学人教版选修2-2导数及其应用(定积分)知识点总结
数学选修2-2导数及其应用(定积分)知识点必记1.函数的平均变化率是什么?答:平均变化率为f(x2)?f(x1)f(x1??x)?…
-
高中数学理科选修2-2知识点总结
第一章导数及其应用一.导数概念的引入1.导数的物理意义:瞬时速率。一般的,函数y?f(x)在x?x0处的瞬时变化率是?x?0lim…