导数作为微分学的中的一个基本概念，是一个非常重要的组成部分。导数的计算与应用也是数学上的重点与难点。下面我将就如何求导数做一总结。

一、引例

1、小学时我们所学的速度被描述为所经过的路程与所花的时间的比值，并说该点做匀速运动。此时我们引入公式s-s0/t-t0=f(t)-f(t0)/t-t0。如果令t-t0,，取该式极限得v=limf(t)-f(t0)/t-t0，这时就把这个极限值v称为动点在该时刻t0的瞬时速度。

2、设有曲线Ｃ及Ｃ上一点Ｍ，在点Ｍ外令取Ｃ上一点Ｎ，作割线ＭＮ。当点Ｎ沿曲线Ｃ趋于点M时，如果割线ＭＮ绕点Ｍ旋转而趋于极限位置ＭＴ，直线ＭＴ就称为曲线Ｃ在点Ｍ处的切线。于是割线MN的斜率为tanx=

设为k，即

K=limx?x0f x ?f(x0)

x?x0y?y0f x ?f x0 x?x0x?x0x——x0时，上式的极限存在，

存在，则此极限k是割线斜率的极限，也就是切线的斜率。

二、导数的定义

设函数y=f(x)在点x0的某个邻域内有定义，当自变量x在x0处取得增量?X(点x0+?x仍在该领域内)时，相应的函数取得增量

?y=f(x0+?x)-f(x0);如果?y与?x之比当?x→0时的极限存在，则称函数y=f(x)在点x0处可导，并称这个极限为函数y=f(x)在点x0处的导数，记为f’(x0),即

f’(x0)=lim?x→0?y

?xlim?x→0f(x0+?x)?f(x0)

?x,也可记作y’｜x=x,dyx=x dx00

或df(x)dxx=x0

 

第二篇：导数总结

导数专题

一．本章知识结构

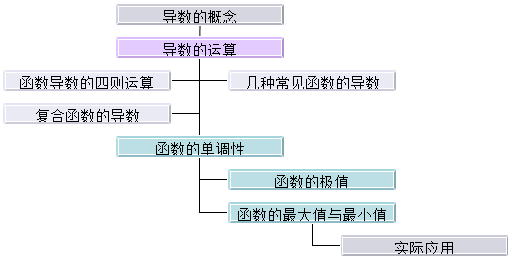
二．本章知识总结

（1）导数的概念：

1．导数的定义：对函数y=f(x)，在点x=x0处给自变量x以增量x，函数y相应有增量y=f(x0+x)－f(x0)，若极限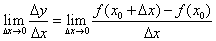存在，则此极限称为f(x)在点x=x0处的导数，记为f ’(x0)，或y’|；

2．导函数：如果函数y=f(x)在区间(a，b)内每一点都可导，就说y=f(x)在区间(a，b)内可导．即对于开区间(a，b)内每一个确定的x0值，都相对应着一个确定的导数f ’(x0)，这样在开区间(a，b)内构成一个新函数，把这一新函数叫做f(x)在(a，b)内的导函数．简称导数．记作f ’(x)或y’.

即f ’(x)=y’==。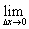

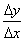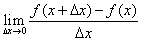3．导数的几何意义：函数y=f(x)在点x0处的导数的几何意义，就是曲线y=f(x)在P(x0，f(x0))处的切线的斜率，即曲线y=f(x)在点P(x0，f(x0))处的切线斜率为k＝f ’(x0)．函数 y＝f(x)在点 P(x0，f(x0))处的切线方程为 y－y0=f ’(x0)·(x－x0)．函数y=f(x)在点P(x0，f(x0))处的法线方程为y－y0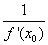＝－(x－x0)或x＝x0.

（2）常见函数的导数：

(c)’=0, (c为常数)；(xm)’=mx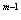；(sinx)’=cosx；

(cosx)’=－sinx；(ex)’=ex；(ax)’=ax·lna；(lnx)’=；(ligax)’=.

（3）导数的运算：

1．函数的和或差的导数

法则：两个函数的和或差的导数，等于两个函数的导数的和或差，即(u±v)’＝u’±v’.

2．函数的积的导教

  法则：两个函数的积的导数，等于第一个函数的导数乘以第二个函数，加上第一个函数乘以第二个函数的导数，即  (uv)’＝u’v+v’u.

3．函数的商的导

法则：两个函数的商的导数，等于分子的导数与分母的积，减去分母的导数与分子的积，再除以分母的平方．即(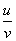)’= 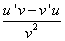(v≠0)。

4．复合函数的导数

法则：设函数u＝g(x)在点x处有导数u’x＝g’(x)，函数f(u)在点x处的u处有导数y’u=f ’(u)；则复合函数y=f[(x)]在点x处也有导数，且 y’x＝y’u·u’x，也可简述为：复合函数对自变量的导数，等于已知函数对中间变量的导数乘以中间变量对自变量的导数。

（4）函数的单调性

设函数y=f(x)在某个区间内可导，如果f ’( x)>0时，则函数y=f( x)为增函数；如果f ’(x)<0时，则函数y＝f(x)为减函数；如果恒有f ’( x)＝0，则y=f(x)为常函数.

（5）函数的极值

    1．设函数y=f(x)在x0附近有定义，如果对x0附近的所有点x都有f(x)＜f(x0)，则称f(x0)是函数f(x)的一个极大值，记作y极大值=f(x0)；

    2．如果对x0附近的所有点x，都有f(x)＞f(x0)称f(x0)是函数f(x)的一个极小值，记作y极小值=f(x0)，极大值与极小值统称为极值。

3．判断法则：

① 对于在x0处连续的函数，如果在x0附近的左侧f ’(x)>0，右侧f ’(x)<0，那么f(x0)是极大值；

② 如果在x0附近的左侧f ’(x)<0，右侧f ’(x)>0，那么f(x0)是极小值．

（6）函数的最大值与最小值

1．定义：最值是一个整体性概念，是指函数在给定区向(或定义域)内所有函数值中最大的值或最小的值，最大数值叫最大值，最小的值叫最小值，通常最大值记为M，最小值记为m.

2．存在性：在闭区间[a，b]上连续函数f(x)在[a，b]上必有最大值与最小值．

3．求最大（小）值的方法：函数f(x)在闭区间[a，b]上最值求法：

    ① 求出f(x)在(a，b)内的极值；

    ② 将函数f(x)的极值与f(a)，f(b)比较，其中较大的一个是最大值，较小的一个是最小值.

三．学习方法与指导

（一）学习方法点拨

1．导数的概念：

设f(x)在点x=x0 附近有定义，若极限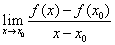存在，则称其为f(x)在点x=x0处的导数f ’(x0)．可以证明这一结论与教科书上的导数定义是等价的．

另外，若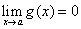，且存在a的邻域（α，β），当x∈(α, x0)∪(x0, β)时，有g(x)≠0，则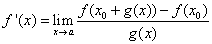，又若，且存在a的邻域(α，β)，当x∈(α, x0)∪(x0, β)时，有g(x)≠x0，则.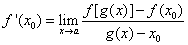

设f(x)=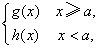 那么g(a)=h(a)=A，且

为f(x)在点x＝a处可导的充要条件，此时f ’(a)＝B．

由此可知，若分段函数f(x)的表达式中的g(x)、h(x)可分别看做含有a的区间(α，β)上的函数，且g(a)＝h(a)，g’(a)=h’(a)，则f(x)在点x=a处可导；且有f ’(a)=＝g’(a)＝h’(a)．

2．曲线的切线：

    设曲线S：y=f(x)，若f ’(x0)存在，则S在点P(x0，f(x0)处的切线方程为

    l：y－f(x0)＝f’(x0)(x－x0)．

    可见l的方程被x0所唯一确定；若f(x)在区间(α，β)内可导，则当点x0在(α，β)内变动时，点P(x0，f(x0))在S上变动，而l“贴着”曲线S转动．所以要求具有某种性质的切线，可转化为这种性质对点x0的要求，解出x0，即可求出对应的切线方程．

  应当了解可能一曲线在某点处不可导；但在这一点的切线还是存在的，例如曲线y=在点x＝0处不可导，但在原点处有切线x＝0．

3．导数运算

    要熟练掌握基本导数公式以及函数的和、差、积、商的求导法则．

    对复合函数求导法则，应首先搞清楚函数的复合过程，方法是研究运算顺序，例如给定函数y＝ln(sinex)，所谓运算顺序是指对自变量x，应先计算u=ex，再计算v=sinu，最后算出y＝lnv，然后倒过来即得复合过程y＝lnv，v=sinu，u＝ex，从而有y’=．

    对复合函数求导法则的掌握，要熟练到可以不写出复合过程而直接写出求导结果．

4．函数的单调性

    应当理解函数的单调性与可导性并无本质的联系，甚至具有单调性的函数并不一定连续．我们只是利用可导来研究单调性，这样就将研究的范围局限于可导函数．

    f(x)在区间I上可导，那么f ’(x)> 0是f(x)为增函数的充分条件，例如f(x)=x3是定义于R的增函数，但f ’(0)=0，这说明f ’(x)>0非必要条件．

    我们也可利用导数来证明一些不等式．如f(x)、g(x)均在[a、b]上连续，(a，b)上可导，那么令h(x)＝f(x)－g(x)，则h(x)也在[a，b]上连续，且在(a，b)上可导，若对任何x∈(a，b)有 h’(x)>0且 h(a)≥0，则当x∈(a，b)时 h(x)>h(a)=0，从而f(x)>g(x)对所有x∈(a，b)成立．

5．可导函数的极值

    从函数的极值定义看，极值的存在与可微性无必然联系．如f(x)=|x－1|，易见当x=1时f(x)取得极小值，但f ’(1)不存在．所以用研究导数的方法探求函数的极值，实际上是将研究的范围局限于可导函数．

    对可导函数f(x)，在x=x0取极值的必要条件是f(x0)＝0．又设f(x)在点x=x0处取得极小值，是否一定存在x0的邻域(α，β)，使当x∈(α，x0)时f ’(x)<0，且当x∈(x0，β)时f ’(x)>0，答案是否定的，即f ’(x)在x0的“左侧附近”为负，且在x0“右侧附近”为正仅是f(x0)为极小值的充分条件，为说明这一情况，我们考察函数f(x)=，由于,故有，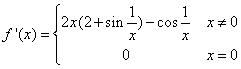

即f(x)在R上可导．又当x≠0时f(x)>0，而f(0)=0，故当x＝0时f(x)取得极小值0，但对任何α<0，总可取到充分小的 k∈Z，使 x1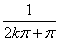＝∈(α，0)，且f ’(x1)=>0，又对任何β>0，总可取到充分大的k∈Z，使x2=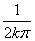∈(0，β)，且f ’(x2)=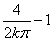<0．

6．函数的最大值与最小值

    函数的极值是“局部性质”，例如极小值点是指存在一个邻域，在其中此点的函数值最小，而函数的最大值、最小值是“全局性质”，即在函数的整体定义域内的某点处函数值最大（小），这两个概念是有区别的．但它们也有联系，即当最大（小）值点在区间内部时，它当然也是极值点，所以求定义于区间[a，b]上的函数f(x)的最大（小）值时，只需此较诸极值与区间端点处的函数值f(x)、f(b)即可．

    我们知道，[a，b]上的连续函数 f(x)必有最大值与最小值．若又有 f(x)在(a， b)上可导的条件，则由极值点处f ’(x)＝0可知最大（小）值点 x0∈{x| f ’(x0)=0或x＝a或x＝b}．但由于f(x)在[a，b]上连续并不能保证其在(a，b)内可导，而最大（小）值可能出现在f ’(x)不存在的点处（如f(x)=|x(x－1)|，易见最小值为0，出现在点x=0或x＝1处，而此时f ’(x)不存在），所以若仅有f(x)在[a，b]连续的条件，为求f(x)的最大（小）值，还需要求出使f ’(x)不存在的点，将这些点处的函数值与诸极值及f(a)、f(b)比较，从而确定最大值与最小值．

    根据上述分析，若f(x)在[a，b]上连续，在(a，b)内可导，如果我们可从另外的途径，比如问题的实际背景判断出f(x)的最小值不可能出现在点x＝a、x＝b处，那么当方程f ’(x)＝0在(a，b)内仅有一解x0时，则可断定f(x0)为最小值．