数列高考知识点归纳(非常全!)
数列高考知识点大扫描
数列基本概念
数列是一种特殊函数,对于数列这种特殊函数,着重讨论它的定义域、值域、增减性和最值等方面的性质,依据这些性质将数列分类:
依定义域分为:有穷数列、无穷数列;
依值域分为:有界数列和无界数列;
依增减性分为递增数列、递减数列和摆动数列。
数列的表示方法:列表法、图象法、解析法(通项公式法及递推关系法);
数列通项: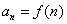

2、等差数列
1、定义 当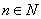 ,且
,且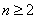 时,总有
时,总有 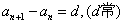 ,d叫公差。
,d叫公差。
2、通项公式 
1)、从函数角度看 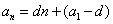 是n的一次函数,其图象是以点
是n的一次函数,其图象是以点 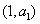 为端点, 斜率为d斜线上一些孤立点。
为端点, 斜率为d斜线上一些孤立点。
2)、从变形角度看 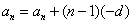 , 即可从两个不同方向认识同一数列,公差为相反数。
, 即可从两个不同方向认识同一数列,公差为相反数。
又 ,
,
相减得 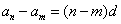 ,即
,即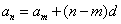 .
.
若 n>m,则以 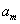 为第一项,
为第一项,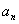 是第n-m+1项,公差为d;
是第n-m+1项,公差为d;
若n<m ,则 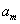 以为第一项时,
以为第一项时,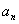 是第m-n+1项,公差为-d.
是第m-n+1项,公差为-d.
3)、从发展的角度看 若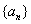 是等差数列,则
是等差数列,则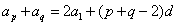 ,
,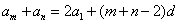 , 因此有如下命题:在等差数列中,若
, 因此有如下命题:在等差数列中,若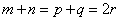 , 则
, 则 .
.
3、前n项和公式
由 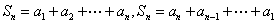 ,
,
相加得  , 还可表示为
, 还可表示为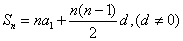 ,是n的二次函数。
,是n的二次函数。
特别的,由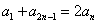 可得
可得 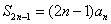 。
。
3、等比数列
1、 定义 当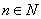 ,且
,且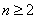 时,总有
时,总有  , q叫公比。
, q叫公比。
2、通项公式:  , 在等比数列中,若
, 在等比数列中,若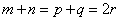 , 则
, 则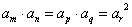 .
.
3、前n项和公式:
由  , 两式相减,
, 两式相减,
当 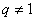 时,
时, ;当
;当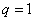 时 ,
时 ,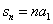 。
。
关于此公式可以从以下几方面认识:
①不能忽视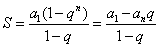 成立的条件:
成立的条件: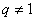 。特别是公比用字母表示时,要分类讨论。②公式推导过程中,所使用的“错位相消法”,可以用在相减后所得式子能够求和的情形。
。特别是公比用字母表示时,要分类讨论。②公式推导过程中,所使用的“错位相消法”,可以用在相减后所得式子能够求和的情形。
如,公差为d 的等差数列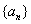 ,
,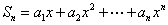 ,则
,则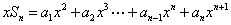 ,
,
相减得 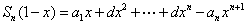 ,
,
当  时,
时,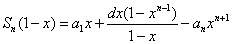 ,
,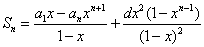
当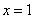 时 ,
时 ,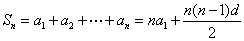 ;
;
3)从函数角度看 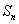 是n的函数,此时q和
是n的函数,此时q和 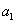 是常数。
是常数。
4、等差与等比数列概念及性质对照表

5、递推数列 表示数列中相邻的若干项之间关系的式子叫数列递推公式。作为特殊的函数,数列可用递推式表示。求递推数列通项公式常用方法:公式法、归纳法、累加法、累乘法。特别的,累加法是求形如 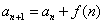 递推数列的基本方法,其中数列
递推数列的基本方法,其中数列 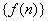 可求前n项和,即
可求前n项和,即 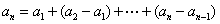 ;累乘法是求形如
;累乘法是求形如 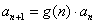 递推数列通项公式的基本方法,其中数列
递推数列通项公式的基本方法,其中数列 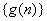 可求前n项积,即
可求前n项积,即 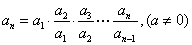 .
.
第一节 等差数列的概念、性质及前n项和
题根一 等差数列{an}中, ,求S20
,求S20
[思路]等差数列前n项和公式 :
:
1、 由已知直接求a1 ,公差d.
2、 利用性质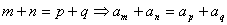
[解题 ] 由 ,
,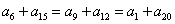 ,得
,得 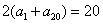 ,
,
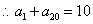 ,
, 。
。
[收获] 灵活应用通项性质可使运算过程简化。
[请你试试 1——1]
1、 等差数列{an} 满足 ,则有 ( )
,则有 ( )
A、 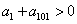 B、
B、 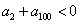 C、
C、 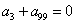 D、
D、 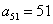
2、 等差数列中,a3+a7-a10=8,a11-a4=4,求 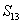 。
。
第1变 求和方法——倒序相加法
[变题1] 等差数列{an}共10项, ,
,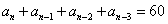 ,求Sn.
,求Sn.
[思路] 已知数列前四项和与后四项和,结合通项性质,联想Sn公式推导方法。
[解题] 已知 ,
,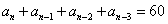 ,
,
又  ,得
,得 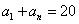 ,
,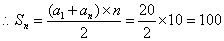 ,
,
[收获] 1、重视倒加法的应用,恰当运用通项性质: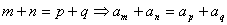 ,快捷准确;
,快捷准确;
3、 求出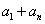 后运用“整体代换”手段巧妙解决问题。
后运用“整体代换”手段巧妙解决问题。
[请你试试 1——2]
1、 等差数列{an}共2k+1项,所有奇数项和为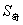 ,所有偶数项和为
,所有偶数项和为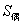 ,求
,求 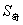 :
: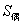 的值。
的值。
2、 等差数列{an}前n项和为18 ,若 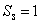 ,
, 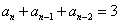 , 求项数n .
, 求项数n .
3、 求由 1,2,3,4四个数字组成的无重复数字的所有三位数的和。
4、 求和  。
。
第2变 已知前n项和及前m项和,如何求前n+m项和
[变题2] 在等差数列{an}中,Sn=a,Sm=b,(m>n),求Sn+m的值。
[思路] 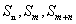 下标存在关系:m+n=m+n, 这与通项性质
下标存在关系:m+n=m+n, 这与通项性质 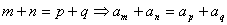 是否有关?
是否有关?
[解题] 由Sn=a,Sm=Sn+a n+1+an+2+……+am=b 得 a n+1+an+2+……+am =b-a,
即 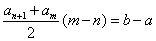 , 得
, 得 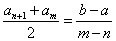
由(n+1)+m=1+(n+m), 得an+1+am=a1+am+n
故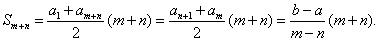
[请你试试 1——3]
1、在等差数列{an}中,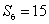 ,
,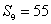 ,求
,求 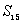 。
。
2、在等差数列{an}中,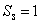 ,
, ,求
,求 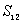 。
。
第3变 已知已知前n项和及前2n项和,如何求前3n项和
[变题3] 在等差数列{an}中,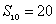 ,
,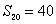 ,求
,求 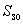
[思路] 由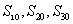 寻找
寻找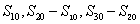 之间的关系。
之间的关系。
[解题] 设数列{an}公差为d ,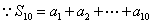 ,
,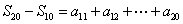 ,
,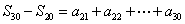 ,
, 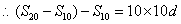 ,
,  ,
,
所以 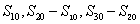 成等差数列,公差100d , 于是
成等差数列,公差100d , 于是 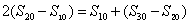 ,得
,得 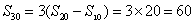 。
。
[收获] 1、在等差数列{an}中,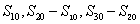 成等差数列,即
成等差数列,即 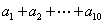 ,
,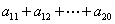 ,
,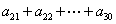 ,……,成等差数列,且
,……,成等差数列,且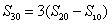 。
。
3、 可推广为 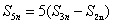 ,
,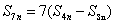 ,……,
,……,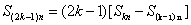 。
。
[请你试试 1——4]
1、在等差数列{an}中,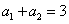 ,
,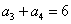 ,求
,求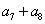
2、在等差数列{an}中,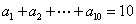 ,
,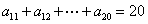 ,求
,求 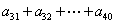
3、在等差数列{an}中,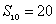 ,
,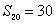 ,求
,求  及
及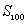 。
。
4、数列{an}中, ,
,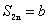 ,求
,求  。
。
5、等差数列{an}共有3k项,前2k项和 ,后2k项和
,后2k项和 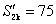 ,求中间k项和
,求中间k项和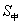 。
。
第4变迁移变换重视Sx=Ax2+Bx 的应用
[变题4] 在等差数列{an}中,Sn=m,,Sm=n,(m>n),求Sn+m的值。
[思路] 等差数列前n项和公式是关于n的二次函数,若所求问题与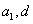 无关时,常设为S=An2+Bn形式。
无关时,常设为S=An2+Bn形式。
[解题] 由已知可设 Sn=An2+Bn=m Sm=Am2+Bm=n ,
两式相减 ,得 A(n+m)(n-m)+B(n-m)=m-n , 又m>n , 所以  ,
,
得 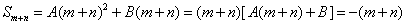 。
。
[收获] “整体代换”设而不求,可以使解题过程优化。
[请你试试 1——5]
1、 在等差数列{an}中,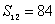 ,
,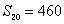 ,求
,求 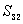
2、 在等差数列{an}中,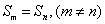 ,,求
,,求 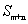
3、 在等差数列{an}中,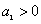 ,
, ,求 当n为何值时,
,求 当n为何值时, 有最大值
有最大值
第5变 归纳总结,发展提高
[题目] 在等差数列{an}中,Sn=a,Sm=b,(m>n),求Sn+m的值。(仍以变题2为例)
除上面利用通项性质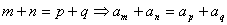 求法外,还有多种方法。现列举例如下:
求法外,还有多种方法。现列举例如下:
1、 基本量求解:
由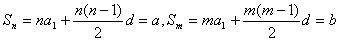 ,
,
相减得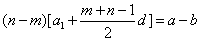 ,
, 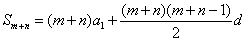
代入得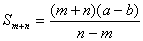 。
。
2、利用等差数列前x项和公式Sx=Ax2+Bx求解
由Sx=Ax2+Bx,得 Sn=An2+Bn, Sm=Am2+Bm
两式相减 ,得 A(n+m)(n-m)+B(n-m)=a-b
即 故
故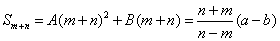
3、利用关系式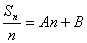 求解
求解
由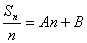 知
知 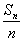 与n成线性关系,从而点集{(n,
与n成线性关系,从而点集{(n, 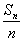 )}中的点共线,即(n,
)}中的点共线,即(n, 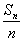 ),
),
(m, 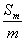 ),(m+n,
),(m+n, 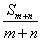 )共线,则有
)共线,则有 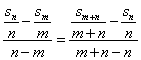 , 即
, 即 ,
,
化简, 得 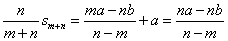 , 即
, 即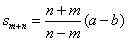 .
.
4、利用定比分点坐标公式求解
由A(n, 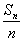 ), B(m,
), B(m, 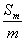 ), P(m+n,
), P(m+n, 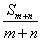 )三点共线,将点P看作有向线段
)三点共线,将点P看作有向线段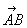 的定比分点,则
的定比分点,则 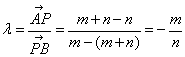 ,可得
,可得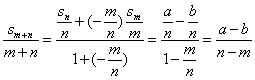 ,
,
即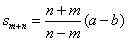 .
.
[请你试试 1——6]
若Sn是等差数列{an}的前n项和,S2=3,S6=4 ,则S12______.
第二节 等比数列的概念、性质及前n项和
题根二 等比数列{an} , 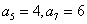 , 求
, 求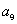 。
。
[思路] 1、由已知条件联立,求,从而得
2、由等比数列性质,知成等比数列。
[解题1] 由  , 两式相除,得
, 两式相除,得 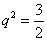 ,
,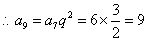 。
。
[解题2] 由 成等比,得
成等比,得 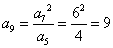 。
。
[收获] 1、灵活应用性质,是简便解题的基础;
2、等比数列中,序号成等差的项,成等比数列。
[ 请你试试2 ——1]
等比数列{an} , 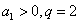 ,若
,若 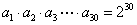 ,则
,则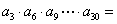 _______。
_______。
第1变 连续若干项之和构成的数列仍成等比数列
[变题2] 等比数列{an} ,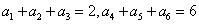 ,求
,求 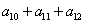 。
。
[思路] 等比数列中,连续若干项的和成等比数列。
[解题] 设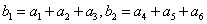 ,……,
,……, ,
,
则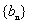 是等比数列,
是等比数列,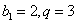 ,
,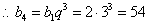 ,即
,即  。
。
[收获] 等比数列{an} , 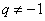 时,
时,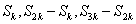 ,…… 成等比数列,但总有
,…… 成等比数列,但总有 。当k为偶数时,
。当k为偶数时,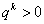 恒成立。
恒成立。
[请你试试2——2]
1、等比数列{an} , 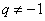 时,
时,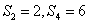 ,求
,求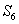 。
。
2、等比数列{an} , 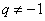 时,
时,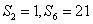 ,求
,求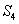 。
。
第2变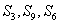 成等差,则
成等差,则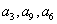 成等差
成等差
[变题3] 等比数列{an} 中, 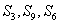 成等差,则
成等差,则 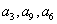 成等差 。
成等差 。
[思路] 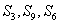 成等差,得
成等差,得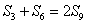 ,要证
,要证 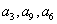 等差,只需证
等差,只需证  。
。
[解题]由 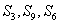 成等差,得
成等差,得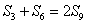 ,
,
当 q=1时,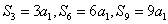 , 由
, 由  得
得 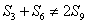 ,
,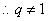 。
。
由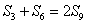 , 得
, 得 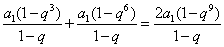 ,
,
整理得 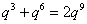 ,
,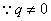 ,得
,得 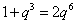 ,
,
两边同乘以 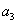 , 得
, 得  ,即
,即 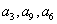 成等差。
成等差。
[收获] 1、等比数列{an} 中,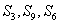 成等差,则
成等差,则  成等差。
成等差。
2、等比数列{an} 中,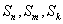 成等差,则
成等差,则 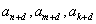 (其中
(其中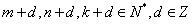 )成等差
)成等差
3、等比数列{an} 中,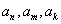 成等差,则
成等差,则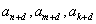 (其中
(其中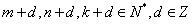 )成等差。
)成等差。
[请你试试2——3]
1、 等比数列{an} , 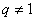 ,
,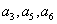 成等差, 求
成等差, 求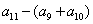 的值。
的值。
2、等比数列{an} ,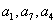 成等差,求证
成等差,求证  成等比。
成等比。
第3变 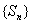 是等比,
是等比,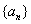 也是等比数列
也是等比数列
[变题4]数列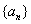 中,
中, 且
且 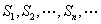 ,是等比数列,公比 q (
,是等比数列,公比 q (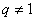 ),求证
),求证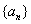 (
(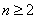 ) 也是等比数列。
) 也是等比数列。
[思路] 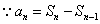 ,欲证
,欲证 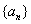 为等比数列,只需证
为等比数列,只需证  为常数。
为常数。
[解题] 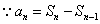 ,
, ,(
,(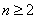 ), 得
), 得 ,而
,而 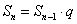 ,
,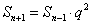 ,
,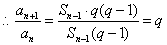 ,(
,(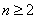 ), 故
), 故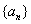 从第二项起,构成等比数列,公比为 q 。
从第二项起,构成等比数列,公比为 q 。
第4变 等比数列在分期付款问题中应用
问题 顾客购买一售价为5000元的商品时,采用分期付款方法,每期付款数相同,购买后1个月付款一次,到第12次付款后全部付清。如果月利润为0.8%,每月利息按复利计算,那么每期应付款多少?(精确到1元)
分析一:设每期应付款x元,则
第1次付款后,还欠 5000(1+0.8%)-x(元)
第2次付款后,还欠 [5000(1+0.8%)2-x(1+0.8%)-x=5000(1+0.8%)2-x(1+0.8%)-x(元)
第3次付款后,还欠 {5000(1+0.8%)2-x(1+0.8%)-x}(1+0.8%)-x=5000(1+0.8%)3-x(1+0.8%)2-x(1+0.8%)-x(元)
…………
最后一次付款后,款已全部还清,则 5000(1+0.8%)12-x(1+0.8%)11-x(1+0.8%)10-……-x(1+0.8%)-x=0 ,
移项 5000(1+0.8%)12=x(1+0.8%)11+x(1+0.8%)10+……+x(1+0.8%)+x , 即 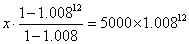
算得 
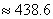 (元)
(元)
一般地,购买一件售价为a元的商品,采用分期付款时,要求在m个月内将款还至b元,月利润为p,分n(n是m的约数)次付款,那么每次付款数计算公式为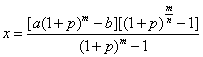 .
.
分析二:设每月还款x元,将商家的5000元折算成12个月后的钱要计算12个月的利息,而顾客第一次还的钱也应计算11个月的利息,第二次还的钱应计算10月的利息……,于是得方程
5000(1+0.8%)12=x(1+0.8%)11+x(1+0.8%)10+……+x(1+0.8%)+x, 解得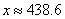 (元)
(元)
分析三:设每次还款x元,把还款折成现在的钱,可得
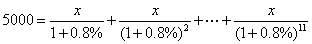 , 解得
, 解得 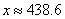 (元)。
(元)。
将上述方法应用到其他实际问题中,如木材砍伐,人口增长等。
[请你试试2——4]
某地现有居民住房的总面积为a m2,其中需要拆除的旧住房面积占了一半。当地有关部门决定在每年拆除一定数量旧住房的情况下,仍以10%的住房增长率建设新住房。如果10年后该地的住房总面积正好比目前翻一番,那么每年应拆除的旧住房总面积x是多少?(取1.110为2.6)
第三节 常见数列的通项及前n项和
[题根3] 求分数数列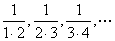 的前n项和
的前n项和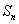
[思路] 写出数列通项公式,分析数列特点:分母中两因数之差为常数1。
[解题] 数列通项公式 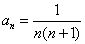 ,亦可表示为
,亦可表示为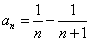 ,
,
所以 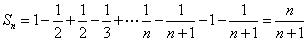 。
。
[收获] 将数列每一项裂为两项的差,再相加,使得正负抵消。
第1变 分母中两因数之差由常数1由到d
[变题1] 求分数数列 的前n项和
的前n项和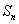 。
。
[思路] 写出通项公式,裂项求和。,
[解题] 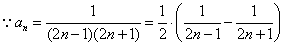 ,
,
 。
。
[收获]1、求分数数列的前n项和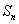 时,将数列每一项裂为两项的差,称裂项法。
时,将数列每一项裂为两项的差,称裂项法。
2、用裂项法可求解:
(1) 若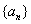 为等差数列,
为等差数列, ,公差为d,则
,公差为d,则
 .
.
3、常见裂项法求和有两种类型:分式型和根式型。如分式型 ;
;
根式型 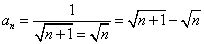 ;
;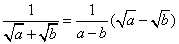 。另外还有:nn!=(n+1)!-n!,
。另外还有:nn!=(n+1)!-n!, 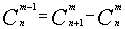 。
。
[请你试试 3——1]
1、求分数数列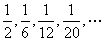 的前n项和
的前n项和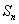
2、求分数数列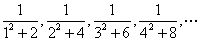 的前n项和
的前n项和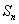 。
。
2、 求分数数列 的前n项和
的前n项和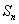 。
。
第2变分母中因数由2到3
[变题2] 求分数数列 的前n项和
的前n项和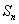 。
。
[思路] 数列中的项的变化:分母因数由两个变为三个,是否还可裂项呢?
[解题] 由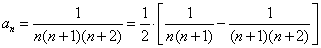 ,
,
得 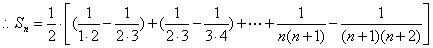
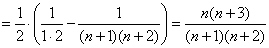 。
。
[收获] 1、分母为连续三因数的积,仍拆为两项的差,再相加,使得正负抵消。
2、对于公差为d (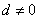 )的等差数列
)的等差数列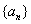 ,有
,有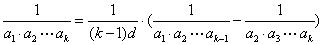 .
.
[请你试试 3——2]
1、求分数数列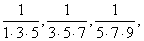 ……的前n项和
……的前n项和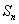 。
。
2、求分数数列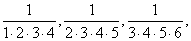 ……的前n项和
……的前n项和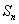 。
。
3、求分数数列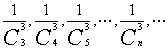 ……的前n项和
……的前n项和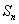 。
。
第3变 由分数数列到幂数列
[变题3] 求数列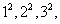 ……的前n项和
……的前n项和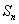 。
。
[思路] 利用恒等式 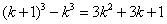 ,取k=1 , 2 , 3 ,……,相加正负抵消可解。
,取k=1 , 2 , 3 ,……,相加正负抵消可解。
[解题] 由恒等式 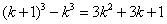
取k=1、2、3……, 得
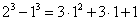
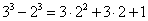
…………
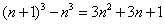
各式相加得 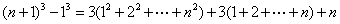
得 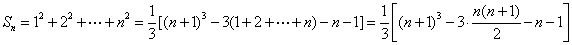
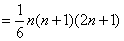 。
。
[收获] 利用恒等式 ,类似可得
,类似可得 
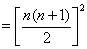 。
。
注意:正整数的平方和、立方和公式应用十分广泛。
[请你试试 3——3]
求和 (1)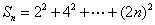 ,(2)
,(2)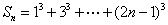 ,(3)
,(3)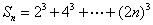 。
。
第4变 由幂数列到积数列
[变题4] 求数列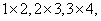 ……的前n项和
……的前n项和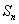 。
。
[思路1]写通项公式,由通项特征求解。
[解题1]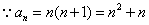 ,
,
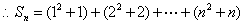
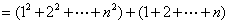
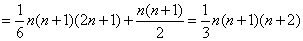 。
。
[思路2] 利用 裂项相加。
裂项相加。
[解题2] 由
得 
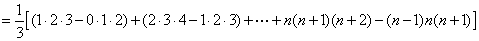
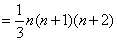 。
。
[收获] 对于通项为两因数的积,可推广到通项为k个因数的积,如求数列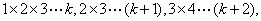 ……的前项和
……的前项和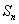 。
。
由 将每一项裂为两项的差,相加即可正负抵消。
将每一项裂为两项的差,相加即可正负抵消。
[思路3] 联想组合数公式,可见 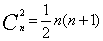 ,利用组合数性质可得。
,利用组合数性质可得。
[解题3] 由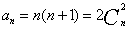 ,得
,得 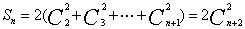
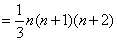 。
。
[请你试试 3——4]
求数列 ……的前n项和
……的前n项和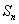 。
。
第4变 由等差数列与等比数列对应项的积构成的积数列
[变题5] 在数列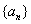 中,
中, ,(1) 分别求出
,(1) 分别求出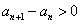 和
和 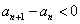 的n取值范围;(2)求数列最大项;(3)求数列前n项和
的n取值范围;(2)求数列最大项;(3)求数列前n项和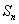 。
。
[思路] 1、解正整数不等式,2、利用函数单调性,3、利用错位相消法。
[解题] (1)由 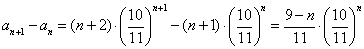 ,当n<9时,
,当n<9时,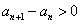 ,即
,即 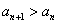 ;当 n<9时 ,
;当 n<9时 ,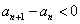 , 即
, 即  。
。
(2) 当n=9时,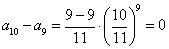 ,
, 是数列的最大项。
是数列的最大项。
(3) 设 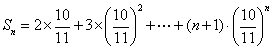 …………(1)
…………(1)
则 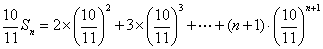 …………(2)
…………(2)
相减得 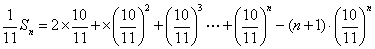
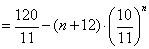 。
。
[请你试试 3——5]
1、 求数列  ……的前n项和
……的前n项和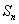 。
。
2、 求和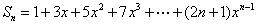 。
。
3、 求和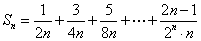 。
。
4、 已知数列 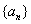 ,
,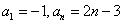 数列
数列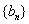 ,
,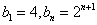 ,求数列
,求数列 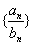 的前n项和
的前n项和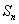 。
。
第四节 递推数列的通项公式及前n项和
1、利用不动点求数列通项
[题根三] 数列 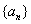 满足
满足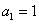 ,
,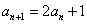 ,求通项公式
,求通项公式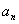 。
。
[思路] 1、写出 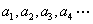 ,由不完全归纳法得
,由不完全归纳法得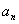 表达式。
表达式。
2、构造新数列,转化成等比数列求解。
[解题] 在的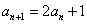 两边加1,则数列
两边加1,则数列 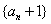 是首项为2,公比为2的等比数列,
是首项为2,公比为2的等比数列,
得  ,即
,即 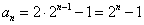 即为所求。
即为所求。
[收获] 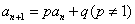 型递推数列,当p=1时, 数列为等差数列;当
型递推数列,当p=1时, 数列为等差数列;当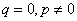 时,数列为等比数列。下面给出
时,数列为等比数列。下面给出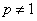 时递推式的通项公式的求法:
时递推式的通项公式的求法:
方法1、因为 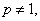 所以一定存在
所以一定存在 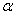 满足
满足 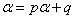 , 从而得
, 从而得 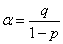 , 此为函数
, 此为函数 的不动点。 由
的不动点。 由 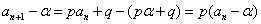 ,得
,得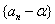 是首项为
是首项为  ,公比为p的等比数列,于是
,公比为p的等比数列,于是 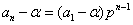 , 即
, 即 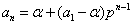 ,将
,将 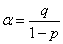 代入上式, 得 通项公式为
代入上式, 得 通项公式为 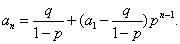 ………………(I)
………………(I)
方法2、由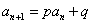 ,
,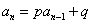 , 得
, 得 ,令
,令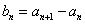 , 则
, 则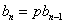 ,则
,则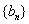 是首项为
是首项为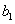 ,公比为q的等比数列, 得
,公比为q的等比数列, 得 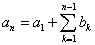
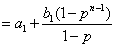
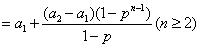 (*);当n=1时,(*)式也成立。
(*);当n=1时,(*)式也成立。
[请你试试4——1]
数列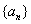 满足
满足 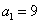 ,
, 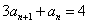 , 求
, 求 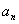 。
。
[变题1] 数列 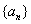 满足
满足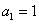 ,
,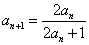 求通项公式
求通项公式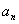 。
。
[思路] 常见解法:先求数列  的通项公式
的通项公式
[解题]由将已知关系式取倒数得 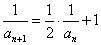 , 由(#)式 得
, 由(#)式 得 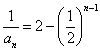 ,所以
,所以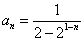 。
。
[收获]  型递推数列的通项公式的求法:
型递推数列的通项公式的求法:
令 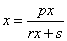 ,得
,得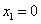 或
或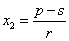 为两不动点。由于
为两不动点。由于 ,
,
设 ,则
,则 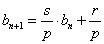 ,此为
,此为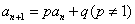 模型。 同样,
模型。 同样,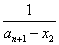 也可化为
也可化为 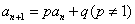 模型,由(I)式可求得
模型,由(I)式可求得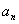 。更为特殊的是p=s 时,
。更为特殊的是p=s 时, , 设
, 设  则数列
则数列 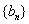 是等差数列 。我们常取
是等差数列 。我们常取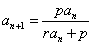 的倒数求解 ,原因恰是为此 。
的倒数求解 ,原因恰是为此 。
[变题2] (06年江西理第22题)数列 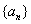 满足
满足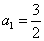 ,
,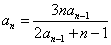
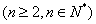 求通项公式
求通项公式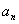 。
。
[解答] 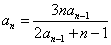
 ,即
,即
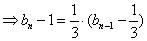 ,又
,又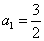 ,得
,得 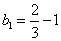 ,所以
,所以 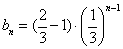 ,得
,得 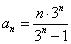 。
。
[请你试试4——2]
函数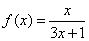 ,数列
,数列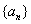 满足
满足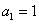 ,
,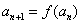 ,
,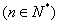 ,(1)求
,(1)求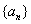 的通项公式
的通项公式 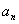 ;(2)设
;(2)设 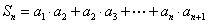 ,求
,求 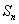 。
。
[变题2] 数列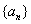 中,
中, ,求
,求 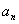
[思路1] 令 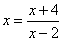 ,得
,得 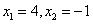 ,即两不动点,可得
,即两不动点,可得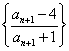 是等比数列,
是等比数列,
[解法1] 由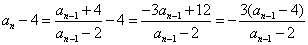 ,
,
令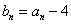 , 则
, 则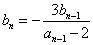 ……………………(a )
……………………(a )
由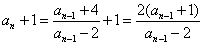 ,
,
令 , 则
, 则 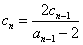 ……………………(b)
……………………(b)
(a) 式除以(b)式 得  ,即
,即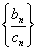 是首项为
是首项为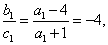
公比为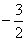 的等比数列,
的等比数列,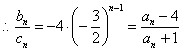 ,
,
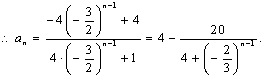
[思路2]  和
和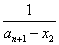 均可化为
均可化为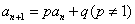 型递推式,
型递推式,
[解法2] 由 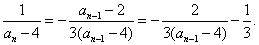
令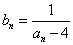 , 则
, 则 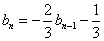 , 由(I)式 得
, 由(I)式 得

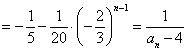
所以 
[解法3] 由 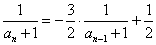 , 亦可求得
, 亦可求得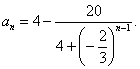
[收获] 求解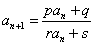 型递推数列的通项公式的方法:
型递推数列的通项公式的方法:
令 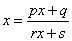 , 设其两根为
, 设其两根为  即两不动点。于是
即两不动点。于是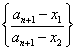 是等比数列, 并且
是等比数列, 并且 和
和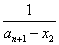 均可化为
均可化为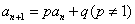 型递推式 。
型递推式 。
[请你试试4——3]
写出解法3的详细过程。
[变题3] 设数列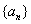 前n项和为
前n项和为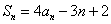 ,求
,求 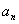 及
及 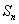 。
。
[思路] 将已知关系中 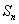 的化为
的化为 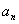 ,再进一步变形。
,再进一步变形。
[解题] 由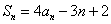 ,得
,得 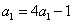 , 即
, 即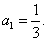
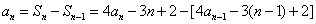
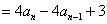 , 得
, 得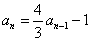 .
.
这是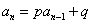 型递推式,由(#)式得
型递推式,由(#)式得
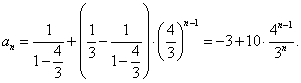
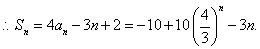
第1变递推式 
2、累积错位相消法求数列通项
[变题4] 数列 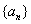 满足
满足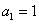 ,
,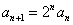 ,求通项公式
,求通项公式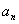 。
。
[思路] 观察 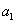 与
与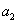 、
、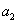 与
与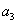 存在的关系,思考解题方法。
存在的关系,思考解题方法。
[解题] 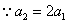 ,
, ,
,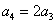 ,……,
,……,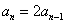 ,各式相乘得
,各式相乘得 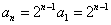 。
。
[收获] 1、若f(n)为常数, 则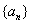 为等比数列。2、
为等比数列。2、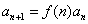 型递推式,通项公式求解方法如下:
型递推式,通项公式求解方法如下:
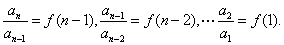
各式两边分别相乘,得 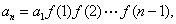 ……………………………(II)
……………………………(II)
当n=1时, (II)仍成立
[变题5] 在数列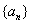 中,
中,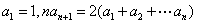 ,
,
(1) 求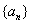 通项公式 (2)令
通项公式 (2)令 ,求
,求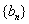 的前n项和
的前n项和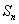 。
。
[思路] 将题中递推式转化、归类,再求解。
[解题] (1)将题中递推式转化为:
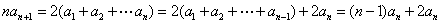 .
.
即 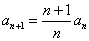 .由 (II) 式 得
.由 (II) 式 得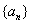 通项公式
通项公式
(2) 由 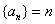 , 得
, 得 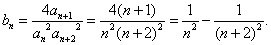
所以数列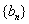 前n 项和 :
前n 项和 : 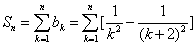
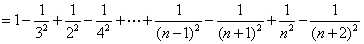

第2变 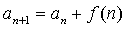 型递推数列
型递推数列
3、累加错位相消法求数列通项
[变题6] 已知数列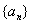 中,
中, ,
,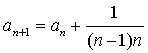 , 求
, 求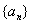 的通项公式。
的通项公式。
[思路] 将题中递推式变形  ,利用错位相消法。
,利用错位相消法。
解 将题中递推式表示为: ,
,
于是 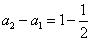 ,
,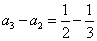 ,
,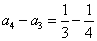 ,……,
,……,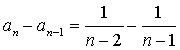
各式相加得 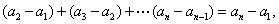
得 
 即为所求通项公式。
即为所求通项公式。
[收获] 对于数列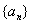 ,设
,设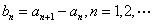 则称数列
则称数列 是
是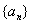 差数列, 则
差数列, 则
 得
得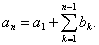
所以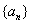 的通项公式为
的通项公式为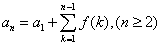 ………… (III). 当n=1时,也满足(III)式。
………… (III). 当n=1时,也满足(III)式。
[变题7] 在数列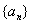 中,
中,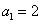 ,
, 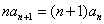 , 求
, 求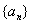 通项公式。
通项公式。
[思路] 题中关系式不是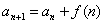 型的递推式,但两边同除以n(n+1),经过变量替换,可化为
型的递推式,但两边同除以n(n+1),经过变量替换,可化为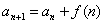 型递推式。
型递推式。
[解题] 在递推式 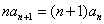 两边同除以 n(n+1) , 得
两边同除以 n(n+1) , 得 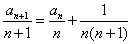
令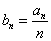 得
得 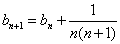 ,
, 。由(III)式得
。由(III)式得 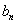 表达式为:
表达式为:
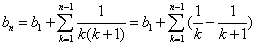
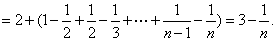
于是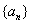 通项公式为
通项公式为 
[请你试试4——4]
求数列 1、4、11、26、57、120、……,的通项公式。
第3变 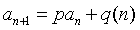 型递推数列
型递推数列
4、两边同除以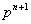 ,经过变量替换,化为
,经过变量替换,化为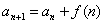 型递推式
型递推式
[变题8] 数列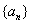 满足
满足 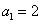 ,
, 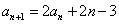 , 求
, 求 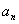 。
。
[思路] 递推式两边同除以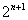 ,经过变量替换,可化为
,经过变量替换,可化为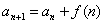 型递推式。
型递推式。
[解题] 在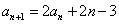 两边同除以
两边同除以 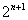 , 得
, 得 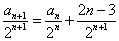
令  ,则
,则 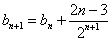 , 此为模型
, 此为模型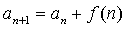 。
。
于是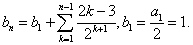 则
则
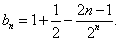
所以 
[收获] 在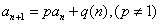 中,当q(n)是常数q时,即为模型
中,当q(n)是常数q时,即为模型 。
。
在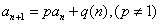 两边同除以
两边同除以 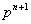 , 得
, 得 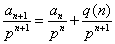 , 令
, 令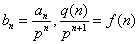 , 得
, 得 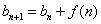 即可求出
即可求出 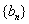 的通项公式,从而得
的通项公式,从而得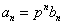 =
=

[变题9](20##年全国理第22题)设数列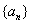 前n项和为
前n项和为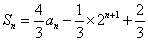 ,n=1,2,……,求通项
,n=1,2,……,求通项 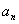 。
。
[解答] 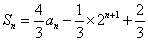
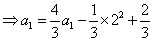
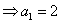 。因为
。因为 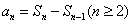 ,所以由题设得:
,所以由题设得:
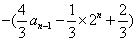
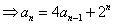
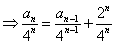 ,即
,即

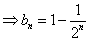 ,得
,得 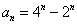 。
。
[规律小结] 根据数列性质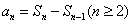 可得出递推关系,然后再根据结构特征求通项公式。
可得出递推关系,然后再根据结构特征求通项公式。
[请你试试4——5]
1、数列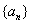 满足
满足  ,
, 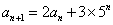 , 求
, 求 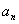 。
。
2、数列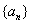 的前n项和
的前n项和 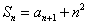 ,
,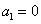 , 求
, 求 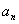
第3变 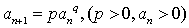 型
型
4、两边取对数,变形转化为模型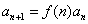
[变题10] 数列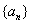 中
中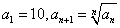 ,令
,令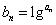 , (1)求数列
, (1)求数列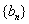 的通项公式,(2)设
的通项公式,(2)设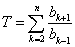 ,求
,求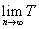 。
。
[思路] 利用对数运算法则变形转化。
解:(1)由已知得 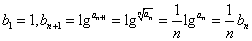 ,即模型
,即模型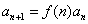 ,
,
由(II)式,得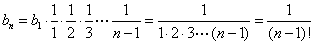 。
。
(2) 由 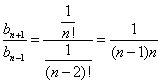 , 得
, 得 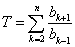
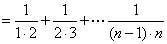
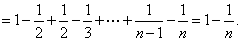 则
则  。
。
[收获] 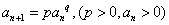 ,当q=1时,
,当q=1时,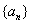 为等比数列。当
为等比数列。当 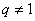 时,对递推式两边取常用对数,得
时,对递推式两边取常用对数,得 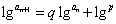 , 令
, 令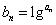 , 得
, 得 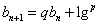 ,此为模型
,此为模型 ,即题根 。
,即题根 。
第4变 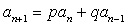 型
型
5、利用特征根求通项公式
[变题11] 在数列 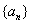 中,
中, 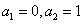 ,
,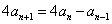 ,求
,求 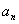
[思路] 在数列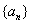 中,已知
中,已知 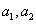 ,且
,且  ,求其通项公式方法介绍如下:当
,求其通项公式方法介绍如下:当  时,存在
时,存在 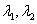 满足
满足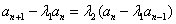 (*),即
(*),即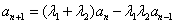 ,与
,与  比较系数,得
比较系数,得 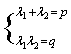 ,由根与系数的关系知
,由根与系数的关系知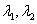 是二次方程
是二次方程 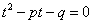 两实根,此方程称为递推式的特征方程。易见,只需将递推式中的
两实根,此方程称为递推式的特征方程。易见,只需将递推式中的 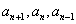
 换成
换成 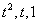 即可得特征方程。由 (*)式知数列
即可得特征方程。由 (*)式知数列 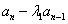 是等比数列,于是
是等比数列,于是 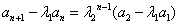 或
或 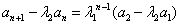 。当
。当 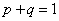 时,将p=1-q代入递推式,得
时,将p=1-q代入递推式,得 ,则
,则 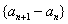 是以
是以 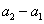 为首项,-q为公比的等比数列,从而
为首项,-q为公比的等比数列,从而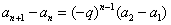 ,利用错位相消法即可求解。
,利用错位相消法即可求解。
[解题] 递推式特征方程为 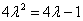 ,解得
,解得 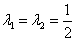 ,所以递推式可表示为
,所以递推式可表示为 ,数列
,数列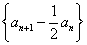 是首项为
是首项为 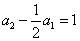 ,公比为
,公比为 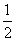 的等比数列,所以
的等比数列,所以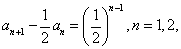 ……,两边同除以
……,两边同除以 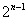 ,得
,得 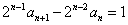 ,
,
于是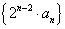 是首项为0,公差为1等差数列,故
是首项为0,公差为1等差数列,故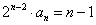 ,
,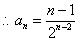 。
。
[收获] 一般的,在数列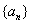 中,已知
中,已知 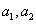 ,且
,且  ,它的特征方程
,它的特征方程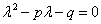 两根为
两根为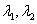 ,则,当
,则,当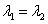 时 ,通项公式
时 ,通项公式 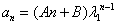 ;当
;当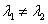 时 ,通项公式
时 ,通项公式 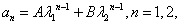 ……,其中A,B为常数,可由
……,其中A,B为常数,可由 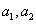 推出。
推出。
利用这一结论可方便的推出通项公式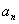 。
。
[变题12] 在数列 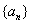 中,
中,  ,
,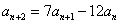 ,求
,求 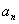
解:特征方程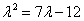 两根为
两根为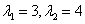 。设
。设 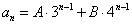 ,由
,由 ,得 A=2,B=-1, 故
,得 A=2,B=-1, 故 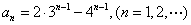 。
。
[请你试试 4——6]
1、在数列 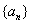 中,
中, 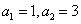 ,
,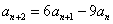 ,求
,求 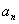 。
。
2、在数列 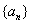 中,
中,  ,
,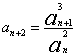 ,求
,求 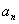 。
。
第六章 数列请你试试 答案与提示
[请你试试 1—1]:1、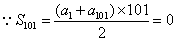 ,
, ,选 C
,选 C
2、a3+a7-a10+a11-a4=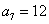 ,得
,得 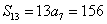 。
。
[请你试试 1—2]:1、略; 2、n=27; 3、由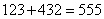 ,
, ;
;
4、倒加法 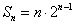 。
。
[请你试试 1—3]:1、200; 2、4 。
[请你试试 1—4]:1、12; 2、40; 3、 0、110; 4、3 (b-a);5、
 。
。
[请你试试 1—5]:1、 1504;2、0;3、12或13。
[请你试试 1—6]: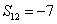 。
。
[请你试试2—1]:等比数列中某些项的积的问题,利用性质解。 设 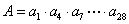 ,
, 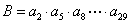 ,
,  ,易见A,B,C成等比,公比为
,易见A,B,C成等比,公比为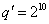 。 由
。 由 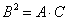 且
且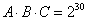 ,得
,得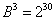 ,即
,即 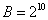 ,
,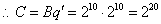 。
。
[请你试试2—2]:1、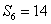 ;2、
;2、  或
或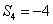 (舍去)。
(舍去)。
[请你试试2—3]:1、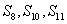 等差,则
等差,则 ,得
,得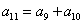 ,即
,即 =0;
=0;
2、略。
[请你试试2—4]:由上例分析得 a(1+10%)10-x(1+10%)9-……-x(1+10%)-x=2a,即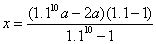 ,
,
即 2.6a-16x=2a  。
。
[请你试试3—1]:1、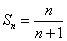 ;2、
;2、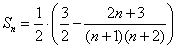 ;3、
;3、 。
。
[请你试试3—2]:1、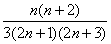 ;2、
;2、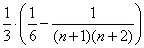 ;
;
3、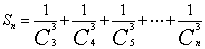
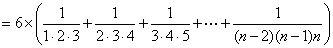
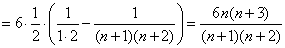 。
。
[请你试试3—3]:1、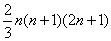 ;2、
;2、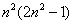 ;3、
;3、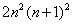 。
。
[请你试试3—4]: 。
。
[请你试试3—5]:1、 ;2、分
;2、分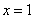 和
和  两种情形;3、
两种情形;3、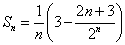 ;
;
4、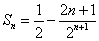 。
。
[请你试试4—1]:由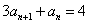 得
得  ,可得
,可得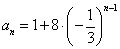 ;
;
或由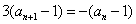 求。
求。
[请你试试4—2]:提示: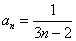 ;
; 。
。
[请你试试4—3]:略
[请你试试4—4]:由原数列得一阶差数列 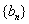 :3、7、15、31、63、……;由
:3、7、15、31、63、……;由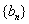 得 二阶差数列
得 二阶差数列 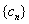 :
:
4、8、16、32、……,易得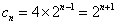 ,得
,得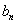 ,最后得原数列通项公式
,最后得原数列通项公式 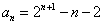 。
。
[请你试试4—5]:1、两边同除以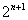 ,得
,得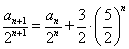 ,即
,即 ,得
,得 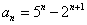 。2、由
。2、由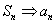 , 得
, 得 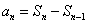
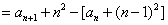
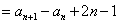 ,
,  。
。
[请你试试4—6]:1、特征方程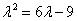 两根为
两根为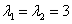 ,设
,设 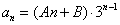 ,由
,由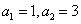 ,得 A=0,B=1, 故
,得 A=0,B=1, 故 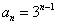 。2、取对数,
。2、取对数,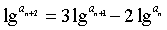 ,令
,令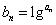 ,则
,则 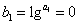 ,
,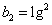 ,且
,且 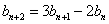 , ……,
, ……,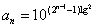 。
。
-
高考数学公式及知识点总结
高考前数学知识点总结集合与简易逻辑1对于集合一定要抓住集合的代表元素及元素的确定性互异性无序性如集合AxylgxByylgxCxy…
-
高中数学人教版必修2知识点总结
高中数学必修2知识点一直线与方程1直线的倾斜角定义x轴正向与直线向上方向之间所成的角叫直线的倾斜角特别地当直线与x轴平行或重合时我…
-
高中数学选修1-1知识点归纳
高中数学选修11知识点总结第一章简单逻辑用语1命题用语言符号或式子表达的可以判断真假的陈述句真命题判断为真的语句假命题判断为假的语…
-
高一数学知识点总结--必修5
高中数学必修5知识点第一章:解三角形1、正弦定理:在???C中,a、b、c分别为角?、?、C的对边,R为???C的外接圆的半径,则…
-
高中数学选修4-4知识点归纳
高中数学选修44知识点总结一选考内容坐标系与参数方程高考考试大纲要求1坐标系理解坐标系的作用了解在平面直角坐标系伸缩变换作用下平面…
-
高中数学数列知识点总结(经典)
数列基础知识点和方法归纳1.等差数列的定义与性质定义:an?1?an?d(d为常数),an?a1??n?1?d等差中项:x,A,y…
-
高中数列知识点总结
数列知识点总结第一部分等差数列一定义式:an?an?1?d二通项公式:an???am?(n?m)d?a?(n?1)d?1一个数列是…
-
20xx年高考数学数列知识点大总结
20xx年高考数学数列知识点及题型大总结等差数列知识要点1.递推关系与通项公式递推关系:an?1?an?d通项公式:an?a1?(…
-
高中数学数列知识点总结(经典)
1.等差数列的定义与性质定义:an?1?an?d(d为常数),an?a1??n?1?d等差中项:x,A,y成等差数列?2A?x?y…
-
最新高中数列知识点总结
数列知识点总结第一部分等差数列一定义式:an?an?1?d二通项公式:an???am?(n?m)d?a?(n?1)d?1一个数列是…
-
解三角形数列知识点总结
必修5第一章《解三角形》知识点归纳1.高线定理:△ABC中,a边上的高ha?bsinC?csinB2.正弦定理:△ABC中,asi…