空间向量与立体几何知识点归纳总结
空间向量与立体几何知识点归纳总结
一.知识要点。
1. 空间向量的概念:在空间,我们把具有大小和方向的量叫做向量。
注:(1)向量一般用有向线段表示 同向等长的有向线段表示同一或相等的向量。
同向等长的有向线段表示同一或相等的向量。
(2)向量具有平移不变性
2. 空间向量的运算。
定义:与平面向量运算一样,空间向量的加法、减法与数乘运算如下(如图)。

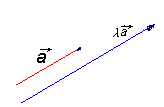
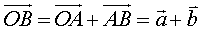 ;
;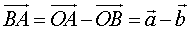 ;
;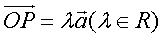
运算律:⑴加法交换律: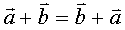
⑵加法结合律: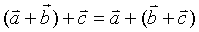
⑶数乘分配律: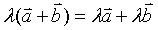
运算法则:三角形法则、平行四边形法则、平行六面体法则
3. 共线向量。
(1)如果表示空间向量的有向线段所在的直线平行或重合,那么这些向量也叫做共线向量或平行向量,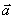 平行于
平行于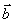 ,记作
,记作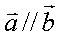 。
。
(2)共线向量定理:空间任意两个向量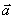 、
、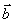 (
(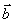 ≠
≠ ),
),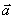 //
//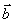 存在实数λ,使
存在实数λ,使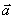 =λ
=λ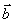 。
。
(3)三点共线:A、B、C三点共线<=>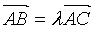
<=>
(4)与 共线的单位向量为
共线的单位向量为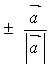
4. 共面向量
(1)定义:一般地,能平移到同一平面内的向量叫做共面向量。
说明:空间任意的两向量都是共面的。
(2)共面向量定理:如果两个向量 不共线,
不共线,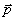 与向量
与向量 共面的条件是存在实数
共面的条件是存在实数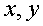 使
使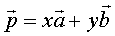 。
。
(3)四点共面:若A、B、C、P四点共面<=>
<=>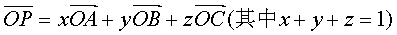
5. 空间向量基本定理:如果三个向量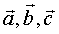 不共面,那么对空间任一向量
不共面,那么对空间任一向量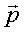 ,存在一个唯一的有序实数组
,存在一个唯一的有序实数组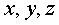 ,使
,使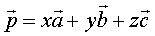 。
。
若三向量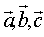 不共面,我们把
不共面,我们把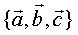 叫做空间的一个基底,
叫做空间的一个基底,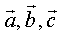 叫做基向量,空间任意三个不共面的向量都可以构成空间的一个基底。
叫做基向量,空间任意三个不共面的向量都可以构成空间的一个基底。
推论:设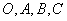 是不共面的四点,则对空间任一点
是不共面的四点,则对空间任一点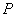 ,都存在唯一的三个有序实数
,都存在唯一的三个有序实数 ,使
,使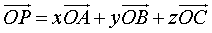 。
。
6. 空间向量的直角坐标系:
(1)空间直角坐标系中的坐标:
在空间直角坐标系 中,对空间任一点
中,对空间任一点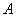 ,存在唯一的有序实数组
,存在唯一的有序实数组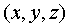 ,使
,使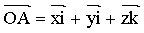 ,有序实数组
,有序实数组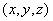 叫作向量
叫作向量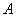 在空间直角坐标系
在空间直角坐标系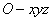 中的坐标,记作
中的坐标,记作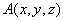 ,
,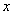 叫横坐标,
叫横坐标,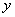 叫纵坐标,
叫纵坐标,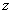 叫竖坐标。
叫竖坐标。
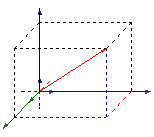
注:①点A(x,y,z)关于x轴的的对称点为(x,-y,-z),关于xoy平面的对称点为(x,y,-z).即点关于什么轴/平面对称,什么坐标不变,其余的分坐标均相反。②在y轴上的点设为(0,y,0),在平面yOz中的点设为(0,y,z)
(2)若空间的一个基底的三个基向量互相垂直,且长为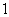 ,这个基底叫单位正交基底,用
,这个基底叫单位正交基底,用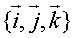 表示。空间中任一向量
表示。空间中任一向量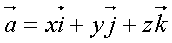 =(x,y,z)
=(x,y,z)
(3)空间向量的直角坐标运算律:
①若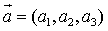 ,
, ,则
,则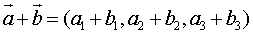 ,
,
 ,
,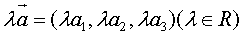 ,
,
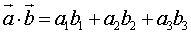 ,
,
 ,
,
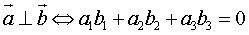 。
。
②若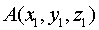 ,
, ,则
,则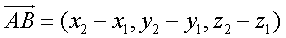 。
。
一个向量在直角坐标系中的坐标等于表示这个向量的有向线段的终点的坐标减去起点的坐标。
③定比分点公式:若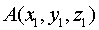 ,
, ,
,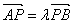 ,则点P坐标为
,则点P坐标为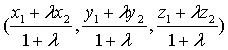 。推导:设P(x,y,z)则
。推导:设P(x,y,z)则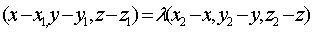 ,显然,当P为AB中点时,
,显然,当P为AB中点时,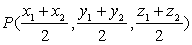
④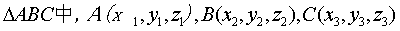 ,三角形重心P坐标为
,三角形重心P坐标为
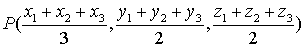
 ⑤ΔABC的五心:
⑤ΔABC的五心:
内心P:内切圆的圆心,角平分线的交点。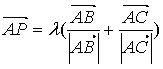 (单位向量)
(单位向量)
外心P:外接圆的圆心,中垂线的交点。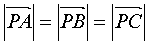
垂心P:高的交点: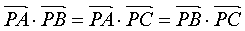 (移项,内积为0,则垂直)
(移项,内积为0,则垂直)
重心P:中线的交点,三等分点(中位线比)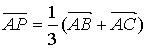
中心:正三角形的所有心的合一。
(4)模长公式:若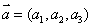 ,
,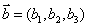 ,
,
则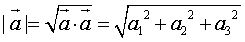 ,
,
(5)夹角公式: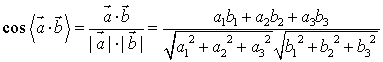 。
。
ΔABC中① <=>A为锐角②
<=>A为锐角②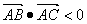 <=>A为钝角,钝角Δ
<=>A为钝角,钝角Δ
(6)两点间的距离公式:若 ,
,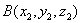 ,
,
则 ,
,
或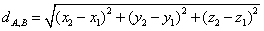
7. 空间向量的数量积。
(1)空间向量的夹角及其表示:已知两非零向量 ,在空间任取一点
,在空间任取一点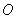 ,作
,作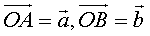 ,则
,则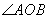 叫做向量
叫做向量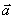 与
与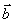 的夹角,记作
的夹角,记作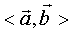 ;且规定
;且规定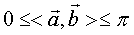 ,显然有
,显然有 ;若
;若 ,则称
,则称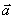 与
与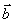 互相垂直,记作:
互相垂直,记作: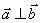 。
。
(2)向量的模:设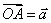 ,则有向线段
,则有向线段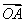 的长度叫做向量
的长度叫做向量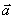 的长度或模,记作:
的长度或模,记作: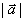 。
。
(3)向量的数量积:已知向量 ,则
,则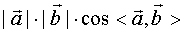 叫做
叫做 的数量积,记作
的数量积,记作 ,即
,即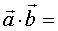
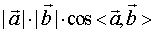 。
。
(4)空间向量数量积的性质:
① 。②
。②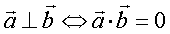 。③
。③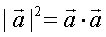 。
。
(5)空间向量数量积运算律:
①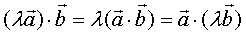 。②
。②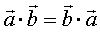 (交换律)。
(交换律)。
③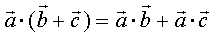 (分配律)。
(分配律)。
④不满足乘法结合率: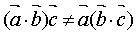
二.空间向量与立体几何
1.线线平行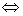 两线的方向向量平行
两线的方向向量平行
1-1线面平行 线的方向向量与面的法向量垂直
线的方向向量与面的法向量垂直
1-2面面平行 两面的法向量平行
两面的法向量平行
2线线垂直(共面与异面) 两线的方向向量垂直
两线的方向向量垂直
2-1线面垂直 线与面的法向量平行
线与面的法向量平行
2-2面面垂直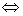 两面的法向量垂直
两面的法向量垂直
3线线夹角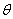 (共面与异面)
(共面与异面)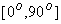
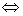 两线的方向向量
两线的方向向量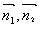 的夹角或夹角的补角,
的夹角或夹角的补角,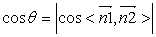
3-1线面夹角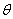
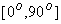 :求线面夹角的步骤:先求线的方向向量
:求线面夹角的步骤:先求线的方向向量 与面的法向量
与面的法向量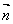 的夹角,若为锐角角即可,若为钝角,则取其补角;再求其余角,即是线面的夹角.
的夹角,若为锐角角即可,若为钝角,则取其补角;再求其余角,即是线面的夹角.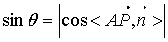
3-2面面夹角(二面角)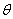
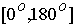 :若两面的法向量一进一出,则二面角等于两法向量
:若两面的法向量一进一出,则二面角等于两法向量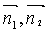 的夹角;法向量同进同出,则二面角等于法向量的夹角的补角.
的夹角;法向量同进同出,则二面角等于法向量的夹角的补角. 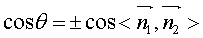
4.点面距离 :求点
:求点 到平面
到平面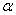 的距离: 在平面
的距离: 在平面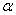 上去一点
上去一点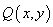 ,得向量
,得向量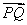 ;; 计算平面
;; 计算平面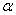 的法向量
的法向量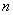 ;.
;.
4-1线面距离(线面平行):转化为点面距离
4-2面面距离(面面平行):转化为点面距离
第二篇:空间向量与立体几何知识点学生
用空间向量判断空间中的位置关系的常用方法
(1)线线平行
证明两条直线平行,只需证明两条直线的方向向量是共线向量.
(2)线线垂直
证明两条直线垂直,只需证明两条直线的方向向量垂直,即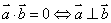 .
.
(3)线面平行
用向量证明线面平行的方法主要有:
①证明直线的方向向量与平面的法向量垂直;
②证明可在平面内找到一个向量与直线方向向量是共线向量;
③利用共面向量定理,即证明可在平面内找到两不共线向量来线性表示直线的方向向量.
(4)线面垂直
用向量证明线面垂直的方法主要有:
①证明直线方向向量与平面法向量平行;
②利用线面垂直的判定定理转化为线线垂直问题.
(5)面面平行
①证明两个平面的法向量平行(即是共线向量);
②转化为线面平行、线线平行问题.
(6)面面垂直
①证明两个平面的法向量互相垂直;
②转化为线面垂直、线线垂直问题.
6、运用空间向量求空间角
(1)求两异面直线所成角
利用公式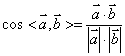 ,
,
但务必注意两异面直线所成角θ的范围是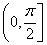 ,
,
故实质上应有: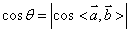 .
.
(2)求线面角
求直线与平面所成角时,一种方法是先求出直线及射影直线的方向向量,通过数量积求出直线与平面所成角;另一种方法是借助平面的法向量,先求出直线方向向量与平面法向量的夹角φ,即可求出直线与平面所成的角θ,其关系是sinθ=| cosφ|.
(3)求二面角
用向量法求二面角也有两种方法:一种方法是利用平面角的定义,在两个面内先求出与棱垂直的两条直线对应的方向向量,然后求出这两个方向向量的夹角,由此可求出二面角的大小;另一种方法是转化为求二面角的两个面的法向量的夹角,它与二面角的大小相等或互补.
7、运用空间向量求空间距离
空间中的各种距离一般都可以转化为求点与点、点与线、点与面的距离.
(1)点与点的距离
点与点之间的距离就是这两点间线段的长度,因此也就是这两点对应向量的模.
(2)点与面的距离
点面距离的求解步骤是:
①求出该平面的一个法向量;
②求出从该点出发的平面的任一条斜线段对应的向量;
③求出法向量与斜线段向量的数量积的绝对值再除以法向量的模,即得要求的点面距离.
直线的方向向量、平面的法向量及其应用
一、直线的方向向量及其应用
1、直线的方向向量
直线的方向向量就是指和这条直线所对应向量平行(或共线)的向量,显然一条直线的方向向量可以有无数个.
2、直线方向向量的应用
利用直线的方向向量,可以确定空间中的直线和平面.
(1)若有直线l, 点A是直线l上一点,向量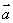 是l的方向向量,在直线l上取
是l的方向向量,在直线l上取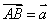 ,则对于直线l上任意一点P,一定存在实数t,使得
,则对于直线l上任意一点P,一定存在实数t,使得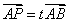 ,这样,点A和向量
,这样,点A和向量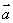 不仅可以确定l的位置,还可具体表示出l上的任意点.
不仅可以确定l的位置,还可具体表示出l上的任意点.
(2)空间中平面α的位置可以由α上两条相交直线确定,若设这两条直线交于点O,它们的方向向量分别是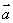 和
和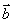 ,P为平面α上任意一点,由平面向量基本定理可知,存在有序实数对(x,y),使得
,P为平面α上任意一点,由平面向量基本定理可知,存在有序实数对(x,y),使得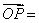
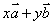 ,这样,点O与方向向量
,这样,点O与方向向量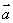 、
、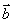 不仅可以确定平面α的位置,还可以具体表示出α上的任意点.
不仅可以确定平面α的位置,还可以具体表示出α上的任意点.
二、平面的法向量
1、所谓平面的法向量,就是指所在的直线与平面垂直的向量,显然一个平面的法向量也有无数个,它们是共线向量.
2、在空间中,给定一个点A和一个向量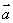 ,那么以向量
,那么以向量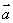 为法向量且经过点A的平面是唯一确定的.
为法向量且经过点A的平面是唯一确定的.
三、直线方向向量与平面法向量在确定直线、平面位置关系中的应用
1、若两直线l1、l2的方向向量分别是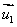 、
、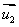 ,则有l1// l2
,则有l1// l2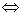
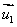 //
//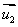 ,l1⊥l2
,l1⊥l2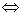
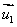 ⊥
⊥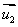 .
.
2、若两平面α、β的法向量分别是 、
、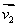 ,则有α//β
,则有α//β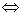
 //
//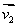 ,α⊥β
,α⊥β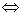
 ⊥
⊥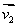 .
.
若直线l的方向向量是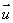 ,平面的法向量是
,平面的法向量是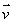 ,则有l//α
,则有l//α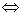
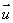 ⊥
⊥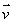 ,l⊥α
,l⊥α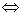
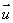 //
//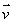
四、平面法向量的求法
若要求出一个平面的法向量的坐标,一般要建立空间直角坐标系,然后用待定系数法求解,一般步骤如下:
1、设出平面的法向量为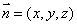 .
.
2、找出(求出)平面内的两个不共线的向量的坐标
3、根据法向量的定义建立关于x,y,z的方程组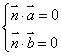
4、解方程组,取其中一个解,即得法向量
五、用向量方法证明空间中的平行关系和垂直关系
(一)用向量方法证明空间中的平行关系
空间中的平行关系主要是指:线线平行、线面平行、面面平行.
1、线线平行
设直线l1、l2的方向向量分别是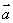 、
、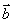 ,则要证明l1// l2,只需证明
,则要证明l1// l2,只需证明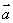 //
//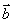 ,即
,即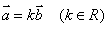
2、线面平行
(1)设直线l的方向向量是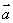 ,平面
,平面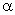 的法向量是
的法向量是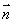 ,则要证明
,则要证明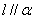 ,只需证明
,只需证明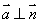 ,即
,即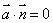 .
.
(2)根据线面平行的判定定理:“如果直线(平面外)与平面内的一条直线平行,那么这条直线和这个平面平行”,要证明一条直线和一个平面平行,也可以在平面内找一个向量与已知直线的方向向量是共线向量即可.
(3)根据共面向量定理可知,如果一个向量和两个不共线的向量是共面向量,那么这个向量与这两个不共线向量确定的平面必定平行,因此要证明一条直线和一个平面平行,只要证明这条直线的方向向量能够用平面内两个不共线向量线性表示即可.
3、面面平行
(1)由面面平行的判定定理,要证明面面平行,只要转化为相应的线面平行、线线平行即可.
(2)若能求出平面α、β的法向量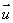 、
、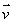 ,则要证明α//β,只需证明
,则要证明α//β,只需证明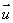 //
// 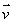
(二)用向量方法证明空间中的垂直关系
空间中的垂直关系主要是指:线线垂直、线面垂直、面面垂直.
1、线线垂直
设直线l1、l2的方向向量分别是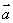 、
、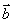 ,则要证明l1⊥ l2,只需证明
,则要证明l1⊥ l2,只需证明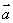 ⊥
⊥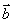 ,即
,即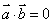
2、线面垂直
(1)设直线l的方向向量是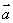 ,平面α的法向量是
,平面α的法向量是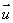 ,则要证l⊥α,只需证明
,则要证l⊥α,只需证明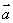 //
// 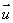
(2)根据线面垂直的判定定理,转化为直线与平面内的两条相交直线垂直.
3、面面垂直
(1)根据面面垂直的判定定理转化为证相应的线面垂直、线线垂直.
(2)证明两个平面的法向量互相垂直.
六、用向量方法求空间的角
(一)两条异面直线所成的角
1、定义:设a、b是两条异面直线,过空间任一点O作直线 ,则
,则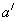 与
与 所夹的锐角或直角叫做a与b所成的角.
所夹的锐角或直角叫做a与b所成的角.
2、范围:两异面直线所成角θ的取值范围是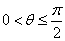
3、向量求法:设直线a、b的方向向量为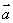 、
、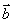 ,其夹角为
,其夹角为 ,则有
,则有
4、注意:两异面直线所成的角可以通过这两条直线的方向向量的夹角来求得,但两者不完全相等,当两方向向量的夹角是钝角时,应取其补角作为两异面直线所成的角.
(二)直线与平面所成的角
1、定义:直线和平面所成的角,是指直线与它在这个平面内的射影所成的角.
2、范围:直线和平面所成角θ的取值范围是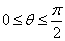
3、向量求法:设直线l的方向向量为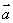 ,平面的法向量为
,平面的法向量为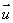 ,直线与平面所成的角为θ,
,直线与平面所成的角为θ,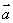 与
与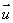 的夹角为
的夹角为 ,则有
,则有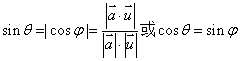
(三)二面角
1、二面角的取值范围: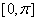
2、二面角的向量求法
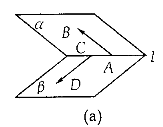
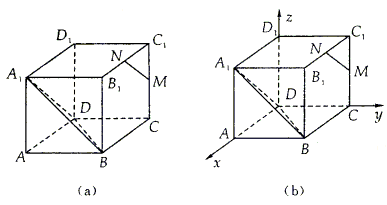
(1)若AB、CD分别是二面角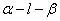 的两个面内与棱l垂直的异面直线,则二面角的大小就是向量
的两个面内与棱l垂直的异面直线,则二面角的大小就是向量 与
与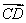 的夹角(如图(a)所示).
的夹角(如图(a)所示).
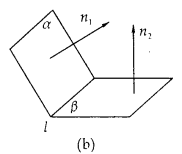
(2)设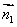 、
、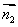 是二面角
是二面角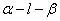 的两个角α、β的法向量,则向量
的两个角α、β的法向量,则向量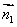 与
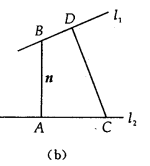
与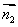 的夹角(或其补角)就是二面角的平面角的大小(如图(b)所示).
的夹角(或其补角)就是二面角的平面角的大小(如图(b)所示).
七、用向量的方法求空间的距离
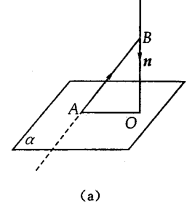
(一)点面距离的求法
如图(a)所示,BO⊥平面α,垂足为O,则点B到平面α的距离就是线段BO的长度.若AB是平面α的任一条斜线段,则在Rt△BOA中,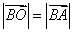 cos∠ABO=
cos∠ABO=
 。如果令平面α的法向量为
。如果令平面α的法向量为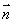 ,考虑到法向量的方向,可以得到B点到平面α的距离为
,考虑到法向量的方向,可以得到B点到平面α的距离为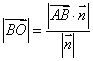 。
。
因此要求一个点到平面的距离,可以分以下几步完成:
1、求出该平面的一个法向量.
2、找出从该点出发的平面的任一条斜线段对应的向量.
3、求出法向量与斜线段向量的数量积的绝对值再除以法向量的模,即可求出点到平面的距离.
由于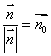 可以视为平面的单位法向量,所以点到平面的距离实质就是平面的单位法向量与从该点出发的斜线段向量的数量积的绝对值,即
可以视为平面的单位法向量,所以点到平面的距离实质就是平面的单位法向量与从该点出发的斜线段向量的数量积的绝对值,即 .
.
另外,等积法也是点到面距离的常用求法.
(二)线面距、面面距均可转化为点面距离用求点面距的方法进行求解。
(三)两异面直线距离的求法
如图(b)所示,设l1、l2是两条异面直线,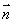 是l1与l2的公垂线段AB的方向向量,又C、D分别是l1、l2上的任意两点,则l1与l2的距离是
是l1与l2的公垂线段AB的方向向量,又C、D分别是l1、l2上的任意两点,则l1与l2的距离是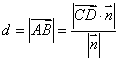 。
。
【典型例题】
例1. 设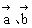 分别是直线l1、l2的方向向量,根据下列条件判断l1与l2的位置关系。
分别是直线l1、l2的方向向量,根据下列条件判断l1与l2的位置关系。
(1)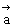 =(2,3,-1),
=(2,3,-1), =(-6,-9,3);
=(-6,-9,3);
(2)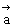 =(5,0,2),
=(5,0,2), =(0,4,0);
=(0,4,0);
(3)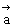 =(-2,1,4),
=(-2,1,4), =(6,3,3)
=(6,3,3)
例2. 设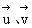 分别是平面α、β的法向量,根据下列条件判断α、β的位置关系:
分别是平面α、β的法向量,根据下列条件判断α、β的位置关系:
(1)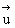 =(1,-1,2),
=(1,-1,2),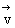 =(3,2,
=(3,2,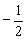 );
);
(2)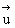 =(0,3,0),
=(0,3,0),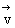 =(0,-5,0);
=(0,-5,0);
(3)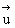 =(2,-3,4),
=(2,-3,4),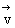 =(4,-2,1)。
=(4,-2,1)。
例3. 已知点A(3,0,0),B(0,4,0),C(0,0,5),求平面ABC的一个单位法向量。
例4. 若直线l的方向向量是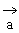 =(1,2,2),平面α的法向量是
=(1,2,2),平面α的法向量是 =(-1,3,0),试求直线l与平面α所成角的余弦值。
=(-1,3,0),试求直线l与平面α所成角的余弦值。
例5. 如图(a)所示,在正方体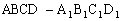 中,M、N分别是
中,M、N分别是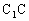 、
、 的中点。
的中点。
求证:(1)MN//平面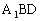 ;
;
(2)平面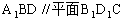 。
。
例6. 如图,在正方体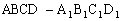 中,O为AC与BD的交点,G为CC1的中点。求证:A1O⊥平面GBD。
中,O为AC与BD的交点,G为CC1的中点。求证:A1O⊥平面GBD。
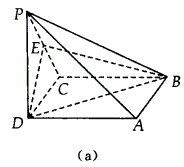
例7. (20##年天津)如图(a)所示,在四棱锥P—ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点。
(1)证明:PA//平面EDB;
(2)求EB与底面ABCD所成角的正切值。
例8. 正方体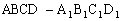 中,E、F分别是
中,E、F分别是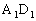 、
、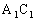 的中点,求:
的中点,求:
(1)异面直线AE与CF所成角的余弦值;
(2)二面角C—AE—F的余弦值的大小。
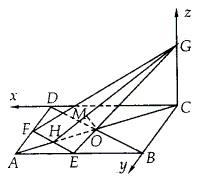
例9. 已知正方形ABCD的边长为4,E、F分别是AB、AD的中点,H是EF与AC的交点,CG⊥面ABCD,且CG=2。求BD到面EFG的距离。
-
空间几何体知识点总结(4)
空间几何体一棱柱1定义有两个面互相平行其余各面都是四边形并且每相邻两个四边形的公共边都互相平行由这些面所围成的几何体叫做棱柱2分类…
-
《空间几何体》知识点总结
空间几何体知识点总结一空间几何体的结构特征1多面体由若干个平面多边形围成的几何体旋转体把一个平面图形绕它所在平面内的一条定直线旋转…
-
高中数学必修2知识点总结01 空间几何体
高中数学必修2知识点总结01空间几何体几何学是研究现实世界中物体的形状大小与位置关系的数学学科而空间几何体是几何学的重要组成部分它…
-
空间几何体知识归纳
一几何图形的识读与描绘1现实生活中接触到的各种物体大多是由柱锥台球形状的物体组成我们研究空间几何体不仅要了解其结构从复杂的几何体中…
-
空间几何体知识点总结与练习题
空间几何体的表面积和体积圆柱侧面展开图是矩形长是圆柱底面圆周长宽是圆柱的高母线S圆柱侧2rlS圆柱表2rrl其中为r圆柱底面半径l…
-
立体几何知识点总结
一、平面通常用一个平行四边形来表示.平面常用希腊字母α、β、γ?或拉丁字母M、N、P来表示,也可用表示平行四边形的两个相对顶点字母…
-
人教A版高中数学必修2空间立体几何知识点归纳
第一章空间几何体知识点归纳围成的多面体叫做棱柱。1:中心投影平行投影(1)定义:几何体的正视图、侧视图和俯视图统称为几何体的三视图…
-
高中数学—立体几何知识点总结(精华版)
一.基本概念和原理:立体几何知识点1.公理1:如果一条直线上的两点在一个平面内,那么这条直线上的所有的点都在这个平面内。公理2:如…
-
高中数学立体几何知识点总结
一、立体几何初步'h特殊几何体表面积公式(c为底面周长,h为高,为斜高,l为母线)S直棱柱侧面积?chS正棱锥侧面积?S正棱台侧面…
-
空间向量与立体几何知识点总结zy
高二数学期末复习空间向量复习空间向量与立体几何知识点总结一基本概念1空间向量2相反向量3相等向量4共线向量5共面向量6方向向量7法…
-
空间向量与立体几何知识点归纳总结 学生版
空间向量与立体几何知识点归纳总结一.知识要点。1.空间向量的概念:在空间,____________________________…