高数 第1章 极限计算方法总结
极限计算方法总结
一、极限定义、运算法则和一些结果
1.定义:
数列极限、函数极限,课本42页的表格必须认真填写并掌握。
说明:(1)一些最简单的数列或函数的极限(极限值可以观察得到)都可以用上面的极限严格定义证明,例如: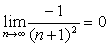 ;
; ;
;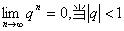 等。
等。
定义证明按着总结的四个步骤来,缺一不可!(2)在后面求极限时,(1)中提到的简单极限作为已知结果直接运用,而不需再用极限严格定义证明。
2.极限运算法则
定理1 已知 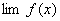 ,
,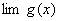 都存在,极限值分别为A,B,则下面极限都存在,
都存在,极限值分别为A,B,则下面极限都存在,
且(1)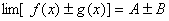 (2)
(2)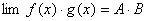
(3)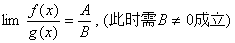 说明:极限号下面的极限过程是一致的;同时注意法则成立的条件,当条件不满足时,不能用。
说明:极限号下面的极限过程是一致的;同时注意法则成立的条件,当条件不满足时,不能用。
3.两个重要极限
(1) 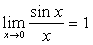 (2)
(2)  ;
; 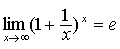
说明:(1)不仅要能够运用这两个重要极限本身,还应能够熟练运用它们的变形形式。
(2)一定注意两个重要极限成立的条件。
例如: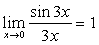 ,
,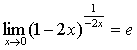 ,
, ;等等。
;等等。
4.等价无穷小
定理2 无穷小与有界函数的乘积仍然是无穷小(即极限是0)。
定理3 当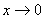 时,下列函数都是无穷小(即极限是0),且相互等价,即有:
时,下列函数都是无穷小(即极限是0),且相互等价,即有:
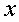 ~
~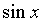 ~
~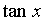 ~
~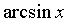 ~
~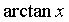 ~
~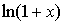 ~
~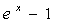 。
。
说明:当上面每个函数中的自变量x换成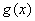 时(
时(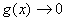 ),仍有上面的等价
),仍有上面的等价
关系成立,例如:当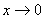 时,
时, 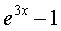 ~
~ 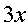 ;
;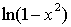 ~
~ 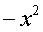 。
。
定理4 如果函数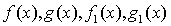 都是
都是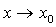 时的无穷小,且
时的无穷小,且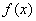 ~
~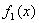 ,
,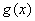 ~
~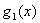 ,则当
,则当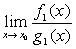 存在时,
存在时,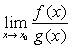 也存在且等于
也存在且等于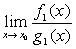 。
。
5.连续性
定理5 一切连续函数在其定义去间内的点处都连续,即如果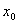 是函数
是函数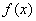 的定义去间内的一点,则有
的定义去间内的一点,则有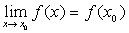 。求极限的一个方法。
。求极限的一个方法。
6.极限存在准则
定理6(准则1) 单调有界数列必有极限。
定理7(准则2) 已知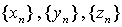 为三个数列,且满足:
为三个数列,且满足:
(1) 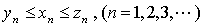 (2)
(2) 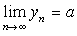 ,
,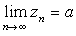
则极限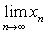 一定存在,且极限值也是a ,即
一定存在,且极限值也是a ,即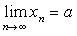 。
。
二、求极限方法举例
1. 用初等方法变形后,再利用极限运算法则求极限
例1 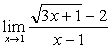
解:原式=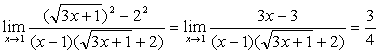 。
。
注:本题也可以用洛比达法则。
例2 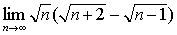
解:原式= 。
。
例3 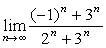
解:原式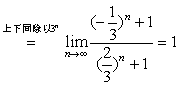 。
。
2. 利用函数的连续性(定理6)求极限
例4 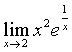
解:因为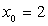 是函数
是函数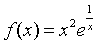 的一个连续点,
的一个连续点,
所以 原式=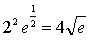 。
。
3. 利用两个重要极限求极限
例5 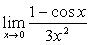
解:原式=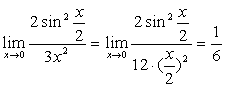 。
。
注:本题也可以用洛比达法则(第三章)
例6 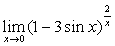
解:原式=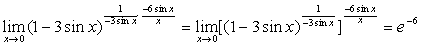 。
。
例7 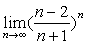
解:原式=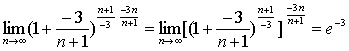 。
。
4. 利用定理2求极限
例8 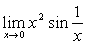
解:原式=0 (定理2的结果)。
5. 利用等价无穷小代换(定理4)求极限
例9 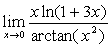
解: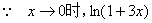 ~
~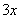 ,
,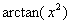 ~
~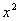 ,
, 原式=
原式=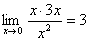 。
。
例10 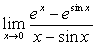
解:原式=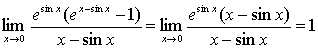 。
。
注:下面的解法是错误的:
原式=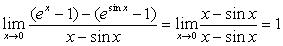 。
。
正如下面例题解法错误一样:
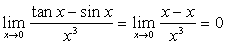 。
。
例11 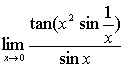
解: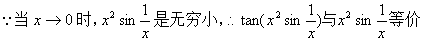 ,
,
所以, 原式=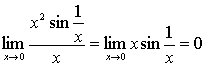 。(最后一步用到定理2)
。(最后一步用到定理2)
5. 利用极限存在准则求极限
例20 已知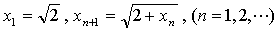 ,求
,求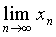
解:易证:数列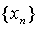 单调递增,且有界(0<
单调递增,且有界(0<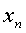 <2),由准则1极限
<2),由准则1极限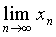 存在,设
存在,设 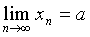 。对已知的递推公式
。对已知的递推公式 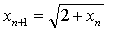 两边求极限,得:
两边求极限,得:
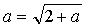 ,解得:
,解得: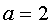 或
或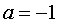 (不合题意,舍去)
(不合题意,舍去)
所以 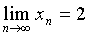 。
。
例21 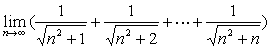
解: 易见: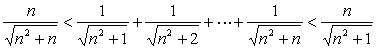
因为 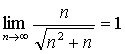 ,
,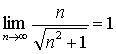
所以由准则2得: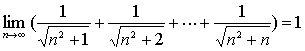 。
。
上面对求第一章极限的常用方法进行了比较全面的总结,由此可以看出,求极限方法灵活多样,而且许多题目不只用到一种方法,因此,要想熟练掌握各种方法,必须多做练习,在练习中体会。另外,求极限还有其它一些方法,如用洛必达、定积分求极限等,后面再作介绍。
第二篇:高等数学极限总结
【摘 要】《高等数学》教学中对于极限部分的要求很高,这主要是因为其特殊的地位决定的。然而极限部分绝大部分的运算令很多从中学进入高校的学生感到困窘。本文立足教材的基本概念阐述,着重介绍极限运算过程中极具技巧的解决思路。希望以此文能对学习者有所帮助。
【关键词】高等数学 极限 技巧
《高等数学》极限运算技巧
《高等数学》的极限与连续是前几章的内容,对于刚入高校的学生而言是入门部分的重要环节。是“初等数学”向“高等数学”的起步阶段。
一,极限的概念
从概念上来讲的话,我们首先要掌握逼近的思想,所谓极限就是当函数的变量具有某种变化趋势(这种变化趋势是具有唯一性),那么函数的应变量同时具有一种趋势,而且这种趋势是与自变量的变化具有对应性。通俗的来讲,函数值因为函数变量的变化而无限逼近某一定值,我们就将这一定值称为该函数在变量产生这种变化时的极限!
从数学式子上来讲,逼近是指函数的变化,表示为。这个问题不再赘述,大家可以参考教科书上的介绍。
二,极限的运算技巧
我在上课时,为了让学生好好参照我的结论,我夸过这样一个海口,我说,只要你认真的记住这些内容,高数部分所要求的极限内容基本可以全部解决。现在想来这不是什么海口,数学再难也是基本的内容,基本的方法,关键是技巧性。我记得blog中我做过一道极限题,当时有网友惊呼说太讨巧了!其实不是讨巧,是有规律可循的!今天我写的内容希望可以对大家的学习有帮助!
我们看到一道数学题的时候,首先是审题,做极限题,首先是看它的基本形式,是属于什么形式采用什么方法。这基本上时可以直接套用的。
1,连续函数的极限
这个我不细说,两句话,首先看是不是连续函数,是连续函数的直接带入自变量。
2,不定型
我相信所有学习者都很清楚不定型的重要性,确实。那么下面详细说明一些注意点以及技巧。
第一,所有的含有无穷小的,首先要想到等价无穷小代换,因为这是最能简化运算的。等价代换的公式主要有六个: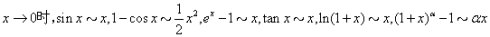
需要注意的是等价物穷小代换是有适用条件的,即:在含有加减运算的式子中不能直接代换,在部分式子的乘除因子也不能直接代换,那么如果一般方法解决不了问题的话,必须要等价代换的时候,必须拆项运算,不过,需要说明,拆项的时候要小心,必须要保证拆开的每一项极限都存在。
此外等价无穷小代换的使用,可以变通一些其他形式,比如: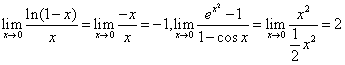 等等。特别强调在运算的之前,检验形式,是无穷小的形式才能等价代换。
等等。特别强调在运算的之前,检验形式,是无穷小的形式才能等价代换。
当然在一些无穷大的式子中也可以去转化代换,即无穷大的倒数是无穷小。这需要变通的看问题。
在无穷小的运算中,洛必答法则也是一种很重要的方法,但是洛必答法则适用条件比较单一,就是无穷小比无穷小。比较常见的采用洛必答法则的是无穷小乘无穷大的情况。(特别说明无穷小乘无穷大可以改写为无穷小比无穷小或者无穷大比无穷大的形式,这根据做题的需要来进行)。
第二,在含有∞的极限式中,一般可分为下面几种情况:
(1),“∞/∞ ”形式
如果是幂函数形式的(包含幂函数四则运算形式),可以找高次项,提出高次项,这样其他一切项就都是无穷小了,只有高次项是常数。比如: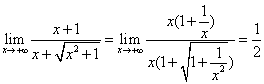 ,这道题中,可以看到提出最高次x(注意不是)其他项都是“0”,原来的x都是常数1了。当然如果分式形式中,只有分子中含有高次项,那么该极限式极限不存在(是无穷大),如果只有分母中含有高次项,那么该极限式极限为0,如果分子分母都含有高次项,我们可以直接去看高次项的系数,基本原理其实就是上面所说的提高次项。比如上面的例子,可以直接写1/2。
,这道题中,可以看到提出最高次x(注意不是)其他项都是“0”,原来的x都是常数1了。当然如果分式形式中,只有分子中含有高次项,那么该极限式极限不存在(是无穷大),如果只有分母中含有高次项,那么该极限式极限为0,如果分子分母都含有高次项,我们可以直接去看高次项的系数,基本原理其实就是上面所说的提高次项。比如上面的例子,可以直接写1/2。
如果不是纯幂函数形式,无法用提高次项的方法(提高次项是优先使用的方法),使用洛必达也是一种很好的方法。需要强调的是洛必达是一种解决“∞/∞ ”或“0/0 ”的基本方法,它的严格限制形式只有这两种,所以比较好观察。但是多数时候我们优先采用其他的方法来解决,这主要是考虑运算量的问题。
(2),“∞-∞ ”形式
“ ∞-∞”形式不能直接运算,需要转换形式,即转换成“∞/∞ ”或“0/0 ”的形式,基本解法同上。比如: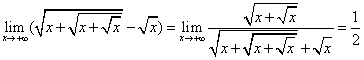
这道题是转换形式之后是“∞/∞ ”的形式,提高次项解。
(3)“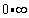 ”形式
”形式
这也是需要转换的一种基本形式。因为无穷大与无穷小之间的倒数关系,所以这种转换时比较简单也是比较容易解决的。转换之后的形式也是“∞/∞ ”或“0/0 ”的形式。
第三,“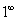 ”
”
这种形式的解决思路主要有两种。
第一种是极限公式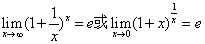 ,这种形式也是比较直观的。比如:
,这种形式也是比较直观的。比如: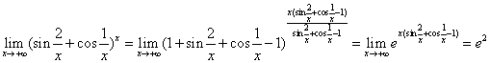 这道题的基本接替思路是,检验形式是“
这道题的基本接替思路是,检验形式是“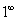 ”,然后选用公式,再凑出公式的形式,最后直接套用公式。
”,然后选用公式,再凑出公式的形式,最后直接套用公式。
第二种是取对数消指数。简单来说,“ 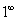 ”形式指数的存在是我们解题的主要困难。那么我们直接消掉指数就可以采用其他方法来解决了。比如上面那道题用取对数消指数的方法来解,是这样的:
”形式指数的存在是我们解题的主要困难。那么我们直接消掉指数就可以采用其他方法来解决了。比如上面那道题用取对数消指数的方法来解,是这样的: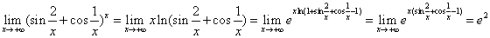
可以看出尽管思路切入点不一样,但是这两种方法有异曲同工之妙。
三,极限运算思维的培养
极限运算考察的是一种基本能力,所以在做题或者看书的时候依赖的是基本概念和基本方法。掌握一定的技巧可以使学习事半功倍。而极限思维的培养则是对做题起到指导性的意义。如何培养,一方面要立足概念,另一方面则需要在具体的运算中体会,多做题多总结。
-
高等数学中求极限的方法小结
宁波大红鹰学院学生数学课程论文高等数学中求极限的方法小结2求极限的常用方法21利用等价无穷小求极限这种方法的理论基础主要包括1有限…
-
高等数学求极限的常用方法(附例题和详解)
高等数学求极限的14种方法一、极限的定义1.极限的保号性很重要:设f(x)?A,注:它的使用有严格的使用前提。首先必须是X趋近,而…
-
高数中求极限的16种方法
高数中求极限的16种方法好东西假如高等数学是棵树木得话那么极限就是他的根函数就是他的皮树没有跟活不下去没有皮只能枯萎可见这一章的重…
-
高数求极限的16种方法(超经典)高彦辉总结
L.+'''+.+'''+.+天天快乐+'+..+'+.+爱爱爱爱祝爱爱愿爱爱你爱爱永爱爱远爱爱被爱爱爱爱爱包爱爱围爱爱爱爱爱爱爱…
-
高数 第1章 极限计算方法总结
极限计算方法总结一极限定义运算法则和一些结果1定义数列极限函数极限课本42页的表格必须认真填写并掌握说明1一些最简单的数列或函数的…
-
高等数学课程培训总结
20xx年x月x日在长春市分中心接受培训的学员围绕高等数学课程建设的一系列问题展开了热烈的讨论,全班同学首先肯定了这次培训的价值。…
-
考研.数学 高等数学总结1
中值定理及应用一、基本概念定理1、极值点与极值—设连续y?f(x)(x?D),其中x0?D。若存在??0,当0?|x?x0|??时…
-
高等数学(同济五版)难点总结及课后习题解读
习题解读基础阶段的复习是以课本为主,主要任务两个,一是学习知识点(定义、定理、公式)并理解它们,二是完成一定的课后习题以检验自己对…
-
大一高数第一章复习总结及相关习题
第一章函数与极限习题课一、主要内容(一)函数的定义(二)极限的概念(三)连续的概念一)函数1.函数的定义函数的分类2.函数的性质有…
- 高等数学第一章总结
-
求极限方法小结
一.横向总结:1.活用2个重要极限2.a有界函数与无穷小的乘积是无穷小b无穷小与无穷大的关系:无穷大的倒数为无穷小,恒不为零的无穷…