考研数学之高等数学讲义第一章(考点知识点+概念定理总结)
高等数学讲义
目 录
第一章 函数、极限、连续·················································· 1
第二章 一元函数微分学····················································· 24
第三章 一元函数积分学····················································· 49
第四章 常微分方程···························································· 70
第五章 向量代数与空间解析几何········································· 82
第六章 多元函数微分学····················································· 92
第七章 多元函数积分学····················································· 107
第八章 无穷级数(数一和数三)········································· 129
第一章 函数、极限、连续
§1.1 函数
(甲) 内容要点
一、函数的概念
1.函数的定义 2.分段函数 3.反函数 4.隐函数
二、基本初等函数的概念、性质和图象
三、复合函数与初等函数
四、考研数学中常出现的非初等函数
1.用极限表示的函数
(1) 
(2) 
2.用变上、下限积分表示的函数
(1)  其中
其中 连续,则
连续,则
(2)  其中
其中 可导,
可导, 连续,
连续,
则
五、函数的几种性质
1. 有界性:设函数 在X内有定义,若存在正数M,使
在X内有定义,若存在正数M,使 都有
都有 ,则称
,则称 在X上是有界的。
在X上是有界的。
2. 奇偶性:设区间X关于原点对称,若对 ,都有
,都有 ,则称
,则称 在X上是奇函数。
在X上是奇函数。
若对 ,都有
,都有 ,则称
,则称 在X上是偶函数,奇函数的图象关于原点对称;偶函数图象关于
在X上是偶函数,奇函数的图象关于原点对称;偶函数图象关于 轴对称。
轴对称。
3. 单调性:设 在X上有定义,若对任意
在X上有定义,若对任意 ,
, 都有
都有
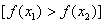 则称
则称 在X上是单调增加的[单调减少的];若对任意
在X上是单调增加的[单调减少的];若对任意 ,
,
 都有
都有 ,则称
,则称 在X上是单调不减[单调不增]
在X上是单调不减[单调不增]
(注意:有些书上把这里单调增加称为严格单调增加;把这里单调不减称为单调增加。)
4. 周期性:设 在X上有定义,如果存在常数
在X上有定义,如果存在常数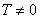 ,使得任意
,使得任意 ,
, ,都有
,都有 ,则称
,则称 是周期函数,称T为
是周期函数,称T为 的周期。
的周期。
由此可见,周期函数有无穷多个周期,一般我们把其中最小正周期称为周期。
§1.2 极限
(甲) 内容要点
一、极限的概念与基本性质
1.极限的概念
(1) 数列的极限
(2) 函数的极限 ;
; ;
;
 ;
; ;
;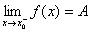
2.极限的基本性质
定理1 (极限的唯一性 ) 设 ,
, ,则A=B
,则A=B
定理2 (极限的不等式性质) 设 ,
,
若 变化一定以后,总有
变化一定以后,总有 ,则
,则
反之, ,则
,则 变化一定以后,有
变化一定以后,有 (注:当
(注:当 ,
, 情形也称为极限的保号性)
情形也称为极限的保号性)
定理3 (极限的局部有界性)设
则当 变化一定以后,
变化一定以后, 是有界的。
是有界的。
定理4 设 ,
,
则(1)
(2)
(3)
(4)
(5)

二、无穷小
1.无穷小定义:若 ,则称
,则称 为无穷小(注:无穷小与
为无穷小(注:无穷小与 的变化过程有关,
的变化过程有关, ,当
,当 时
时 为无穷小,而
为无穷小,而 或其它时,
或其它时, 不是无穷小)
不是无穷小)
2.无穷大定义:任给M>0,当 变化一定以后,总有
变化一定以后,总有 ,则称
,则称 为无穷大,记以
为无穷大,记以 。
。
3.无穷小与无穷大的关系:在 的同一个变化过程中,
的同一个变化过程中,
若 为无穷大,则
为无穷大,则 为无穷小,
为无穷小,
若 为无穷小,且
为无穷小,且 ,则
,则 为无穷大。
为无穷大。
4.无穷小与极限的关系:
 ,其中
,其中
5.两个无穷小的比较
设 ,
, ,且
,且
(1) ,称
,称 是比
是比 高阶的无穷小,记以
高阶的无穷小,记以
称 是比
是比 低阶的无穷小
低阶的无穷小
(2) ,称
,称 与
与 是同阶无穷小。
是同阶无穷小。
(3) ,称
,称 与
与 是等阶无穷小,记以
是等阶无穷小,记以
6.常见的等价无穷小,当 时
时
 ,
, ,
, ,
, ,
, ,
, ,
, ,
, 。
。
7.无穷小的重要性质
有界变量乘无穷小仍是无穷小。
三、求极限的方法
1.利用极限的四则运算和幂指数运算法则
2.两个准则
准则1:单调有界数列极限一定存在
(1) 若 (
( 为正整数)又
为正整数)又 (
( 为正整数),则
为正整数),则 存在,且
存在,且
(2) 若 (
( 为正整数)又
为正整数)又 (
( 为正整数),则
为正整数),则 存在,且
存在,且
准则2:夹逼定理
设 。若
。若 ,
, ,则
,则
3.两个重要公式
公式1:
公式2: ;
; ;
;
4.用无穷小重要性质和等价无穷小代换
5.用泰勒公式(比用等价无穷小更深刻)(数学一和数学二)
当 时,
时,


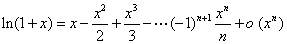


6.洛必达法则
法则1:( 型)设(1)
型)设(1)
(2) 变化过程中,
变化过程中, ,
, 皆存在
皆存在
(3) (或
(或 )
)
则 (或
(或 )
)
(注:如果 不存在且不是无穷大量情形,则不能得出
不存在且不是无穷大量情形,则不能得出 不存在且不是无穷大量情形)
不存在且不是无穷大量情形)
法则2:( 型)设(1)
型)设(1)
(2) 变化过程中,
变化过程中, ,
, 皆存在
皆存在
(3) (或
(或 )
)
则 (或
(或 )
)
7.利用导数定义求极限
基本公式: [如果存在]
[如果存在]
8.利用定积分定义求极限
基本公式 [如果存在]
[如果存在]
9.其它综合方法
10.求极限的反问题有关方法
§1.3 连续
(甲) 内容要点
一、函数连续的概念
1.函数在一点连续的概念
定义1 若 ,则称
,则称 在点
在点 处连续。
处连续。
定义2 设函数 ,如果
,如果 ,则称函数
,则称函数 在点
在点 处左连续;如果
处左连续;如果 ,则称函数
,则称函数 在点
在点 处右连续。
处右连续。
如果函数 在点
在点 处连续,则
处连续,则 在
在 处既是左连续,又是右连续。
处既是左连续,又是右连续。
2.函数在区间内(上)连续的定义
如果函数 在开区间(
在开区间( )内的每一点都连续,则称
)内的每一点都连续,则称 在
在 内连续。
内连续。
如果 在开区间内连续,在区间端点
在开区间内连续,在区间端点 右连续,在区间端点
右连续,在区间端点 左连续,则称
左连续,则称 在闭区间[
在闭区间[ ]上连续。
]上连续。
二、函数的间断点及其分类
1.函数的间断点的定义
如果函数 在点
在点 处不连续,则称
处不连续,则称 为
为 的间断点。
的间断点。
2.函数的间断点分为两类:
(1)第一类间断点
设 是函数
是函数 的间断点,如果
的间断点,如果 在间断点
在间断点 处的左、右极限都存在,则称
处的左、右极限都存在,则称 是
是 的第一类间断点。
的第一类间断点。
第一类间断点包括可去间断点和跳跃间断点。
(2)第二类间断点
第一类间断点以外的其他间断点统称为第二类间断点。
常见的第二类间断点有无穷间断点和振荡间断点。
例如: 是
是 的可去间断点,是
的可去间断点,是 的跳跃间断点,是
的跳跃间断点,是 的无穷间断点,是
的无穷间断点,是 的振荡间断点。
的振荡间断点。
三、初等函数的连续性
1.在区间I连续的函数的和、差、积及商(分母不为零),在区间I仍是连续的。
2.由连续函数经有限次复合而成的复合函数在定义区间内仍是连续函数。
3.在区间I连续且单调的函数的反函数,在对应区间仍连续且单调。
4.基本初等函数在它的定义域内是连续的。
5.初等函数在它的定义区间内是连续的。
四、闭区间上连续函数的性质
在闭区间[a ,b]上连续的函数 ,有以下几个基本性质,这些性质以后都要用到。
,有以下几个基本性质,这些性质以后都要用到。
定理1 (有界定理)如果函数f(x)在闭区间[a, b]上连续,则f(x)必在[a, b]上有界。
定理2 (最大值和最小值定理)如果函数f(x)在闭区间[a, b]上连续,则在这个区间上一定存在最大值M和最小值m.
其中最大值M和最小值m的定义如下:
定义 设 是区间
是区间 上某点
上某点 处的函数值,如果对于区间
处的函数值,如果对于区间 上的任一点
上的任一点 ,总有
,总有 ,则称
,则称 为函数
为函数 在
在 上的最大值。同样可以定义最小值
上的最大值。同样可以定义最小值 .
.
定理3 (介值定理)如果函数 在闭区间
在闭区间 上连续,且其最大值和最小值分别为
上连续,且其最大值和最小值分别为 和
和 ,则对于介于
,则对于介于 和
和 之间的任何实数
之间的任何实数 ,在
,在 上至少存在一个
上至少存在一个 ,使得
,使得

推论:如果函数 在闭区间
在闭区间 上连续,且
上连续,且 与
与 异号,则在
异号,则在 内至少存在一个点
内至少存在一个点 ,使得
,使得

这个推论也称零点定理。
思考题:什么情况下能保证推论中的 是唯一的?
是唯一的?
第二篇:考研数学之线性代数讲义(考点知识点+概念定理总结)
线性代数讲义
目录
第一讲 基本概念
线性方程组 矩阵与向量 初等变换和阶梯形矩阵 线性方程组的矩阵消元法
第二讲 行列式
完全展开式 化零降阶法 其它性质 克莱姆法则
第三讲 矩阵
乘法 乘积矩阵的列向量和行向量 矩阵分解 矩阵方程 逆矩阵 伴随矩阵
第四讲 向量组
线性表示 向量组的线性相关性 向量组的极大无关组和秩 矩阵的秩
第五讲 方程组
解的性质 解的情况的判别 基础解系和通解
第六讲 特征向量与特征值 相似与对角化
特征向量与特征值—概念,计算与应用 相似 对角化—判断与实现
附录一 内积 正交矩阵 施密特正交化 实对称矩阵的对角化
第七讲 二次型
二次型及其矩阵 可逆线性变量替换 实对称矩阵的合同 标准化和规范化 惯性指数 正定二次型与正定矩阵
附录二 向量空间及其子空间
附录三 两个线性方程组的解集的关系
附录四 06,07年考题
第一讲 基本概念
1.线性方程组的基本概念
线性方程组的一般形式为:
a11x1+a12x2+…+a1nxn=b1,
a21x1+a22x2+…+a2nxn=b2,
… … … …
am1x1+am2x2+…+amnxn=bm,
其中未知数的个数n和方程式的个数m不必相等.
线性方程组的解是一个n维向量(k1,k2, …,kn)(称为解向量),它满足:当每个方程中的未知数xi都用ki替代时都成为等式.
线性方程组的解的情况有三种:无解,唯一解,无穷多解.
对线性方程组讨论的主要问题两个:(1)判断解的情况.(2)求解,特别是在有无穷多接时求通解.
b1=b2=…=bm=0的线性方程组称为齐次线性方程组.
n维零向量总是齐次线性方程组的解,称为零解.因此齐次线性方程组解的情况只有两种:唯一解(即只要零解)和无穷多解(即有非零解).
把一个非齐次线性方程组的每个方程的常数项都换成0,所得到的齐次线性方程组称为原方程组的导出齐次线性方程组,简称导出组.
2.矩阵和向量
(1)基本概念
矩阵和向量都是描写事物形态的数量形式的发展.
由m´n个数排列成的一个m行n列的表格,两边界以圆括号或方括号,就成为一个m´n型矩阵.例如

为其系数矩阵和增广矩阵.增广矩阵体现了方程组的全部信息,而齐次方程组只用系数矩阵就体现其全部信息.
一个矩阵中的数称为它的元素,位于第i行第j列的数称为(i,j)位元素.
元素全为0的矩阵称为零矩阵,通常就记作0.
两个矩阵A和B相等(记作A=B),是指它的行数相等,列数也相等(即它们的类型相同),并且对应的元素都相等.
由n个数构成的有序数组称为一个n维向量,称这些数为它的分量.
书写中可用矩阵的形式来表示向量,例如分量依次是a1,a2,¼ ,an的向量可表示成

请注意,作为向量它们并没有区别,但是作为矩阵,它们不一样(左边是1´n矩阵,右边是n´1矩阵).习惯上把它们分别称为行向量和列向量.(请注意与下面规定的矩阵的行向量和列向量概念的区别.)
一个m´n的矩阵的每一行是一个n维向量,称为它的行向量; 每一列是一个m维向量, 称为它的列向量.常常用矩阵的列向量组来写出矩阵,例如当矩阵A的列向量组为a1, a2,¼ ,an时(它们都是表示为列的形式!)可记A=(a1, a2,¼ ,an).
矩阵的许多概念也可对向量来规定,如元素全为0的向量称为零向量,通常也记作0.两个向量a和b相等(记作a=b),是指它的维数相等,并且对应的分量都相等.
(2) 线性运算和转置
线性运算是矩阵和向量所共有的,下面以矩阵为例来说明.
加(减)法:两个m´n的矩阵A和B可以相加(减),得到的和(差)仍是m´n矩阵,记作
A+B (A-B),法则为对应元素相加(减).
数乘: 一个m´n的矩阵A与一个数c可以相乘,乘积仍为m´n的矩阵,记作cA,法则为A的每个元素乘c.
这两种运算统称为线性运算,它们满足以下规律:
① 加法交换律:A+B=B+A.
② 加法结合律:(A+B)+C=A+(B+C).
③ 加乘分配律:c(A+B)=cA+cB.(c+d)A=cA+dA.
④ 数乘结合律: c(d)A=(cd)A.
⑤ cA=0Û c=0 或A=0.
转置:把一个m´n的矩阵A行和列互换,得到的n´m的矩阵称为A的转置,记作A T(或A¢).
有以下规律:
① (AT)T=A.
② (A+B)T=AT+BT.
③ (cA)T=cAT.
转置是矩阵所特有的运算,如把转置的符号用在向量上,就意味着把这个向量看作矩阵了.当a是列向量时, a T表示行向量,当a是行向量时,a T表示列向量.
向量组的线性组合:设a1, a2,…,as是一组n维向量, c1,c2,…,cs是一组数,则称
c1a1+c2a2+…+csas
为a1, a2,…,as的(以c1,c2,…,cs为系数的)线性组合.
n维向量组的线性组合也是n维向量.
(3) n阶矩阵与几个特殊矩阵
行数和列数相等的矩阵称为方阵,行列数都为n的矩阵也常常叫做n阶矩阵.
把n阶矩阵的从左上到右下的对角线称为它对角线.(其上的元素行号与列号相等.)
下面列出几类常用的n阶矩阵,它们都是考试大纲中要求掌握的.
对角矩阵: 对角线外的的元素都为0的n阶矩阵.
单位矩阵: 对角线上的的元素都为1的对角矩阵,记作E(或I).
数量矩阵: 对角线上的的元素都等于一个常数c的对角矩阵,它就是cE.
上三角矩阵: 对角线下的的元素都为0的n阶矩阵.
下三角矩阵: 对角线上的的元素都为0的n阶矩阵.
对称矩阵:满足AT=A矩阵.也就是对任何i,j,(i,j)位的元素和(j,i)位的元素总是相等的n阶矩阵.
(反对称矩阵:满足AT=-A矩阵.也就是对任何i,j,(i,j)位的元素和(j ,i)位的元素之和总等于0的n阶矩阵.反对称矩阵对角线上的元素一定都是0.)
3. 矩阵的初等变换和阶梯形矩阵
矩阵有以下三种初等行变换:
① 交换两行的位置.
② 用一个非0的常数乘某一行的各元素.
③ 把某一行的倍数加到另一行上.(称这类变换为倍加变换)
类似地, 矩阵还有三种初等列变换,大家可以模仿着写出它们,这里省略了. 初等行变换与初等列变换统称初等变换.
阶梯形矩阵:一个矩阵称为阶梯形矩阵,如果满足:
① 如果它有零行,则都出现在下面.
② 如果它有非零行,则每个非零行的第一个非0元素所在的列号自上而下严格单调递增.
把阶梯形矩阵的每个非零行的第一个非0元素所在的位置称为台角.
简单阶梯形矩阵:是特殊的阶梯形矩阵,特点为:
③台角位置的元素为1.
④并且其正上方的元素都为0.
每个矩阵都可以用初等行变换化为阶梯形矩阵和简单阶梯形矩阵.这种运算是在线性代数的各类计算题中频繁运用的基本运算,必须十分熟练.
请注意: 1.一个矩阵用初等行变换化得的阶梯形矩阵并不是唯一的,但是其非零行数和台角位置是确定的.
2. 一个矩阵用初等行变换化得的简单阶梯形矩阵是唯一的.
4. 线性方程组的矩阵消元法
线性方程组的基本方法即中学课程中的消元法:用同解变换把方程组化为阶梯形方程组(即增广矩阵为阶梯形矩阵的方程组).
线性方程组的同解变换有三种:
① 交换两个方程的上下位置.
② 用一个非0的常数乘某个方程.
③ 把某个方程的倍数加到另一个方程上.
以上变换反映在增广矩阵上就是三种初等行变换.
线性方程组求解的基本方法是消元法,用增广矩阵或系数矩阵来进行,称为矩阵消元法. 对非齐次线性方程组步骤如下:
(1)写出方程组的增广矩阵(A|b),用初等行变换把它化为阶梯形矩阵(B|g).
(2)用(B|g)判别解的情况:
如果最下面的非零行为(0,0, ¼,0|d),则无解,否则有解.
有解时看非零行数r(r不会大于未知数个数n),r=n时唯一解;r
(推论:当方程的个数m
(3)有唯一解时求解的初等变换法:
去掉(B|g)的零行,得到一个n×(n+1)矩阵(B0|g0),并用初等行变换把它化为简单阶梯形矩阵(E|h),则h就是解.
对齐次线性方程组:
(1)写出方程组的系数矩阵A,用初等行变换把它化为阶梯形矩阵B.
(2)用B判别解的情况:非零行数r=n时只有零解;r推论:当方程的个数m
讨论题
1.设A是n阶矩阵,则
(A) A是上三角矩阵ÞA是阶梯形矩阵.
(B) A是上三角矩阵ÜA是阶梯形矩阵.
(C) A是上三角矩阵ÛA是阶梯形矩阵.
(D) A是上三角矩阵与A是阶梯形矩阵没有直接的因果关系.
2.下列命题中哪几个成立?
(1) 如果A是阶梯形矩阵,则A去掉任何一行还是是阶梯形矩阵.
(2) 如果A是阶梯形矩阵,则A去掉任何一列还是是阶梯形矩阵.
(3) 如果(A|B)是阶梯形矩阵,则A也是阶梯形矩阵.
(4) 如果(A|B)是阶梯形矩阵,则B也是阶梯形矩阵.
(5) 如果  是阶梯形矩阵,则A和B都是阶梯形矩阵.
是阶梯形矩阵,则A和B都是阶梯形矩阵.
第二讲 行列式
一.概念复习
1. 形式和意义
形式:用n2个数排列成的一个n行n列的表格,两边界以竖线,就成为一个n阶行列式:

如果行列式的列向量组为a1, a2, … ,an,则此行列式可表示为|a1, a2, … ,an|.
意义:是一个算式,把这n2个元素按照一定的法则进行运算,得到的数值称为这个行列式的值.
请注意行列式和矩阵在形式上和意义上的区别.
当两个行列式的值相等时,就可以在它们之间写等号! (不必形式一样,甚至阶数可不同.)
每个n阶矩阵A对应一个n阶行列式,记作|A|.
行列式这一讲的的核心问题是值的计算,以及判断一个行列式的值是否为0.
2. 定义(完全展开式)
2阶和3阶行列式的计算公式:

的值是许多项的代数和,每一项都是取自不同行,不同列的n个元素的乘积,其一般形式为:
 ,
,
这里把相乘的n个元素按照行标的大小顺序排列,它们的列标j1j2…jn构成1,2, …,n的一个全排列(称为一个n元排列),共有n!个n元排列,每个n元排列对应一项,因此共有n!个项.
所谓代数和是在求总和时每项先要乘+1或-1.规定t(j1j2…jn)为全排列j1j2…jn的逆序数(意义见下面),则项 所乘的是
所乘的是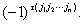
全排列的逆序数即小数排列在大数右面的现象出现的个数.
逆序数可如下计算:标出每个数右面比它小的数的个数,它们的和就是逆序数.例如求436512的逆序数:
 , t(436512)=3+2+3+2+0+0=10.
, t(436512)=3+2+3+2+0+0=10.
至此我们可以写出n阶行列式的值:

这里 表示对所有n元排列求和.称此式为n阶行列式的完全展开式.
表示对所有n元排列求和.称此式为n阶行列式的完全展开式.
用完全展开式求行列式的值一般来说工作量很大.只在有大量元素为0,使得只有少数项不为0时,才可能用它作行列式的计算.例如对角行列式,上(下)三角行列式的值就等于主对角线上的元素的乘积,因为其它项都为0.
2. 化零降阶法
把n阶行列式的第i行和第j列划去后所得到的n-1阶行列式称为(i,j)位元素aij的余子式,记作Mij.称Aij=(-1)i+jMij为元素aij的代数余子式.
定理(对某一行或列的展开)行列式的值等于该行(列)的各元素与其代数余子式乘积之和.
命题 第三类初等变换(倍加变换)不改变行列式的值.
化零降阶法 用命题把行列式的某一行或列化到只有一个元素不为0,再用定理.于是化为计算一个低1阶的行列式.
化零降阶法是实际计算行列式的主要方法,因此应该熟练掌握.
3.其它性质
行列式还有以下性质:
① 把行列式转置值不变,即|AT|=|A| .
② 某一行(列)的公因子可提出.
于是, |cA|=cn|A|.
③ 对一行或一列可分解,即如果某个行(列)向量a=b+g ,则原行列式等于两个行列式之和,这两个行列式分别是把原行列式的该行(列)向量a换为b或g 所得到的行列式.例如
|a,b1+b2,g |=|a,b1,g |+|a,b2,g |.?
④ 把两个行(列)向量交换, 行列式的值变号.
⑤ 如果一个行(列)向量是另一个行(列)向量的倍数,则行列式的值为0.
⑥ 某一行(列)的各元素与另一行(列)的对应元素的代数余子式乘积之和=0.
⑦ 如果A与B都是方阵(不必同阶),则

的行列式(或其转置).它由a1,a2 ,a3,…,an所决定,它的值等于

因此范德蒙行列式不等于0Û a1,a2 ,a3,…,an两两不同.
对于元素有规律的行列式(包括n阶行列式),常常可利用性质简化计算,例如直接化为三角行列式等.
4.克莱姆法则
克莱姆法则 应用在线性方程组的方程个数等于未知数个数n (即系数矩阵为n阶矩阵)的情形.此时,如果它的系数矩阵的行列式的值不等于0,则方程组有唯一解,这个解为
(D1/D, D2/D,¼,Dn/D),
这里D是系数行列式的值, Di是把系数行列式的第i个列向量换成常数列向量所得到的行列式的值.
说明与改进:
按法则给的公式求解计算量太大,没有实用价值.因此法则的主要意义在理论上,用在对解的唯一性的判断,而在这方面法则不够. 法则的改进:系数行列式不等于0是唯一解的充分必要条件.
实际上求解可用初等变换法:对增广矩阵(A|b)作初等行变换,使得A变为单位矩阵:
(A|b)®(E|h),
h就是解.
用在齐次方程组上 :如果齐次方程组的系数矩阵A是方阵,则它只有零解的充分必要条件是|A|¹0.
二. 典型例题
1.利用性质计算元素有规律的行列式




参考答案
例1 ①(2+4a)(2-a)4.② x3(x+4). ③ a3(a+10).
例2 1875.
例3 x1x2x3x4+x2x3x4+x1x3x4+x1x2x4+x1x2x3.
例4 (a+b+c)(a+b-c)(a-b+c)(a-b-c).
例5 1-a+a2-a3+a4-a5.
例6 9,-6
例7 1,-10.
例8 40.
例9 x=0,y=3,z=-1.
例10 -28.
例14 x1=a,x2=b,x3=c..
第三讲 矩阵
一.概念复习
1. 矩阵乘法的定义和性质
定义2.1 当矩阵A的列数和B的行数相等时,和A和B可以相乘,乘积记作AB. AB的行数和A相等,列数和B相等. AB的(i,j)位元素等于A的第i个行向量和B的第j个列向量(维数相同)对应分量乘积之和.

矩阵的乘法在规则上与数的乘法有不同:
① 矩阵乘法有条件.
② 矩阵乘法无交换律.
③ 矩阵乘法无消去律,即一般地
由AB=0推不出A=0或B=0.
由AB=AC和A¹0推不出B=C.(无左消去律)
由BA=CA和A¹0推不出B=C. (无右消去律)
请注意不要犯一种常见的错误:把数的乘法的性质简单地搬用到矩阵乘法中来.
矩阵乘法适合以下法则:
① 加乘分配律 A(B+C)= AB+AC,(A+B)C=AC+BC.
② 数乘性质 (cA)B=c(AB).
③ 结合律 (AB)C= A(BC).
④ (AB)T=B TA T.
2. n阶矩阵的方幂和多项式
任何两个n阶矩阵A和B都可以相乘,乘积AB仍是n阶矩阵.并且有行列式性质:
|AB|=|A||B|.
如果AB=BA,则说A和B可交换.
方幂 设k是正整数, n阶矩阵A的k次方幂A k即k个A的连乘积.规定A 0=E.
显然A的任何两个方幂都是可交换的,并且方幂运算符合指数法则:
① A kA h= A k+h.
② (A k)h= A kh.
但是一般地(AB)k和A kB k不一定相等!
n阶矩阵的多项式
设f(x)=amxm+am-1xm-1+…+a1x+a0,对n阶矩阵A规定
f(A)=amA m+am-1A m-1+…+ a1A+a0E.
称为A的一个多项式.请特别注意在常数项上加单位矩阵E.
乘法公式 一般地,由于交换性的障碍,小代数中的数的因式分解和乘法公式对于n阶矩阵的不再成立.但是如果公式中所出现的n阶矩阵互相都是乘法交换的,则乘法公式成立.例如
当A和B可交换时,有:
(A±B)2=A2±2AB+B2;
A2-B2=(A+B)(A-B)=(A+B)(A-B).
二项展开式成立:  等等.
等等.
前面两式成立还是A和B可交换的充分必要条件.
同一个n阶矩阵的两个多项式总是可交换的. 一个n阶矩阵的多项式可以因式分解.
-
高中数学必修1知识点总结:第一章_集合与函数概念
高中数学必修1知识点总结第一章集合与函数概念111集合的含义与表示1集合的概念集合中的元素具有确定性互异性和无序性2常用数集及其记…
-
高一数学必修1第一章知识点总结
一、集合有关概念1.集合的含义2.集合的中元素的三个特性:(1)元素的确定性,(2)元素的互异性,(3)元素的无序性,3.集合的表…
-
高中数学必修1知识点总结归纳:第一章_集合与函数概念
高中数学必修1知识点总结第一章集合与函数概念111集合的含义与表示1集合的概念集合中的元素具有确定性互异性和无序性2常用数集及其记…
-
高中高一数学必修1各章知识点总结
高中高一数学必修1各章知识点总结第一章集合与函数概念一集合有关概念1集合的含义某些指定的对象集在一起就成为一个集合其中每一个对象叫…
-
高中数学必修1知识点总结:第一章_集合与函数概念
高中数学必修1知识点总结第一章集合与函数概念111集合的含义与表示1集合的概念集合中的元素具有确定性互异性和无序性2常用数集及其记…
-
高等数学课程培训总结
20xx年x月x日在长春市分中心接受培训的学员围绕高等数学课程建设的一系列问题展开了热烈的讨论,全班同学首先肯定了这次培训的价值。…
-
考研.数学 高等数学总结1
中值定理及应用一、基本概念定理1、极值点与极值—设连续y?f(x)(x?D),其中x0?D。若存在??0,当0?|x?x0|??时…
-
高等数学(同济五版)难点总结及课后习题解读
习题解读基础阶段的复习是以课本为主,主要任务两个,一是学习知识点(定义、定理、公式)并理解它们,二是完成一定的课后习题以检验自己对…
-
大一高数第一章复习总结及相关习题
第一章函数与极限习题课一、主要内容(一)函数的定义(二)极限的概念(三)连续的概念一)函数1.函数的定义函数的分类2.函数的性质有…
- 高等数学第一章总结
-
高中数学必修5__第一章_解三角形复习知识点总结与练习
高中数学必修5第一章解三角形复习一、知识点总结【正弦定理】1.正弦定理:abc???2R(R为三角形外接圆的半径).sinAsin…