瓷砖知识大总结

瓷砖知识大总结！

瓷砖按照功能分为地砖、墙砖及腰线砖等。

地砖：按花色分为仿西班牙砖、玻化抛光砖、釉面砖、防滑砖及渗花抛光砖等。

墙砖：按花色可分为玻化墙砖、印花墙砖。

腰线砖：多为印花砖。为了配合墙砖的规格，腰线砖一般定为60mm×200mm的幅面。

瓷砖按工艺分为:釉面砖、通体砖、抛光砖、玻化砖、陶瓷锦砖。

釉面砖:指砖表面烧有釉层的砖。这种砖分为两类:一是用陶土烧制的;另一种是用瓷土烧制的,目前的家庭装修约80%的购买者选此砖为地面装饰材料。

通体砖:这是一种不上釉的瓷质砖,有很好的防滑性和耐磨性。一般所说的"防滑地砖"大部分是通体砖。由于这种砖价位适中,颇受消费者喜爱。

抛光砖:通体砖经抛光后就成为抛光砖,这种砖的硬度很高,非常耐磨。

玻化砖:这是一种高温烧制的瓷质砖,是所有瓷砖中最硬的一种。有时抛光砖被刮出划痕时,玻化砖仍然安然无恙。。

陶瓷锦砖：又名马赛克，规格多，薄而小，质地坚硬，耐酸、耐碱、耐磨、不渗水，抗压力强，不易破碎，彩色多样，用途广泛。

地砖的一般种类和特性

墙地砖一般指瓷砖。它具有防水防潮、耐磨、容易清洁等优点，对于潮湿或常需保持卫生的空间，如厨房、浴室等最为合用。

事实上，适用于地板铺饰的地砖有很多种类选择，常见的包括马赛克、高温砖、过底砖、粘土砖等。马赛克:马赛克的体积是各种地砖中最细小的，一般俗称为块砖。因其面积小巧，铺砌作地板，不易让人滑倒，特别适合湿滑环境，所以常用来铺砌家居中的厨房、浴室，或公众地方的大堂、游泳池等。其实马赛克在质材、颜色方面的选择相当丰富，在美感方面的营造有很大潜力，只要设计得宜，可以制造出不俗的视觉效果。

高温砖:近年较流行的地砖材料是高温砖。高温砖是以高温高压制而成的，较普通地砖具有较高的抗磨损能力，所以相当适合用作地板的饰材。一般高温砖的表面都相当光滑，而且品质佳的砖面，经过特别处理，即使沾水，也不容易滑倒。由于高温砖的颜色、质面光洁吸引，现在已有不少家庭用以铺砌起居室的地板，使高温砖除了在厨房、浴室出现外，也开始出现在厅堂。

过底砖:大多数的地砖由于由釉彩与砖板组成，若质料不佳或长期磨损，表面的釉便会刮花或脱落，露出底层砖板，无法修补。过底砖即弥补了这一缺点。这种砖是整块以同一材料制成，不分底层、表层，即使遭到刮割磨损，也不会露出另一种颜色的物料，影响美观；而且这种砖的抗磨损能力也相当强，适合用作走动量高的地板，故此现今也有不少人采用过底砖来铺砌地板。过底砖有哑面和光面的选择，其中光面的透底砖又名亮面砖，表面磨光，造成光滑镜面，具有云石的效果。

粘土砖:除了上述的地砖外，也有不少崇尚乡土风味的人士选择外型质感俭朴自然的粘土砖（红砖）来铺砌地板，较常见的是应用在阳台、花园，也有使用在厅堂中的。粘土砖是不上釉的地砖，给人朴实的质感，另外也可以加上水晶漆作面层的保护，以增添光滑的感觉。地砖防潮易清理，但要注意一些问题：留意瓷砖抗滑的效果，并非所有瓷砖沾水后均能防滑，可以尝试利用样本自行测试；若家中有小孩或老人家，更需要考虑碰撞等安全问题。

瓷砖选购前要注意的一些问题

作为一个普通的消费者，大家在选购瓷砖时往往会感到很茫然，经常会不知道作和选择。在下定单前要注意一些什么样的问题，在这里，我就个人的一些想法写出来，以供大家参考，希望能对大家有些帮助。

1）预算中容易被忽视的环节。

现在大家对瓷砖的价格都比较敏感，在采购时都会特别的注意，但是最后，在订购时却发现还是会大大的超支，这是什么原因呢？其实这就是在做预算时忽略了一些了环节。具体来讲有以下一些方面：墙砖：

由于墙砖配套的花砖和腰线都是单独计算，所以不仅要考虑砖的价格，同时要考虑花砖腰线的价格。在市场上咨询、采价时不仅要记砖的价格，同时要记配套的花砖腰线的价格。

地砖：

除了砖本身的价格之外，还应注意的方面就是踢角线的价格。铺设地砖时是否要做地拼花、有无特殊加工的地方都得考虑。

2）确定什么样的砖是好砖。

现在大家普遍都认为的是知名的品牌的产品是最好的，其实，这种观点我个人认为是值得怀疑的。知名的产品也罢，非知名的产品也巴，关键的是适合自己的砖才是最好的。打个比方，800铺起来大气，但是家里厅也就20来平的话，也不适用；进口砖不错，但是由于大米有限，买了之后，家里天天那口锅都存在问题的话，也是很不现实的。所以，适用的、适合自己的瓷砖产品才是最好的。

3）多向朋友咨询，了解产品的性价比。

大家可以通过各种途径多了解瓷砖方面的知识、选购的技巧。装修论坛、家居网站等都是一个不错的方法和途径，各方面的专家都有，同时又能热心的为大家答疑解惑，当然，瓷砖方面，来我的“陶瓷咨询中心”找我老六咨询就是一个不错的选择哦！

4）不要忽视了对商家实力、售后服务的考察。

在选购产品时除了考虑产品的品牌、价格等因素之外，千万不要忽视了商家实力、售后能力的考察。一个丁点小的门联儿，十来牌子的店铺里面的东东你敢选择吗？你能指望他的售后服务有多好吗？所以尽量的考虑那些实力大、操作规范的商家订购产品。同时，对于，售后方面的问题更是要不厌其烦的问清楚，退补货问题，质量问题的解决方式等作到清清楚楚，我要说的是没有哪个品牌的不会出质量问题，只有把这些落实清楚之后，方可下单子，以作到防范于未然吗。

挑选瓷砖的要点

在选择地砖的时候，可根据个人的爱好和居室的功能要求，根据实地布局，从地砖的规格、色调、质地等方面进行筛选。

质量好的地砖规格大小统一、厚度均匀，地砖表面平整光滑、无气泡、无污点、无麻面、色彩鲜明、均匀有光泽、边角无缺陷、９０度直角、不变形，花纹图案清晰，抗压性能好，不易坏损。

购买时您应根据自己的资金状况、喜好来决定砖的品种、颜色或图案，根据房间大小来决定尺寸。

先从包装箱中任意取出一片，看表面是否平整、完好，釉面应均匀、光亮、无斑点、缺釉、磕碰现象，四周边缘规整。釉面不光亮、发涩、或有气泡都属质量问题。

其次，再取出一片砖，两片对齐，中间缝隙越小越好。如果是图案砖必须用四片才能拼凑出一个完整图案来，还应看好砖的图案是否衔接、清晰。然后将一箱砖全部取出，平摆在一个大平面上，从稍远地方看整个效果，不论白色、其他色或图案，应色泽一致，如有个别砖深点、浅点，这样会很难看，影响整个装饰效果。

瓷砖数量的计算方式

墙地砖主要用于客厅、厨房、卫生间、阳台墙地面及局部背景墙。选购前应确认所需瓷砖的平方米或片数，数据取得有两种方法：

一种是根据工长测量提供数量。另一种是需要我们通过平面图计算出来：地砖面积=长×宽×（1+5%损耗）；墙砖面积=周长×高×（1+10%损耗）；片数≈面积/单片面积；腰线片数=周长/腰线长度+1；

花砖片数由客户自定，一般情况一面墙一块。确定墙地砖数量时尽量留出损耗，以免出现多次补货现象及由多次补货引起的色差，多余的砖未泡水未损坏的情况下可以退。订货时需标注产品规格、型号及使用位置。

瓷砖色彩搭配及形式搭配的基本原则

瓷砖产品的色彩十分丰富，而面对琳琅满目的瓷砖，消费者应如何选购和搭配呢？瓷砖色彩有六个原则：原则1：深色和浅色搭配，如黑与白、深与浅、深绿与浅灰都可以搭配使用。

原则2：相似色搭配，如黄与绿、红与紫、红与橙、橙与黄。

原则3：同类色搭配，如浅黄与深黄、黑色与灰色的搭配。

原则4：冷色与暖色的搭配，冷暖色的关系是依靠对比，由人的自然生活经验而产生，搭配起来也很有特 2

色。

原则5：无极色与颜色搭配，黑、白、金、银、灰被称为无极色，它们可以和任何颜色进行搭配。原则6：对比色的搭配，比如红与绿、黄与紫、蓝与橙、黑与白。

在实际使用中通常是几种方法同时运用。在具体铺贴中，色彩的搭配应该确定一种颜色为主色调，与另一种或几种颜色组成主次关系分明的搭配，切忌各种色彩分量相等的搭配。

形式搭配的四个原则是：

原则1：大与小的搭配，在面积的大小对比中追求搭配上的平衡。

原则2：方与圆的搭配，形态上的搭配点缀，能够取得大面积的协调效果，避免单调乏味。

原则3：点与面的搭配，点面结合可以避免铺贴上的简单乏味。

原则4：长与短的搭配，在大同里取得差异，对比中产生变化。

总之，形式的搭配应该追求大统一、小对比的原则。当然，具体的搭配应用还要结合周围环境以及使用者的喜好等因素来合理进行。

如何选购瓷砖

对于首次装修的业主，瓷砖的选择不是一件容易的事。走进建材城，不同品牌、颜色、价位的瓷砖琳琅满目，怎样选择谁是正确的呢？外行看热闹，内行看门道。其实其中的门道一点就破。

一要看品牌质量。有的小厂家靠压低生产成本来打疯狂价格战。殊不知瓷砖是要陪你很多年的物件，贪图钱包的一时节省，买了小厂家不耐磨的瓷砖，一年后砖表面斑斑驳驳、裂纹横生、不堪入目。花钱重新铺砖吧，一来已铺好的各种电、气管线不好轻易动它；二来二次装修的杂乱喧闹又搅得全家鸡犬不宁。更严重的是有的厂家为压低成本，生产出的产品不环保，这些铺在墙上、地上的“毒源”天天威胁着家人的身体健康。所以建议消费者还是选择品牌砖。

国产一线品牌瓷砖价格也并不昂贵，两、三千元就能搞掂30多平米的客厅。一般国内一线品牌瓷砖如奥米茄、亚细亚、罗马等都属于健康环保建材。例如奥米茄的产品要经过200多分钟二次高温煅烧，产品吸水率极低，砖面毛孔极小使污渍难以渗入产品。这样一来瓷砖打理起来也比较方便。

二要看瓷砖的图案设计风格。要综合考虑自己家里的家具及整体风格。比如说如果你是整日奔忙的办公室一族，可能会喜欢奥米茄浪漫、休闲、舒适的意大利风格。如果你是艺术感敏锐，追求时尚与精品生活的白领女性，可能会更倾向于西班牙进口的正中花砖点缀。如果你是传统型主妇，那么在淡色釉面砖系列中的选择余地就更大了。

三是要赶季节选购。装修旺季各品牌往往会有促销活动。在旺季中选购既省了钱包，又因在合适的季节铺贴瓷砖而保证了装修品质。

在瓷砖使用时要仔细阅读厂家须知。重信誉、重服务的正规厂家一般会附有很详细的说明。消费者使用前应检查外包装标明的色号、尺寸是否是自己订购的型号，同一色号的砖是否有色差、断线等缺陷。只有使用同一色号，才可以使用邻近色号以求色泽均一。铺贴前，瓷砖往往需要在清水内浸泡20-30分钟，滤去水份后才可进行铺贴。铺贴所用水泥标号应采用低标号，水泥厚度不要过大，一般不大于5mm。

一言以蔽之，旺季去选择品牌的瓷砖可以放心质量与环保，钱包也不必太受伤。花色品种的要求就仁者见仁、智者见智，看自己的喜好了。

如何选择墙地砖

选购墙地砖，要注意其吸水率，品质高的墙地砖，吸水率很低。吸水率较高的墙地砖经冷缩热胀后便会导致瓷砖表面龟裂及整块墙地砖剥落，当环境四季分明又潮湿，更需注意此问题。若墙地砖没有注明吸水率，则可以茶或水滴在墙地砖的背面，数分钟后视察水滴的扩散程度，越不吸水，即表示吸水率低，品质较佳。此外，要注意砖面是否平整，是否出现粗细不均的针孔，并可敲击瓷砖倾听声音是否清脆，声音越脆，即表示瓷砖的质地密度高，硬度较佳。并可试以硬物刮擦砖表面，若出现刮痕，则表示施釉不足，表面的釉磨光后，砖面便容易藏污，较难清理。

进行色差的判别。由于墙地砖一次购买的数量较大，多个包装之间如有明显色差，装修效果就很受影响，要对所有包装的产品抽样对比，观察色差的变化，色差大的一般不能选用。

要对规格尺寸进行逐一检验，尺寸误差大于0.5毫米，平整度大于0.1毫米的产品，不仅会增加施工的难度，同时装修后的效果差，也不能用于工程施工。

从价格分析，一般国产釉面墙砖，一等品价格在每平方米40元左右，深色彩釉价格略高于浅色彩釉砖价格，加上辅助材料及人工费用等，造价在每平方米80元左右。进口的彩釉墙面砖价格比国产的高1－3倍，每平方米价格在80－170元之间。

没上釉的地砖，一般不宜铺在潮湿而密闭的环境，因为砖块上的气孔吸水汽而无法发散，会导致霉菌出现。墙砖地砖不能混用

“反常规”地使用材料，比如把颜色艳丽的花墙面砖敲碎了铺在卫生间的地上，再把素雅一色的地面砖贴上墙，这样看似与众不同，但是专家告诫：这样做既不科学又不安全，墙砖和地砖是不能混着用的。地砖墙砖吸水率不同

室内瓷砖按铺贴地点分为墙砖和地砖。严格讲墙瓷砖属于陶制品，地砖通常是瓷制品，它们的物理特性不同，两者从选黏土配料到烧制工艺都有很大区别，墙面砖吸水率大概10％左右，比吸水率只有1％的地面砖要高出数倍。卫生间和厨房的地面应铺设吸水率低的地面砖，因为地面会经常用大量的清水洗刷，这样瓷砖才能不受水汽的影响、不吸纳污渍。墙砖是釉面陶制的，含水率比较高，它的背面一般比较粗糙，这也有利于黏合剂把墙面砖贴上墙。地砖不易在墙上贴牢固，墙砖用在地面会吸水太多而变得不易清洁，可见墙、地面砖不能混用。

铺前要找平

贴砖前应清理基层，如墙面上有石灰膏、乳胶漆、壁纸等装饰物，或地面上有污物，一定要清理干净，否则水泥砂浆与基层黏结不牢；另外，如果墙体自身有裂缝，应做妥善处理后才可贴砖，以免日后基本结构裂缝变大导致墙面砖开裂或脱落；还有，对于平整度或垂直度差距太大的地面、墙面，还要用水泥砂浆进行找平处理。

铺设顺序有讲究

贴地面砖应由内向外贴，如地面有坡度或有地漏儿，应注意按排水方向找坡；墙砖应从下向上铺贴，为美观起见，最底层的砖应后贴。墙砖贴完后再压地砖，遇有半块砖时，应尽量放在下面。另外，一面墙不能一次贴到顶，以防瓷砖自重较大，引起塌落。墙砖要充分浸泡

墙面砖有着较高的含水率，在粘贴时必须考虑到这一特性。贴砖前基层应充分浇水湿润，瓷砖也应在水中浸泡至少20分钟后方可使用。否则，砂浆中的水分被干燥的基层和瓷砖迅速吸收而快速凝结，会影响其黏结牢度。墙砖也会从水泥里吸收水分，使水泥无法起到粘贴剂的作用。另外，每种品牌墙面砖的吸水率也不相同，这点要靠经验来掌握。。

瓷砖粘贴、保养的学问

瓷砖（包括地砖）是住宅卫浴、厨房最常用的装饰材料。瓷砖在使用过程中常出现松动、脱落、渗水等问题，给人们带来很大烦恼，可使用石材粘结剂、外墙防水剂解决这些问题。

防松动，脱落

目前瓷砖粘贴大多采用水泥砂浆作粘结剂。它粘结牢度不够，而且由于长期处在潮湿、渗水、浸水环境下，易造成瓷砖的松动和脱落。水泥砂浆中加入107胶虽能提高粘结强度，但效果也不理想。采用树脂型粘结剂粘贴瓷砖，不仅粘结强度可达到或超过瓷、地砖，甚至大理石的本体强度，而且长期浸泡在水中也不会造成脱落。

防渗水

由于瓷砖拼缝处及粘贴层都极易渗水，会造成相邻居室内墙返潮，使涂料层剥落或墙纸损坏。装饰在外墙面的马赛克类瓷砖，经不起长久的风吹雨打，渗水返潮现象尤为严重。使用树脂形石材粘结再结合使用外墙防水剂即可解决。

旧瓷砖面加贴瓷砖

旧瓷砖要翻新，一般要求瓷砖要全部铲清，劳动强度很大。如欲在旧瓷砖上加贴新瓷砖，则水泥砂浆很难胜任，此时必须用树脂型石材粘结剂，它不怕瓷砖上油腻、污渍，而且有较好的粘结强度。

瓷砖的保养

瓷砖常会被油腻、水绣、皂垢等玷污，尤其瓷砖接缝处更易藏污纳垢。为保持瓷面清洁又不损坏瓷面光亮，可以使用多功能去污膏进行清洁。至于瓷砖缝隙处，则应先使用牙刷蘸少许去污膏去污垢，再在缝隙处用毛笔刷一道防水剂即可，这样不仅能防渗水且能防霉菌生长。

瓷砖安装的注意事项

贴砖前应先清理基层，如墙面上有石灰膏、乳胶漆、壁纸等装饰物，或地面上有污物，一定要清理干净，否则水泥砂浆与基层粘结不牢；另外，如果墙体自身有裂缝，应做妥善处理后才可贴砖，以免日后基本结构裂缝变大导致墙面砖开裂或脱落；还有，对于平整度或垂直度差距太大的地面、墙面，还要用水泥砂浆进行找平处理。铺前还要比较瓷砖的色彩差异。

其次，墙面砖要充分浸水。因为墙面砖有着较高的含水率，在粘贴时必须考虑到它的这一特性。贴砖前基层应充分浇水湿润，瓷砖也应在水中浸泡至少20分钟后充分阴干方可使用。否则，砂浆中的水分被干燥的基层和瓷砖迅速吸收而快速凝结，会影响其粘结牢度。否则，墙砖会从水泥里吸收水分，使水泥无法起到粘贴剂的作用。

铺地砖要用水泥砂浆先将地面铺平，将未涂水泥的地砖铺在地面，敲平后，将水泥浆涂满地砖，铺于地面，四块砖的对角位置齐平。而铺设的顺序也有讲究。贴地面砖应由内向外贴，如地面有坡度或有地漏，应注意按排水方向找坡；墙砖应从下向上铺贴，为美观起见，最底层的砖应后贴。墙砖贴完后再压地砖。另外，一面墙不能一次贴到顶，以防瓷砖自重较大，引起塌落。铺完地砖短时间内不要踩踏。

为迎合追求新潮的消费者，市场上出现了一些新的工艺方法，例如瓷砖黏着剂、多彩填缝剂、留缝铺装等。瓷砖黏着剂(也叫干贴法)，瓷砖不需预先浸水基面不需打湿，只要铺装的基础条件较好就可以，使作业状况得到极大改善。

第二篇：高中数列知识大总结(绝对全)

第六章数列

二、重难点击

本章重点：数列的概念，等差数列，等比数列的定义，通项公式和前n项和公式及运用，等差数列、等比数列的有关性质。注重提炼一些重要的思想和方法，如：观察法、累加法、累乘法、待定系数法、倒序相加求和法、错位相减求和法、裂项相消求和法、函数与方程思想、分类与讨论思想、化归与转化思想等。

知识网络

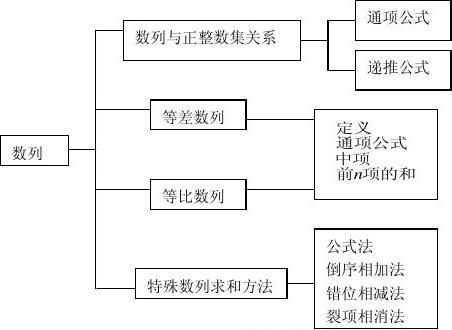
高中数列知识大总结绝对全

四、数列通项an与前n项和Sn的关系

1．Sn?a1?a2?a3???an??ai

i?1

2．a?S1n?1

n???Sn?Sn?1n?2

课前热身

3．数列?an?的通项公式为 an?3n2?28n,则数列各项中最小项是( B )

A．第４项 B．第５项 C．第６项 D．第７项

4．已知数列?an?是递增数列，其通项公式为an?n2??n,则实数?的取值范围是(?3,??)

5．数列?a2??2

n?的前n项和Sn?n?4n?1,，则an??n?1

?2n?5n?2

题型一归纳、猜想法求数列通项

【例1】根据下列数列的前几项，分别写出它们的一个通项公式

⑴7，77，777，7777，?

⑶1，3，3，5，5，7，7，9，9? 解析：⑴将数列变形为7777?(10?1),(102?1),(103?1)，?,(10n?1) 9999

⑶将已知数列变为1+0，2+1，3+0，4+1，5+0，6+1，7+0，8+1，9+0，?。可得数列的通项公式为

?n?1?(?1)n

an2

点拨：本例的求解关键是通过分析、比较、联想、归纳、转换获得项与项数的一般规律，从而求得通项。题型二应用a?S1(n?1)

n???Sn?Sn?1(n?2)求数列通项

例2．已知数列?an?的前n项和Sn，分别求其通项公式.

⑴Sn?3n?2

解析：⑴当n?1时,a1?S1

1?3?2?1，

当n?2时,an?Sn

n?Sn?1?(3?2)?(3n?1?2)

?2?3n?1

又a?1不适合上式，故a?1(n?1)

1n???2?3n?1(n?2)

三、利用递推关系求数列的通项

【例3】根据下列各个数列?an?的首项和递推关系，求其通项公式 ⑴a11

1?2,an?1?an?4n2?1 解析：⑴因为a1

n?1?an?4n2?1，所以

aa1111

n?1?n?4n2?1?2(2n?1?2n?1) 所以a?a111

21?2(1?3)

a111

3?a2?2(3?5)

a111

4?a3?2(5?7)

?，?，

an?an?1?111(?) 22n?32n?1

以上(n?1)个式相加得 11(1?) 22n?1

14n?3?即：an?1? 4n?24n?2 an?a1?

点拨：在递推关系中若an?1?an?f(n),求an用累加法，若an?1?f(n),求an用累乘法，若anan?1?pan?q，求an用待定系数法或迭代法。

课外练习

3设an?111?????，(n?N)，则an?1与an的大小关系是( C ) n?1n?22n?1

A．an?1

C．an?1?an B．an?1?an ?an D．不能确定

解：因为

111??2n?22n?3n?1 11???02n?32n?2an?1?an?

所以an?1

二、填空题

5．已知数列

7．已知数列?an，选Ｃ． ?则an???an?的前n项和Sn?n2?4n?1，?2,(n?1) ?2n?5,(n?2)?an?的通项n?

y?x?98

x?9998n?99?1?（n?N），则数列??an?的前30项中最大项和最小项分别是a10，a9 解：构造函数99?98

x?99 由函数性质可知，函数在(??99)上递减，且y?1 函数在(

上递增且y?1 99，＋?）3

又?(9，10）

?a10?a11?a12???a30?1?a1?a2??三、解答题

?a9

?a10最大，a9最小

6.2等差数列

知识要点

2．递推关系与通项公式

递推关系：an?1?an?d通项公式：an?a1?(n?1)d推广：an?am?(n?m)d变式：a1?an?(n?1)d;

an?a1

n?1d?an

?am

n?m

特征：an?dn?(a1?d),

即：a,m为常数）

n?f(n)?kn?m,(kan?kn?m，（k,m为常数)是数列?an?成

等差数列的充要条件。３．等差中项：

若a,b,c成等差数列，则b称a与c的等差中项，且b?

a?c

；a,b,c成等差数列是2b?a?c的充要条件。４．前n项和公式

Snn?

(a1?an)2

； Sn(n?1)d

n?na1?2

特征：Sdn?

2n2?(ad

1?2)n,即S2n?f(n)?An?Bn

Sn?An2

?Bn

(A,B为常数)

是数列

?an?成等差数列的充要条件。

5．等差数列

?an?的基本性质(其中m,n,p,q?N?)

⑴若m?n?

p?q，则am?an?ap?aq反

之，不成立。 ⑵an

?am?(n?m)d ⑶2an

?an?m?an?m

⑷Sn,S2n

?Sn,S3n?S2n仍成等差数列。

６．判断或证明一个数列是等差数列的方法：

①定义法：

an?1?an?d(常数）（n?N?）??an?是等

差数列

②中项法：

2an?1?an?an?2

（n?N?)??an?是等差数

列

③通项公式法：

an?kn?b

(k,b为常数)??an?是等差数

列

④前n项和公式法：

Sn?An2?Bn

(A,B为常数)??an?是等

差数列课前热身 2．等差数列

?an?中，

a4?a6?a8?a10?a12?120,则a1

9?3

a11的值为(C)

A．14 B．15 C．16 D．17

解 a11

9?3a11?a9?3

(a9?2d)

?23(a22120

9?d)?3a8?3?5

?16

。 3．等差数列

?an?中，a1?0，S9?S12，则前

或11项的和最大。解：?S9

?S12，S12?S9?0

?a10?a11?a12?0，?3a11?0，?a

11?0，又a1?0

∴

?an?为递减等差数列∴S10?S11为最大。

4．已知等差数列

?an?的前10项和为100，前100项和

为10，则前110项和为－110 解：∵

S10，S20?S10，S30?S20，?，S110?S100，?

成等差数列，公差为D其首项为

S10?100，前10项的和为S100?10 ?100?10?10?9

?D?10，?D??22又S110

?S100?S10?10D

?S110?100?10?10（??22）??110

y?50n?98??

?n(n?1)??12n?2?4?

??2n2

?40n?98

??2(n?10)2?102所以当n?10时，ymax?102

６．设等差数列

?an?的前n项和为Sn，已知

a3?12，S12?0，S13?0

①求出公差d的范围，

②指出S1，S2，

?，S12中哪一个值最大，并说明理由。

dan?f(n)nanSn?an?"n?2"

解：①S12?6(a1?a12)?6(a3?a10)

?6(2a3?7d)?0

?24?7d?0?d??

247

又S13(a1?a13)13?

2?13

2(a3?a11) ?13

(2a3?8d)?0?24?8d?0?d??3

从而?247

?d??3

②

?S12?6(a6?a7)?0

S13?13a7?0

?a7?0，a6?0

?S6最大。

课外练习一、选择题 1．已知

?an?数列是等差数列，a10?10，其前

项的和S10

?70，则其公差d等于( D )

A．?23

B．?1

3 C1

D23

2．已

知

等

差

数

列

?an?

中，

a7?a9??16，a4?1，则a12等于（ A ）

A．15 B．30 C．31 D．64

解：?a7?a9?a4?a12

?a12?15

二、填空题 3．设

Sn为等差数列?an?的前n项和，

S4?14，S10?S7?30，则S9=54

4．已知等差数列

?an?的前n项和为Sn

，若

S12?21，则a2?a5?a8?a11?

．设F是椭圆x2y2

57?6

?1的右焦点，且椭圆上至

少有21个不同点

Pi(i?1,2,?)使P1FP2FP

3F,?

组成公差为d的等差数列，则d的取值范围为

????110，0???????01?10??

解：椭圆的焦点F到椭圆上的点最大、最小距离分别为(

7?1)7?1）

，由题意得： ?1）?（n?1)d?7?1?d?

n?1

?n?1?20

?d?1

10，又d?0

??110?d?0或0?d?

110三、解答题 6．等差数列

?an?的前n项和记为Sn

，已知

a10?30，a20?50

①求通项an；②若Sn=242，求n 解：an

?a1?(n?1)d

a10?30，a20?50

解方程组??a1

?9d?30

?a1

?19d?50 ???a1?12?d?2

?an?2n?10由Sn?na1?

n(n?1)d

，Sn=242 ?12n?

n(n?1)

?2?242

解得n?11或n??22(舍去）

7．甲、乙两物体分别从相距70m的两处同时相向运

动，甲第一分钟走2m，以后每分钟比前一分钟多

走1m，乙每分钟走5m，①甲、乙开始运动后几分钟相遇？②如果甲乙到对方起点后立即折返，甲继续每分钟比前一分钟多走1m，乙继续每分钟走5m，那么，开始运动几分钟后第二次相遇？解：①设n分钟后第一次相遇，依题意有：

2n?

n(n?1)

?5n?70

解得n?7，n??20(舍去）故第一次相遇是在开始运动后7分钟。 ②设n分钟后第二次相遇，则：

2n?

n(n?1)

?5n?3?70

解得n?15，n??28(舍去）故第二次相遇是在开始运动后15分钟 10．已知数列

?an?

中，

a1?3，前n和

Sn?

(n?1)(an?1)?1 ①求证：数列?an?是等差数列

②求数列

?an?的通项公式

③设数列?

a?的前n项和为Tn，是否存在实

?nan?1?

数M，使得Tn

?M对一切正整数n都成立？若存

在，求M的最小值，若不存在，试说明理由。解：①∵S1

(n?1)(an?1)?1 ?Sn?1?1

(n?2)(an?1?1)?1?an?1?Sn?1?Sn

?(n?2)(an?1?1)?(n?1)(an?1)?

整理得，nan?1?(n?1)an?1

?(n?1)an?2?(n?2)an?1?1?(n?1)an?2?nan?1?(n?2)an?1?(n?1)an

?2(n?1)an?1?(n?1)(an?2?an)?2an?1?an?2?a

∴数列

?an?为等差数列。

②a1?3，nan?1?(n?1)an?1

?a2?2a1?1?5?a2?a1?2

?an?的公差为2即等差数列

?an?a1?(n?1)d?3?(n?1)?2?2n?1

③?

anan?1(2n?1)(2n?3)

1?11?

???

2?2n?12n?3?

1111111

?Tn?(???????)

235572n?12n?3 111?(?)232n?3

又当n?N?时，Tn?

要使得Tn

?M对一切正整数n恒成立，只要M≥

，所以存在实数M使得Tn?M对一切正整数n 6

都成立，M的最小值为

1。 6

6.3等比数列

知识要点

1．定义：如果一个数列从第二项起，每一项与它的前一项的比等于同一个常数，那么这个数列叫做等比数列，这个常数叫做等比数列的公比，记为

5．等比数列的基本性质，(其中m,n,p,q?N ①

)

若m?n?p?q，则am?an?ap?aq反之

q，（q?0)。

2．递推关系与通项公式

不真！ ②q

n?m

递推关系：an?1?qan通项公式：an?a1?qn?1 推广：an?am?qn?m

3．等比中项：若三个数a,b,c成等比数列，则称b为

③

an2

，an?an?m?an?m(n?N?) am

?an?为等比数列，则下标成等差数列的对应项

q??1时，Sn，S2n?Sn，S3n?S2n，?仍

成等比数列。 ④

a与c的等比中项，且为b??ac，注：b?ac

是成等比数列的必要而不充分条件。 4．前n项和公式

成等比数列。

6．等比数列与等比数列的转化 ①

?an?是等差数列??ca?

(c?0，c?1)是

(q?1)?na1

Sn??a1(1?qn)a1?anq

?1?q?1?q

等比数列；

(q?1)

②

?an?

是正项等比数列

??logcan?

(c?0，c?1)是等差数列；

③

?an?既是等差数列又是等比数列??an?是各

项不为零的常数列。 7．等比数列的判定法 ①定义法：

an?1

a?q（常数）??an?为等比数列；

②中项法：a2

n?1?an?an?2

(an?0)??an?为

等比数列；

③通项公式法：an

?k?qn(k,q为常数）??an?

为等比数列；④前

项和法：

Sn?k(1?qn)（k,q为常数）??an?为等比数

列。

1．设f(n)?2?2

?27?210???2

3n?10

(n?N?)，则f(n)等于（D）

A27(8n?1)B27(8n?1?1)

C2(8n?3?1)D2(8n?477

?1)2．已知数列

?an?

是等比数列，且

Sm?10，S2m?30，则S3m?猜想：

?b1n?是等比数列，公比为2。

证明如下：∵bn?a111

2n?1?4?2a2n?4

1(a11

2n?1?) 24?4

?12(a11

2n?1?4)?2

即：

bn?1b?1，∴?b1

n?是首项为a?n2

4，公比

为1

的等比数列。

二、性质运用

例2：⑴在等比数列

?an?

中，

a1?a6?33，a3a4?32，an?an?1

①求an， ②若Tn

?lga1?lga2???lgan,求Tn

⑵在等比数列

?an?中，若a15

?0，则有等式

a1?a2???an?a1?a2???a29?n

(n?29，n?N?)成立，类比上述性质，相应的

在等比数列?bn?中，

若b19?1则有等式成立。

解：⑴①由等比数列的性质可知：

a1?a6?a3?a4?32又a1?a6?33，a1?a6

解得a1?32，a6

所以

a6a?132，即q5?132，?q?1

所以a(1

n?32?)n?1?26?n

②由等比数列的性质可知，

?lgan?是等差数

列，因为

lgan?lg26?n?(6?n)lg2，lga1?5lg2所以T(lga1?lgan)nn(11?n)

n?2?2

lg2

⑵由题设可知，如果

am?0在等差数列中有

a1?a2???an?a1?a2???a2m?1?n (n?2m?1，n?N?)成立，我们知道，如果

若m?n?p?q，则am?an?ap?aq，而对于

等

比

数

列

?bn?

，则有

若m?n?p?q，则am?an?ap?aq所以可以得

出结论，若

bm?1，则有b1b2?bn?b1b2?b2m?1?n(n?2m?1，n?N?)成立，在本题中

则有b1b2?bn?b1b2?b37?n(n?37，n?N?)

点拨：历年高考对性质考查较多，主要是利用“等积性”，题目“小而巧”且背景不断更新，要熟练掌握。典例精析

一、错位相减法求和例1：求和：Sn?12a?3n

a2?a3???a

n 解：⑴

a?1时，Sn(n?1)

n?1?2?3??n?

⑵a?1

时，因为a?0 S1n?a?23aa???n

2?3an ① 1aS12n?1n?a2?a3???an?n

an?1

②

由①－②得：

(1?1a)S111nn?a?a2???an?a

n?1

1(1?1?a

an)

1?1?nan?1a

所以Sa(an?1)?n(a?1)

an(a?1)2

综上所述，

?n(n(a?1)S???1)??n

2n?a(a?1)?n(a?1)??

an(a?1)2a?1)

点拨：①若数列

?an?是等差数列，?bn?是等比数列，则求数列

?an?bn?的前n项和时，可采用错位

相减法；

②当等比数列公比为字母时，应对字母是否为

1进行讨论；

③当将Sn与qSn相减合并同类项时，注意错

位及未合并项的正负号。

二、裂项相消法求和例

：

数

列

?an?

满足

=8，

a4?2，且an?2?2an?1?an?0 （n?N?）

①求数列

?an?的通项公式；

则d?

a4?a1

4?1

??2

所以，an=8＋（n－1）×（－2）＝―10－2n

bn?1n(14?a)?

n2n(n?2)

111

4(n?n?2)所以

②Tn?b1?b2???bn

1?4??(11?13)?(12?14)???(11?

n?n?2)???11114(1?2?n?1?n?2)?38?14(n?1)?1m4(n?2)?32 对一切n?N?

恒成立。

?m?12?

8n?1?8n?2

对一切n?N?恒成立。对n?N?，（12?88

n?1?n?2

)min?

12?8816故

1?1?1?2?

3所以m?

m的最大整数值为5。

点拨：①若数列

?an?

的通项能转化为

f(n?1)?f(n)的形式，常采用裂项相消法求和。

②使用裂项消法求和时，要注意正负项相消时，

消去了哪些项，保留了哪些项。三、奇偶分析法求和例3：设二次函数f(x)?x2?x，当x??n，n?1?

1．在等差数列

?an?中，a1=1，前n项和Sn满足

S2nS?4n?2

，n?1，2，? nn ①求数列?an?的通项公式

②记ban?anpn(p?0)，求数列?bn?的前n项和Tn。

解：①设数列

?an?

的公差为d，由

S2nS?4n?2

n?1，n?1，2，? n得

a1?a2

a?3，所以a2?21即d?a2?a1?1又

4n?2n?1?S2n

Sn(an?nd?a1)2n

(an?a1)n

2(an?n?1)an?1

所以an=n ②由bn

?aanpn(p?0)，有bn?npn

所以Tn

?p?2p2?3p3???npn ①

当p?1时，Tn(n?1)

当p?1时，

pT3n?p2?2p???(n?1)pn?npn?1②

①－②得

(1?p)T2n?p?p???pn?npn?1

p(1?pn?)

?npn?1

1?p

所以Tp(1?pn)npn?1

n?(1?p)2

?1?p

n(n(p?1)即：T??1)??p(1?pn

n?)npn?1???

(1?p)2?1?p(p?1)

课外练习１．数列

?an?

的前

项和为

Sn，若

an?

n(n?1)

，则S5等于（ B ）

A．1

B．

516

C．

6D．1

解：因为a?111

nn(n?1)?n?

n?1

所以S111111

5?(1?2)?(2?3)???(5?6)

?56

４．f(x)的定义域为R，且f(x)是以2为周期的周期函数，数列

?an?是首项为a

(a?N?)，公差为

1的等差数列，那么f(a1)?f(a2)???f(a10)的值为（ C ）

A．－1 B．1 C．0 D．10a 解：因为函数f(x)的定义域为R，且f(x)是

以2为周期的周期函数，所以

f(0）?0，且f(x?2)?f(x)

又数列

?an?是首项为a，公差为1的等差数列

所以an?a?n?1，又a?N?f(a?f(a)（n为奇数）

n)??

?f(a?1)（n为偶数）

所以f(a1)?f(a2)???f(a10)

?5f(a)?5f(a?1)

?5?f(0)?f(1)??5f(1)又f(?1)f(?1?2)?f(1)所以?f(1)?f(1)

即f(1)?0

故原式=0，选C。二、填空题５．设等比数列

?an?的公比与前n项和分别为q和

Sq≠1，S，则S

20n，且10?81?q

10?

a1(1?q10)

1?2?8

?S201?q10?a1(1?q20)(1?q10）(1?q)

?8方法二、S20?S10?a11?a12???a20

?S1010?qS10?S10(1?q10)所以

S20

1?q10

?S10?8

6．数列

?an?满足an?

12nn?1?n?2???n?1

，又b2n?

，则数列

?abn?的前n项和为

nan?1

n?1

解：an?

1n?1(1?2???n)?n2 b?28naa?n(n?1)= 8(11n?n?1

） nn?1所以b1?b?8?12???b1

111??(1?2)?(2?3)???(?n?n?1)?

?8?

1??1??8n?

n?1???n?1

数列1

11xxxxxxxxxxxx444

，?的前100项13

9。（n?N?

） 11

７．的和为

典例精析

一、函数与数列的综合问题

例1：已知f(x)?logax(a?0且a?1)，

设f(a1)，f(a2)，?，f(an)(n?N?)

是首项为4，公差为2的等差数列。

①设a是常数，求证：

②若bn?an?成等差数列； ?anf(an)，?bn?的前n项和是Sn，当a?2时，求Sn

解：①f(an)?4?(n?1)?2?2n?2，

即logaan?2n?2，所以an?a2n?2

ana2n?2

所以?2n?a2(n?2)为定值 an?1a

所以?an?为等比数列。

②bn?anf(an)

?a2n?2logaa2n?2?(2n?2)a2n?2

当a?2时，

bn?(2n?2)?(2)2n?2?(n?1)?2n?2

Sn?2?23?3?24?4?25???(n?1)?2n?2

2Sn?2?24?3?25???n?2n?2?(n?1)?2n?3点拨：本例是数列与函数综合的基本题型之一，特两式相减得

?Sn?2?23?24?25???2n?2?(n?1)?2n?3

24(1?2n?1)?16??(n?1)?2n?3

1?2

所以Sn?n?2n?3

征是以函数为载体构建数列的递推关系，通过由函数的解析式获知数列的通项公式，从而问题得到求解。１．已知正项数列

①求证：数列?an?的前n项和为Sn，?an?是等差数列； 1Sn是与(an?1)2的等比中项， 4

②若bn?an，数列?bn?的前n项和为Tn，求Tn n2 ③在②的条件下，是否存在常数?，使得数列??Tn??? ?为等比数列？若存在，试求出?；若不存在，说明理由。

?an?2?

解：①1Sn是与(an?1)2的等比中项， 4

选校网专业大全历年分数线上万张大学图片大学视频院校库 12

1(an?1)2

1当n?1时，a1?(a1?1)2，?a1?14

1当n?2时，S?(an?1?1)2 n?14

所以an?Sn?Sn?1所以Sn?

122(an?an?1?2an?2an?1)4

即(an?an?1)(an?an?1?2)?0?

因为an?0，所以an?an?1?2?0

即：an?an?1?2

所以数列?an?是等差数列。 2n?3 n2 ②Tn?3?

Tn??2n?31 ?(3???)?an?22n?32n

3??1?n 2n?32 ?

所以当且仅当3+?=0，即?=－3时，数列 ?Tn?????为等比数列。

?an?2?

２．已知在正项数列?an?中，a1=2，且

22在双曲线y?x?1上， An(anan?1）

数列?bn?中，

点（bn，Tn）在直线y??

等比数列。③若Cn1x?1上，其中Tn是数列?bn?的前n项和，①求数列?an?的通项公式；②求证：数列?bn?是2?an?bn，求证：Cn?1?Cn。

22在y?x?1上知， anan?1）解：①由已知带点An(

an?1－an＝１，所以数列?an?是以2为首项，以1为公差的等差数列。

?a1?(n?1)d?n?1

1x?1上， 2所以an②因为点（bn,Tn）在直线y??

选校网专业大全历年分数线上万张大学图片大学视频院校库 13

1所以Tn??bn?121所以Tn?1??bn?1?1 2两式相减得：

11bn?Tn?Tn?1??bn?bn?122

1所以bn?bn?1，312令n?1得b1??b1?1，所以b1?232 所以?bn?是一个以为首项，31以为公比的等比数列。3212所以bn??()n?1?n333

③Cn?an?bn?(n?1)?2 n3

所以Cn?1?Cn?(n?2)?

23n?1?(n?1)23n ?2

3n?1?(?2n?1)?0

所以Cn?1?Cn

一、选择题

2n{a}a?0,n?1,2,?a?a?2(n?3)1.（2009广东卷理）已知等比数列n满足n，且52n?5，则当n?1时，

log??lo2gan??2a1?log2a3?21

222n(2n?1)(n?1)(n?1)nA. B. C. D.

a?a?【解析】由5n222nn2na?0log2a1?log2a3????? a?2a?2?2(n?3)5得n，n，则n，

log2a2n?1?1?3?????(2n?1)?n2

，选C.

答案 C

S9S6

SaSS2.（2009辽宁卷理）设等比数列{ n}的前n 项和为n ，若 3=3 ，则 6 =

A. 2 B. 3 C. 3 D.3

S6(1?q3)S3?SS3【解析】设公比为q ,则3＝1＋q3＝3 ? q3＝2

选校网专业大全历年分数线上万张大学图片大学视频院校库 14

于是【答案】B

S91?q3?q61?2?47???S61?q31?23

?an

?,当an为偶数时，an?1??2

?3an?1,当an为奇数时。a＝1an?a1＝m??14.(2009湖北卷理)已知数列满足：（m为正整数），若6，则m所有

可能的取值为__________。

答案 4 5 32

a1amam

解析（1）若a1

?m为偶数，则2为偶, 故2?2 a3?22?

4 ma?m??????amm

①当4仍为偶数时，486?32?1?m 故32?32

mm?14a?3

为奇数时，4?3a3?1m?1??????a②当46?4 3

m?1?1故4得m=4。

a3m?1

（2）若

a1?m为奇数，则a2?3a1?1?3m?1为偶数，故

2必为偶数

??????a3m?1

3m?16?

16，所以16=1可得m=5

16.（2009陕西卷文）设等差数列?an?的前n项和为sn,若a6?s3?12,则an? 解析:由

a6?s3?12可得?an?的公差d=2,首项a1=2,故易得an?2n.

答案:2n

?alim

S17.(2009陕西卷理)设等差数列的前n项和为Sn

?n?n,若a6?S3?12,则n??n2 解析：??a6?12?a1?5d?12?a1?2Sn?1Snn??s?????Sn?1)?n??lim?lim1

n?n(?13

?12?a1?d?12?d?2n2nn??n2n??n

答案：1

22.（2009全国卷Ⅰ理）在数列{aaa1n?1

n}中，

1?1,n?1?(1?n)an?2n

选校网专业大全历年分数线上万张大学图片大学视频院校库

（I）设n?a

n，求数列{bn}的通项公式

（II）求数列{an}的前n项和Sn

an?1?an?11

分析：（I）由已知有n?1n2n?bn?1?bn?2n

利用累差迭加即可求出数列{bn}b2?1

的通项公式: n?2n?1(n?N*)

a?2n?n

（II）由（I）知n2n?1,

?Sn=?(2k?knn)?k?12k?1?(2k)??kk?1k?1k?12

?nn

(2k)?n(n?1)

而k?1,又?kkk?12?1是一个典型的错位相减法模型，

易得?nkn?k?1?4?2k?122n?1(n?1)?n?2

?Sn=n2n?1?4

23.（2009北京理）已知数集A??a1,a2,?an??1?a1?a2??an,n?2?具有性质P；对任意的

i,j?1?i?j?n?，aiaj与ai两数中至少有一个属于A.

（Ⅰ）分别判断数集?1,3,4?与?1,2,3,6?是否具有性质P，并说明理由；

a1?a2???an

（Ⅱ）证明：a1?1?1?1?1?an

，且a1?a2???an；

（Ⅲ）证明：当n?5时，a1,a2,a3,a4,a5成等比数列. 【解析】本题主要考查集合、等比数列的性质，考查运算能力、推理论证能力、分分类讨论等数学思想方法．本题是数列与不等式的综合题，属于较难层次题.

（Ⅰ）由于3?4与3均不属于数集?1,3,4?，∴该数集不具有性质P.

1?2,1?3,1?6,2?3,661236

由于2,3,1,2,3,6都属于数集?1,2,3,6?，

∴该数集具有性质P.

选校网专业大全历年分数线上万张大学图片大学视频院校库 16

A??a1,a2,?an?aaa（Ⅱ）∵具有性质P，∴nn与n中至少有一个属于A，

由于1?a1?a2???an，∴anan?an，故anan?A.

1?an?Aa?1. an，∴1从而

∵1?a1?a2???an， ∴akan?an，故akan?A?k?2,3,?,n?. an?A?k?1,2,3,?,n?a由A具有性质P可知k.

anaaa?n???n?n

aan?1a2a1，又∵n

anaaa?1,n?a2,?n?an?1,n?anaan?1a2a1∴n，

anaaa?n???n?n?a1?a2???an?1?anaan?1a2a1从而n，

a1?a2???an?an?1?1?1a?a2???an∴1.

a5a?a2,5?a32a?aa?aaan?5524343（Ⅲ）由（Ⅱ）知，当时，有，即，

∵1?a1?a2???a5，∴a3a4?a2a4?a5，∴a3a4?A， a4?Aa由A具有性质P可知3.

a3a4a3a4a3??A1??a??a222aa?aaaaaa3，得2322 24，且，∴3，

a5a4a3a2????a2a,a,a,a,aaaa3a2a1∴4，即12345是首项为1，公比为2成等比数列.

25（2009江苏卷）对于正整数n≥2，用

组数，其中Tn表示关于x的一元二次方程x2?2ax?b?0有实数根的有序数组(a,b)的a,b??1,2,?,n?（a和b可以相等）；对于随机选取的a,b??1,2,?,n?（a和b可以相等），记Pn为关于x的一元二次方程x2?2ax?b?0有实数根的概率。

选校网专业大全历年分数线上万张大学图片大学视频院校库 17

（

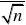
高中数列知识大总结绝对全

1）求Tn2和Pn2；

（2）求证：对任意正整数n≥2

高中数列知识大总结绝对全

，有Pn?1?.

【解析】 [必做题]本小题主要考查概率的基本知识和记数原理，考查探究能力。满分10分。

29.（2009江西卷理）各项均为正数的数列{an}，a1?a,a2?b，且对满足m?n?p?q的正整数m,n,p,q都有

ap?aqam?an?.(1?am)(1?an)(1?ap)(1?aq)

14a?,b?25时，求通项an; （1）当

（2）证明：对任意a，存在与a有关的常数?，使得对于每个正整数n，都有??an??.

解：（1）由ap?aqam?an?(1?am)(1?an)(1?ap)(1?aq)得

a1?ana2?an?1?.a1?1,a2?4

(1?a1)(1?an)(1?a2)(1?an?1)将25代入化简得 an?

2an?1?1.an?1?2

1?an11?an?1??,1?an31?an?1 所以

选校网专业大全历年分数线上万张大学图片大学视频院校库 18

{1?an故数列1?an为等比数列，从而

1?ann

1?a?13

n,a

n3即n??1

3n?1.

a3n?1

可验证，n?3n?1满足题设条件.

am?an(2) 由题设(1?aaba1?ana?an

n?1?)?(1?a)(1?a.

m)(1?n)的值仅与m?n有关,记为bm?n,则(1?a1)(1?ann) f(x)?a?x

考察函数 (1?a)(1?x)(x?0)

,则在定义域上有

??1a?1

?1?a,

f(x)?g(a)???1

?2,a?1

??a

?1?a,0?a?1

故对n?N*， bn?1?g(a)恒成立. b2an

2n?

又 (1?a

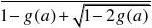
高中数列知识大总结绝对全

2?g(a)

n),

0?g

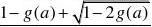
高中数列知识大总结绝对全

(a)?1

注意到

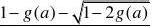
高中数列知识大总结绝对全

2,解上式得

??an?

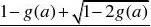
高中数列知识大总结绝对全

??1

取?a

,即有 ?n??.

S??a?(1)n?1?

30. (2009湖北卷理)已知数列?an?的前n项和nn22

（n为正整数）。

（Ⅰ）令bn?2nan，求证数列?bn?是等差数列，并求数列?an?的通项公式；

c?1

na5n

(Ⅱ）令n?nn，Tn?c1?c2?........?cn试比较Tn与2n?1的大小，并予以证明。

选校网专业大全历年分数线上万张大学图片大学视频院校库 19

S1?1

解（I）在n??an?(2)n?2

中，令n=1，可得S1??a?2?aa1

n?11，即1?2

S1?2?S1

当n?2时，n?1??an?1?()n?2，?an?Snn?1??an?an?1?(2)n?1

2，

?2a1?1

n?an?1?()n,即2nan?1

2n?2an?1?1

?bn?2nan,?bn?bn?1?1,即当n?2时，bn?bn?1?1. 又b1?2a1?1,?数列?bn?是首项和公差均为1的等差数列.

于是n?1?(n?1)?1?n?2nan,?an?n

2n.

c?n?1a1)(1)n

(II)由（I）得nnn?(n?2，所以

T?1?3?(1)2?4?(1)3?K?(n?1)(1

n?2)n

2222

2)2?3?(1

2)3?4?(11

n?2?(2)4?K?(n?1)(2)n?1

1T1)2?(1)3?K?(1)n1

由①-②得2n?1?(222?(n?1)(2)n?1

1[1?(1)n?1]

?1??(n?1)(1)n?13n?3

1?2?2?2n?1

?T?3?n?3

n2n

T5nn?35n(n?3)(2n?2n

2n?1?3??1)

n?2n?2n?1?2n(2n?1)

于是确定n与5n

2n?1的大小关系等价于比较2n与2n?1的大小

由2?2?1?1;22?2?2?1;23?2?3?1;24?2?4?1;25?2?5;K 可猜想当n?3时，2n?2n?1.证明如下：

证法1：（1）当n=3时，由上验算显示成立。

（2）假设n?k?1时2k?1?2g2k?2(2k?1)?4k?2?2(k?1)?1?(2k?1)?2(k?1)?1

选校网专业大全历年分数线上万张大学图片大学视频院校库 20

所以当n?k?1时猜想也成立

综合（1）（2）可知，对一切n?3的正整数，都有2?2n?1.

证法2：当n?3时

012n?1n01n?1n2n?(1?1)n?Cn?Cn?Cn?K?Cn?Cn?Cn?Cn?Cn?Cn?2n?2?2n?1 n

综上所述，当n?1,2时Tn?5n5nTn?2n?1，当n?3时2n?1

31.（2009四川卷文）设数列

（I）求数列a?5Sn?1成立，?an?的前n项和为Sn，对任意的正整数n，都有n记bn?4?an(n?N*)1?an。 ?an?与数列?bn?的通项公式；

?bn?的前n项和为Rn，是否存在正整数k，使得Rn?4k成立？若存在，找出一个正整数k；若不存在，

Tn?3

2；（II）设数列请说明理由；（III）记cn?b2n?b2n?1(n?N)，设数列?cn?的前n项和为Tn，求证：对任意正整数n都有*

解（I）当n?1时，

又a1?5S1?1,?a1??14 ?an?5Sn?1,an?1?5Sn?1?1

an?11??an4 11q??4，公比为4的等比数列， ?an?1?an?5an?1,即∴数列?an?是首项为a1??14?(?)n

(n?N*)bn?1an?(?)n1?(?)n

4，4∴ ?????????????3分

（II）不存在正整数k，使得Rn?4k成立。

14?(?)n5?4?bn?nn(?4)?11?(?)4证明：由（I）知

选校网专业大全历年分数线上万张大学图片大学视频院校库 21

?bb5552015?16k?40

2k?1?2k?8?(?4)2k?1?1?(?4)2k?1?8?16k?1?16k?4?8?(16k?1)(16k?4)?8.

∴当n为偶数时，设n?2m(m?N?) ∴Rn?(b1?b2)?(b3?b4)???(b2m?1?b2m)?8m?4n

当n为奇数时，设n?2m?1(m?N?)

∴Rn?(b1?b2)?(b3?b4)???(b2m?3?b2m?2)?b2m?1?8(m?1)?4?8m?4?4n ∴对于一切的正整数n，都有Rn?4k ∴不存在正整数k，使得Rn?4k成立。 ?????????????8分

n?4?

（III）由(?4)n?1得 c5515?16n15?16n15?16n15n?b2n?1?b2n?42n?1?42n?1?1?(16n?1)(16n?4)?(16n)2?3?16n?4?(16n)2?16nb1?3,b13

2?3,?c4

2?3， T3当n?1时，1?2，

当n?2时，

1[1?(1)n?2

T4?25?(1114]

n?2?3???n)?3?25?31616161?1

?42693

3?25???

1?482

16 32.（2009湖南卷文）对于数列{un},若存在常数M＞0,对任意的n?N*，恒有 un?1?un?un?un?1???u2?u1?M, 则称数列{un}为B?数列.

（Ⅰ）首项为1，公比为2的等比数列是否为B-数列？请说明理由;

（Ⅱ）设Sn是数列{xn}的前n项和.给出下列两组判断：

选校网专业大全历年分数线上万张大学图片大学视频院校库又22

A组：①数列{xn}是B-数列, ②数列{xn}不是B-数列;

B组：③数列{Sn}是B-数列, ④数列{Sn}不是B-数列.

请以其中一组中的一个论断为条件，另一组中的一个论断为结论组成一个命题. 判断所给命题的真假，并证明你的结论；

(Ⅲ)若数列{an}是B-数列，证明：数列{a2

n}也是B-数列。

: （Ⅰ）设满足题设的等比数列为n,则n?(?)n?1

解{a}2.于是

a1131

n?an?1?(?2)n?1?(?2)n?2?2?(2)n?2,n?2.

|an?1?an|?|an?an?1|???|a2?a1|

3??1121n-1?1n?

=2??1?2?（2）???（2）??3??1?（

=??2）???3.

所以首项为1，公比为2的等比数列是B-数列 .

（Ⅱ）命题1：若数列{xn}是B-数列，则数列{Sn}是B-数列.此命题为假命题. 事实上设xn=1，n?N*，易知数列{xn}是B-数列，但Sn=n，

|Sn?1?Sn|?|Sn?Sn?1|???|S2?S1|?n.

由n的任意性知，数列{Sn}不是B-数列。

命题2：若数列{Sn}是B-数列，则数列{xn}不是B-数列。此命题为真命题。事实上，因为数列{Sn}是B-数列，所以存在正数M，对任意的n?N*，有 |Sn?1?Sn|?|Sn?Sn?1|???|S2?S1|?M,

即|xn?1|?|xn|???|x2|?M.于是xn?1?xn?xn?xn?1???x2?x1 ?xn?1?2xn?2xn?1???2x2?x1?2M?x1,

所以数列{xn}是B-数列。

（注：按题中要求组成其它命题解答时，仿上述解法）

(Ⅲ)若数列?an?是B-数列，则存在正数M，对任意的n?N?,有

选校网专业大全历年分数线上万张大学图片大学视频院校库 23

an?1?an?an?an?1???a2?a1?M.

因为an?an?an?1?an?1?an?2???a2?a1?a1

?an?an?1?an?1?an?2???a2?a1?a1?M?a1.

记K?M?a1a22，则有n?1?an?(an?1?an)(an?1?an)

?(an?1?an)an?1?an?2Kan?1?an.

a222?a222

因此n?1?an?ann?1?...?a2?a1?2KM.

故数列?an?是B-数列.

x1＝1

33. (2009陕西卷理) 已知数列?xn}满足， 2x＝1

n＋1?x,n?N*

’1n.

???猜想数列{xn}的单调性，并证明你的结论；

|x12

n?1-xn|≤()n?1

（Ⅱ)证明：65。

x112513

证明（1）由2及xn+1?1?x得x2?3?x4?8，x4?

n21

由x2?x4?x6猜想：数列?x2n?是递减数列

下面用数学归纳法证明：

（1）当n=1时，已证命题成立（2）假设当n=k时命题成立，即x2k?x2k?2

1?3?x2k?1

易知x2k?0x2k?2?xx2k

2k?4?

，那么1?x?1?

2k?11?x2k?3(1?x2k?1)(1?x2k?3)

x2k?x2k?2

=(1?x?0

2k)(1?x2k?1)(1?x2k?2)(1?x2k?3)

即x2(k?1)?x2(k?1)?2

也就是说，当n=k+1时命题也成立，结合（1）和（2）知，命题成立

（2）当n=1时，n?1?xn?x2?x1?1

6，结论成立

?xn?1?1,?1?xn?1?2,xn?1

当n?20

时，易知1?x?1

n?12

选校网专业大全历年分数线上万张大学图片大学视频院校库 24

?(1?xn)(1?xn?1)?(1?15)(1?xn?1)?2?xn?1?1?xn?12

?xn?1?xn?xn?xn?111??1?xn1?xn?1(1?xn)(1?xn?1)

2222n-1xn?xn?1?（）xn?1?xn?2???（）x2?x1555

12n-1?）

65 ?

35.（2009天津卷理）已知等差数列{}的公差为d（d?0），等比数列{

?bn}的公比为q（q>1）sabab。设n=11+22…..+ anbn

若n?1Tabab)n1122,=-+…..+(-1 anbn,n?N a1=b1= 1，d=2，q=3，求 S3 的值；

2dq(1?q2n)

2?bST1?q12n2n若=1，证明（1-q）-（1+q）=，n?N；

(Ⅲ) 若正数n满足2?n?q，设k1,.k..,2,,..k.,n和1.12..2llc?ak1b1?ak2b2?...?aknbnln是，，，n的两个不同的排列， 1， c2?al1b1?al2b2?...?alnbnc1?c2 证明。

本小题主要考查等差数列的通项公式、等比数列的通项公式与前n项和公式等基础知识，考查运算能力，推理论证能力及综合分析和解决问题的能力的能力，满分14分。

n?1*a?2n?1,b?3,n?Nnn（Ⅰ）解：由题设，可得

所以，S3?a1b1?a2b2?a3b3?1?1?3?3?5?9?55

n?1b?q（Ⅱ）证明：由题设可得n则

S2n?a1?a2q?a3q2?.....?a2nq2n?1, ①

T2n?a1?a2q?a3q2?a4q3?.....?a2nq2n?1,

S2n?T2n?2(a2q?a4q3?...?a2nq2n?1)

式减去②式，得

式加上②式，得

2S?T?2(a?aq?....?a2n2n13?n2 2n?2

1 ② q ③ )

式两边同乘q，得

3q(S?T)?2(aq?aq?....??a2n2n13n2 2n?1

1 q)

25 选校网专业大全历年分数线上万张大学图片大学视频院校库

所以，

(1?q)S2n?(1?qT2)n?S(2n?T2n)?q(2Sn?2T n)

?2d(q?q3?K?q2n?1)

?2dq(1?q2n),n?N*

1?q2

(Ⅲ)证明：c1?c2?(ak1?al1)b1?(ak2?al2)b2?K?(akn?aln)bn

?(k1?l1)db1?(k2?ln?1

2)db1q?K?(kn?ln)db1q

因为d?0,b1?0,所以

c1?c2?(k1?l1)?(k1

2?l2)q?K?(kn?ln)qn?

db1

若kn?ln，取i=n

若kn?ln，取i满足ki?li且kj?lj,i?1?j?n

由（1）,(2)及题设知，1?i?n且

c1?c2?(k2

1?l1)?(k2?l2)q?K(ki?1?li?1)qi??(ki?1

i?li)q

db1

当ki?li时，得ki?li??1,由q?n，得ki?li?q?1,i?1,2,3.....i?1

即k1?l1?q?1，(k2?l2)q?q(q?1)…，(ki?2i?2

i?1?li?1)q?q(q?1)

又(ki?li)qi?1??qi?1,所以

c1?c2?(q?1)?(q?1)q?K(q?1)q?2?qi?1?(q1?qi?1

db?1)

11?q

因此c1?c2?0,即c1?c2

c1?c2

当ki?l??1

i同理可得db1，因此c1?c2

综上，c1?c2

37.（20xx年上海卷理）已知?an?是公差为d的等差数列，?bn?是公比为q的等比数列。若an?3n?1，是否存在m、k?N*，有am?am?1?ak?说明理由；

选校网专业大全历年分数线上万张大学图片大学视频院校库 26

an?1?bn*ba????a找出所有数列n和n，使对一切n?N,n,并说明理由；

若a1?5,d?4,b1?q?3,试确定所有的p，使数列?an?中存在某个连续p项的和是数列?bn?中的一项，请证明。

am?am?1?ak，得6m?5?3k?1，．．．．．．2分

3，?m、k?N?，?k?2m为整数， [解法一]（1）由k?2m?整理后，可得

??不存在m、k?N，使等式成立。．．．．．．5分

an?1a1?nd?bn?b1qn?1

aa?(n?1)d（2）若，即1，（*）

1?b1q（ⅰ）若d?0,则

当{n?1?bn。 an}为非零常数列，{bn}为恒等于1的常数列，满足要求。．．．．．．7分

lima1?nd?1n??a?(n?1)d1（ⅱ）若d?0，（*）式等号左边取极限得，（*）式等号右边的极限只有当q?1时，才能等于1。

此时等号左边是常数，?d?0，矛盾。综上所述，只有当{an}为非零常数列，{bn}为恒等于1的常数列，满足要求。．．．．．．10分

an?1?bn,且?bn?为等比数列an an?nd?c,若

【解法二】设

an?2an?1/?q,对n?N*都成立，即anan?2?qa2

n?1aan则n?1

?(dn?c)(dn?2d?c)?q(dn?d?c)2对n?N*都成立，?a2?qd2....7分

*a?c?0,?b?1,n?Nnn若d=0，则

dn?d?c?m?b?md?0,则q=1,dn?cn若（常数）即，则d=0，矛盾

an?c?0,bn?1,使对一切n?N*,

综上所述，有

na?4n?1,b?3,n?N* nn（3）an?1?bnan， 10分

设am?1?am?2????am?p?bk?3k,p、k?N*,m?N.

27 选校网专业大全历年分数线上万张大学图片大学视频院校库

4(m?1)?1?4(m?p)?1

2p?3k，

?4m?2p?3?3k

p,?p、k?N*,?p?35,s?N

. 13分

取k?3s?2,4m?32s?2?2?3s?3?(4?1)2s?2?2?(4?1)s?3?0, 15分由二项展开式可得正整数M1、M2，使得（4-1）2s+2=4M1+1,

2?(4?1)s?8M2?(?1)s2,

?4m?4(M1?2M2)??(?1)s?1?2,?存在整数m满足要求.

故当且仅当p=3s,s?N时，命题成立.

说明：第（3）题若学生从以下角度解题，可分别得部分分（即分步得分）若p为偶数，则am+1+am+2+??+am+p为偶数，但3k为奇数

故此等式不成立，所以，p一定为奇数。

当p=1时，则am+1=bk,即4m+5=3k，

而3k=(4-1)k

0k1

=Ck?4?Ck?4k?1?(?1)????Ck?1

k?4?(?1)k?1?Ck

k?(?1)k?4M?(?1)k,M?Z,

当ｋ为偶数时，存在ｍ，使４ｍ＋５＝3k成立 1分当p=3时，则am+1+am+2+am+3=bk,即3am+2-bk,

也即3（4m+9）=3k,所以4m+9=3k-1,4(m+1)+5=3k-1

由已证可知，当k-1为偶数即k为奇数时，存在m, 4m+9=3k成立 2分当p=5时，则am+1+am+2+??+am+5=bk,即5am+3=bk

也即5（4m+13）=3k,而3k不是5的倍数，所以，当p=5时，所要求的m不存在故不是所有奇数都成立. 2分

三、解答题

10.（2008全国I）设函数f(x)?x?xlnx．数列?an?满足0?a1?1，an?1?f(an)．（Ⅰ）证明：函数f(x)在区间(0，1)是增函数；（Ⅱ）证明：an?an?1?1；

k≥a1?b

（Ⅲ）设b?(a1，1)，整数a1lnb．证明：ak?1?b．

（Ⅰ）证明：f(x)?x?xlnx，f'?x???lnx,当x??0,1?时，f'?x???lnx?0 故函数f?x?在区间(0,1)上是增函数；

（Ⅱ）证明：（用数学归纳法）（i）当n=1时，0?a1?1，a1lna1?0，

a2?f(a1)?a1?a1lna1?a1

选校网专业大全历年分数线上万张大学图片大学视频院校库 28

，1)，1]由函数f(x)在区间(0是增函数，且函数f(x)在x?1处连续，则f(x)在区间(0是增函数，

a2?f(a1)?a1?a1lna1?1，即a1?a2?1成立；

（ⅱ）假设当x?k(k?N*)时，ak?ak?1?1成立，即0?a1≤ak?ak?1?1

1]是增函数，0?a1≤ak?ak?1?1得那么当n?k?1时，由f(x)在区间(0，

f(ak)?f(ak?1)?f(1).而an?1?f(an)，则ak?1?f(ak),ak?2?f(ak?1)，

ak?1?ak?2?1，也就是说当n?k?1时，an?an?1?1也成立；

根据（ⅰ）、（ⅱ）可得对任意的正整数n，an?an?1?1恒成立.

a?f(an)可（Ⅲ）证明：由f(x)?x?xlnx．n?1

?a1?b??ailnaia?b?a?b?alnak?1kkki?1

若存在某i≤k满足

若对任意i≤k都有

kkai≤b，则由⑵知：，则ak?1?b?ai?b≥0 ai?ba?b?a?b?alnak?1kkk kk

?a1?b??ailnai?a1?b??ailnb?a1?b?(?ai)lnb

i?1i?1i?1?a?b?kalnb11

?a?b?kalnb?a?b?(a?b)?0，即ak?1?b成立. 1111

11.（2008山东卷)将数列｛an｝中的所有项按每一行比上一行多一项的规则排成如下数表：

a2 a3

a4 a5 a6

a7 a8 a9 a10

2bn

2bS?SnnN记表中的第一列数a1，a2，a4，a7，?构成的数列为｛bn｝,b1=a1=1. Sn为数列｛bn｝的前n项和，且满足＝1=

（n≥2）.

S(Ⅰ)证明数列｛n｝成等差数列，并求数列｛bn｝的通项公式；

a81??4

91时，（Ⅱ）上表中，若从第三行起，每一行中的数按从左到右的顺序均构成等比数列，且公比为同一个正数.当

求上表中第k(k≥3)行所有项和的和.

选校网专业大全历年分数线上万张大学图片大学视频院校库 29

xA(a，b)a?a，Sn是数列{an}的前n项和，且满足y?en?N*nnn12.(2007湖南)已知（）是曲线上的点，1

22Sn?3n2an?Sn3，4，?1，an?0，n?2，?．

?bn?2???b（I）证明：数列?n?（n≤2）是常数数列；

（II）确定a的取值集合M，使a?M时，数列

（III）证明：当a?M时，弦{an}是单调递增数列； AnAn?1（n?N*）的斜率随n单调递增

222S?S?3nan． n≥2n?1解：（I）当时，由已知得n

2a?S?S?0S?S?3nnnn?1nn?1因为，所以． ?? ①

2S?S?3(n?1)n?1n于是． ??②

由②－①得

于是an?1?an?6n?3． ?? ③ an?2?an?1?6n?9． ?? ④

an?2?an?6， ?? ⑤ 由④－③得

?bn?2?bn?2ean?2an?2?an6?an?e?e??(n≥2)bbe所以n，即数列?n?是常数数列．

（II）由①有S2?S1?12，所以a2?12?2a．由③有a3?a2?15，a4?a3?21，所以a3?3?2a，a4?18?2a．

{a2k}和{a2k?1}分别是以a2，a3为首项，6为公差的等差数列，而 ⑤表明：数列

所以

数列a2k?a2?6(k?1)，a2k?1?a3?6(k?1)，a2k?2?a4?6(k?1)(k?N*)， {an}是单调递增数列?a1?a2且a2k?a2k?1?a2k?2对任意的k?N*成立． ?a1?a2且a2?6(k?1)?a3?6(k?1)?a4?6(k?1)

?a1?a2?a3?a4?a?12?2a?3?2a?18?2a?915?a?44．

?915?M??a?a??4?． ?4即所求a的取值集合是

bn?1?bnean?1?eankn??AAa?aan?1?an n?1n（III）解法一：弦nn?1的斜率为

选校网专业大全历年分数线上万张大学图片大学视频院校库 30

ex(x?x0)?(ex?ex0)ex?ex0f(x)?f(x)?2xx?x(x?x)00，则0任取，设函数

x0xx?(x)?ex(x?x0)?ex?ex?ex(x?x0)g(x)?e(x?x)?(e?e)g0记，则，

当

当x?x0时，g?(x)?0，g(x)在(x0，??)上为增函数， x?x0时，g?(x)?0，g(x)在(??，x0)上为减函数，

x?x0时，g(x)?g(x0)?0，从而f?`(x)?0，所以f(x)在(??，x0)和(x0，??)上都是增函数．

{an}单调递增，所以由（II）知，a?M时，数列

ean?1?eanean?2?eankn??x?aa?a?aa?aan?2?an． n，因为nn?1n?2，所以n?1n取0

ean?1?ean?2ean?ean?2kn?1??x?an?2，因为an?an?1?an?2，所以an?1?an?2an?an?2．取0

所以kn?kn?1，即弦AnAn?1(n?N*)的斜率随n单调递增．

ex?ean?1f(x)???)上都是增函数， x?an?1，同解法一得，f(x)在(??，an?1)和(an?1，解法二：设函数

ean?ean?1ex?ean?1ean?2?ean?1ex?ean?1an?1an?1kn??lim?ek??lim?en?1?n→a?n→ana?aa?a?1x?an?1x?an?1nn?1n?2n?1n?1所以，．

故kn?kn?1，即弦AnAn?1(n?N*)的斜率随n单调递增．

1222?4?1,记S?a?a???a,n12n2an5.（辽宁省沈阳二中2008—2009学年上学期高三期中考试） {an}满足a1?1,an?1数列

m的最小值

A．10 B．9

答案：A.

若S2n?1?Sn?m30对任意n?N*恒成立，则正整数（） C．8 D．7

选校网专业大全历年分数线上万张大学图片大学视频院校库 31

相关推荐

瓷砖知识大总结

第二篇：高中数列知识大总结(绝对全)

专栏推荐