运筹学实验报告0920xx234)

运筹学实验报告

开课系部及实验室： 11层多功能实验室实验时间：20##-5-17

1、实验目的：

1. 了解、使用MATLAB中的优化命令求解线性规划、非线性规划、二次规划等问题;

2. 了解用lindo软件求解线性规划。

2、实验仪器、设备及材料：

Lindo11.0软件，计算机,MATLAB2010rb软件，管理运筹学2.5

3、实验内容：

线性规划（linear programming）是运筹学中应用最广泛的模型之一。由于其理论和方法研究比较成熟，许多问题常借助线性规划模型来求解，而且线性规划为某些非线性规划问题的解法起到间接作用。

1.1 线性规划的模型结构

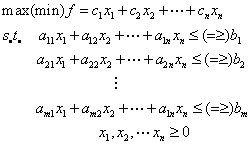
线性规划的标准形式为：

1.2 单纯形算法

根据单纯形法的原理编写MATLAB程序：simpleTab

MATLAB优化库函数都是以最小化为标准，所以simpleTab（mat,numFreeVar）程序也以最优化为标准。

simpleTab的使用方法为：

先将一般的线性规划变为线性规划的标准形式，再构建初始单纯形表格，输入程序。

：

1.3 linprog函数

linprog函数在MATLAB优化工具箱Optimization-Toolbox中。

linprog针对的线性函数模型为

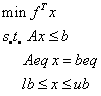
具体用法可以help linprog

实例演示1

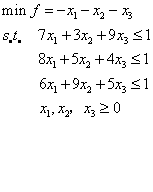
使用[x,fval,exitflag,output,lambda] = linprog(f,A,b,Aeq,beq,lb,ub)

在命令窗口输入：

f = [-1,-1,-1] %目标函数系数

A= [7, 3, 9; 8, 5, 4; 6, 9, 5]; %不等式约束的系数矩阵

b= [1, 1, 1] %不等式约束的b

Aeq=[] %等式约束的系数矩阵（该问题无等式约束Aeq为空）

beq=[] %等式约束的beq（该问题无等式约束beq为空）

lb=[0, 0, 0] %变量的下届

ub=[] %变量得上界（无上界约束，ub为空）

[x,fval,exitflag,output,lambda] = linprog(f,A,b,Aeq,beq,lb,ub)

运行结果：

f =

-1 -1 -1

b =

1 1 1

Aeq =

[]

beq =

[]

lb =

0 0 0

ub =

[]

Optimization terminated.

x =

0.0870

0.0356

0.0316

fval =

-0.1542

exitflag =

output =

iterations: 7

algorithm: [1x27 char]

cgiterations: 0

message: [1x24 char]

constrviolation: 0

firstorderopt: 3.2143e-014

lambda =

ineqlin: [3x1 double]

eqlin: [0x1 double]

upper: [3x1 double]

lower: [3x1 double]

1.4 用lingo11.0软件求解

例1某家具公司制造书桌、餐桌和椅子，所用的资源有三种：木料、木工和漆工。生产数据如下表所示：

若要求桌子的生产量不超过5件，如何安排三种产品的生产可使利润最大？

用DESKS、TABLES和CHAIRS分别表示三种产品的生产量，建立LP模型。

max=60*desks+30*tables+20*chairs;

8*desks+6*tables+chairs<=48;

4*desks+2*tables+1.5*chairs<=20;

2*desks+1.5*tables+.5*chairs<=8;

tables<=5;

求解这个模型，并激活灵敏性分析。这时，查看报告窗口（Reports Window）,可以看到如下结果。

Global optimal solution found at iteration: 3

Objective value: 280.0000

Variable Value Reduced Cost

DESKS 2.000000 0.000000

TABLES 0.000000 5.000000

CHAIRS 8.000000 0.000000

Row Slack or Surplus Dual Price

1 280.0000 1.000000

2 24.00000 0.000000

3 0.000000 10.00000

4 0.000000 10.00000

5 5.000000 0.000000

“Global optimal solution found at iteration: 3”表示3次迭代后得到全局最优解。 “Objective value:280.0000”表示最优目标值为280。 “Value”给出最优解中各变量的值：造2个书桌（desks）, 0个餐桌（tables）, 8个椅子（chairs）。所以desks、chairs是基变量（非0），tables是非基变量（0）。

“Slack or Surplus”给出松驰变量的值：

第1行松驰变量 =280（模型第一行表示目标函数，所以第二行对应第一个约束）

第2行松驰变量 =24

第3行松驰变量 =0

第4行松驰变量 =0

第5行松驰变量 =5

“Reduced Cost”列出最优单纯形表中判别数所在行的变量的系数，表示当变量有微小变动时, 目标函数的变化率。其中基变量的reduced cost值应为0，对于非基变量 Xj, 相应的 reduced cost值表示当某个变量Xj 增加一个单位时目标函数减少的量( max型问题)。本例中：变量tables对应的reduced cost值为5，表示当非基变量tables的值从0变为 1时（此时假定其他非基变量保持不变,但为了满足约束条件，基变量显然会发生变化），最优的目标函数值 = 280 - 5 = 275。

“DUAL PRICE”（对偶价格）表示当对应约束有微小变动时, 目标函数的变化率。输出结果中对应于每一个约束有一个对偶价格。若其数值为p，表示对应约束中不等式右端项若增加1 个单位，目标函数将增加p个单位（max型问题）。显然，如果在最优解处约束正好取等号（也就是“紧约束”，也称为有效约束或起作用约束），对偶价格值才可能不是0。本例中：第3、4行是紧约束，对应的对偶价格值为10，表示当紧约束

3) 4 DESKS + 2 TABLES + 1.5 CHAIRS <= 20

变为 3) 4 DESKS + 2 TABLES + 1.5 CHAIRS <= 21

时，目标函数值 = 280 +10 = 290。对第4行也类似。

对于非紧约束（如本例中第2、5行是非紧约束），DUAL PRICE 的值为0, 表示对应约束中不等式右端项的微小扰动不影响目标函数。有时, 通过分析DUAL PRICE, 也可对产生不可行问题的原因有所了解。

灵敏度分析的结果是

Ranges in which the basis is unchanged:

Objective Coefficient Ranges

Current Allowable Allowable

Variable Coefficient Increase Decrease

DESKS 60.00000 0.0 0.0

TABLES 30.00000 0.0 0.0

CHAIRS 20.00000 0.0 0.0

Righthand Side Ranges

Row Current Allowable Allowable

RHS Increase Decrease

2 48.00000 0.0 0.0

3 20.00000 0.0 0.0

4 8.000000 0.0 0.0

5 5.000000 0.0 0.0

目标函数中DESKS变量原来的费用系数为60，允许增加（Allowable Increase）=4、允许减少（Allowable Decrease）=2，说明当它在[60-4，60+20] = [56，80]范围变化时，最优基保持不变。对TABLES、CHAIRS变量，可以类似解释。由于此时约束没有变化（只是目标函数中某个费用系数发生变化），所以最优基保持不变的意思也就是最优解不变（当然，由于目标函数中费用系数发生了变化，所以最优值会变化）。

第2行约束中右端项（Right Hand Side，简写为RHS）原来为48，当它在[48-24，48+∞] = [24，∞]范围变化时，最优基保持不变。第3、4、5行可以类似解释。不过由于此时约束发生变化，最优基即使不变，最优解、最优值也会发生变化。

灵敏性分析结果表示的是最优基保持不变的系数范围。由此，也可以进一步确定当目标函数的费用系数和约束右端项发生小的变化时，最优基和最优解、最优值如何变化。下面我们通过求解一个实际问题来进行说明。

例2一奶制品加工厂用牛奶生产A₁,A₂两种奶制品，1桶牛奶可以在甲车间用12小时加工成3公斤A₁，或者在乙车间用8小时加工成4公斤A₂。根据市场需求，生产的A₁,A₂全部能售出，且每公斤A₁获利24元，每公斤A₂获利16元。现在加工厂每天能得到50桶牛奶的供应，每天正式工人总的劳动时间480小时，并且甲车间每天至多能加工100公斤A₁，乙车间的加工能力没有限制。试为该厂制订一个生产计划，使每天获利最大，并进一步讨论以下3个附加问题：

1）若用35元可以买到1桶牛奶，应否作这项投资？若投资，每天最多购买多少桶牛奶？

2）若可以聘用临时工人以增加劳动时间，付给临时工人的工资最多是每小时几元？

3）由于市场需求变化，每公斤A₁的获利增加到30元，应否改变生产计划？

模型代码如下：

max=72*x1+64*x2;

x1+x2<=50;

12*x1+8*x2<=480;

3*x1<=100;

求解这个模型并做灵敏性分析，结果如下。

Global optimal solution found at iteration: 0

Objective value: 3360.000

Variable Value Reduced Cost

X1 20.00000 0.000000

X2 30.00000 0.000000

Row Slack or Surplus Dual Price

1 3360.000 1.000000

2 0.000000 48.00000

3 0.000000 2.000000

4 40.00000 0.000000

Ranges in which the basis is unchanged:

Objective Coefficient Ranges

Current Allowable Allowable

Variable Coefficient Increase Decrease

X1 72.00000 24.00000 8.000000

X2 64.00000 8.000000 16.00000

Righthand Side Ranges

Row Current Allowable Allowable

RHS Increase Decrease

2 50.00000 10.00000 6.666667

3 480.0000 53.33333 80.00000

4 100.0000 INFINITY 40.00000

结果告诉我们：这个线性规划的最优解为x₁=20，x₂=30，最优值为z=3360，即用20桶牛奶生产A₁, 30桶牛奶生产A₂，可获最大利润3360元。输出中除了告诉我们问题的最优解和最优值以外，还有许多对分析结果有用的信息，下面结合题目中提出的3个附加问题给予说明。 3个约束条件的右端不妨看作3种“资源”：原料、劳动时间、车间甲的加工能力。输出中Slack or Surplus给出这3种资源在最优解下是否有剩余：原料、劳动时间的剩余均为零，车间甲尚余40（公斤）加工能力。

目标函数可以看作“效益”，成为紧约束的“资源”一旦增加，“效益”必然跟着增长。输出中DUAL PRICES 给出这3种资源在最优解下“资源”增加1个单位时“效益”的增量：原料增加1个单位（1桶牛奶）时利润增长48（元），劳动时间增加1个单位（1小时）时利润增长2（元），而增加非紧约束车间甲的能力显然不会使利润增长。这里，“效益”的增量可以看作“资源”的潜在价值，经济学上称为影子价格，即1桶牛奶的影子价格为48元，1小时劳动的影子价格为2元，车间甲的影子价格为零。读者可以用直接求解的办法验证上面的结论，即将输入文件中原料约束milk）右端的50改为51，看看得到的最优值（利润）是否恰好增长48（元）。用影子价格的概念很容易回答附加问题1）：用35元可以买到1桶牛奶，低于1桶牛奶的影子价格48，当然应该作这项投资。回答附加问题2）：聘用临时工人以增加劳动时间，付给的工资低于劳动时间的影子价格才可以增加利润，所以工资最多是每小时2元。

目标函数的系数发生变化时（假定约束条件不变），最优解和最优值会改变吗？这个问题不能简单地回答。上面输出给出了最优基不变条件下目标函数系数的允许变化范围：x₁的系数为（72-8，72+24）=（64，96）；x₂的系数为（64-16，64+8）=（48，72）。注意：x₁系数的允许范围需要x₂系数64不变，反之亦然。由于目标函数的费用系数变化并不影响约束条件，因此此时最优基不变可以保证最优解也不变，但最优值变化。用这个结果很容易回答附加问题3）：若每公斤A₁的获利增加到30元，则x₁系数变为30×3=90，在允许范围内，所以不应改变生产计划，但最优值变为90×20+64×30=3720。

4、实验总结：

在此次实验中，对运筹学软件有了一定的的认识，熟悉了运筹学软件的安装和使用方法，也掌握了线性规划问题在运筹学软件中的求解步骤。与图解法求解相比运用软件使得求解变得迅捷无比。

相关推荐

运筹学实验报告0920xx234)

专栏推荐