Matlab总结

Matlab个人总结

matlab常用到的永久变量。
ans：计算结果的默认变量名。
i j：基本虚数单位。
eps：系统的浮点(F10a9Bg个oht)：
inf:无限大，例1/0
nan NaN：非数值(N航a nmnb谢)
pi：圆周率n(n＝3．1415926．．)。
realmax：系统所能表示的最大数值。
realmin:系统所能表示的最小数值，
nargin:函数的输入参数个数：
nargout：函数的输出多数个数

①matlab的所有运算都定义在复数城上。对于方根问题运算只返回处于第一象限的解。
⑦matlab分别用左斜／和右\来表示“左除和“右除”运算。对于标量运算而言，这两者的作用没有区别：但对于矩阵运算来说，二者将产生不同的结果。

多项式的表示方法和运算
p(x)=x^3-3x-5可以表示为p=[1 0–3 5],求x＝5时的值用plotval(p,5)
也可以求向量：a=[3 4 5],plotval(p,a)
函数roots求多项式的根roots(p)
p=[1 0 -3 5];
r=roots(p)
由根重组多项式poly(根)
q=poly(r)
real(q)有时会产生虚根，这时用real抽取实根即可
conv(a,b)函数多项式乘法（执行两个数组的卷积）
a=[1 2 3 4];
b=[1 4 9 16];
c=conv(a,b)
多项式的加减法，低阶的多项式必须用首零填补，使其与高阶多项式有同样的阶次
多项式除法[q , r]=deconv(c , b)表示b/c q为商多项式，r为余数
多项式的导数polyder(f)
f=[ 2 4 5 6 2 1];
s=polyder(f)

多项式的曲线拟合
x=[1 2 3 4 5];
y=[5.6 40 150 250 498.9];
p=polyfit(x,y,n)数据的n次多项式拟合poly：矩阵的特征多项式、根集对应的多项式
x2=1:0.1:5; n取1时，即为最小二乘法
y2=polyval(p,x2);计算多项式的值（polyvalm计算矩阵多项式）
plot(x,y,'*',x2,y2);grid on
最小二乘法
x=[1 2 3 4 5];
y=[5.6 40 150 250 498.9];
plot(x,y,’*’),lsline

多项式插值（p158）
YI=interp1(x,y,XI,’method’)一维插值
(XI为插值点的自变量坐标向量,可以为数组或单个数。
method为选择插值算法的方法，包括：
linear(线性插值)
cubic(立方插值)
spline(三次样条插值)
nearst(最近临插值)

例如：人口预测
year=1900:10:1900;
number=[78 91 105….每十年的人口数];
x=1900:1:2000;
y=interp1(year,number,x,’spline’);
plot(year,numeber,’*’,x,y);grid on

一维博里叶变换插值使用函数interpft实现，计算含有周期函数值的矢量的傅里叶变换
然后使用更多的点进行傅里叶变换的逆变换，函数的使用格式如下：y=interpft(x,n)其中x是含有周期函数值的矢量，并为等距的点，n为返同等间距点的个数。

求解一元函数的最小值
y=fminbnd('humps',0.3,1) humps为一内置函数
求解多元函数的最小值
函数fminserch用于求多元函数的最小值。它可以指定一个开始的矢量，并非指定一个区间。此函数返回一个矢量为此多元函数局部最小函数值对应的自变量

纹理成图功能
由warp函数的纹理成图功能实现平面图像在空间三维曲面上的显示。
将文件名为flowers.tif的图像分别投影到圆柱形和球星表面上
i=imread('flowers.tif');
[x,y,z]=cylinder;
subplot(1,2,1),warp(x,y,z,i);
[x,y,z]=sphere(50);
subplot(1,2,2),warp(x,y,z,i);
warp(x,y,z,i);

求函数的零点
求函数humps在[1，2]区间上的零点fzero(‘humps’,[1,2]);
也可以给一个初始值fzero(‘humps’,0.9);
对于多项式可直接由roots求其根roots(‘4*x^3+……’);
也可以用solve
c=sym('c','real');
x=sym('x','real');
s=solve(x^3-x+c)

函数定积分
q=quadl(‘humps’,0,1)求humps函数在0 1区间上的定积分，也可以用quad语句

二重积分首先计算内积分，然后借助内积分的中间结果再求出二重积分的值，类似于积分中的分步积分法。
Result=dblquad(‘integrnd’,xin,xmax.,ymin,ymax) integrnd为被积函数的名称字符串

符号积分运算int(f)
最精确的是符号积分法
计算s=∫12[∫01xydx]dy
syms x y中间为空格，不能为逗号
s=int(int(‘x^y’,’x’,0,1),’y’,1,2)引号可省略
vpa(s)显示s的值
内积分限为函数的二重积分
I=∫14[∫√y2(x2+y2)dx]dy
符号法I=vpa(int(int(‘x^2+y^2’,’x’,sqrt(y),2),’y’,1,4)

微分运算（diff）
微分是描述一个函数在一点处的斜率，是函数的微观性质、因此积分对函数的形状在小范围内的改变不敏感，而微分很敏感。—个函数的小的变化，容易产生相邻点的斜率的大的改变。由干微分这个固有的困难．所以尽可能避免数值微分．特别是对实验获得的数据进行微分。在这种情况，最好用最小二乘曲线拟合这种数据，然后对所得到的多项式进行微分；或用另一种方法对点数据进行三次样条拟合，然后寻找样条微分，但是，有时微分运算是不能避免的，在MATLAB中．用函数diff汁算一个矢量或者矩阵的微分(也可以理解为差分)。
a=[1 2 3 3 3 7 8 9];
b=diff(a)一次微分
bb=diff(a,2)二次微分
实际上diff(a)=[a(2)-a(1),a(3)-a(2),……,a(n)-a(n-1)]
对于求矩阵的微分，即为求各列矢量的微分，从矢量的微分值可以判断矢量的单调性、是否等间距以及是否有重复的元素。
符号微分运算(diff)
syms x t a
f =cos(a*x)
df =diff(f)由findsym的规则，隐式的指定对x进行微分
dfa=diff(f,'a')指定对变量a进行微分
dfa=diff(f,'a',3)三次微分
diff函数不仅作用在标量上，还可以在矩阵上，运算规则就是按矩阵的元素分别进行微分
syms a x
A=[cos(a*x),sin(a*x),-sin(a*x),cos(a*x)];
dA=diff(A)
微分方程dsolve
在matlab中，符号表达式中包含字母D用来表示微分运算，D2,D3分别对应第二，第三阶导数，D2y表示d2y/dt2把t缺省了
y=dsolve(‘Dy=f(y)’)单个方程，单个输出
[u,v]=dsolve(‘Du=f(u,v)’,’Dv=g(u,v)’) 2个方程，2个输出
s=dsolve(‘Dx=f(x,y,z)’,’Dy=g(x,y,z)’,’Dz=k(x,y,z)’)
s.x s.y s.z 3个方程，架构数组

dsolve('Dx=-a*x')结果：C1*exp(-a*t)没给定初值，所以结果中含参变量
x=dsolve('Dx=-a*x','x(0)=1','s')结果exp(-a*s)给定了初值，独立变量设为s
计算多元函数的梯度
fx=gradient(f) f是一个矢量返回f的一维数值梯度，fx对应于x方向的微分。

[x,y]=meshgrid(-2:.2:2,-2:.2:2);
z=x.*exp(-x.^2-y.^2);
[px,py]=gradient(z,.2,.2);
contour(z),hold on画等值线
quiver(px,py)

matlab字符串运算
利用sym命令创建表达式
f=sym(‘cos(x)+sin(x)’)或syms x , f=cos(x)+sin(x)
diff(f)求其导数
（也可直接用命令f=diff(‘cos(x)+cos(y)’)

当字符表达式中含有多于一个的变量时，只有—个变量是独立变量。如果不告诉matlab哪一个变量是独立变量，则可以通过findsym命令询问
利用findsym命令查询独立变量
f=sym('sin(a*x)+b')
findsym(f,1)给出独立变量（一个变量，如果为2则给出2个变量）
findsym(f)给出所有变量

符号表达式的化简和替换
collect函数</

在MATLAB下，如果notebook不能正常使用，即在输入了notebook命令后，屏幕显示：

>> notebook

??? Error using ==> notebook (getAndVerifyNotebookProfl)

Notebook has not been configured properly. Please run notebook -setup

Error in ==> C:\MATLAB6P5\toolbox\matlab\general\notebook.m

On line 42 ==> [wordPath, wordTempPath] = getAndVerifyNotebookProfl;

这时可以使用以下命令对notebook进行设置：

>> notebook -setup

Welcome to the utility for setting up the MATLAB Notebook

for interfacing MATLAB to Microsoft Word

Choose your version of Microsoft Word:

[1] Microsoft Word 97

[2] Microsoft Word 2000

[3] Microsoft Word 20## (XP)

[4] Exit, making no changes

Microsoft Word Version: 3

Notebook setup is complete.

下面再输入MATLAB即可正常启动：

>>notebook

5.2实验内容

1）至少用3种方法解方程组Ax=b，如矩阵除法、求逆矩阵、通过初等变换将矩阵化为上（下）三角阵等，其中

，

方法1：a=[-3,5,0,8;1,-8,2,-1;0,-5,9,3;-7,0,-4,5];b=[0;2;-1;6];x=a\b

x =

-0.6386

-0.4210

-0.3529

0.0237

解：方法2：A=inv(a);x=A*b

x =

-0.6386

-0.4210

-0.3529

0.0237

方法3：[l,u]=lu(a);y=l\b,x=u\y

y =

6.0000

2.8571

-2.7857

0.1101

x =

-0.6386

-0.4210

-0.3529

0.0237

2)设有分块矩阵，其中E，R，O，S分别为单位阵、随机阵、零阵和对角阵，试通过数值计算验证。

解：E=eye(3);R=rand(3,2);O=zeros(2,3);S=[2,0;0,3];A=[E,R;O,S],A*A,[E,R+R*S;O,S*S]

A =

1.0000 0 0 0.9218 0.4057

0 1.0000 0 0.7382 0.9355

0 0 1.0000 0.1763 0.9169

0 0 0 2.0000 0

0 0 0 0 3.0000

ans =

1.0000 0 0 2.7654 1.6228

0 1.0000 0 2.2146 3.7419

0 0 1.0000 0.5288 3.6676

0 0 0 4.0000 0

0 0 0 0 9.0000

ans =

1.0000 0 0 2.7654 1.6228

0 1.0000 0 2.2146 3.7419

0 0 1.0000 0.5288 3.6676

0 0 0 4.0000 0

0 0 0 0 9.0000

3）用命令magic(n)生成幻方矩阵，通过计算研究它的性质，如行和、列和、两条对角线和。

a=magic(3),s1=sum(a),s2=sum(a'),s3=sum(diag(a)),s4=sum(diag(fliplr(a)))

a =

8 1 6

3 5 7

4 9 2

s1 =

15 15 15

s2 =

15 15 15

s3 =

s4 =

4）设，，，，在上适当离散化，计算，，，。

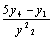x=-2:2;y1=1./(1+x.^2);y2=exp(-x.^2/2);y3=sin(2*x);y4=sqrt(4-x.^2);

a=y1+y2,b=y1.*y2,c=y3./y1,d=(5*y4-y1)./y2.^2

a =

0.3353 1.1065 2.0000 1.1065 0.3353

b =

0.0271 0.3033 1.0000 0.3033 0.0271

c =

3.7840 -1.8186 0 1.8186 -3.7840

d =

-10.9196 22.1819 9.0000 22.1819 -10.9196

5）某公司有8种产品，其单件的成本、售价及一段时间的销量如下：

计算这段时间的收入和利润：问哪种产品利润最大，问哪种产品利润最小；将各种产品的收入作一排序。

cb=[8.25 10.30 6.68 12.03 16.85 17.51 9.30 10.65];

sj=[15.00 16.25 9.90 18.25 20.80 24.15 15.50 18.25];

xl=[1205 580 395 2104 1538 810 694 1032];

lr=sj-cb,sr=(sj-cb).*xl

for i=1:8

if lr(i)==max(lr)

i,lr(i)

end

if lr(i)==min(lr)

i,lr(i)

end

'sort:',e=sort(lr.*xl)

lr =

Columns 1 through 7

6.7500 5.9500 3.2200 6.2200 3.9500 6.6400 6.2000

Column 8

7.6000

sr =

1.0e+004 *

Columns 1 through 7

0.8134 0.3451 0.1272 1.3087 0.6075 0.5378 0.4303

Column 8

0.7843

i =

ans =

3.2200

i =

ans =

7.6000

ans =

sort:

e =

1.0e+004 *

Columns 1 through 7

0.1272 0.3451 0.4303 0.5378 0.6075 0.7843 0.8134

Column 8

1.3087

6）自己选择一非负单调减序列，用从1到n和从n到1两种顺序计算，观察哪个更准确些，分析原因。如

s=0;

for k=1:100000

s=s+1/k;

end

's(1,2,3,…,100000)=',s

s1=0;

for k=100000:-1:1

s1=s1+1/k;

end

's1(100000,99999,99998,…,1)=',s1

ans =

s(1,2,3,…,100000)=

s =

12.09014612986334

ans =

s1(100000,99999,99998,…,1)=

s1 =

12.09014612986341

for k=1:100000

s=s-1/k;s1=s1-1/k;

end

s,s1

s =

-7.305902946150560e-014

s1 =

-2.283990460953331e-016

8）通过MATLAB的帮助系统掌握roots,poly,polyval的用法，并且用这些命令解以下问题：
1.已知一多项式的零点为{2,-3,1+2i,1-2i,0,-6}求这个多项式的系数（从高到低排列），并且计算多项式在点x=0.8,-1.2的值。

r=[2;-3;1+2i;1-2i;0;-6];

p=poly(r)

r1=roots(p)

p =

1 5 -9 -1 72 -180 0

r1 =

-6.00000000000001

-3.00000000000000

1.00000000000000 + 2.00000000000000i

1.00000000000000 - 2.00000000000000i

2.00000000000000

polyval(p,0.8)

polyval(p,1.2)

ans =

-1.002178560000000e+002

ans =

-1.172828160000000e+002

9）用几种方法作的图形，如一个图上画几条曲线。（注：若坐标不显示或者说图形显示不正常，可通过放大/缩小图形来显示）

x=-2:0.05:2;y=[x.^2;x.^3;x.^4;x.^5];z=0*x;

plot(x,y,x,z);grid on;legend('x^2','x^3','x^4','x^5')

10）用作图法求和的根的近似值。

x=1:0.01:4;y=x.^2-8.*log(x);z=0*x;plot(x,y,x,z,'k');axis([1 4 0 4])

故第一个方程根的近似值分别为1.2和3。

x=0:0.01:4;y=4*sin(x)-x-2;plot(x,y);axis([0 4 -2 2])

x=0:0.01:4;y=4*sin(x)-x-2;plot(x,y);axis([0 4 0 2])

两个图结合可以看到，方程的两个根的近似值分别为：0.75和1.8。

13）建立M-文件作以下计算：
1.自然数的阶乘；

为此，我们建立函数M-文件如下：

function f=factor(n)

p=1;

for i=1:n

p=p*i;

end

f=p;

将上述内容以文件名factor.m存盘后，可使用以下命令计算：

t=factor(5)

t =

120

3.已知任意两个多项式（不一定同阶）的系数，求两个多项式的和。

为此，我们建立函数M-文件如下：

a=length(p1);b=length(p2);

if a<b

p1=[zeros(1,b-a),p1];

elseif a>b

p2=[zeros(1,a-b),p2];

end

将上述内容以文件名f13-3.m存盘后，可使用以下命令计算：

p1=[1 0 3 5]

p2=[2 1 0]

f13_3

p=p1+p2

p1 =

1 0 3 5

p2 =

2 1 0

p2 =

0 2 1 0

p =

1 2 4 5

用MATLAB作插值计算：设n个节点以数组x0,y0输入，m个插值点以数组x输入，输出数组y为m个插值。比如一个名为lagr1.m的M文件内容为：

function y=lagr1(x0,y0,x)

n=length(x0);m=length(x);

for i=1:m

z=x(i);

s=0.0;

for k=1:n

p=1.0;

for j=1:n

if j~=k

p=p*(z-x0(j))/(x0(k)-x0(j));

end

s=s+p*y0(k);

end

y(i)=s;

end

作Lagrange插值时只需在输入x0,y0,x后运行：y=lagr1(x0,y0,x)即可；

分段线性插值有现成的程序：y=interp1(x0,y0,x)

三次样条插值也有现成的程序：y=interp1(x0,y0,x,'spline');此种方法属于自然边界条件。其他边界条件下的三次样条插值程序见MATLAB的样条工具包（Spline Toolbook）。

例：对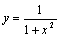，，用个节点（等分）作上述三种插值，用m(=21)个插值点（等分）作图，比较结果。其语句如下：

n=11;m=21;

x=-5:10/(m-1):5;

y=1./(1+x.^2);

z=0*x;

x0=-5:10/(n-1):5;

y0=1./(1+x0.^2);

y1=lagr1(x0,y0,x);

y2=interp1(x0,y0,x);

y3=interp1(x0,y0,x,'spline');

[x' y' y1' y2' y3']

plot(x,z,'r',x,y,'k:',x,y1,'y',x,y2,'b',x,y3,'o')

ans =

-5.0000 0.0385 0.0385 0.0385 0.0385

-4.5000 0.0471 1.5787 0.0486 0.0484

-4.0000 0.0588 0.0588 0.0588 0.0588

-3.5000 0.0755 -0.2262 0.0794 0.0745

-3.0000 0.1000 0.1000 0.1000 0.1000

-2.5000 0.1379 0.2538 0.1500 0.1401

-2.0000 0.2000 0.2000 0.2000 0.2000

-1.5000 0.3077 0.2353 0.3500 0.2973

-1.0000 0.5000 0.5000 0.5000 0.5000

-0.5000 0.8000 0.8434 0.7500 0.8205

0 1.0000 1.0000 1.0000 1.0000

0.5000 0.8000 0.8434 0.7500 0.8205

1.0000 0.5000 0.5000 0.5000 0.5000

1.5000 0.3077 0.2353 0.3500 0.2973

2.0000 0.2000 0.2000 0.2000 0.2000

2.5000 0.1379 0.2538 0.1500 0.1401

3.0000 0.1000 0.1000 0.1000 0.1000

3.5000 0.0755 -0.2262 0.0794 0.0745

4.0000 0.0588 0.0588 0.0588 0.0588

4.5000 0.0471 1.5787 0.0486 0.0484

5.0000 0.0385 0.0385 0.0385 0.0385

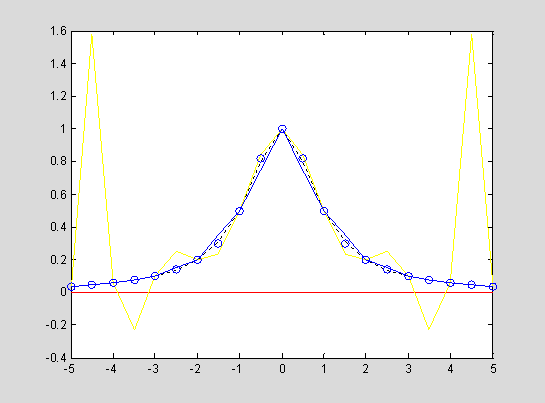
插值与拟合实验内容：

1．选择一些函数，在n个节点上，用拉格朗日、分段线性、三次样条三种插值方法，计算m个插值点的函数值，通过数值和图形输出。

a.y=sinx,

n=10;m=100;

x=linspace(0,2*pi,100);

y=sin(x);

z=x*0;

x0=linspace(0,2*pi,6);

y0=sin(x0);

y1=lagr1(x0,y0,x);

y2=interp1(x0,y0,x);

y3=interp1(x0,y0,x,'spline');

plot(x,z,x,y,'k',x,y1,x,y2,x,y3,'y')

n=10;m=100;b=0:0.1:1;a=b*0;

x=linspace(-1,1,100);

y=sqrt(1-x.*x);

z=x*0;

x0=linspace(-1,1,6);

y0=sqrt(1-x0.*x0);

y1=lagr1(x0,y0,x);

y2=interp1(x0,y0,x);

y3=interp1(x0,y0,x,'spline');

plot(x,z,x,y,'k',x,y1,x,y2,x,y3,'b',a,b,'k');

2．用在x=0,1,4,9,16产生5个节点，用不同的节点构造插值公式来计算x=5处的插值，与精确值比较并进行分析。

x0=[0 1 4 9 16];y0=sqrt(x0);x=5;y=sqrt(5)

y1=lagr1(x0,y0,x)

x0(1)=[];y0=sqrt(x0);y2=lagr1(x0,y0,x)

x0(4)=[];y0=sqrt(x0);y3=lagr1(x0,y0,x)

x0(1)=[];y0=sqrt(x0);y4=lagr1(x0,y0,x)

y =

2.2361

y1 =

2.0794

y2 =

2.2540

y3 =

2.2667

y4 =

2.2000

3．用给定的多项式，如，产生一组数据,再在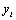上添加随机干扰，然后用和添加了随机干扰的作3次多项式拟合，与原系数比较，如果作2次或4次多项式拟合，结果如何？

x=2:0.1:6;p=[1 -6 5 -3];y=polyval(p,x);

x0=2:0.5:6;y0=polyval(p,x0);

r=rand(1,length(x0));y0=y0+r;

y3=polyfit(x0,y0,3);yy3=polyval(y3,x);

y2=polyfit(x0,y0,2);yy2=polyval(y2,x);

y4=polyfit(x0,y0,4);yy4=polyval(y4,x);

subplot(1,3,1),plot(x,y,'r',x,yy3,'b');title('three fit');

subplot(1,3,2),plot(x,y,'r',x,yy2,'b');title('two fit');

subplot(1,3,3),plot(x,y,'r',x,yy4,'b');title('4 fit');

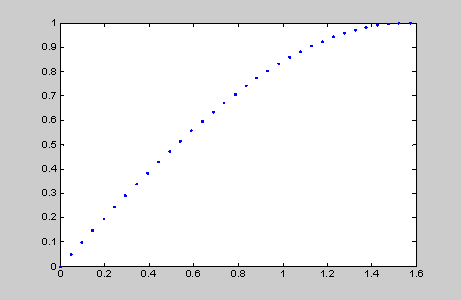
数值积分：

例用MATLAB计算

h=pi/20;

x=0:h:pi/2;

y=sin(x);

z1=sum(y(1:10))*h;

z2=sum(y(2:11))*h;

z=cumsum(y);

z11=z(10)*h;

z12=(z(11)-z(1))*h;

z3=trapz(y)*h;

format long

z4=quad('sin',0,pi/2,[0.0001,0.00001],1),%给出数值计算中间

z5=quad8('sin',0,pi/2,[0.0001,0.00001],1),%给出积分点的图形

z1,z11,z2,z12,z3

9 0.0000000000 4.26596866e-001 0.0896208493

11 0.4265968664 7.17602594e-001 0.4966040522

13 1.1441994604 4.26596866e-001 0.4137750613

z4 =

0.99999996278352

z5 =

1.00000000000000

z1 =

0.91940317001461

z11 =

0.91940317001461

z2 =

1.07648280269410

z12 =

1.07648280269410

z3 =

0.99794298635436

方程求根

牛顿法程序newton1.m的内容如下：

function y=newton1(x0,n,tol)

x(1)=x0;

b=1;

i=1;

while(abs(b)>tol*abs(x(i)))

x(i+1)=x(i)-fun1(x(i))/dfun1(x(i));

b=x(i+1)-x(i);

i=i+1;

if(i>n)error('n is full');

end

y=x(i);

例：1）用牛顿法求的两个根，准确到。

解：首先由作图知，该方程的两个根的大致范围为0或1.4：

fplot('fun1',[-1,2,0,0.6]);

其中fun1.m文件的内容为：

function y=fun1(x)

y=sin(x)-x*x/2;

其中dfun1.m文件的内容为：

function y=dfun1(x)

y=cos(x)-x;

我们用以下MATLAB命令计算方程在x=0附近根的近似值：

y=newton1(0.1,10,0.000001)

y =

我们用以下MATLAB命令计算方程在x=0附近根的近似值：

y=newton1(1.4,10,0.000001)

y =

1.4044

2）当为多项式时，可用r=roots(c)（其中c为多项式的系数向量，且按降幂排列；r为的全部根。如求的全部根，可使用以下MATLAB命令：

c=[1 -4 0 5];

r=roots(c)

r =

3.6180

1.3820

-1.0000

若已知的全部根r,也可以利用c=poly(r);求出原多项式，如：

c=poly(r)

c =

1.0000 -4.0000 0.0000 5.0000

若已知多项式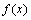，还可以利用函数df=polyder(c)求导函数：

df=polyder(c)

df =

3.0000 -8.0000 0.0000

MATLAB的符号运算：

1． 符号运算与符号表达式

可以用sym来定义一个符号或符号表达式，如：

sym('x')

ans =

r=sym('(1+sqrt(x))/2')

r =

(1+sqrt(x))/2

而且用sym可定义多个符号（符号之间用空格隔开，不能用逗号），如：

syms a b c k t y

f=a*(2*x-t)^3+b*sin(4*y)

f =

a*(2*x-t)^3+b*sin(4*y)

上面定义的各个符号和表达式可以进行运算，如：

g=f+a*(2*r-1)^3

g =

a*(2*x-t)^3+b*sin(4*y)+a*x^(3/2)

可以用findsym来确认符号表达式中的符号，如：

findsym(g)

ans =

a, b, t, x, y

2.微积分运算：

设a,b,t,x,y是定义的符号变量

1） 导数：diff(f)是求函数f对符号变量 x（或字母表上最接近字母x的符号变量求导）；而diff(f,t)是求函数f 对t 的导数。如：

f=sin(a*x);g=diff(f)

g =

cos(a*x)*a

f=sin(y*t);g=diff(f)

g =

cos(y*t)*t

f=sin(y*t);g=diff(f,t) %这可以看作二元函数求偏导数

g =

cos(y*t)*y

对于上面的f还可以用dif(f,2)求二阶导数：

f=sin(a*x);diff(f,2)

ans =

-sin(a*x)*a^2

diff(f,a,2)

ans =

-sin(a*x)*x^2

当微分运算作用于符号矩阵时，是作用于矩阵的每个元素，如：

A=[sin(a*x),cos(a*x);-cos(a*x),-sin(a*x)],dy=diff(A)

A =

[ sin(a*x), cos(a*x)]

[ -cos(a*x), -sin(a*x)]

dy =

[ cos(a*x)*a, -sin(a*x)*a]

[ sin(a*x)*a, -cos(a*x)*a]

2） 积分：int(f)是求函数f对符号变量 x（或字母表上最接近字母x的符号变量）的不定积分；而int(f,t)是求函数f 对t 的不定积分。如：

f=sin(a*x);g=int(f)

g =

-1/a*cos(a*x)

f=sin(a*x);g=int(f,a)

g =

-1/x*cos(a*x)

f=sin(x^3);g=int(f)

g =

1/6*pi^(1/2)*2^(1/3)*(3/4/pi^(1/2)*x*2^(2/3)*sin(x^3)-9/4/pi^(1/2)*x*2^(2/3)*(cos(x^3)*x^3-sin(x^3))-3/4/pi^(1/2)*x^7*2^(2/3)/(x^3)^(11/6)*sin(x^3)*LommelS1(5/6,3/2,x^3)+9/4/pi^(1/2)*x^7*2^(2/3)/(x^3)^(17/6)*(cos(x^3)*x^3-sin(x^3))*LommelS1(11/6,1/2,x^3))

f=sin(x)/x;g=int(f)

g =

sinint(x)

而int(f,a,b)是函数f对符号变量 x（或字母表上最接近字母x的符号变量）求从a到b 的定积分；而int(f,t,a,b)是求函数f 对t 从a到b 的定积分,如：

f=sin(a*x);g=int(f,0,pi)

g =

-(cos(pi*a)-1)/a

f=exp(-x^2);g=int(f,0,1)

g =

1/2*erf(1)*pi^(1/2)

a=double(g)

a =

0.7468

3）极限：limit(f)当符号变量 x（或字母表上最接近字母x的符号变量）→0时函数f的极限；而limit(f,t,a)当符号变量t→a时的极限。如：

f=sin(x)/x;g=limit(f)

g =

syms a x

f=(cos(x+a)-cos(x))/a;limit(f,a,0)

ans =

-sin(x)

syms x t

limit((1+x/t)^t,t,inf)

ans =

exp(x)

下面的例子说明求左极限和右极限的方法：

limit(1/x)

ans =

NaN

limit(1/x,x,0,'left')

ans =

-inf

limit(1/x,x,0,'right')

ans =

inf

4） 级数和：symsum(s,t,a,b)表达式s中的符号变量t从a 到b的级数和（t缺少时设定为x或最接近x 的字母），如：

symsum(1/x,1,3)

ans =

11/6

syms k

s1=symsum(1/x^2,1,inf),s2=symsum(x^k,k,0,inf)

s1 =

1/6*pi^2

s2 =

-1/(x-1)

5）泰勒多项式：taylor(f,n,a)函数f对符号变量 x（或字母表上最接近字母x的符号变量）在点a的n-1阶泰勒多项式（n缺少时设定n为6，a缺少时设定a 为0），如：

taylor(sin(x))

ans =

x-1/6*x^3+1/120*x^5

f=log(x);s=taylor(f,4,2)

s =

log(2)+1/2*x-1-1/8*(x-2)^2+1/24*(x-2)^3

2． 解方程

1）代数方程：solve(f,t)对f 中的符号变量t解方程f=0（t缺少时设定为x或最接近 x的字母），如

syms a b c

f=a*x^2+b*x+c;s=solve(f)

s =

[ 1/2/a*(-b+(b^2-4*a*c)^(1/2))]

[ 1/2/a*(-b-(b^2-4*a*c)^(1/2))]

f=a*x^2+b*x+c;solve(f,b)

ans =

-(a*x^2+c)/x

如果要解形如f(x)=q(x)的方程，则需要用单引号把方程括起来，如：

s=solve('cos(2*x)+sin(x)=1')

s =

[ 0]

[ pi]

[ 1/6*pi]

[ 5/6*pi]

solve也可以解方程组，如：

[x,y]=solve('x^2+x*y+y=3','x^2-4*x+3=0')

x =

[ 1]

[ 3]

y =

[ 1]

[ -3/2]

即方程组的解为（1，1）和（3，-3/2）。

2）微分方程：dsolve('S','s1','s2',…,'x')其中S为方程，s1,s2为初始条件，x 为自变量，方程S中用D表示求导数，D2，D3，…表示二阶、三阶等高阶导数；初始条件缺少时给出带任意常数C1，C2，…的通解；自变量缺少时设定为t。举例如下：

dsolve('Dy=1+y^2')

ans =

tan(t+C1)

y=dsolve('Dy=1+y^2','y(0)=1','x')

y =

tan(x+1/4*pi)

x=dsolve('D2x+2*D1x+2*x=exp(t)','x(0)=1','Dx(0)=0')

x =

1/5*exp(t)+3/5*exp(-t)*sin(t)+4/5*exp(-t)*cos(t)

dsolve也可以用来解微分方程组，如：

S=dsolve('Df=3*f+4*g','Dg=-4*f+3*g')

S =

f: [1x1 sym]

g: [1x1 sym]

计算的结果返回在一个结构S中，为了看到其中f,g的值，可以用：

f=S.f,g=S.g

f =

exp(3*t)*(cos(4*t)*C1+sin(4*t)*C2)

g =

-exp(3*t)*(sin(4*t)*C1-C2*cos(4*t))

4．线性代数：MATLAB中大多数用于数值线性代数计算的命令，都可以用于符号变量线性代数物计算，如：

A=[a b c;b c a;c a b];B=[1 1 1]';x=A\B

x =

[ 1/(a+c+b)]

A1=triu(A),L=eig(A)

A1 =

[ a, b, c]

[ 0, c, a]

[ 0, 0, b]

L =

[ a+c+b]

[ (-b*a+b^2-b*c-c*a+c^2+a^2)^(1/2)]

[ -(-b*a+b^2-b*c-c*a+c^2+a^2)^(1/2)]

5．化简和代换

工具箱中提供了许多化简符号表达式的函数，具有专门用途的函数及其功能是：

collect 合并同类项

expend 将乘积展开为和式

horner 把多项式表示为秦九韶方法表示形式

factor 把多项式转换为乘积形式（因式分解）

simplify 利用各种恒等式化简代数式

请看下列：

syms x a t y

collect(x^3+2*x^2-5*x^2+4*x-3*x+12-3)

ans =

x^3-3*x^2+x+9

g=collect((1+x)*t+t*x)

g =

2*t*x+t

expand((x-1)*(x-2)*(x-3))

ans =

x^3-6*x^2+11*x-6

g=expand(cos(x+y))

g =

cos(x)*cos(y)-sin(x)*sin(y)

expand(cos(3*acos(x)))

ans =

4*x^3-3*x

horner(x^3-6*x^2+11*x-6)

ans =

-6+(11+(-6+x)*x)*x

g=horner(1.1+2.2*x+3.3*x^2)

g =

11/10+(11/5+33/10*x)*x

factor(x^3-6*x^2+11*x-6)

ans =

(x-1)*(x-2)*(x-3)

n=1:5;x=x*(ones(size(n)));

p=x.^n+1,f=factor(p)

p =

[ x+1, x^2+1, x^3+1, x^4+1, x^5+1]

f =

[ x+1, x^2+1, (x+1)*(x^2-x+1), x^4+1, (x+1)*(x^4-x^3+x^2-x+1)]

syms x

simplify((1-x^2)/(1-x))

ans =

x+1

s=simplify(sin(x)^2+cos(x)^2)

s =

q=simplify((1/a^3+6/a^2+12/a+8)^(1/3))

q =

((2*a+1)^3/a^3)^(1/3)

工具箱还为我们提供了一个强有力的的函数simple它综上所述合运用上面的函数进行化简，并找出长度最短的表达式，其命令形式有以下几种：

f=simple(S)：对表达式S进行化简，输出长度最短的表达式f

simple(S)：对表达式S进行化简，输出用各种函数化简的结果，及长度最短的表达式

[f,how]=simple(S)对表达式S进行化简，输出长度最短的表达式f,及f是哪一个函数作用的结果how

f=simple(sin(x)^2+cos(x)^2)

f =

simple((1/a^3+6/a^2+12/a+8)^(1/3))

simplify:

((2*a+1)^3/a^3)^(1/3)

radsimp:

(2*a+1)/a

combine(trig):

((1+6*a+12*a^2+8*a^3)/a^3)^(1/3)

factor:

((2*a+1)^3/a^3)^(1/3)

expand:

(1/a^3+6/a^2+12/a+8)^(1/3)

combine:

(1/a^3+6/a^2+12/a+8)^(1/3)

convert(exp):

(1/a^3+6/a^2+12/a+8)^(1/3)

convert(sincos):

(1/a^3+6/a^2+12/a+8)^(1/3)

convert(tan):

(1/a^3+6/a^2+12/a+8)^(1/3)

collect(a):

(1/a^3+6/a^2+12/a+8)^(1/3)

ans =

(2*a+1)/a

[f ,how]=simple((1/a^3+6/a^2+12/a+8)^(1/3))

f =

(2*a+1)/a

how =

radsimp

工具箱中提供了两种代换命令：

subs(S,old,new) 用符号new代替表达式S中的符号old

subexpr(S) 将表达式S中的公共部分用sigma表示

syms a b;

subs(a+b,a,4)

ans =

4+b

6．其它

工具箱中提供了50多个特殊函数，如切比雪夫（Chebyshev）正交多项式等，用mfunlist命令可以看到这些函数的列表，用mhelp <函数名>可以了解那个函数的细节；

工具箱对于数值计算提供了有理数计算方式和可变位数的浮点计算方式，用法可从下例看出：

a=1/2+1/3+1/4,a1=sym(a),a2=vpa(a,10)

a =

1.0833

a1 =

13/12

a2 =

1.083333333

用3位数字计算出方程：

的解x，y，再用6位数字计算出x与y，已知正确解为练习练习x=1,y=-1,计算结果说明什么？

[x,y]=solve('0.780*x+0.563*y=0.217','0.457*x+0.330*y=0.127')

x =

y =

-1.

a=[0.780 0.563;0.457 0.330];b=[0.217;0.127];

l=vpa(a(2,1)/a(1,1),3);

c=vpa(a(2,2)-a(1,2)*l,3);d=vpa(b(2)-b(1)*l,3);

y=vpa(d/c,3),x=vpa((b(1)-a(1,2)*y)/a(1,1),3)

y =

-1.98

x =

1.71

a=[0.780 0.563;0.457 0.330];b=[0.217;0.127];

l=vpa(a(2,1)/a(1,1),6);

c=vpa(a(2,2)-a(1,2)*l,6);d=vpa(b(2)-b(1)*l,6);

y=vpa(d/c,6),x=vpa((b(1)-a(1,2)*y)/a(1,1),6)

y =

-.997571

x =

.998247

工具箱还提供了一个非常简便的画图命令：设表达式f中只有一个符号变量。比如x，则ezplot(f,xmin,xmax)画出以x为横坐标的曲线f，x在[xmin,xmax]内，当xmin,xmax缺省时，xmin=-2*pi,xmax=2*pi，请看：

syms x

ezplot(sin(2*x))

ezplot(sin(2*x),-pi/2,pi/2)

例2 为了开拓市场，某公司对其新产品作了一系列调查，他们发现这一新产品的销量与下列事件关系密切：其一是温度，其二是上证指数，其三是广告费……为此，他们记录了下面的数据表，假设这些事件与销售量近似成线性关系，试给出这种关系的数学表达式。

解对于这个例子，我们可以把销售量作为y，并用分别表示温度、上证指数、广告费、推销人员数目、返修率。然后，利用最小二乘法就可以得到其关系表达式：

A=[39,567,10000,2, 0.20;37,679,0,3,0.15;30,346,5000,3,0.10;25,987,5000,3,0.08;

25,1101,0,4,0.07;10,1004,5000,5,0.07;15,667,0,4,0.05;5,604,10000,6,0.04];

b=[75;68;105;136;152;191;148;234];

a=A\b

a =

0.6877

0.0437

0.0049

29.6072

-447.3589

a1=[0.147;0.051;4.685;28.28;-351.839];

norm(A*a-b)

norm(A*a1-b)

ans =

16.7645

ans =

7.7607e+004

e=6; %用e表示采用的有效数字位数

a=[0.780 0.563;0.457 0.330];b=[0.217;0.127];

c=vpa(a(2,1)/a(1,1),e);

y=vpa((b(2)-b(1)*c)/(a(2,2)-a(1,2)*c),e)

x=vpa((b(1)-a(1,2)*y)/a(1,1),e)

y =

-.997571

x =

.998247

例：对，，用个节点（等分）作上述三种插值，用m(=21)个插值点（等分）作图，比较结果。其语句如下：

n=4;m=8;k=12;

x=-1:0.01:1;

y=1./(1+25*x.^2);

z=0*x;

x0=-1:2/n:1;

y0=1./(1+25*x0.^2);

z0=lagr1(x0,y0,x);

x1=-1:2/m:1;

y1=1./(1+25*x1.^2);

z1=lagr1(x1,y1,x);

x2=-1:2/k:1;

y2=1./(1+25*x2.^2);

z2=lagr1(x2,y2,x);

plot(x,y,x,z0,x,z1,x,z2,x,z,'y')

legend('f(x)','n=4','n=8','n=12')

t=[0 1.5 2 3 4.5 5.45 6 7.5 9 9.8 10.5 12 13.38 14.48];

p=[0.28 1.75 2 3.43 3.29 4 4.48 6 7.37 8 8.48 9.27 9.68 9.89];

x=0:0.01:14.48;

y=interp1(t,p,x,'spline');

plot(t,p,'o',x,y);

legend('型值点','自然样条插值')

t=[1 2 3 4 5 6 7 8 9 10 11 12]';

y=[256 201 159 61 77 40 17 25 103 156 222 345]';

E=[ones(size(t)) t t.^2];

a=E\y;

T=(0:0.1:12)';

Y=[ones(size(T)) T T.^2]*a;

plot(T,Y,'-',t,y,'*');

legend('二次曲线拟合','离散数据点')

相关推荐

Matlab总结

专栏推荐