数学归纳法论文提纲
数学归纳法论文提纲
段丽娜
数学归纳法是证明与自然数有关命题的一种方法,应用广泛.数学归纳法的应用不仅仅体现在中学数学中,在高等数学命题的证明中也起着极为重要的作用.文中通过对范德蒙德行列式的证明、二次型标准化定理的证明、数学归纳法证明数列的单调性以及用数学归纳法证明整除问题、恒等式问题以及数学归纳法与其他知识点的交汇等问题来谈一谈数学归纳法在数学命题的证明上所突出的重要应用.
中文摘要
Abstract
引言
1. 数学归纳法的历史由来。
2. 数学归纳法的定义。
3. 数学归纳法解决应用问题
3.1 代数恒等式方面的问题
3.2 几何方面的应用
3.3 排列和组合
4. 对运用数学归纳法时易错的地方进行分析(举例)
5. 运用数学归纳法的典型例题。
6. 数学归纳法的用途
7. 主要参考文献
.
第二篇:数学归纳法科研论文(刘巍老师自己写的)
长沙学院信息与计算科学系本科生科研训练
数学归纳法及其应用
系 (部): 信息与计算科学 (宋体4号)
专 业: 数学与应用数学 (宋体4号)
学 号: × × × × × (宋体4号)
学生姓名: × × × (宋体4号)
成 绩:
2013 年6 月
数学归纳法及其应用
XXX
长沙学院 信息与计算科学系, 湖南 长沙, 410022
摘要:数学归纳法是一种递归方法.本文主要总结了各种不同的数学归纳法,比如第一数学归纳法、第二数学归纳法、反向数学归纳法等,同时举例说明了不同数学归纳法在代数证明中的应用.
关键词:第一数学归纳法,第二数学归纳法,反向数学归纳法
1 引言
数学归纳法是一种递归方法,并且是人们最早掌握的递归方法之一,它沟通着有限集与无限集,使人们能以有限掌握无限,以有限次操作来把握关于无限集的某些性质,即涉及到无限集的问题.
孙宏安在文献[1]中介绍了数学归纳法的历史背景及其发展历程. 孟涣晨在文献[2]中重点介绍了第一数学归纳法,第二数学归纳法及反向数学归纳法的理论依据以及相应的表现形式. 甘继荣在文献[3]系统地对各种归纳法做了探讨,如不太熟悉的螺旋式数学归纳法与二重数学归纳法等,并给出了相应的应用.
本文主要总结了几类不同的数学归纳法以及它们相应的应用.
2 数学归纳法及其应用
数学归纳法是一种证明与正整数相关命题的特殊方法,所以它主要是用来研究与正整数相关的数学问题,我们最初在中学所接触到的数学归纳法,也就是我们现在所最为熟悉的第一数学归纳法.
2.1 第一数学归纳法
定理2.1 设有一个与正整数
设有一个与正整数 有关的命题
有关的命题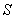 .如果(1)当
.如果(1)当 时,命题成立;(2)假设
时,命题成立;(2)假设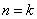 时命题也成立;(3)若能证明
时命题也成立;(3)若能证明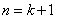 该命题也成立,则这个命题对一切正整数
该命题也成立,则这个命题对一切正整数 都成立.
都成立.
证明 假设该命题不是对于一切正整数都成立.令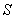 表示使命题不成立的正整数作出的集合,那么
表示使命题不成立的正整数作出的集合,那么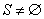 .于是由最小数原理,
.于是由最小数原理,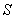 中有最小数
中有最小数 .因为命题对于
.因为命题对于 时成立,所以
时成立,所以 ,从而
,从而 是一个正整数.又由于
是一个正整数.又由于 是
是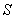 中的最小数,所以
中的最小数,所以 不属于
不属于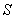 .也就是说,当
.也就是说,当 时,命题成立.于是由条件(3),当
时,命题成立.于是由条件(3),当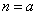 时命题也成立,因此
时命题也成立,因此 不属于
不属于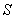 .此时与假设矛盾,因此原命题成立,即该命题对于一切正整数都成立.
.此时与假设矛盾,因此原命题成立,即该命题对于一切正整数都成立.
注 在应用数学归纳法时,有些命题不一定是从 开始的,此时在叙述上只要将条件(1)中的
开始的,此时在叙述上只要将条件(1)中的 换成
换成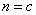 即可.
即可.
故第一数学归纳法可以概括为以下三个步骤
(1)归纳基础:证明 时命题成立;
时命题成立;
(2)归纳假设:假设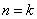 时命题成立;
时命题成立;
(3)归纳递推:由归纳假设推出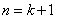 时命题也成立.
时命题也成立.
在用数学归纳法来证明一个与自然数 有关的命题时,证明过程中必须包括定理中的(1)(2)两个步骤.(1)是基础,没有这个特例做基础就不能假设当
有关的命题时,证明过程中必须包括定理中的(1)(2)两个步骤.(1)是基础,没有这个特例做基础就不能假设当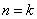 时命题
时命题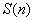 成立.同样的,步骤(2)也不可缺少,只有在(1)成立时,又能在这个基础上证明(2)成立,给这个基础以正确的无限度的自动推演,才能确定命题的一般正确性.因此,有了(1) (2)两个步骤,才能使我们的认识由有限到无限来一个飞跃.
成立.同样的,步骤(2)也不可缺少,只有在(1)成立时,又能在这个基础上证明(2)成立,给这个基础以正确的无限度的自动推演,才能确定命题的一般正确性.因此,有了(1) (2)两个步骤,才能使我们的认识由有限到无限来一个飞跃.
在了解了第一数学归纳法的原理之后,我们来看它在 级的范德蒙德行列式的证明过程中的应用.
级的范德蒙德行列式的证明过程中的应用.
例2.1
 级的范德蒙德行列式
级的范德蒙德行列式
 ,
,
证明对于任意的
 ,
, 级范德蒙德行列式等于
级范德蒙德行列式等于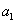 ,
,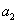 ,
, ,…,
,…, 这
这 个数的所有可能的差
个数的所有可能的差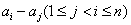 的乘积.
的乘积.
证明 对 作第一数学归纳法.
作第一数学归纳法.
(1)当 时,
时,
 ,
,
这个显然是正确的.
(2)假设对于 级的范德蒙德行列式结论成立.
级的范德蒙德行列式结论成立.
(3)现在来证明 级时的情形.
级时的情形.
对于原式,即 级的范德蒙德行列式中,第
级的范德蒙德行列式中,第 行减去第
行减去第 行的
行的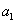 倍.也就是说由上而下地从每一行减去它上一行的
倍.也就是说由上而下地从每一行减去它上一行的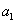 倍,得到
倍,得到

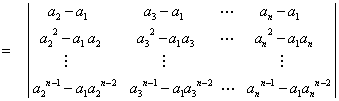
 .
.
而后面的这行列式是一个 级的范德蒙德行列式,根据数学归纳法的假设,它等于所有可能差
级的范德蒙德行列式,根据数学归纳法的假设,它等于所有可能差 的乘积,而包括
的乘积,而包括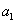 的差全在前面出现了.因此,结论对
的差全在前面出现了.因此,结论对 级范德蒙德行列式也成立.于是,根据数学归纳法完成了证明. 证毕
级范德蒙德行列式也成立.于是,根据数学归纳法完成了证明. 证毕
用连乘号,这个结果可以简写为
 ,
,
即 级的范德蒙德行列式等于
级的范德蒙德行列式等于 这
这 个数所有可能差
个数所有可能差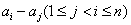 的乘积.
的乘积.
2.2 第二数学归纳法
第一数学归纳法是假设在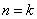 的时候成立,它可以应用的证明之中的假定较弱,仅仅需要
的时候成立,它可以应用的证明之中的假定较弱,仅仅需要 成立来证明
成立来证明 也成立即可,如很多关于等式成立和数列通项公式成立证明,而在有些情况中,仅仅假设
也成立即可,如很多关于等式成立和数列通项公式成立证明,而在有些情况中,仅仅假设 成立来证明
成立来证明 也成立是不够的,还需要较强的假定,还需要前面各步都要成立,这种加强了的归纳法就形成了第二数学归纳法.
也成立是不够的,还需要较强的假定,还需要前面各步都要成立,这种加强了的归纳法就形成了第二数学归纳法.
定理2.2 设一个与正整数
设一个与正整数 有关的命题
有关的命题 .如果(1)当
.如果(1)当 时命题成立;(2)再假设命题对于一切正整数
时命题成立;(2)再假设命题对于一切正整数 成立时;(3)若能证明
成立时;(3)若能证明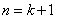 该命题也成立,则这个命题对一切正整数
该命题也成立,则这个命题对一切正整数 都成立.
都成立.
证明的方法与第一数学归纳法的证明方法完全类似,同样运用反证法即可以证明得出.
证明 假设命题 不是对一切正整数都成立.令
不是对一切正整数都成立.令 表示使命题不成立的正整数作出的集合,那么
表示使命题不成立的正整数作出的集合,那么 .于是由最小数原理,
.于是由最小数原理, 中含有一个最小数
中含有一个最小数 ,并且
,并且 ,所以对一切
,所以对一切 ,命题
,命题 成立,又由(2)(3)推出
成立,又由(2)(3)推出 对
对 正确,故结论矛盾,原命题成立.
正确,故结论矛盾,原命题成立.
第二数学归纳法的也可以概括为以下三个步骤:
(1)归纳基础:证明 时命题成立;
时命题成立;
(2)归纳假设:假设当 时,命题成立;
时,命题成立;
(3)归纳递推:由归纳假设推出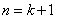 时命题也成立.
时命题也成立.
从第一数学归纳法和第二数学归纳法的定理来看,第二数学归纳法与第一数学归纳法基本形式的区别就在于归纳假设.
在了解第二数学归纳法的原理后,我们看一个例题,来更加直观生动地观察出它与第一数学归纳法的区别之处.
例2.2 已知任意自然数 均有
均有
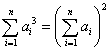 ,(这里
,(这里 )
)
求证 .
.
证明 (1)当 时,由
时,由 ,得
,得 ,
,
所以命题对 正确.
正确.
(2)假设对 命题正确,这时
命题正确,这时
 ,
, ,
, ,
, .
.
(3)当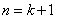 时,
时,
 , (2.1)
, (2.1)
但是

 , (2.2)
, (2.2)
又因为归纳假设对 命题正确,所以
命题正确,所以
 ,
, ,
, ,
, ,
,
所以
 .
.
由(2.1)和(2.2)式得
 ,
,
消去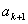 ,得
,得
 ,
,
解得
 (
(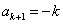 舍去),
舍去),
所以命题对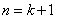 也正确.
也正确.
由例2.2, 我们可以看到它只假设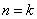 成立,即
成立,即 ,显然是不够的,需要归结到
,显然是不够的,需要归结到 时,由此可见,第一数学归纳法与第二数学归纳法的实质是等价的,第二数学归纳法包含第一数学归纳法,但是此处第二数学归纳法的作用是不能由第一归纳法所替代的.
时,由此可见,第一数学归纳法与第二数学归纳法的实质是等价的,第二数学归纳法包含第一数学归纳法,但是此处第二数学归纳法的作用是不能由第一归纳法所替代的.
为了进一步了解它们的区别,我们来看看带余除法的证明过程.
例2.3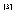 对于
对于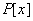 中任意两个多项式
中任意两个多项式 与
与 ,其中
,其中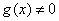 ,一定有
,一定有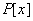 中的多项式
中的多项式 ,
,  存在,使
存在,使
 (2.3)
(2.3)
成立,其中 或者
或者 .
.
证明 (2.3)中 和
和 的存在性可以由上面所说的除法直接得出.我们用归纳法的语言来进行叙述.
的存在性可以由上面所说的除法直接得出.我们用归纳法的语言来进行叙述.
如果 ,取
,取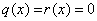 即可 .
即可 .
以下设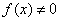 .令
.令 ,
,  的次数分别为
的次数分别为 ,
,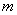 .对
.对 的次数
的次数 作第二数学归纳法.
作第二数学归纳法.
当 时,显然取
时,显然取 ,
, ,(1)式成立.
,(1)式成立.
下面来讨论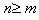 的情形.假设当次数小于
的情形.假设当次数小于 时,
时,  ,
, 的存在已证.现在看次数为
的存在已证.现在看次数为 的情形.
的情形.
令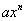 ,
, 分别是
分别是 ,
, 的首项,显然
的首项,显然 与
与 有相同的首项,因而多项式
有相同的首项,因而多项式

的次数小于 或为0.对于后者,取
或为0.对于后者,取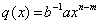 ,
, ;对于前者,由归纳法假设,对
;对于前者,由归纳法假设,对 ,
, 有
有 ,
, 存在使得
存在使得
 ,
,
其中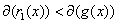 或者
或者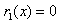 .于是
.于是
 ,
,
也就是说,有 ,
,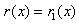 使得
使得

成立.由归纳法原理,对任意的 ,
,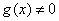 ,
, ,
, 的存在性就证明了.
的存在性就证明了.
下面来看一个具体的例子:令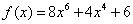 ,
, ,得到
,得到
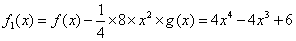 ,
,
由此,我们可以看到如果按照第一数学归纳法 的次数应该是5,故第一数学归纳法在此是不适用的.
的次数应该是5,故第一数学归纳法在此是不适用的.
2.3 反向数学归纳法
第一数学归纳法和第二数学归纳法两种情形,都是从命题对较小的自然数成立来推出命题对较大的自然数也成立.但是在有些情况下,正向推进证明比较困难,此时推理的方向可以反过来,就如数学证明中的反证法一样,可以使得一些证明会更加简捷,具体对于数学归纳法的证明步骤来说,即从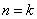 时成立推出
时成立推出 时成立.这样的数学归纳法就称之为反向数学归纳法,又叫倒推数学归纳法.
时成立.这样的数学归纳法就称之为反向数学归纳法,又叫倒推数学归纳法.
定理2.3 设有一个与正整数
设有一个与正整数 有关的命题
有关的命题 .如果(1)命题
.如果(1)命题 对无限多个正整数
对无限多个正整数 成立;(2)假设
成立;(2)假设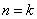 时命题成立;(3)若能证明
时命题成立;(3)若能证明 该命题也成立,则这个命题对一切正整数
该命题也成立,则这个命题对一切正整数 都成立.
都成立.
证明 运用反证法.假设该命题不是对于一切正整数 都成立.令
都成立.令 表示使命题不成立的正整数构成的集合,那么
表示使命题不成立的正整数构成的集合,那么 .任取
.任取 ,由条件(1)可知必有正整数
,由条件(1)可知必有正整数 ,使
,使 成立.令由这样的正整数
成立.令由这样的正整数 组成的集合为
组成的集合为 ,因为集合
,因为集合 ,故必有最小数,设为
,故必有最小数,设为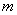 ,显然
,显然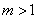 .由条件(3)可知,
.由条件(3)可知,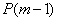 成立,由
成立,由 的取法可知
的取法可知 ,但是这与
,但是这与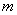 的最小性质相矛盾.
的最小性质相矛盾.
反向数学归纳法由法国数学家柯西首创,它可以概括为以下三个步骤:
(1)归纳基础:证明命题对无限多个正整数 成立;
成立;
(2)归纳假设:假设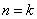 时命题成立;
时命题成立;
(3)归纳递推:由归纳假设推出 时命题也成立.
时命题也成立.
在理解反向数学归纳法的原理基础之上,我们来看一个经典的不等式的证明过程中反向归纳法的应用.
例2.4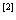 求证
求证 个正实数的算术平均值大于或等于这
个正实数的算术平均值大于或等于这 个数的几何平均值,即
个数的几何平均值,即
 .
.
证明 (1)当 时,
时,
 ,
,
因此命题对 正确.
正确.
当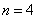 时,
时,
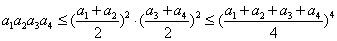 ,
,
因此命题对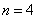 正确.
正确.
同理可推出命题对 ,
, ,…,
,…, ,…都正确(
,…都正确( 为任意自然数),所以命题对无穷多个自然数成立.
为任意自然数),所以命题对无穷多个自然数成立.
(2)设命题对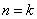 正确,令
正确,令
 ,
,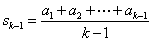 ,
,
则 .
.
(3)由归纳假设命题对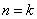 正确,所以
正确,所以
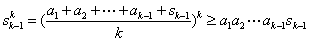 ,
,
所以

 ,
,
即
 ,
,
命题对 也正确,由反向归纳法原理知,命题对一切自然数成立. 证毕
也正确,由反向归纳法原理知,命题对一切自然数成立. 证毕
参考文献
[1] 孙宏安.数学归纳法的历史[J].中学数学教学参考,1999,(1):125.
[2] 孟涣晨.数学归纳法及其应用[J].教学园地,2009:119.
[3] 甘继荣.数学归纳法种种[J].云梦学刊,1982:16-24.
- 优秀论文提纲范文
-
论文提纲怎么写?
黑龙江英才网论文提纲怎么写论文提纲可分为简单提纲和详细提纲两种简单提纲是高度概括的只提示论文的要点如何展开则不涉及这种提纲虽然简单…
-
毕业论文提纲范文
毕业论文提纲范文时间20xx01271221毕业论文提纲范文简单点说写毕业论文不外乎是资料的查找论文题目的确定360期刊网为大家提…
-
论文提纲范文
房地产企业成本管理分析内容摘要摘要房地产项目开发是一项综合性很强的经济活动许多房地产开发公司在项目开发过程中由于缺乏系统的成本控制…
-
汉语言文学专业毕业论文提纲
四川省高等教育自学考试汉语言文学专业本科毕业论文提纲题目浅析行政公文的语言艺术指导教师马容准考证号37220xx00076考生姓名…
-
数学归纳法总结
【数学归纳法】【数学归纳法的基本形式】1.第一数学归纳法设P(n)是一个与正整数有关的命题,如果①当n?n0(n0?N)时,P(n…
-
求极限的方法总结 小论文
求数列极限的方法总结数学科学学院数学与应用数学08级汉班指导教师摘要数列极限的求法一直是数列中一个比较重要的问题本文通过归纳和总结…
-
探秘议论文归纳法与反面假设法的运用
探秘议论文归纳法与反面假设法的运用摘要受先前话题作文等的影响在高中生的议论文习作中具有规范的内涵较为丰富的有思辨和哲理的议论文依然…
-
本科毕业论文---浅谈数学归纳法的应用
浅谈数学归纳法的应用摘要数学归纳法是数学上证明与自然数N有关的命题的一种常用的方法它主要用来研究与正整数有关的数学问题基本思想就是…
-
数学归纳法论文
目录一绪论2二不完全归纳法和完全归纳法3三归纳法的基本形式3四数学归纳法证明恒等式4五应用数学归纳法证明不等式5六数学归纳法证明整…