泛函分析总结
泛函分析知识点小结及应用
§1 度量空间的进一步例子
设 是任一非空集合,若对于
是任一非空集合,若对于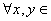
 ,都有唯一确定的实数
,都有唯一确定的实数 与之对应,且满足
与之对应,且满足
1.非负性:
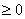 ,
, =0
=0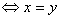 ;
;
2. 对称性:d(x,y)=d(y,x);
3.三角不等式:对
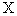 ,都有
,都有
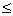
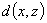 +
+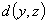 , 则称(
, 则称(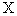 ,
,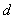 )为度量空间,
)为度量空间,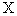 中的元素称为点。
中的元素称为点。
欧氏空间 对
对 中任意两点
中任意两点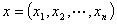 和
和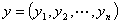 ,规定距离为
,规定距离为  =
=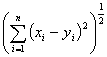 .
.
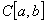 空间
空间 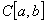 表示闭区间
表示闭区间 上实值(或复值)连续函数的全体.对
上实值(或复值)连续函数的全体.对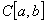 中任意两点
中任意两点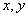 ,定义
,定义 =
=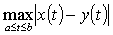 .
.
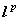 (
(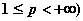 空间 记
空间 记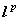 =
=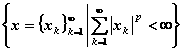 .
.
设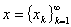 ,
,
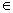
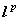 ,定义
,定义  =
=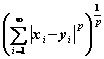 .
.
例1 序列空间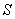
令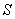 表示实数列(或复数列)的全体,对
表示实数列(或复数列)的全体,对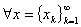 ,
, ,令
,令
 =
=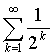
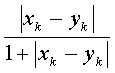 .
.
例2 有界函数空间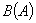
设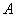 是一个给定的集合,令
是一个给定的集合,令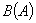 表示
表示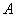 上有界实值(或复值)函数的全体.
上有界实值(或复值)函数的全体. 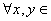
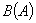 ,定义
,定义  =
=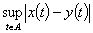 .
.
例3 可测函数空间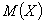
设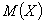 为
为 上实值(或复值)的可测函数的全体,
上实值(或复值)的可测函数的全体,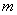 为Lebesgue测度,若
为Lebesgue测度,若
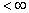 ,对任意两个可测函数
,对任意两个可测函数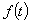 及
及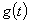 ,由于
,由于 ,故不等式左边为
,故不等式左边为 上可积函数. 令
上可积函数. 令  =
=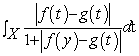 .
.
§2 度量空间中的极限
设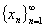 是
是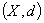 中点列,若
中点列,若 ,s.t.
,s.t.
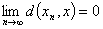 (
(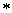 )
)
则称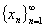 是收敛点列,
是收敛点列,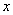 是点列
是点列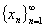 的极限.
的极限.
收敛点列的极限是唯一的. 若设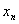 既牧敛于
既牧敛于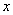 又收敛
又收敛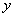 ,则因为
,则因为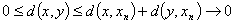
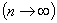 ,而有
,而有  =0. 所以
=0. 所以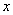 =
=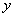 .
.
注 (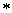 )式换一个表达方式:
)式换一个表达方式: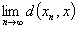 =
=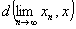 . 即当点列极限存在时,距离运算与极限运算可以换序. 更一般地有
. 即当点列极限存在时,距离运算与极限运算可以换序. 更一般地有
距离 是
是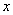 和
和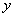 的连续函数.
的连续函数.
具体空间中点列收敛的具体意义:
1. 欧氏空间
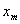 =
=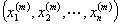 ,
,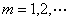 ,为
,为 中的点列,
中的点列,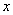 =
=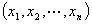
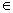
 ,
, 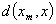 =
=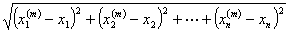 .
. 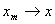
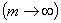
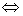 对每个
对每个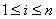 ,有
,有 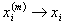
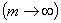 .
.
2. 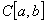 设
设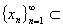
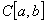 ,
,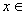
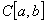 ,则
,则 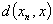 =
=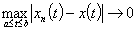
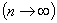
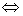
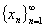 在
在 一致收敛于
一致收敛于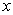 .
.
3. 序列空间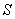 设
设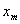 =
=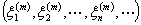 ,
,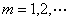 ,及
,及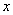 =
=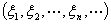 分别是
分别是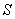 中的点列及点,则
中的点列及点,则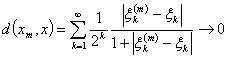
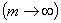
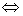
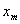 依坐标收敛于
依坐标收敛于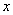 .
.
4. 可测函数空间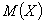 设
设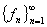
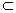
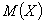 ,
,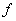
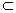
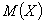 ,则因
,则因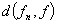 =
=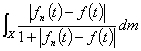 ,有
,有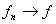
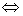
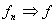 .
.
§3 度量空间中的稠密集 可分空间
定义 设 是度量空间,
是度量空间,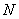 和
和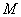 是
是 的两个子集,令
的两个子集,令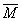 表示
表示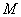 的闭包,若
的闭包,若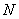
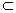
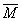 ,则称集
,则称集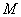 在集
在集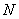 中稠密,当
中稠密,当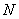 =
= 时,称
时,称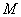 为
为 的一个稠密子集. 若
的一个稠密子集. 若 有一个可数的稠密子集,则称
有一个可数的稠密子集,则称 是可分空间. 例1
是可分空间. 例1  维欧氏空间
维欧氏空间 是可分空间. 事实上,坐标为有理数的点的全体是
是可分空间. 事实上,坐标为有理数的点的全体是 的可数稠密子集. 例2 离散距离空间
的可数稠密子集. 例2 离散距离空间 可分
可分 
 是可数集. 例3
是可数集. 例3  是不可分空间.
是不可分空间.
§4 连续映射
定义 设 =
=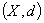 ,
,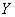 =
=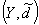 是两个度量空间,
是两个度量空间,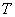 是
是 到
到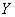 中的映射:
中的映射: =
=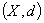
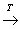
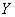 =
=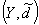 .
. 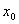
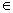
 ,若
,若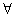
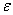
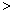 0,
0,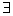
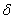
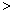 0,s.t.
0,s.t. 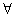
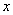
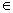
 且
且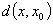
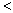
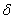 ,都有
,都有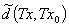
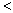
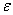 ,则称
,则称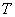 在
在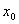 连续:
连续:
定理 1 设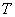 是度量空间
是度量空间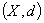 到度量空间
到度量空间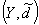 中的映射:
中的映射: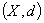
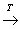
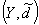 , 则
, 则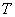 在
在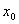 连续
连续 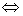 当
当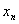
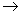
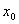 时,必有
时,必有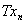
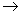
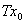 .
.
定理2 度量空间 到
到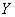 中的映照
中的映照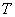 是
是 上的连续映射
上的连续映射 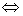 任意开集
任意开集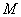
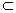
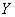 ,
,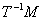 是
是 中的开集.
中的开集.
定理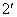 度量空间
度量空间 到
到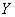 中的映照
中的映照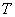 是
是 上的连续映照
上的连续映照 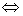 任意闭集
任意闭集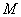
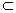
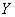 ,
,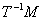 是
是 中的闭集.
中的闭集.
§5 柯西点列和完备度量空间
定义 1 设 =(
=( ,
,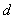 )是度量空间,
)是度量空间,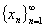 是
是 中的点列. 若
中的点列. 若 0,
0,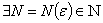 ,s.t.当
,s.t.当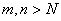 时,有
时,有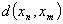
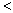
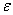 ,则称
,则称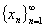 是
是 中的柯西点列或基本点列. 若度量空间(
中的柯西点列或基本点列. 若度量空间( ,
,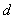 )中每个柯西点列都收敛,则称(
)中每个柯西点列都收敛,则称( ,
,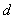 )是完备的度量空间.
)是完备的度量空间.
在一般空间中,柯西点列不一定收敛,如点列1, 1.4, 1,41, 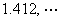 在
在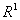 中收敛于
中收敛于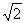 ,在有理数集中不收敛.
,在有理数集中不收敛.
但度量空间中每一个收敛点列都是柯西点列.
定理1 完备度量空间 的子空间
的子空间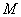 是完备度量空间
是完备度量空间 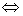
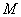 是
是 中的闭子空间.
中的闭子空间.
常见例子:(1)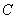 (收敛的实或复数列的全体)是完备度量空间
(收敛的实或复数列的全体)是完备度量空间
(2) 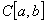 是完备的度量空间
是完备的度量空间
(3) 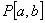 (实系数多项式全体)是不完备的度量空间
(实系数多项式全体)是不完备的度量空间
§6 度量空间的完备化
定义 1 设( ,
,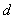 ),(
),(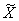 ,
,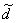 )是两个度量空间,若存在
)是两个度量空间,若存在 到
到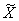 上的保距映射
上的保距映射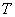 (
(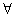
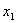 ,
,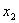
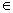
 ,有
,有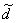 (
(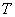
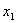 ,
,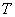
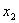 )=
)=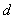 (
(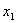 ,
,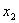 )),则称(
)),则称( ,
,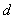 )和(
)和(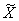 ,
,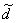 )等距同构,此时称
)等距同构,此时称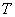 为
为 到
到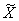 上的等距同构映照。等距同构映照是1-1映射.
上的等距同构映照。等距同构映照是1-1映射.
定理1 (度量空间的完备化定理) 设 =(
=( ,
,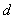 )是度量空间,那么一定存在一完备度量空间
)是度量空间,那么一定存在一完备度量空间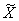 =(
=(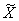 ,
,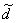 ),使
),使 与
与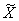 的其个稠密子空间
的其个稠密子空间 等距同构,并且
等距同构,并且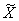 在等距同构意义下是唯一的,即若(
在等距同构意义下是唯一的,即若(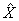 ,
,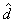 )也是一完备度量空间,且
)也是一完备度量空间,且 与
与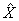 的其个稠密子空间
的其个稠密子空间 等距同构,则(
等距同构,则(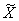 ,
,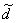 )与(
)与(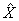 ,
,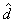 )等距同构.
)等距同构.
§7压缩映照原理及其应用
定义 设 是度量空间,
是度量空间,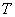 是
是 到
到 中的压映照,若存在一个数
中的压映照,若存在一个数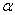 :0
:0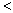
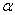
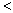 1,s.t.
1,s.t. 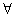
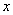 、
、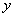
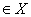 ,成立
,成立 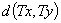
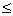
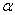

则称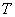 是
是 到
到 中的压缩映照(简称压缩映照).
中的压缩映照(简称压缩映照).
定理1.(压缩映射定理) 设 是完备度量空间,
是完备度量空间,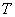 是
是 上的压缩映照,则
上的压缩映照,则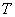 有且只有一个不动点(即方程
有且只有一个不动点(即方程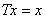 有且只有一个解).
有且只有一个解).
补充定义:若TX=X,则称X是T的不动点,即X是T的不动点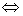 X是方程TX=X的解。
X是方程TX=X的解。
定理2. 设函数 在带状域
在带状域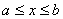 ,
,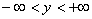 中处处连续,且处处有关于
中处处连续,且处处有关于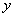 的偏导数
的偏导数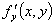 ,若存在常数
,若存在常数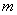 和
和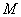 , 满足
, 满足 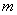
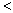
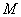 ,0
,0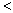
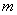
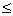
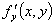
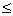
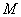 , 则方程
, 则方程  =0 在区间
=0 在区间 上必有唯一的连续函数
上必有唯一的连续函数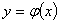 作为解:
作为解: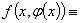 0,
0,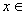
 .
.
§8赋范线性空间和Banach空间
线性空间+范数Þ线性赋范空间线性赋范空间+完备性Þ巴拿赫空间
定义1 设X是任一非空集合,若K是一个数域(R或C),如果X对某种规定的加法和数乘两种运算封闭,且"x,y,zÎX, l,ÎmK, 满足:
1) x+y=y+x (加法交换律)
2) (x+y)+z+x+(x+y) (加法结合律)
3) Îq$X, 使x+q=x (零元素存在性)
4) $x’ÎX,使x+x’=q (逆元存在性)
5) l(mx)=mlx=m(lx) (数乘结合律)
6) 1x=x, 0x=q
7) (l+m)x=lx+mx (元素对数的加法分配律)
8) l(x+y)=lx+ly (数对元素的加法分配律)
则称x+y为x与y的和,lx为数l与x的数乘 , 称X为线性空间或向量空间 (实或复),X中的元素称为向量。
定义(范数,赋范线性空间) 设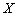 为是实(或复)数域
为是实(或复)数域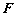 的线性空间,若对
的线性空间,若对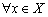 ,存在一个实数
,存在一个实数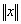 于之对应,且满足下列条件:
于之对应,且满足下列条件:
(1) 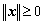 ; 且
; 且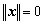
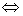
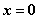 ; (非负性)
; (非负性)
(2) 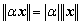 ,
,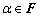 ; (正齐(次)性)
; (正齐(次)性)
(3) 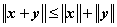 ,
,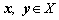 ; (三角不等式)
; (三角不等式)
则称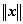 为
为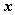 的范数(norm),称
的范数(norm),称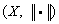 (或:
(或: )为赋范线性空间
)为赋范线性空间
定义 完备的赋范线性空间称为巴拿赫(Banach)空间。
例子: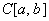 ,空间
,空间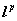 ,
,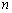 维Euclidean空间
维Euclidean空间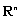 ,
, ,
,
都是Banach空间。
度量空间与赋范线性空间 区别:度量空间是定义了度量的线性空间,也就是两个元素之间的“长度”,满足非负性、对称性、三角不等式。赋范线性空间就是定义了范数的线性空间,其满足范数公理(非负性,齐次性,三角不等式)
联系:都是在线性空间的前提下讨论的。赋范线性空间是一种特殊的度量空间
第二篇:泛函分析复习与总结
《泛函分析》复习与总结
(20##年6月26日星期四 10:20---11:50)
第一部分空间及其性质
泛函分析的主要内容分为空间和算子两大部分. 空间包括泛函分析所学过的各种抽象空间, 函数空间, 向量空间等, 也包括空间的性质, 例如完备性, 紧性, 线性性质, 空间中集合的各种性质等等。以下几点是对第一部分内容的归纳和总结。
一.空间
(1)距离空间 (集合+距离)
!验证距离的三个条件: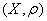 称为是距离空间,如果对于
称为是距离空间,如果对于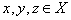
(i) 【非负性】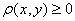 ,并且
,并且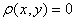 当且仅当
当且仅当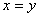 【正定性】;
【正定性】;
(ii) 【对称性】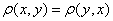 ;
;
(iii) 【三角不等式】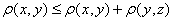 。
。
距离空间的典型代表: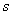 空间、
空间、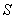 空间、所有的赋范线性空间、所有的内积空间。
空间、所有的赋范线性空间、所有的内积空间。
(2)赋范线性空间 (线性空间 + 范数)
!验证范数的三个条件: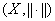 称为是赋范线性空间,如果
称为是赋范线性空间,如果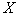 是数域
是数域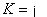 (或
(或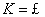 )上的线性空间,对于
)上的线性空间,对于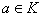 和
和 ,成立
,成立
(i) 【非负性】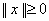 ,并且
,并且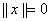 当且仅当
当且仅当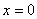 【正定性】;
【正定性】;
(ii) 【齐次性】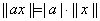 ;
;
(iii) 【三角不等式】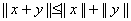 。
。
赋范线性空间的典型代表: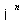 空间(
空间(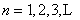 )、
)、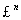 空间(
空间(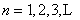 )、
)、 空间(
空间(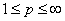 )、
)、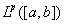 空间(
空间(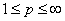 )、
)、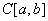 空间、
空间、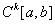 空间、Banach空间、所有的内积空间(范数是由内积导出的范数)。
空间、Banach空间、所有的内积空间(范数是由内积导出的范数)。
(3)内积空间 (线性空间 + 内积)
!验证内积的四个条件: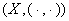 称为是内积空间,如果
称为是内积空间,如果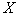 是数域
是数域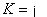 (或
(或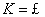 )上的线性空间,对于
)上的线性空间,对于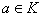 和
和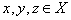 ,成立
,成立
(i) 【非负性】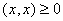 ,并且
,并且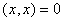 当且仅当
当且仅当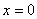 【正定性】;
【正定性】;
(ii) 【第一变元可加性】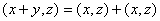 ;
;
(iii) 【第一变元齐次性】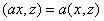 ;
;
(iv) 【共轭对称性】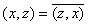 。
。
内积空间的典型代表: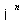 空间(
空间(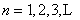 )、
)、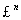 空间(
空间(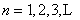 )、
)、 空间、
空间、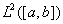 空间。
空间。
注. 1) 从概念的外延来理解, 有如下的关系:
{内积空间}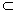 {赋范线性空间}
{赋范线性空间}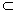 {距离空间}.
{距离空间}.
2) 内积可导出范数, 范数可导出距离, 反之未必. 例如在赋范线性空间中, 如果范数满足平行四边形公式, 则由范数可以定义内积.
3) 在距离空间中,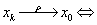
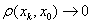 ,当
,当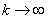 ;
;
赋范线性空间中,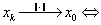
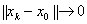 ,当
,当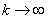 ;
;
内积空间中, 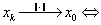
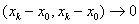 ,当
,当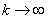 .
.
重点.!要求会验证距离, 范数和内积.
二.完备性,稠密性,可分性
(1)!完备性
距离的完备性是指“空间中的任何基本列都是收敛的”
具有完备性的距离空间称为完备距离空间;完备的赋范线性空间称为Banach空间;完备的内积性空间称为Hilbert空间.
重点. 验证一个距离是否完备是泛函分析基本的技能。
注. 距离空间的*完备化不是本课程的重点.
(2)稠密性
若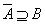 , 则称
, 则称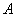 在
在 中稠密. 当
中稠密. 当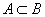 时, 也称
时, 也称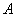 是
是 的稠密子集.
的稠密子集.
关于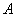 在
在 中稠密的等价命题:
中稠密的等价命题:
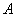 在
在 中稠密
中稠密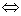
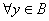 , 存在
, 存在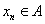 , 使得
, 使得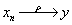 ;
;
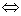
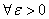 ,
, 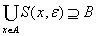 .
.
(3)!可分性
如果 有可数的稠密子集
有可数的稠密子集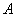 , 则称
, 则称 具有可分性. 类似地可以定义可分的距离空间, 可分的赋范线性空间, 可分的内积空间等. 不具有可分性的空间
具有可分性. 类似地可以定义可分的距离空间, 可分的赋范线性空间, 可分的内积空间等. 不具有可分性的空间 称为不可分空间.
称为不可分空间.
可分空间的典型代表: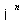 空间(
空间(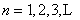 )、
)、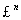 空间(
空间(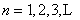 )、
)、 空间(
空间( )、
)、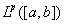 空间(
空间( )、
)、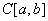 空间、
空间、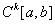 空间.
空间.
不可分空间的典型代表: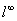 空间、
空间、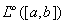 空间.
空间.
重点. 要求会找出具体的可分空间中可数稠子集. 掌握不可分空间的证明方法.
!不可分空间的证明方法: 如果空间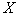 中含有一个不可数子集
中含有一个不可数子集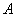 , 且其中任何两个不同点之间的距离大等于一个确定的正数, 则
, 且其中任何两个不同点之间的距离大等于一个确定的正数, 则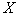 是不可分的. (例如
是不可分的. (例如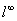 中这样的集合是分量为零和1的无穷维向量全体;
中这样的集合是分量为零和1的无穷维向量全体;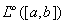 中这样的集合是
中这样的集合是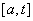 上的集特征函数全体)
上的集特征函数全体)
三 空间中的集合
(1)开集、闭集、有界集、无界集;
(2)疏朗集、稠密集;
(3)列紧集!、完全有界集!、紧集.
具体空间中列紧集的判别条件:
a.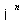 和
和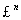 或有限维赋范线性空间中:Weierstrass定理(有界集是列紧集);
或有限维赋范线性空间中:Weierstrass定理(有界集是列紧集);
b. !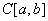 中: Arzela-Ascoli定理(一致有界且等度连续);
中: Arzela-Ascoli定理(一致有界且等度连续);
(4)内积空间中的正交集, !正交基.
Parseval恒等式、Bessel不等式。
(5)有限维赋范线性空间的性质:
1. 有界集即列紧集;
2. 有限维赋范线性空间中任何两个范数都是等价的。
四 具体的空间
已经学过的具体空间有:
u 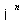 空间(
空间(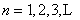 );
);
u 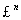 空间(
空间(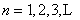 );
);
u  空间(
空间(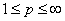 );
);
u 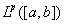 空间(
空间(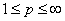 );
);
u 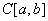 空间;
空间;
u 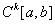 空间。
空间。
注. 1. 要求掌握每个具体空间中收敛的含义;(例如有限维赋范线性空间中点列按范数收敛意味着每个分量收敛、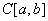 点列的收敛意味着函数列的一致收敛等等)。
点列的收敛意味着函数列的一致收敛等等)。
2. !要求掌握列紧集的判别方法(仅限于有限维赋范线性空间中Weierstrass定理和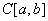 空间中的Arzela-Ascoli定理);
空间中的Arzela-Ascoli定理);
3. !要求掌握具体空间中距离或范数完备性的证明方法;(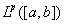 的完备性证明不作要求)
的完备性证明不作要求)
4. 会用Holder不等式、Minkowski不等式、Cauchy不等式、Schwartz不等式和Bessel不等式等;
5. 具体空间的共轭空间, 仅限于要求掌握:
! 空间(
空间(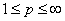 )的共轭空间(泛函的表示形式,等距同构,证明不作要求);
)的共轭空间(泛函的表示形式,等距同构,证明不作要求);
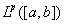 空间(
空间(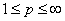 )的共轭空间(泛函的表示形式,等距同构,证明不作要求);
)的共轭空间(泛函的表示形式,等距同构,证明不作要求);
第二部分映射算子泛函
泛函分析的主要内容分为空间和算子两大部分. 算子部分包括泛函分析所学过的各种抽象或具体的映射,算子,泛函等。也涉及到与之相关的性质和众多重要的定理, 例如共鸣定理,闭图像定理,开映射定理以及泛函延拓定理等等。以下几点是对第二部分内容的归纳和总结。
一. 泛函分析中的映射
在泛函分析中, 映射
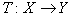
当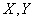 是空间时称为算子; 当
是空间时称为算子; 当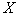 是空间,
是空间, 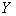 是数域(
是数域(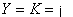 或
或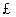 )时称为泛函;
)时称为泛函;
当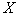 是线性空间时, 主要考虑线性算子:
是线性空间时, 主要考虑线性算子:
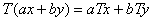 ,
, 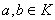 ,
,  ;
;
泛函分析中的非线性映射:
1. *压缩映射: 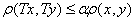 , 其中
, 其中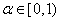 . Banach不动点定理.
. Banach不动点定理.
2. *紧集上的连续泛函(对照数学分析中有限闭区间上的连续函数的性质).
二. 有界线性算子
(1) 是由
是由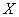 映射到
映射到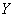 的有界线性算子全体所组成的赋范线性空间(尤其是当
的有界线性算子全体所组成的赋范线性空间(尤其是当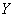 是Banach空间时
是Banach空间时 也是Banach空间);
也是Banach空间);
(2)有界线性算子列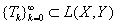 的收敛:
的收敛:
算子列的按算子范数收敛: 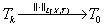 ;
;
算子列的强收敛: 对于每一个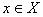 ,
,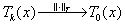 ;
;
(参见Banach-Steinhaus定理,P59)
(3)重要定理
开映射定理、逆算子定理;
!共鸣定理、 !一致有界定理、 !Banach-Steinhaus定理;
闭图像定理、
!范数等价性定理(P63引理1);
注. 重点在于定理的理解和应用,定理的证明通常不作要求。
(4)共轭算子 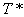
共轭算子的定义(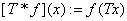 )以及简单性质;
)以及简单性质;
重要实例:*以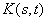 为核的积分算子的共轭算子、 !左位移(右位移)算子的共轭算子。
为核的积分算子的共轭算子、 !左位移(右位移)算子的共轭算子。
(5)具体的线性算子
l !以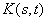 为核的积分算子;
为核的积分算子;
l !由变上限积分所定义的算子;
l 微分算子;
l !由 到
到 的左位移(右位移)算子.
的左位移(右位移)算子.
注. 线性算子的有界性等价于连续性.
重点. 要求掌握:验证算子有意义、验证线性性质、验证线性算子是有界的、 !会求较为简单的算子或泛函的算子范数。
三. 有界线性泛函
(1)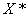 的概念和简单性质 (
的概念和简单性质 (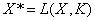 ).
).
(2) 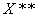 的概念和简单性质: 在等距同构(自然投射)的意义下
的概念和简单性质: 在等距同构(自然投射)的意义下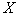 可以视为
可以视为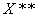 的子空间(
的子空间(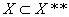 ),当在等距同构意义下
),当在等距同构意义下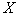 与
与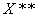 相等时,称为自反空间;
相等时,称为自反空间;
(3)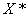 的实例:!
的实例:! 空间(
空间(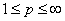 )的共轭空间(泛函的表示形式,等距同构,证明不作要求);
)的共轭空间(泛函的表示形式,等距同构,证明不作要求);
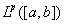 空间(
空间(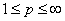 )的共轭空间(泛函的表示形式,等距同构,证明不作要求);
)的共轭空间(泛函的表示形式,等距同构,证明不作要求);
(3)泛函列的收敛: 设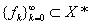 ,
,
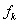 按算子范数收敛于
按算子范数收敛于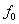 (称为强收敛):
(称为强收敛): 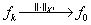 ;
;
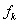 弱收敛于
弱收敛于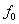 : 对于每一个
: 对于每一个 :
:  ;
;
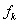 弱*收敛于
弱*收敛于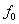 : 对于每一个
: 对于每一个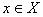 :
:  。
。
注. 1. 当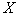 是自反空间时,弱收敛与弱*收敛等价。
是自反空间时,弱收敛与弱*收敛等价。
2. 对于泛函列的弱收敛,也有相应的Banach-Steinhaus定理。
(4)点列的收敛:
u 在赋范线性空间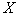 中,设
中,设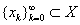 ,
,
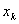 按范数收敛于
按范数收敛于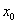 (称为强收敛):
(称为强收敛): 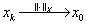 ;
;
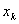 弱收敛于
弱收敛于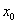 : 对于每一个
: 对于每一个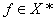 :
:  ;
;
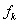 弱*收敛于
弱*收敛于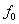 : 对于每一个
: 对于每一个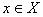 :
:  。
。
u 在Hilbert空间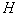 中,设
中,设 ,
,
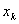 按范数收敛于
按范数收敛于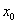 (也称为强收敛):
(也称为强收敛): 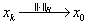 ;
;
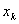 弱收敛于
弱收敛于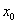 等价于 对于每一个
等价于 对于每一个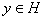 ,
,
(请参考Frechet-Riesz表示定理(P107定理3)未学,不要求)。
(4) !泛函延拓定理及其推论
注. 泛函延拓定理及其推论是重点内容,但体现在定理的应用上。
(5)*弱列紧性
Alaoglu定理(P74)、Eberlein定理(P74定理9:自反空间的单位球是弱列紧的)
请注意:
“!”表示是本课程所考察的重点内容,须引起特别注意!
“*”表示不是本课程的重点内容或必考内容.
-
泛函分析课程总结论文
湛江师范学院数科院09数本7班黎耀泽20xx29432538泛函分析课程总结论文第一部分知识点体系第七章度量空间和赋范线性空间度量…
-
泛函分析课程总结
泛函分析课程总结数学与计算科学学院09数本5班符翠艳20xx224524序号26一知识总结第七章度量空间和赋范线性空间1度量空间的…
-
泛函分析总结
泛函分析知识点小结及应用1度量空间的进一步例子设X是任一非空集合若对于xy且满足1非负性dX都有唯一确定的实数dxy与之对应xy0…
-
泛函分析总结
泛函分析知识点小结及应用第七章度量空间1度量空间的进一步例子一度量空间的定义设X是任一非空集合若对于xyX都有唯一确定的实数dxy…
-
泛函分析知识总结
泛函分析知识总结与举例应用学习泛函分析主要学习了五大主要内容一度量空间和赋范线性空间二有界线性算子和连续线性泛函三内积空间和希尔伯…
-
泛函分析课程总结论文
湛江师范学院数科院09数本7班黎耀泽20xx29432538泛函分析课程总结论文第一部分知识点体系第七章度量空间和赋范线性空间度量…
-
泛函分析课程总结
泛函分析课程总结数学与计算科学学院09数本5班符翠艳20xx224524序号26一知识总结第七章度量空间和赋范线性空间1度量空间的…
-
泛函分析总结
泛函分析知识点小结及应用第七章度量空间1度量空间的进一步例子一度量空间的定义设X是任一非空集合若对于xyX都有唯一确定的实数dxy…
-
泛函分析知识总结
泛函分析知识总结与举例应用学习泛函分析主要学习了五大主要内容一度量空间和赋范线性空间二有界线性算子和连续线性泛函三内积空间和希尔伯…
-
泛函分析概念总结
泛函分析课程论文泛函分析课程的知识体系总结各个知识点之间的区别和联系一度量空间和赋范线性空间第一节度量空间的进一步例子1距离空间的…