期末复习计划

年级：四年级                                  学 科：语文

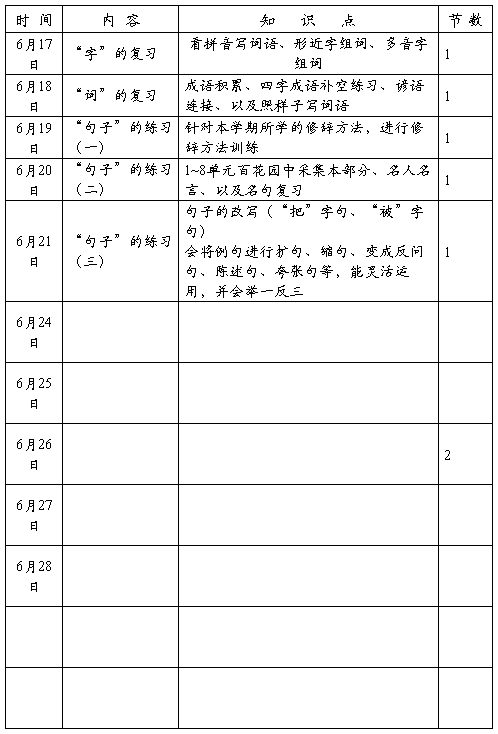
 四年级语文学科“字”的复习  (单元)期末复习检测

 

第二篇：排列组合期末复习

高二期末复习学案—排列、组合和二项式定理

【课前导学】

【学习目标】 1.掌握分类计数原理与分步计数原理，并能用它们分析和解决一些简单的应用问题.

2.理解排列与组合的意义，掌握排列数与组合数的计算公式，掌握组合数的两个性质，并能用它们解决一些简单的应用问题.

3.掌握二项式定理和二项展开式的性质，并能用它们计算和证明一些简单的问题.

【回顾旧知，理清思路】

1．两个基本原理

（1）分类计数原理中的分类；

（2）分步计数原理中的分步；

2．排列

（1）排列定义，排列数

（2）排列数公式Anm =n?(n－1)...(n－m+1)；

（3）全排列列： =n!；

（4）记住下列几个阶乘数：

0！= ，1！= ，2！= ，3！= ，4！= ，5！= ，6！= ；

3．组合

（1）组合的定义，排列与组合的区别；

（2）组合数公式Cnm= = ；

（3）组合数的性质

① ；②

4．二项式定理

（1）二项式展开公式： ；

（2）通项公式：二项式展开式中第k+1项的通项公式是： ；

（3）

5．二项式的应用

（1）求某些多项式系数的和；

（2）证明一些简单的组合恒等式；

（3）证明整除性。①求数的末位；②数的整除性及求系数； （4）近似计算。当|x|充分小时，我们常用下列公式估计近似值：

①(1+x)n≈1+nx；②(1+x)n≈1+nx+x2；

[自我检测，发现问题]

1. 有三个不同的信箱，今有四封不同的信欲投其中，则不同的投法有 种。

A．81 B．64 C．24 D．4

2. 从4名男生和3名女生中选出3人，分别从事三项不同的工作，若这3人中至少有1名女生，则选派方案共有（ ）

A 108种 B 186种 C 216种 D 270种

3．在数字1,2，3与符号＋，－五个元素的所有全排列中，任意两个数字都不相邻的全排列个数是（ ）

A 6 B 12 C 18 D 24

4．高三（一）班学要安排毕业晚会的4各音乐节目，2个舞蹈节目和1个曲艺节目的演出顺序，要求两个舞蹈节目不连排，则不同排法的种数是（ ）

A 1800 B 3600 C 4320 D 5040

5.二项式(a+b)2n展开式的项数是（ ）

A 2n B 2n+1 C 2n-1 D 2(n+1)

6.在 的展开式中， 的系数是

7. 化简 =

【自我感悟，整理问题】

【课堂导学】

思考一：组合问题的解决方案

【例1】 从集合{1，2，3，...，10}中，选出由5个数组成的子集，使得这5个数中的任何两个数的和不等于11，这样的子集共有多少个?

【例2】以三棱柱的顶点为顶点共可组成多少个不同的三棱锥？请你分析下面的解法是否正确？说明理由

解：按照上底面取出点的个数分三类：第一类，上底面恰取一点，这时下底面取三点，有 ＝3个；第二类，上底面恰取2点，下底面也取两点，有＝9个；上底面取3点时，下底面取一点，有 ＝3个.综上知，共可组成3＋9＋3＝15个不同的三棱锥.

【归纳提升】

思考二：排列与组合问题的解题策略

【例3】 4名男生和3名女生并坐一排，分别回答下列问题：

（1）男生必须排在一起的坐法有多少种？

（2）女生互不相邻的坐法有多少种？

（3）男生相邻、女生也相邻的坐法有多少种？

（4）男女生相间的坐法有多少种？

（5）女生顺序已定的坐法有多少种？

【归纳提升】

思考三：应用二项式定理解决相关系数、特殊项问题

【例4】

（1）写出展开式的通项

（2）若n=7,求展开式中第四项的二项式系数及系数，及展开式中最大的二项式系数与最大的系数（★）

（3）若展开式中第5项的系数与第3项的系数之比为56:3，求n及展开式中的常数项

（4）若展开式中所有的系数之和为243，求n

【提高应用】

在（1-x）（1+x）3展开式中求x2项的系数

【归纳提升】

思考四：利用二项式定理解决整除性问题

【例5】求证（1） 能被7整除

(2) 求证: ，（ ）能被64整除

【归纳提升】

【总结评价】

知识：

方法： 自我评价：

【检测反馈】

1.从长度分别为1、2、3、4的四条线段中，任取三条的不同取法共有n种.在这些取法中，以取出的三条线段为边可组成的三角形的个数为m，则mn等于( )

A 0 B 1 C 2 D 4

2.某班新年联欢会原定的6个节目已排成节目单，开演前又增加了3个新节目，如果将这3个节目插入节目单中，那么不同的插法种数为

A 504 B 210 C 336 D 120

3.从1到10的正整数中，任意抽取两个相加，所得和为奇数的不同情形有__________种.

4.4棵柳树和4棵杨树栽成一行，柳树、杨树逐一相间的栽法有__________种

5. 求 展开式中含 的项

6.已知 ，

1） = ， =

2） =

3） =

【例1】 解：和为11的数共有5组：1与10，2与9，3与8，4与7，5与6，子集中的元素不能取自同一组中的两数，即子集中的元素取自5个组中的一个数.而每个数的取法有2种，

所以子集的个数为2×2×2×2×2=25=32.

评述：解本题的关键是找出和为11的5组数，然后再用分步计数原理求解.

深化拓展

上例中选出5个数组成子集改为选出4个数呢?

答案：C?24=80个.

【例3】错因: 在上述解法中，第二类情形时，所取四点有可能共面.这时，务必注意在上底面取2点，与之对应的下底面的2点只有2种取法.

正解：在三棱柱的六个顶点中任取4个顶点有＝15取法，其中侧面上的四点不能构成三棱锥，故有15－3＝12个不同的三棱锥.

【例4】解：⑴从整体出发，视四名男生为一整体，看成一个"大元素"，与三名女生共四个元素进行排列，有种坐法；而大元素内部的小元素间又有种坐法.故共有＝576种坐法.

⑵因为女生 互不相邻，故先将4名男生排好，有种排法；然后在男生之间及其首尾的

5个空档中插入3名女生，有种排法.故共有＝1440种排法.

⑶类似（1）可得：＝288种

⑷男生排好后，要保证男生互不相邻、女生也互不相邻，3名女生只能排在男生之间的3个空档中，有种排法.故共有＝144种排法.

⑸7个元素的全排列有种，因为女生定序，而她们的顺序不固定时有排法，可知 中重复了次，故共有÷＝＝840种排法.

本题还可这样考虑：让男生先占7个位置中的4个，共有种排法；余下的位置排女生，因为女生定序，故她们只有1排法，从而共有＝840种排法.

●闯关训练

夯实基础

A.0 B. C. D.

解析：n=C=4，在"1、2、3、4"这四条线段中，由三角形的性质"两边之和大于第三边，两边之差小于第三边"知可组成三角形的有"2、3、4"，m=1.∴= .

答案：B

解析：三个新节目一个一个插入节目单中，分别有7、8、9种方法. ∴插法种数为7×8×9=504或A÷A=504. 答案：A

解析：当且仅当偶数加上奇数后和为奇数，从而不同情形有5×5=25种.

答案：25

4.从图中的12个点中任取3个点作为一组，其中可构成三角形的组数是 A.208

B.204 C.200 D.196

解析：在12个点中任取3个点的组合数为C，在同一直线上的3点的组数为20，则可构成三角形的组数为C－20=200.

答案：C

5.4棵柳树和4棵杨树栽成一行，柳树、杨树逐一相间的栽法有_____________种. 解析：2A?A=1152种.

答案：1152

6.某餐厅供应客饭，每位顾客可以在餐厅提供的菜肴中任选2菜2素共4种不同的品种.现在餐厅准备了5种不同的荤菜，若要保证每位顾客有200种以上的不同选择，则餐厅至少还需要不同的素菜品种_____________种.（结果用数值表示）

解析：设素菜n种，则C?C≥200n（n－1）≥40，所以n的最小值为7.

答案：7

培养能力

7.如图，一个地区分为5个行政区域，现给地图着色，要求相邻区域不得使用同一颜色.现有4种颜色可供选择，则不同的着色方法共有_____________种（以数字作答）. 解析：依次染①、②、③、④、⑤.故有C?C?C?C?C=72种.

答案：72

8.（理）设有编号为1，2，3，4，5的五个球和编号为1，2，3，4，5的五个盒子.现将这五个球投放入这五个盒子内，要求每个盒子内投放一球，并且恰好有两个球的编号与盒子的编号相同，则这样的投放方法有多少种?

分析：五个球分别投放到五个盒子内，恰好有两个球的编号与盒子的编号相同，则其他

三个球必不能投放到与球的编号相同的盒子内，此时，这三个球与对应的三个盒子，就成了受限的特殊元素与特殊位置.

解：先在五个球中任选两个球投放到与球编号相同的盒子内，有C种；剩下的三个球，不失一般性，不妨设编号为3，4，5，投放3号球的方法数为C，则投放4，5号球的方法只有一种，根据分步计数原理共有C?C=20种.

评述：本题投放球有两种方法，一种是投入到与编号相同的盒子内，另一种是投入到与编号不同的盒子内，故应分步完成.

（文）在所有两位数中，个位数字大于十位数字的两位数共有多少个?

分析：在0~9这10个数字中，按照题目要求组成的两位数中，个位数字不能为0和1，十位数字不能为0和9.也就是说组成两位数的数字可按个位分类或按十位分类来计算.

解法一：按个位数字是2，3，4，5，6，7，8，9分成8类，在每一类中满足条件的两位数分别是1个，2个，3个，4个，5个，6个，7个，8个.

则共有1+2+3+4+...+7+8=36（个）.

解法二：按十位数字是1，2，3，4，5，6，7，8分成8类，在每一类中满足条件的两位数分别是8个，7个，6个，5个，4个，3个，2个，1个.

则共有8+7+6+5+4+3+2+1=36（个）.

评述：在具体分类或分步时，常遇到困难，要多练习，多积累经验，掌握思维方法，逐步做到恰当分类，合理分步.

9.五名学生报名参加四项体育比赛，每人限报一项，报名方法的种数为多少？又他们争夺这四项比赛的冠军，获得冠军的可能性有多少种？

解：（1）5名学生中任一名均可报其中的任一项，因此每个学生都有4种报名方法，5名学生都报了项目才能算完成这一事件.故报名方法种数为4×4×4×4×4=45种.

（2）每个项目只有一个冠军，每一名学生都可能获得其中的一项获军，因此每个项目获冠军的可能性有5种.故有n=5×５×５×５=54种.

探究创新

10.三边长均为整数，且最大边长为11的三角形的个数是多少?

解：设较小的两边长为x、y且x≤y，

则 x≤y≤11，

x+y>11，

x、y∈N*.

当x=1时，y=11；

当x=2时，y=10，11；

当x=3时，y=9，10，11；

当x=4时，y=8，9，10，11；

当x=5时，y=7，8，9，10，11；

当x=6时，y=6，7，8，9，10，11；

当x=7时，y=7，8，9，10，11；

......

当x=11时，y=11.

所以不同三角形的个数为

1+2+3+4+5+6+5+4+3+2+1=36.

评述：本题关键是列出约束条件，然后寻找x=1，2，...，11时，y的取值个数的规律，再用分类计数原理求解.