广东高考-数列题型总结及练习
复习资料---数列题型总结及练习
考点一:等差、等比数列的概念与性质
<一> 等差、等比数列的证明、判断、求
例1.等差数列 中,已知
中,已知 ,试求n的值
,试求n的值
<二> 利用等差、等比的性质,求
例2、在等比数列 的前n项和中,
的前n项和中, 最小,且
最小,且 ,前n项和
,前n项和 ,求n和公比q
,求n和公比q
考点二:求数列的通项与求和
<一>、含有 的递推数列,公式
的递推数列,公式
例3.已知下面各数列 的前
的前 项和公式,求
项和公式,求 的通项公式,
的通项公式,
(1) ,求
,求 的通项公式,
的通项公式,
例4. (2008深圳模拟)已知数列
(1)求数列 的通项公式; (2)求数列
的通项公式; (2)求数列
<二> 1、形如 的递推数列,用累加法求
的递推数列,用累加法求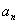
例5、(1)已知数列 中,
中, ,求数列的通项公式
,求数列的通项公式
(2)已知数列 中,
中, ,求数列的通项公式
,求数列的通项公式
(3)已知数列 中,
中, ,求数列的通项公式
,求数列的通项公式
2、形如 的递推数列,用累乘法
的递推数列,用累乘法
例6、已知数列 中,
中, ,求数列的通项公式
,求数列的通项公式
3、 形如 的递推数列,需构造新数列为等比数列
的递推数列,需构造新数列为等比数列
例7、已知数列 中,
中, ,求数列的通项公式
,求数列的通项公式
附加:形如函数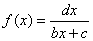 的递推数列,等式两边取倒数构造新数列为等差或等比
的递推数列,等式两边取倒数构造新数列为等差或等比
附加例、已知数列 中,
中, ,
,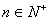 ,求数列的通项公式
,求数列的通项公式
<三>1、错位相加法求
例8、已知等差数列 的前n项和为
的前n项和为 ,且
,且 ,
, . 数列
. 数列 是等比数列,
是等比数列, (其中
(其中 ).(I)求数列
).(I)求数列 和
和 的通项公式;(II)记
的通项公式;(II)记 .
.
2、拆项相消法求 ,分组求和法求
,分组求和法求
例9、求和: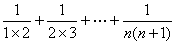
反馈练习
1、 在等差数列 中,已知
中,已知 ,则
,则 =__________.
=__________.
2、已知下面各数列 的前
的前 项和公式,求
项和公式,求 的通项公式,
的通项公式,
(1) (2)
(2)

3、已知数列{an}的前n项和满足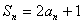 ,求此数列的通项公式.
,求此数列的通项公式.
4、在数列{an}中,an=11-2n.
⑴求Sn; ⑵设bn=|an|,求{bn}的前n项之和Tn.
5、(1)数列 中,
中, ,求数列
,求数列 的通项公式
的通项公式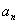
(2)已知数列 中,
中, ,求数列的通项公式
,求数列的通项公式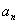
(3)已知数列 中,
中, ,求数列的通项公式
,求数列的通项公式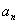
6、已知数列 中,
中, ,求数列的通项公式
,求数列的通项公式
7、(本小题满分12分)
已知数列 的前n项和为Sn,且对任意正整数n都有
的前n项和为Sn,且对任意正整数n都有 求数列
求数列 的通项公式;
的通项公式;
8、(1)已知数列 中,
中, ,求数列的通项公式
,求数列的通项公式
(2)已知数列 中,
中, ,求数列的通项公式
,求数列的通项公式
9、已知数列 中,
中, ,
,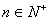 ,求数列的通项公式
,求数列的通项公式
10、求和: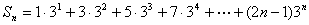
11、设数列 的前n项和为Sn=2n2,
的前n项和为Sn=2n2, 为等比数列,且
为等比数列,且
(Ⅰ)求数列 和
和 的通项公式;
的通项公式;
(Ⅱ)设 ,求数列
,求数列 的前n项和Tn.
的前n项和Tn.
12、数列 的通项公式是
的通项公式是 ,若前
,若前 项和为
项和为 ,求项数
,求项数
13、求和: ?
?
14.设 ,求
,求 的值
的值
第二篇:高中数列题型总结
关于数列求通项的方法
类型1:形如 (即:已知前n项和Sn 求
(即:已知前n项和Sn 求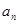 )
)
方法: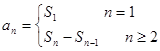 (注意:不能忘记讨论
(注意:不能忘记讨论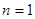 !)
!)
1.已知数列 的前n项的和
的前n项的和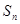 满足
满足 ,则
,则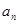 = .
= .
类型2:形如 (即:已知前n项积Tn 求
(即:已知前n项积Tn 求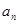 )
)
方法:一般可求Tn-1,则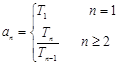 。【留尾法】
。【留尾法】
2.数列 中,
中,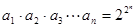 ,则此数列的通项公式为
,则此数列的通项公式为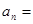 __________
__________
3.数列{an}满足a1+ 3·a2+ 32·a3+…+ 3n-1·an= ,则an=
,则an=
A  B
B 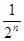 C
C  D
D 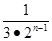
类型3:形如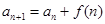 (即:后项减去前项得一变量)
(即:后项减去前项得一变量)
解法:把原递推公式转化为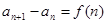 ,利用累加法求解。
,利用累加法求解。
4.已知数列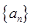 满足
满足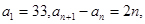 则
则 的最小值为___ _______.
的最小值为___ _______.
5.在数列{an}中,a1=2,an+1=an+ln(1+),则an= ( )
A.2+lnn B.2+(n-1)lnn C.2+nlnn D.1+n+lnn
类型4:形如 (即:后项除以前项得一变量)
(即:后项除以前项得一变量)
解法:把原递推公式转化为 ,利用累乘法求解。
,利用累乘法求解。
6.在数列 中,
中, ,
,  , 则
, 则 通项公式
通项公式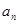 =
=
类型5:形如
 ,
,
方法:取倒数变成 的形式的方法叫倒数变换.
的形式的方法叫倒数变换.
7.已知数列 的首项
的首项 ,
, ,
, ….求数列
….求数列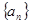 的通项公式
的通项公式
类型6:待定系数法
情况1:用于 型已知条件。转化方法:设
型已知条件。转化方法:设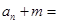
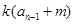 ,由km-m=b求出m的值,则数列
,由km-m=b求出m的值,则数列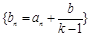 是以
是以 为公比的等比数列;通过求出
为公比的等比数列;通过求出 间接求出通项
间接求出通项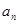 .
.
8.数列{an}中,若a1=1,an+1=2an+3 (n≥1),则该数列的通项an= .
情况2:用于 型已知条件。
型已知条件。
转化步骤:(1)等式两边同时除以 :
: ;(2)令
;(2)令 ,则
,则 ;当
;当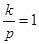 时,
时, 是以1为公差的等差数列;当
是以1为公差的等差数列;当 时,转化为类型一构造等比数列;
时,转化为类型一构造等比数列;
9.数列 中,
中,  ,
, ,则此数列的通项公式为
,则此数列的通项公式为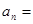 ______
______
类型8:周期数列
10.已知 ,则
,则 ( )
( )
A  B
B  C
C  D
D 
类型9:形如
方法:进退相减法(替换法)
11.设数列 的前
的前 项和为
项和为 已知
已知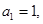

(I)设 ,证明数列
,证明数列 是等比数列 (II)求数列
是等比数列 (II)求数列 的通项公式。
的通项公式。
关于数列求和的方法
类型1: 分组求和:有一类数列,既不是等差数列,也不是等比数列,若将这类数列适当拆开,可分为几个等差、等比或常见的数列,然后分别求和,再将其合并即可.
1 已知等差数列{an}的前n项和为Sn,且a3=5,S15=225。
(1)求数列{an}的通项an;
(2)设bn= +2n,求数列{bn}的前n项和Tn。
+2n,求数列{bn}的前n项和Tn。
类型2: 并项求和:针对一些特殊的数列(主要是摆动数列),将某些项合并在一起就具有某种特殊的性质,因此,在求数列的和时,可将这些项放在一起先求和,然后再求Sn(注:多数情况下是需要对n的奇偶性进行分类讨论!)
2.已知数列{an}的前n项和为 则
则 的值为 ( )
的值为 ( )
A 13 B-76 C46 D 76
类型3:裂项相消法:这是分解与组合思想在数列求和中的具体应用. 裂项法的实质是将数列中的每项(通项)分解,然后重新组合,使之能消去一些项,最终达到求和的目的.
常见的裂项:
(1) (2)
(2)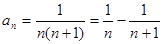
3.已知数列{an}的通项公式an=,若它的前n项和为10,则项数n为________.
4. 已知等差数列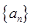 满足:
满足: ,
, ,
,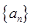 的前n项和为
的前n项和为 .
.
(Ⅰ)求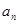 及
及 ;
;
(Ⅱ)令bn=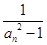 (n
(n N*),求数列
N*),求数列 的前n项和
的前n项和 .
.
类型4错位相减法:形如 或
或 (其中
(其中 为等差数列;
为等差数列; 为等比数列)
为等比数列)
5.已知数列{an}的前n项和为Sn,Sn=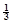 (an-1)(nÎN,n³1)
(an-1)(nÎN,n³1)
(1)求a1,a2
(2)求数列{an}的通项公式
(3)bn=n,令Cn=bnan ,求数列{Cn}的前n项和
类型5倒序相加法:这是推导等差数列的前n项和公式时所用的方法,就是将一个数列倒过来排列(反序),再把它与原数列相加,就可以得到n个 .
.
6. .
.
-
高考数列常考题型归纳总结
高考数列常考题型归纳总结类型1an1anfn解法把原递推公式转化为an1anfn利用累加法逐差相加法求解例已知数列an满足a1解由…
-
高考数列题型归纳及例题分析
数列一选择题3广东省深圳市20xx年3月高三第一次调研理科已知Sn为等差数列an的前n项和若S11的值为ASS44则6S2S493…
-
数列题型总结
题型1已知数列前几项求通项公式01数列的通项an2数列n为奇数n为偶数11111n的通项an112233445nn11357n12…
-
高中数学复习系列---数列常见题型总结
高中数学复习系列---数列(常见、常考题型总结)题型一:求值类的计算题(多关于等差等比数列)A)根据基本量求解(方程的思想)1、已…
-
高考递推数列题型分类归纳解析
wwwzgjhjycom授课教案学员姓名授课教师所授科目学员年级上课时间年月日时分至时分共小时wwwzgjhjycomwwwzgj…
-
高中数学等差数列题型总结
一、等差数列1、数列的概念例1.根据数列前4项,写出它的通项公式:(1)1,3,5,7??;(2)2?122,3?132,4?14…