一，算法程序

#include <iostream>

using namespace std; /*圆盘的个数最多为64*/

const int MAX = 64; /*用来表示每根柱子的信息*/

struct st{

int s[MAX]; /*柱子上的圆盘存储情况*/

int top; /*栈顶，用来最上面的圆盘*/

char name; /*柱子的名字，可以是A，B，C中的一个*/

int Top() /*取栈顶元素*/

{

return s[top];

}

int Pop()

{

return s[top--];

}

void Push(int x)

{

s[++top] = x;

}

} ;

long Pow(int x, int y); /*计算x^y */

void Creat(st ta[], int n); /*给结构数组设置初值*/

void Hannuota(st ta[], long max); /*移动汉诺塔的主要函数 */

int main(void)

{

int n;

cin >> n; /*输入圆盘的个数*/

st ta[3]; /*三根柱子的信息用结构数组存储*/

Creat(ta, n); /*给结构数组设置初值*/

long max = Pow(2, n) - 1; /*动的次数应等于2^n – 1*/

Hannuota(ta, max); /*移动汉诺塔的主要函数*/

system("pause");

return 0;

}

void Creat(st ta[], int n)

{

ta[0].name = 'A';

ta[0].top = n-1; /*把所有的圆盘按从大到小的顺序放在柱子A上*/ for (int i=0; i<n; i++)

ta[0].s[i] = n - i; /*柱子B，C上开始没有没有圆盘*/ ta[1].top = ta[2].top = 0;

for ( i=0; i<n; i++)

ta[1].s[i] = ta[2].s[i] = 0; /*若n为偶数，按顺时针方向依次摆放 A

B C*/

if (n%2 == 0)

{

ta[1].name = 'B';

ta[2].name = 'C';

}

else /*若n为奇数，按顺时针方向依次摆放 A C B*/

{

ta[1].name = 'C';

ta[2].name = 'B';

}

}

long Pow(int x, int y)

{

long sum = 1;

for (int i=0; i<y; i++)

sum *= x;

return sum;

}

void Hannuota(st ta[], long max)

{

int k = 0;

int i = 0;

int ch;

while (k < max)

{

/*按顺时针方向把圆盘1从现在的柱子移动到下一根柱子*/

ch = ta[i%3].Pop();

ta[(i+1)%3].Push(ch);

cout << ++k << ": " <<

"Move disk " << ch << " from " << ta[i%3].name <<

" to " << ta[(i+1)%3].name << endl;

i++;

/*把另外两根柱子上可以移动的圆盘移动到新的柱子上*/

if (k < max)

{ /*把非空柱子上的圆盘移动到空柱子上，当两根柱子都为空时，移动较小的圆盘*/

if (ta[(i+1)%3].Top()==0 || ta[(i-1)%3].Top()>0 && ta[(i+1)%3].Top() >ta[(i-1)%3].Top())

{

ch = ta[(i-1)%3].Pop();

ta[(i+1)%3].Push(ch);

cout << ++k << ": " << "Move disk " << ch << " from " <<

ta[(i-1)%3].name << " to " << ta[(i+1)%3].name << endl;

}

else

{

ch = ta[(i+1)%3].Pop();

ta[(i-1)%3].Push(ch);

cout << ++k << ": " << "Move disk "

<< ch << " from " << ta[(i+1)%3].name

<< " to " << ta[(i-1)%3].name << endl;

}

}

}

}

二,实验感想

在实际操作过程中犯的一些错误还会有意外的收获，感觉很有意思。在具体操作中对这学期所学的数据结构的理论知识得到巩固，达到设计的基本目的，也发现自己的不足之处，在以后的上机中应更加注意。

通过对汉诺塔算法的分析让我更清楚的认识到了不同的算法对程序性能的影响，也让我明白掌握了算法将会有助于提高软件的开发。

 

第二篇：分治法之汉诺塔实验报告

陕西师范大学实验报告

课题名称 算法分析与设计

项目名称 分治法  汉诺塔问题

学    院 计算机科学学院

专    业 计算机科学与技术

指导老师    王小明  

  小组人员  刘永军高富雷武子超 

        

报告时间  2013/11/28  

                                   2013/11/28

分治法之汉诺塔问题

目录

一、       设计目的... 3

二、       设计内容... 3

1．     任务描述... 3

i.     汉诺塔问题简介... 3

ii.    设计任务简介... 3

2．     分治法算法的实现过程... 4

三、       流程图... 6

四、       测试结果... 7

五、       总结... 7

附：程序源代码... 7

一、   设计目的

1、掌握分治法的思想；

2、掌握分治法的典型问题，如汉诺塔问题以及其他问题；

3、进一步多级调度的基本思想和算法设计方法；

4、提高分析与解决问题的能力。

二、            设计内容

1．     任务描述

                       i.              汉诺塔问题简介

在世界中心贝拿勒斯（在印度北部）的圣庙里，一块黄铜板上插着三根宝石针。印度教的主神大梵天在创造世界的时候，在其中一根针上从下到上地穿好了由大到小的64片金片，这就是所谓的汉诺塔。不论白天黑夜，总有一个僧侣在按照下面的法则移动这些金片：一次只移动一片，不管在哪根针上，小片必须在大片上面。僧侣们预言，当所有的金片都从大梵天穿好的那根针上移到另外一根针上时，世界就将在一声霹雳中消灭，而梵塔、庙宇和众生也都将同归于尽。

             ii.          设计任务简介

其实算法非常简单，当盘子的个数为n时，移动的次数应等于2^n - 1（有兴趣的可以自己证明试试看）。后来一位美国学者发现一种出人意料的简单方法，只要轮流进行两步操作就可以了。首先把三根柱子按顺序排成品字型，把所有的圆盘按从大到小的顺序放在柱子A上，根据圆盘的数量确定柱子的排放顺序：若n为偶数，按顺时针方向依次摆放 A B C；
若n为奇数，按顺时针方向依次摆放 A C B。
（1）按顺时针方向把圆盘1从现在的柱子移动到下一根柱子，即当n为偶数时，若圆盘1在柱子A，则把它移动到B；若圆盘1在柱子B，则把它移动到C；若圆盘1在柱子C，则把它移动到A。
（2）接着，把另外两根柱子上可以移动的圆盘移动到新的柱子上。即把非空柱子上的圆盘移动到空柱子上，当两根柱子都非空时，移动较小的圆盘。这一步没有明确规定移动哪个圆盘，你可能以为会有多种可能性，其实不然，可实施的行动是唯一的。
（3）反复进行（1）（2）操作，最后就能按规定完成汉诺塔的移动。
所以结果非常简单，就是按照移动规则向一个方向移动金片：
如3阶汉诺塔的移动：A→C,A→B,C→B,A→C,B→A,B→C,A→C。

2．     分治法算法的实现过程

首先把三根柱子按顺序排成品字型，把所有的圆盘按从大到小的顺序放在柱子A上，根据圆盘的数量确定柱子的排放顺序：

若n为偶数，按顺时针方向依次摆放 A B C；

若n为奇数，按顺时针方向依次摆放 A C B。
（1）按顺时针方向把圆盘1从现在的柱子移动到下一根柱子，即当n为偶数时，若圆盘1在柱子A，则把它移动到B；若圆盘1在柱子B，则把它移动到C；若圆盘1在柱子C，则把它移动到A。
（2）接着，把另外两根柱子上可以移动的圆盘移动到新的柱子上。即把非空柱子上的圆盘移动到空柱子上，当两根柱子都非空时，移动较小的圆盘。这一步没有明确规定移动哪个圆盘，你可能以为会有多种可能性，其实不然，可实施的行动是唯一的。
（3）反复进行（1）（2）操作，最后就能按规定完成汉诺塔的移动。
所以结果非常简单，就是按照移动规则向一个方向移动金片：

如是解决，我们就可以将n个盘分治成1个，2个，3个盘来讨论，

如1阶汉诺塔的移动： A→C；

如2阶汉诺塔的移动：A→B, A→C, B→C;
如3阶汉诺塔的移动：A→C,A→B,C→B,A→C,B→A,B→C,A→C。

通过最简单的，最少阶数汉诺塔的移动，我们更具上面的讲解，联想到更多的阶数，不难看出其中的规律！

因此，我们通过将多阶汉诺塔分解成少数像3阶一样的汉诺塔，从繁化简，分而治之。解决汉诺塔问题。

算法如下：

void move(char a,int n,char c)

{

     printf("%c-->%c\n",a,c);

}

void hanoi(int n, char a, char b, char c, int &time)

{ 

     if (n==0)   

         return;

     if (n==1)  

     { 

         move(a,1,c);

         time++;

     }

     else

     {  

         hanoi(n-1,a,c,b, time);  

         move(a,n,c);

         time++;       

         hanoi(n-1,b,a,c, time);

     }   

}

int  main()

{ 

     int n;         

     printf("请输入汉诺塔的盘数:  "); 

     scanf("%d",&n);

     int time = 0;

     printf("%d个盘的汉诺塔移动方法是\n：",n);

     hanoi(n,'a','b','c',time);

     printf("移动了%d次\n", time);

     getchar();

     getchar();

     return 0;

}

算法分析：

我们通过递归调用，主函数main()调用hanoi()函数，hanoi（）函数在调用move()函数，以及hanoi()函数对自身的调用，在hanoi()函数自身调用中参数a,b的交换，实现了品字形排列，顺序逆序的实现，从而解决问题。

通过time参数的计算，我可可以知道该函数的时间复杂度是o(2^n)。

其实我们通过数学归纳法就可以知道N阶汉诺塔需要移动的次数为2^n-1。

三、            流程图

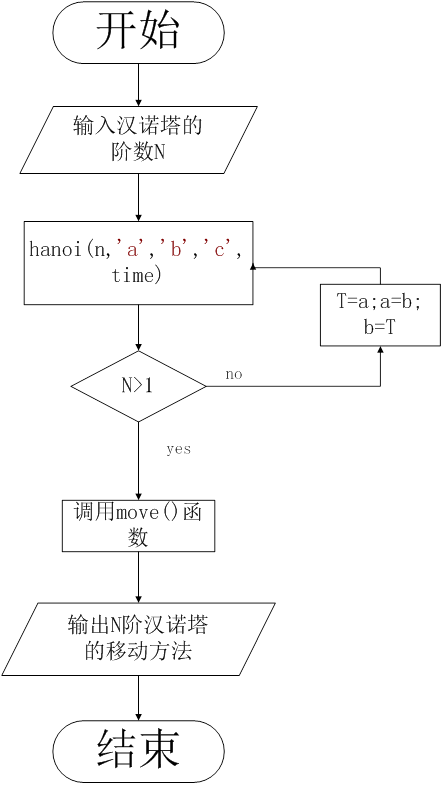
四、            测试结果

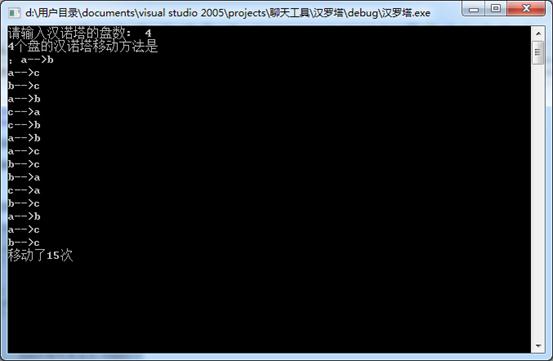
五、            总结

这次的设计的主要内容是分治算法，汉诺塔问题不难，但却是典型的分治算法中递归调用案例之一。因此通过这次练习，让我们小组更加深刻的认识到分治法的优越性以及优中求优，对算法加以修正，做到最好。

附：程序源代码

// 汉罗塔.cpp : 定义控制台应用程序的入口点。

//

#include"stdafx.h"

#include <stdio.h>

#include <stdlib.h>

void move(char a,int n,char c)

{

     printf("%c-->%c\n",a,c);

}

void hanoi(int n, char a, char b, char c, int &time)

{ 

     if (n==0)   

         return;

     if (n==1)  

     { 

         move(a,1,c);

         time++;

     }

     else

     {  

         hanoi(n-1,a,c,b, time);  

         move(a,n,c);

         time++;      

         hanoi(n-1,b,a,c, time);

     }   

}

int  main()

{ 

     int n;         

     printf("请输入汉诺塔的盘数:  "); 

     scanf("%d",&n);

     int time = 0;

     printf("%d个盘的汉诺塔移动方法是\n：",n);

     hanoi(n,'a','b','c',time);

     printf("移动了%d次\n", time);

     getchar();

     getchar();

     return 0;

}