《数值分析》报告

运用Matlab求解非线性方程的根

学    院：

专    业：

班    级：

姓    名：

学    号：

1.      目的

掌握非线性方程求根的方法，并选取实例运用MATLAB软件进行算法的实现，分别用牛顿法、弦截法和抛物线法求非线性方程的根。

2.      报告选题

报告选取《数值分析（第四版）》290页习题7作为研究对象，即求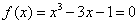在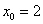附近的根。根的准确值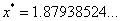，要求结果准确到四位有效数字。

（1）  用牛顿法；

（2）  用弦截法，取，；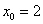

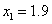（3）  用抛物线法，取，，。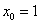

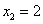3.      理论基础

(1)   牛顿迭代法

牛顿迭代法是一种特殊的不动点迭代法,其计算公式为

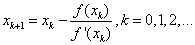
   其迭代函数为      

                

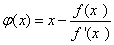
牛顿迭代法的收敛速度，当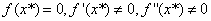时，容易证明,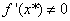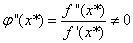，，牛顿迭代法是平方收敛的，且 。                

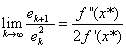（2）弦截法

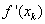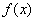将牛顿迭代法中的用在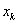，处的一阶差商来代替,即可得弦截法

          。           

（3）抛物线法

弦截法可以理解为用过两点的直线方程的根近似替的根。若已知的三个近似根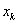，，用过的抛物线方程的根近似代替的根，所得的迭代法称为抛物线法,也称密勒(Muller)法。

4.      MATLAB实现

根据牛顿法、弦截法和抛物线法求非线性方程根的理论基础，为实现计算在MATLAB中编写了以下M文件：

（1）    f.m,题目中的函数f

function y=f(x)

y=x^3-3*x-1;

（2）    d.m,函数f的导数

     function y=d(x)

y=3*x^2-3;

（3）    newton.m，牛顿法

function newton(f,d,x0,e,max)

%f 是要求根的方程(f(x)=0);

%d 是f(x)的导数；

%x0是所给初值,位于x*附近；

%e是给定允许误差；

%max是迭代的最大次数；

%x1是newton法求得的方程的近似解；

%err是误差估计；

%k是迭代次数；

%y是f(x)值；

k=0;

 y=feval('f',x0);

fprintf('k=%.0f  x%d=%.8f                    y%d=%.6e\n',k,k,x0,k,y)

for k=1:max

    x1=x0-feval('f',x0)/feval('d',x0);

    err=abs(x1-1.87938524);

    x0=x1;

    y=feval('f',x0);

    fprintf('k=%.0f  x%d=%.8f  e%d=%.6e  y%d=%.6e\n',k,k,x0,k,err,k,y)

    if (err<e)|(y==0)|(k==max)

        break;

    end

end

（4）    xjmethod.m弦截法

function xjmethod(f,x0,x1,e,max)

%f 是要求根的方程(f(x)=0);

%x0,x1是所给初值,位于x*附近；

%e是给定允许误差；

%max是迭代的最大次数；

%x1是弦截法求得的方程的近似解；

%err是误差估计；

%k是迭代次数；

%y是f(x)值；

fprintf('k=%.0f  x%d=%.8f                    y%d=%.8e\n',0,0,x0,0,feval('f',x0))

fprintf('k=%.0f  x%d=%.8f                    y%d=%.8e\n',1,1,x1,1,feval('f',x1))

for k=2:max

    x2=x1-(feval('f',x1)*(x1-x0))/(feval('f',x1)-feval('f',x0));

    err=abs(x2-1.87938524);

    x0=x1;

    x1=x2;

    y=feval('f',x1);

    fprintf('k=%.0f  x%d=%.8f  e%d=%.6e  y%d=%.8e\n',k,k,x1,k,err,k,y)

    if (err<e)|(y==0)|(k==max)

        break;

    end

end

（5）    pwxmethod.m抛物线法

function pwxmethod(f,x0,x1,x2,e,max)

%f 是要求根的方程(f(x)=0);

%x0,x1，x2是所给初值,位于x*附近；

%e是给定允许误差；

%max是迭代的最大次数；

%x3是弦截法求得的方程的近似解；

%err是误差估计；

%k是迭代次数；

%y是f(x)值

fprintf('k=%.0f  x%d=%.8f                    y%d=%.8e\n',0,0,x0,0,feval('f',x0))

fprintf('k=%.0f  x%d=%.8f         y%d=%.8e\n',1,1,x1,1,feval('f',x1))

fprintf('k=%.0f  x%d=%.8f                    y%d=%.8e\n',2,2,x2,2,feval('f',x2))

for k=3:max

   f0=feval('f',x0);

   f1=feval('f',x1);

   f2=feval('f',x2);

   a=(f0-f2)/(x0-x2);

   b=(f1-f2)/(x1-x2);

   c=(a-b)/(x0-x1);

   w=b+c*(x2-x1);

    if w<0

        x3=x2-(2*f2/(w-sqrt(w^2-4*c*f2)));

    elseif w>0

          x3=x2-(2*f2/(w+sqrt(w^2-4*c*f2)));

    end

    err=abs(x3-1.87938524);

    x0=x1;

    x1=x2;

    x2=x3;

    y=feval('f',x2);

    fprintf('k=%.0f  x%d=%.8f  e%d=%.6e  y%d=%.8e\n',k,k,x2,k,err,k,y)

    if (err<e)|(y==0)|(k==max)

        break;

    end

end

5.      运行结果

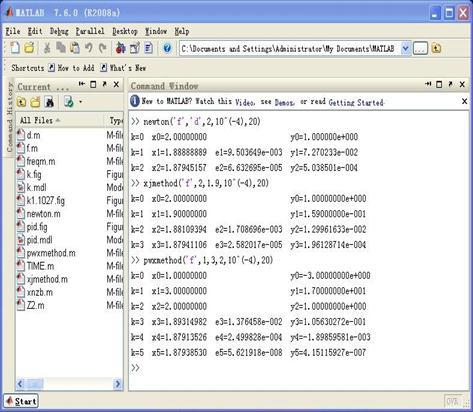
图1 运行结果界面

（1）牛顿法计算结果     

即，误差为6.632695e-005。

（2）弦截法计算结果

即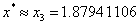，误差为2.582017e-005。

 (3) 抛物线法计算结果

即，误差为5.621918e-008。

6.      小结

迭代法是解非线性方程的主要方法，牛顿法就是最有效的迭代法之一，它在单根附近具有较高阶的收敛速度。而弦截法用差商代替导数，对于较复杂的函数运算变的方便。抛物线法也是超线性收敛的，适用于求多项式的实根和复根。

通过本次报告加深了对牛顿法、弦截法和抛物线法求解非线性方程根的理解，同时掌握了MATLAB强大的计算功能，增强了对数值分析课程的学习兴趣。

参考文献

[1] 李庆扬.数值分析（第四版）北京:清华大学出版社,施普林格出版社.2001.

[2] 胡学林.可编程控制器教程.北京:机械工业出版社,2003.

 

第二篇：数值分析：如何求解插值函数

实验报告 如何求解插值函数

题目：如何求解插值函数

摘要：在工程测量和科学实验中，所得到的数据通常都是离散的，如果要得到这些离散点意外的其他点的数值，就需要根据这些已知数据进行插值。这里我们将采用多种插值方法。

前言：（目的和意义）

掌握Lagrange,Newton,Hermite,线性，三次样条插值法的原理及应用，并能求解相应问题。

数学原理：

主要的插值法有：多项式插值法、拉格朗日插值法、线性插值法、牛顿插值法，Hermite插值法三次样条插值法等。各种插值法各有各的优点与不足。

Lagrange插值：

Hermite插值：

一次插值：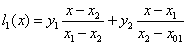

二次插值：

Newton

程序设计：

本实验采用Matlab编写。由于本实验讨论的插值函数都是一维的，故调用格式为

Y1=interp1(X,Y,X1,method)

函数根据X,Y的值，计算函数在X1处的值。

2．给出的数值表

用线性插值，二次插值及三次插值计算的近似值。

解：程序如下:

  线性插值：

  x=0.4:0.1:0.8;

  f=[-0.916291,-0.693147,-0.510826,-0.357765,-0.223144];

format long

 interp1(x,f,0.54)   

ans =

-0.620218600000000

二次插值：(采用Matlab的M文件)

x=0.54;

a=[0.4,0.5,0.6];

b=[-0.916291,-0.693147,-0.510826];

l=b(1)*(x-a(2))*(x-a(3))/((a(1)-a(2))*(a(1)-a(3)));

m=b(2)*(x-a(1))*(x-a(3))/((a(2)-a(1))*(a(2)-a(3)));

n=b(3)*(x-a(1))*(x-a(2))/((a(3)-a(1))*(a(3)-a(2)));

y=l+m+n

结果如下：

y =

      -0.61531984000000

三次样条插值：

x=0.4:0.1:0.8;

f=[-0.916291,-0.693147,-0.510826,-0.357765,-0.223144];

format long

 interp1(x,f,0.54,'spline')

ans =

-0.61597777000000

三次多项式插值：

x=0.4:0.1:0.8;

 f=[-0.916291,-0.693147,-0.510826,-0.357765,-0.223144];

format long

 interp1(x,f,0.54,'cubic')

ans =

 -0.61604826180425

2 。在上给出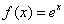的等距节点函数表，若用二次插值求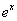的近似值，要使截断误差不超过，使用函数表的步长h应取多少？

解：若插值节点为和，则分段二次插值多项式的插值余项为

设步长为h，即

若截断误差不超过，则

那么主程序如下：

h=input('h');

if sqrt(3)/27*exp(4)*h^3<=10^(-6)

    h='yes';

else h='no';

end

h

结果是

3设，在上取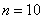，按等距节点求分段线性插值函数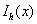，计算各节点间中点处的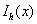与值，并估计误差。

for x=-4.5:4.5

y=1/(x^2+1)

end

=0.04705882352941；

=0.07547169811321；

=0.13793103448276；             

=0.30769230769231；

=0.80000000000000；

求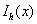的值，程序如下：

x=input('请输入x的值');

a=[x-0.5,x+0.5];

y=[1/(1+(x-0.5)^2),1/(1+(x+0.5)^2)];

I=y(1)*(x-a(2))/(a(1)-a(2))+y(2)*(x-a(1))/(a(2)-a(1))

当分别输入时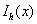，的值分别为：0.0486，0.0794,0.1500,0.3500,0.7500

20．给定数据表如下：

试求三次样条插值S(x)及Lagrange插值，并满足条件：

解：(1)

(2)

结果分析和讨论：

各种插值方法都有自己的优点。例如Lagrange插值多项式是数值积分与常微分方程数值解的重要工具，而分段多项式插值具有良好的稳定性和收敛性，更便于应用。而对同一个问题而言，用不同的插值多项式所得的解存在微小差异，故误差分析也是很必要的。