一、弹性力学的发展及基本概念、假设

弹性力学是伴随着工程问题不断发展起来的，它是固体力学的一个分支，是研究弹性体由于外力作用或温度改变等原因而发生的应力、应变和位移的一门学科。最早可以追溯到伽利略研究梁的弯曲问题、胡克的胡克定律。之后牛顿三定律的形成以及数学的不断发展，后经纳维、柯西、圣维南、艾瑞、基尔、里茨、迦辽金等人的不断努力。使得弹性力学具有了严密的理论体系并且能都求解各种复杂的问题，能够解决强度、刚度和稳定性等问题。目前弹性力学的相关理论在土木工程、水文地质工程、石油工程、航空航天工程、矿业工程、环境工程以及农业工程等诸多领域得到了广泛的应用。

弹性力学中经常用到的基本概念有外力、应变、形变和位移。作用于物体的外力可以分为体积力和表面力，两者也分别称为体力和面力。所谓体力，是分布在物体体积内的力，例如重力和惯性力。所谓面力，是分布在物体表面上的力，例如流体压力和接触力。对于应力，设作用于ΔA上的内力为ΔF，则内力的平均集度，即平均应力，为ΔF/ΔA。现在，命ΔA无限减小二趋于P点，假定内力连续分布则ΔF/ΔA将趋于极限p，这个极限矢量p就是物体在截面上的在p点的应力。如果某一个截面上的外法线是沿着坐标轴的正方向，这个截面上的应力分量就以沿坐标轴正方向时为正，沿坐标轴负方向是为负。相反，如果某一个截面上的外法线是沿着坐标轴的负方向，这个洁面霜的应力分量就以沿坐标轴负方向是为正，沿坐标轴正方向时为正。所谓形变，就是形状的改变。物体的形状总可以用它各部分的长度和角度来表示，因此，物体的形变总可以归结为长度的改变和角度的改变。所谓位移，就是位置的移动。物体内任意一点的位移，用它在x,y,z三个轴上的投影u,v,w来表示，以沿坐标轴正方向时为正，沿坐标轴负方向时为负。

下面简要介绍弹性力学的几个基本假设：

1.  假定物体是连续的，就是是假定整个物体的体积都被组成这个物体的介质所填充，不留下任何空隙。

2.      假定物体是完全弹性的，也就是假定物体完全服从胡可定律——应变与引起该应变的那个应力分量成比例；反映这种比例关系的常数，即所谓弹性常数。

3.      假定物体是均匀的，也就是整个物体是由同一材料组成的，这样整个物体的所有各部分才具有相同的弹性，因而物体的弹性常数才不随位置坐标而变，可以取出该物体的任意一小部分来加以分析，然后把分析结果应用于整个物体。

4.      假定物体是各向同行的，就是是物体内任意一点的弹性在所有各个方向是相同的。

凡是符合以上四个假定的物体，就称为理想弹性体

5.      假定位移是微小形变，这就是说假定物体受力以后，整个物体所有各点的位移都远远下雨物体的原来的尺寸，因而应变和转角都远小于1。

二．弹性力学基本方程

现在就解析法简要介绍 弹性力学的基本方程：

1．  平衡微分方程   

 

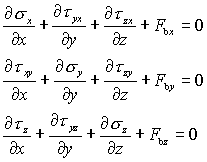
用张量形式描述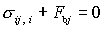

2. 几何方程   

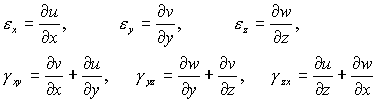
用张量形式描述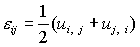        

       变形协调方程 

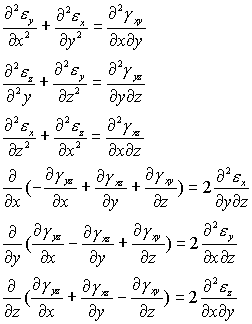
3.本构方程-广义胡克定律   

    用应力表示的本构方程

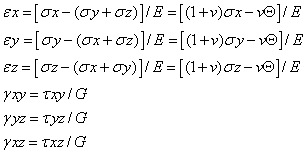
    用应变表示的本构方程 

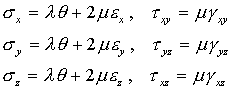
    4．边界条件：   

    如果物体表面的面力F_sx，F_sy，F_sz为已知，则边界条件应为：

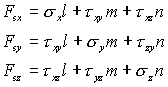
称为面力边界条件，用张量符号表示为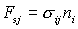

    如果物体表面的位移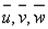已知，则边界条件应为

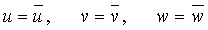
称为位移边界条件。除了面力边界条件和位移边界条件，还有混合边界条件。

    如上所述，弹性力学的基本未知量为三个位移分量，六个应力分量和六个应变分量，共计十五个未知量。基本方程为三个平衡微分方程，六个几何方程和六个物理方程，也是十五个基本方程。

 

三．弹性力学基本解题方法

   1．位移法

      为了用位移作为基本未知量，必须将泛定方程改为用位移u,v,w来表示，可以得到下列用位移表示的微分方程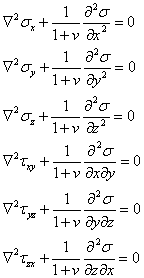 5  

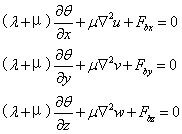
不计外力时，上式简化为其次方程

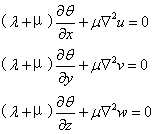
或

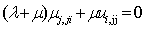
上式称为拉梅——纳斯方程。

上述方程组含有三个未知函数u,v,w。此外，边界条件也要用位移表示，当给定位移边界条件时，问题自然简单。如给定应力边界条件，则需要将边界条件加以变换，改用位移表示。由此，用位移法解弹性力学问题归结为按给定边界条件积分式。

2.应力法

     为用应力作为基本未知量，需要将泛定方程改为用应力分量表示，并求出6个应力分量所满足的6个方程。有此所求得的解，应满足应变协调条件和边界条件。为此，应将应变协调方程改为用应力表示。

可以得到下了用应力表示的6个协调方程

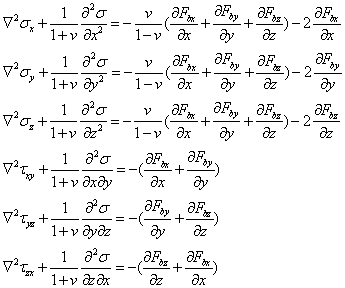
上式称为贝尔特拉米—米歇尔方程。实际上是用应力表示的协调方程，称为应力协调方程。

当外力不计时，可以简化为

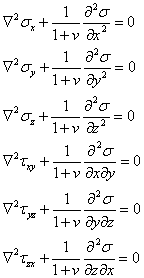
由此可知，用应力法解弹性力学问题就归结为求满足平衡方程，协调方程以及边界条件的应力分量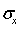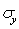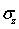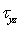，，，，，的数学问题。对于弹性力学问题需要在严格的边界条件下解复杂的微分方程组，在一般情况下这是件很不容易的事情，。因而人们研究了各种解题方法，如逆解法，半逆解法等。

所谓逆解法，就是选取一组位移或应力函数，由此求出应变与应力。然后验证是否满足基本方程。若满足，则求出与这对应的边界上的位移或面力，再与实际边界条件比较。如果相同或认可为相近，就可把所选取的解作为所要求的解。所谓半逆解法又称凑合揭发，就是在未知量中先根据问题的特点假设一部分一直，然后在基本方程和边界条件中，求另一部分。这样就得到了全部未知量。

3        复变函数法

它的基本思路时将Airy应力函数用两个解析函数表示，并将位移、应力和边界条件也表示成复变函数的形式，从而吧平面问题转化为在给定的边界条件下，去尊求两个解析函数的问题。在弹性力学问题的求解中，边界条件一般时很难完全满足的，这时我们可以利用Saint.Venant原理，使在大边界上完全满足边界条件，在小边界上等效满足。

4        有限单元法

从物理概念上看，弹性力学有限单元法是杆系结构力学的矩阵位移法（即杆系结构的有限单元法）弹性体是个连续体，为了能用结构力学的矩阵方法来计算弹性力学问题，首先必须对弹性体进行离散化，也就是将连续的弹性体分割成有限个有限大小的构件，它们通过有限个点互相联系，这些有限大小的构件就成为有限单元，简称有限元，而连接它们的点九成为结点。

通过离散化以后，由于单元之间只通过结点联系，所以物体所受到的体力和面力都应按静力等效的原则移置到结点上，成为结点载荷，这样，通过离散化就得出一个由若干单元在结点处铰接，并受已知结点载荷的结构体系，这就是有限元计算模型。

计算时通常采用位移法，即取结点的未知位移为基本未知量。对单元选择适当的位移模式即形状函数，则单元内任一点的位移可由结点位移表示，通过对单元进行变形几何关系、物理关系、静力平衡关系的分析就能得到应变、应力分量及结点对单元的作作用力，即结点力和结点位移的关系。这样，所有欲求的力学量都用结点位移表示，这一步称单元分析。

再对每一结点建立结点荷载与结点力的平衡关系，则对整个叹息可以得到一组以结点位移为未知量的代数方程，这一步称整体分析。

引入支撑条件，求解线性代数方程，求出结点位移，进而求出其它的力学量。

这就时弹性力学的有限单元法，对于这样方法，已经由许多成熟的有限元软件可以使用，如：ANSYS,NASTRAN等，它们不但可以求解平面问题，而且还可以方便的求解弹性力学的空间问题。

 

四．弹性力学例题

例1设有刚体，具有半径为 b 的圆柱形孔道，孔道内放置一外半径为 b而内半径为 a的圆筒，受内压力 q ，试求圆筒壁的应力。

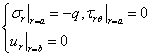
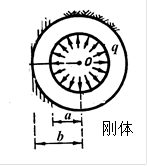解：边界条件：

 

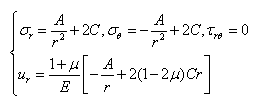
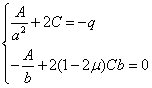代入边界条件有：

 

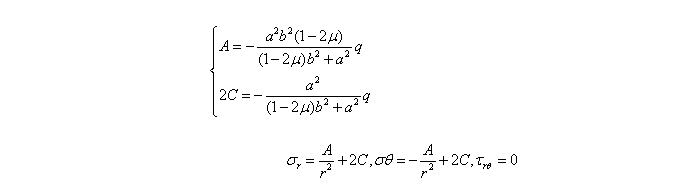
将常数A、C代入，有

 

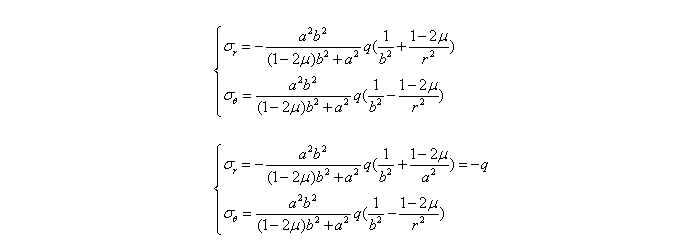
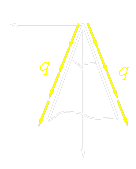
例题2. 楔形体在两侧受有均布剪应力q，如图所示。试求其应力分量。

解：（1）应力函数 j  的确定

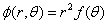由因次分析法，可知

 

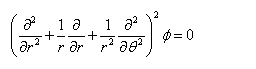
代入相容方程：

 

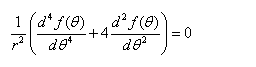
得到：

 

（2）应力分量的确定

 

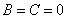
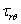
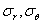由对称性，        应为q 的偶函数；   应为q 的奇函数，因而有

 

（3）由边界条件确定常数

 

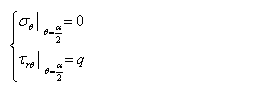
边界条件：

 

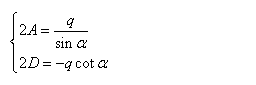
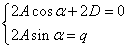代入，有：

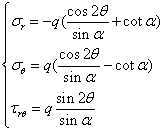代入应力分量式，有

例题3.曲梁在两端受相反的两个力P作用，如图所示。试求其应力分量。

解：（1）应力函数的确定

任取一截面  ，截面弯矩为

 

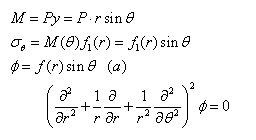
将其代入相容方程：

 

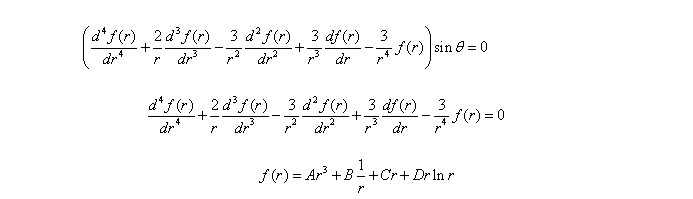
上述欧拉方程的解：                                  （b）

 

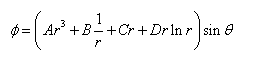
代入应力函数为                                      （c）

（2）应力分量的确定

                                              

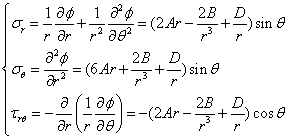
                                                   （d）

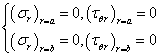边界条件：

 

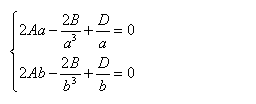
代入应力分量得：                             （e）

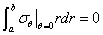
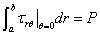
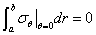端部条件（左端）：

 

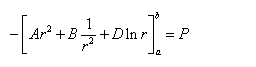
代入剪应力分量得：

 

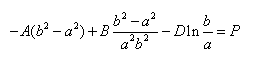
（f）

联立求解式（e）、（f），得：

 

代入应力分量式（d），有：

 

 

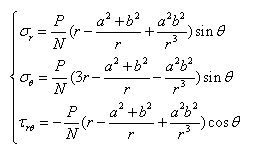
第二篇：弹性力学读书报告

《弹性力学》读书报告

弹性力学也称弹性理论，主要研究弹性体在外力作用或温度变化等外界因素下所产生的应力、应变和位移，从而解决结构或机械设计中所提出的强度和刚度问题。在研究对象上，弹性力学同材料力学和结构力学之间有一定的分工。材料力学基本上只研究杆状构件；结构力学主要是在材料力学的基础上研究杆状构件所组成的结构，即所谓杆件系统；而弹性力学研究包括杆状构件在内的各种形状的弹性体。弹性力学是固体力学的重要分支，它研究弹性物体在外力和其它外界因素作用下产生的变形和内力，也称为弹性理论。它是材料力学、结构力学、塑性力学和某些交叉学科的基础，广泛应用于建筑、机械、化工、航天等工程领域. 弹性力学问题的求解主要是基于以下几个理论基础。

1.Newton定律

弹性力学是一门力学，它服从Newton所提出的三大定律，即惯性定律﹑运动定律，以及作用与反作用定律。质点力学和刚体力学是从Newton定律演绎出来的，而弹性力学不同于理论力学，它还有新假设和新定律。

2.连续性假设

所谓连续性假设，就是认定弹性体连续分布于三维欧式空间的某个区域之内，与此相伴随的，还认定弹性体中的所有物理量都是连续的。也就是说，我们将假定密度、位移、应变、应力等物理量都是空间点的连续变量，而且也将假定空间的点变形前与

变形后应该是一一对应的。

3.广义Hooke定律

所谓广义Hooke定律，就是认为弹性体受外载后其内部所生成的应力和应变具有线性关系。对于大多数真实材料和人造材料，在一定的条件下，都符合这个实验定律。线性关系的Hooke定律是弹性力学特有的规律，是弹性力学区别于连续介质力学其他分支的标识。

Newton定律、连续性假设和广义Hooke定律，这三方面构成了弹性力学的理论基础。

弹性力学在不同的常用坐标系下有不同的基本方程。

1.直角坐标x，y，z

几何方程为

?u?v?w???,??,???x?xy?yz?z??1??v?w????yz???2?z?y??? ????1??w??u???zx2???x?z?????1??u??v?

?xy2??y?x????

平衡方程为

???x??yx??zx???fx?0??y?z??x

????xy??y??zy???fy?0 ??x?y?z??????zy??z??fz?0?xz??y?z???x

应变协调方程为

??2?yz?2?y?2?z?2?2?0?2?y??y?z?z

??2??2?z?2?xzx?2?2?0?2?z?x?x?z?

2??2??2?x??yxy?2?2?2?0?x???x?y?y

?2??yz??zx??xy???x?????????y?z?x??x?y?z?2???y????zx??xy??yz??z?x??y???y??z??x????2?????????x???xy?yz?zx??x?y???x?y?z??z???0????0????0?

Beltrami-Michell应力协调方程（无体力）为 11?22?????0,????,yx?0x,xxyz?1??1???11?22?????0,????,zx?0 ?y,yyzx1??1???11?22?????0,????,xy?0z,zzxy?1??1???

其中???x??y??z。

以位移表示的弹性力学方程为

?21???u?v?w?1?u???????fx?01?2??x??x?y?z????1???u?v?w?1?2??v??????fy?0 1?2??y?x?y?z?????1???u?v?w?1??2w??????fz?01?2??z?x?y?z?????

Papkovich-Neuber通解（无体力）为

?1?u?P??P0?xP1?yP2?zP3?1?4(1??)?x??1?v?P??P0?xP1?yP2?zP3? ?24(1??)?y??1?w?P??P0?xP1?yP2?zP3??34(1??)?z?

其中?2Pi?0(i?0,1,2,3)。

2.柱坐标r，?，z

单位矢量及其徽商

r0?icos??jsin?，?0??isin??jcos? ?r0??0?r0??0

0?0，?0，??，??r0 ?r?r????

基本关系

，x?rcos?y?rsin?，z?z ?ur?uxcos??uysin???u???uxsin??uycos? ??uz?uz

几何方程和平衡方程分别为 ??ur?uz1?u?ur??,???,???r?r?r??rz?z??11?ur?u?u???)??r??(?2r???rr ????1(?ur??uz)?rz2?z?r????1(?u??1?uz)?z?2?zr???

???r1???r??zr?r??s?fr?0??r?r????z?r?????r?1?????z?2?r?????f??0 ?r???zr??r

???1???z??z?rzrz????fz?0??rr???zr??

应变协调方程为

?2?2??z2??zr?2??1?2?z1??z??2?22??0??zr??r?r?r???zr?z

????2?z?2?rrz?2?2?0?2?r?z?r?r??2???r?1?21?1?2???(r)?(2?)?r?2(r)?0?22r?r??r??r?rr?r?r? ?2??????1?1??11???rzr???(r??z)??()?2(r2?z)?0?r???z?r?r?rr?r?z??rr???22?1?(r???)?1??r?1?(r??z?)?1??zr?1???r?0?r?r?zr?zr2?r??r2??2r???z?2??1??z?1??z?1?2?zr??r?)?r()???0?(2?rr?zr???z?z??rr??

3.球坐标r，?，?

单位矢量及其徽商

?r0?isin?cos??jsin?sin??kcos??0???icos?cos??jcos?sin??ksin?

??0??isin??jcos??

??r0

0?????

?0??r0?????sin?

????0

??r0?????0?????0cos?????0????0????0?????r0sin???0cos?????

基本关系

x?rsin?cos?，y?rsin?sin?，z?rcos? ?ur?uxsin?cos??uysin?sin??uzcos???u??uxcos?cos??uycos?sin??uzsin???u???uxsin??uycos?

几何方程为

?ur????rr????1?u??ur??r??r????1?u??cot?u?ur???rsin???rr? ?11?ur?u?u???r??(??)2r???rr??11?u?1?u?cot??????(??u?)2rsin???r??r???uu???r?1(1?ur????)?2rsin????rr?

平衡方程为

2?r?????????r1???r1???rcot??fr?0??r?r???rsin????r??r?r??1????3?r?cot????r?1???????(?????)?f??0 ?r??rsin???rr??r

???r?1????1???3?r?cot?????2????f??0??rr??rsin???rr??

应变协调方程为

?????2??1?22?22?2??r?1cot????1?1???2(?sin?)?(?sin?)???3(r??)?2?22(sin2?)???r?0?22??r?22222??r?rr2rsin???rsin???rsin???r?rr??rsin????rsin?????

?2?2?r1??rcot???r?22cot??1?2???1(r?r?)?(r?)?(r)???2?0?2r??rr2?rr2?rr2sin2???2r?rr???rsin??r??

?2?21?2?r1??r1?2????2(r?r?)?2??(r)?0?rr??2r2?rr2?r?r?r???22?2?1?(?r)?1?(r2????)?sin??(r?r?)?1(r?r?)?0?r2????sin??rr2?rr2?r??sin?r2sin??r???2??r??r?1??r1?21?cos2?1?2?1????r2?rsin??r??(sin?)?rsin????rsin??r??(???sin?)?rsin???(sin???)?rsin??r??r????(sin?)?0

?2?1?2?r??21??rcot????1????1?212(?sin?)????(?sin?)??2?r??0??r?222222rsin??r????r?rrsin??r??????rrsin?rsin???r?

弹性力学的几个例题。

例题1. 设有刚体，具有半径为 b 的圆柱形孔道，孔道内放置一外半径为 b而内半径为 a的圆筒，受内压力 q ，试求圆筒壁的应力。

解：边界条件：

?A?2C??q??a2

代入边界条件有：? ??A?2(1?2?)Cb?0??b ???rr?a??q,?r????urr?b?0r?a?0AA????2C,????2C,?r??0r?22?rr???ur?1????A?2(1?2?)Cr???E??r??刚体

22?ab(1?2?) A??q?22(1?2?)b?a? ? a2?2C??q22? (1?2?)b?a? AA将常数A、C代入，有 ?r?2?2C,????2?2C,?r??0rr 22?ab11?2? ???q(?2?r222(1?2?)b?abr? ? a2b211?2????q(?2)?222?

(1?2?)b?abr?

?a2b211?2????q(???q?r2222 (1?2?)b?aba?? a2b211?2?????q(?2) 222?(1?2?)b?abr?

例题2. 楔形体在两侧受有均布剪应力q，如图所示。试求其应力分量。

解：（1）应力函数 ? 的确定

由因次分析法，可知

??21?1?2?代入相容方程： ?2??2??02?r?rr???

??r2?(r,?)?r2f(?)

得到：

1?d4f(?)d2f(?)??4???0r2?d?4d?2?

（2）应力分量的确定

?r ? 应为? BC ?由对称性， ? r ,? ?

0 的奇? 应为? 的偶函数；??r??2Acos2??2Bsin2??2C??2D?????2Acos2??2Bsin2??2C??2D???2Asin2??2Bcos2??C?r?d4f(?)d2f(?)?4?042d?d?f(?)?Acos2??Bsin2??C??D??r2f(?)?r2(Acos2??Bsin2??C??D)

函数，因而有

??r??2Acos2??2D?????2Acos2??2D???2Asin2??r?

（3）由边界条件确定常数 ????边界条件： ???r???2???0?q???

2

?2Acos??2D?0代入，有：

? 2Asin??q?q??2A?sin????2D??

qcot?

代入应力分量式，有

cos2??

???q(?cot?)?r

sin?

?

cos2??

??q(?cot?)??

sin??

sin2????q?r?

sin??

例题3.曲梁在两端受相反的两个力P作用，如图所示。试求其应力分量。 解：（1）应力函数的确定 任取一截面 ，截面弯矩为

将其代入相容方程：

Cr上述欧拉方程的解： f (r ) ? Ar 3 ? B ? ? Dr ln r （b）

1

r

?d4f(r)2d3f(r)3d2f(r)3df(r)3?

????f(r)??sin??0432234

drrdrrdrrdrr??

M?Py?P?rsin?

???M(?)f1(r)?f1(r)sin?

ab

ry

P

??f(r)sin?(a)

??21?1?2?

?2??0?2?2?r?rr?????r

2

d4f(r)2d3f(r)3d2f(r)3df(r)3

??2?3?4f(r)?0432

drrdrrdrrdrr

Arsin? （c）代入应力函数为 ? ? ? 3 ? B ? Cr ? Dr ln r ? ? ?

?

?

1

r

（2）应力分量的确定

???r?1???1?2??(22BD?

r?rr2??2Ar?r3

?r)sin? ?????2??(6Ar?2B?D)sin? ?

??r2r3

r??

? r? ? ? ?? 1??? ? ? (2 Ar 2B ? D)cos ?

?

?r??r?????r3r边界条件： ???

??r?r?a?0,???r?r?a?0

????r?r?b?0,???r?r?b?0

?2Aa?2B?D?代入应力分量得： ??? a 3 a

?

??2Ab?2Bb3

?Db?0

端部条件（左端）：? b

a?r???0dr?P?

b

a

??

??0

dr?0

b

代入剪应力分量得： ???1?

?Ar2?Br2?Dlnr???P

a

A (b 2

? a 2

) ? B b2?a2?b

a2b2? D ln a

? P

（d）

（e）

?

b

a

??

??0

rdr?0

( f )

联立求解式（e）、（f），得：

代入应力分量式（d），有：

?Pa2?b2a2b2??r?N(r?r?r3)sin??Pa2?b2a2b2??3)sin?????(3r?Nrr??Pa2?b2a2b2?3)cos???r???(r?Nrr?PA?,2NPa2b2B??,2ND??P2(a?b2)NN?(a2?b2)?(a2?b2)lnba