高中数学选修1-2知识点归纳
推理与证明
一.推理:
⑴合情推理:归纳推理和类比推理都是根据已有事实,经过观察、分析、比较、联想,在进行归纳、类比,然后提出猜想的推理,我们把它们称为合情推理。
①归纳推理:由某类食物的部分对象具有某些特征,推出该类事物的全部对象都具有这些特征的推理,或者有个别事实概括出一般结论的推理,称为归纳推理,简称归纳。
注:归纳推理是由部分到整体,由个别到一般的推理。
②类比推理:由两类对象具有类似和其中一类对象的某些已知特征,推出另一类对象也具有这些特征的推理,称为类比推理,简称类比。
注:类比推理是特殊到特殊的推理。
⑵演绎推理:从一般的原理出发,推出某个特殊情况下的结论,这种推理叫演绎推理。
注:演绎推理是由一般到特殊的推理。
“三段论”是演绎推理的一般模式,包括:
⑴大前提---------已知的一般结论;
⑵小前提---------所研究的特殊情况;
⑶结 论---------根据一般原理,对特殊情况得出的判断。
二.证明
⒈直接证明
⑴综合法
一般地,利用已知条件和某些数学定义、定理、公理等,经过一系列的推理论证,最后推导出所要证明的结论成立,这种证明方法叫做综合法。综合法又叫顺推法或由因导果法。
⑵分析法
一般地,从要证明的结论出发,逐步寻求使它成立的充分条件,直至最后,把要证明的结论归结为判定一个明显成立的条件(已知条件、定义、定理、公理等),这种证明的方法叫分析法。分析法又叫逆推证法或执果索因法。
2.间接证明------反证法
一般地,假设原命题不成立,经过正确的推理,最后得出矛盾,因此说明假设错误,从而证明原命题成立,这种证明方法叫反证法。
复数
1.概念:
(1) z=a+bi∈R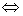 b=0 (a,b∈R)
b=0 (a,b∈R)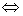 z=
z=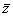
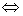 z2≥0;
z2≥0;
(2) z=a+bi是虚数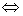 b≠0(a,b∈R);
b≠0(a,b∈R);
(3) z=a+bi是纯虚数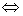 a=0且b≠0(a,b∈R)
a=0且b≠0(a,b∈R)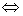 z+
z+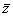 =0(z≠0)
=0(z≠0)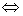 z2<0;
z2<0;
(4) a+bi=c+di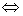 a=c且c=d(a,b,c,d∈R);
a=c且c=d(a,b,c,d∈R);
2.复数的代数形式及其运算:设z1= a + bi , z2 = c + di (a,b,c,d∈R),则:
(1) z 1±z2 = (a + b)± (c + d)i;
(2) z1.z2 = (a+bi)·(c+di)=(ac-bd)+ (ad+bc)i;
(3) z1÷z2 =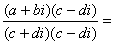
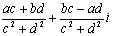 (z2≠0) ;
(z2≠0) ;
第二篇:高中数学选修1-1知识点归纳
高中数学选修1-1知识点总结
第一章 简单逻辑用语
1、命题:用语言、符号或式子表达的,可以判断真假的陈述句.
真命题:判断为真的语句.假命题:判断为假的语句.
2、“若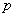 ,则
,则 ”形式的命题中的
”形式的命题中的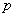 称为命题的条件,
称为命题的条件, 称为命题的结论.
称为命题的结论.
3、原命题:“若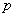 ,则
,则 ” 逆命题:“若
” 逆命题:“若 ,则
,则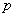 ”
”
否命题:“若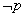 ,则
,则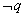 ” 逆否命题:“若
” 逆否命题:“若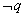 ,则
,则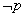 ”
”
4、四种命题的真假性之间的关系:
(1)两个命题互为逆否命题,它们有相同的真假性;
(2)两个命题为互逆命题或互否命题,它们的真假性没有关系.
5、若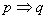 ,则
,则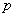 是
是 的充分条件,
的充分条件, 是
是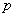 的必要条件.
的必要条件.
若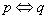 ,则
,则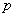 是
是 的充要条件(充分必要条件).
的充要条件(充分必要条件).
利用集合间的包含关系:例如:若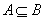 ,则A是B的充分条件或B是A的必要条件;若A=B,则A是B的充要条件;
,则A是B的充分条件或B是A的必要条件;若A=B,则A是B的充要条件;
6、逻辑联结词:⑴且(and) :命题形式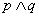 ;⑵或(or):命题形式
;⑵或(or):命题形式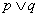 ;
;
⑶非(not):命题形式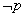 .
.

7、⑴全称量词——“所有的”、“任意一个”等,用“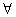 ”表示;
”表示;
全称命题p: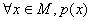 ;全称命题p的否定
;全称命题p的否定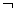 p:
p: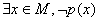 。
。
⑵存在量词——“存在一个”、“至少有一个”等,用“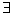 ”表示;
”表示;
特称命题p: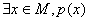 ;特称命题p的否定
;特称命题p的否定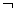 p:
p: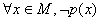 ;
;
第二章 圆锥曲线
1、平面内与两个定点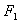 ,
,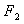 的距离之和等于常数(大于
的距离之和等于常数(大于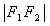 )的点的轨迹称为椭圆.
)的点的轨迹称为椭圆.
即: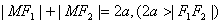 。
。
这两个定点称为椭圆的焦点,两焦点的距离称为椭圆的焦距.
2、椭圆的几何性质:
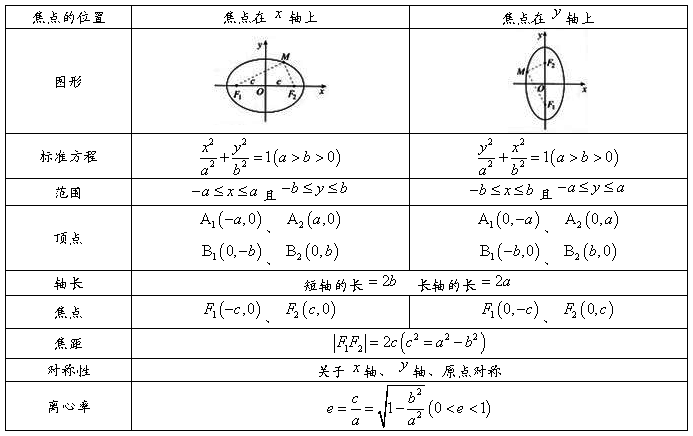
3、平面内与两个定点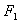 ,
,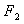 的距离之差的绝对值等于常数(小于
的距离之差的绝对值等于常数(小于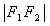 )的点的轨迹称为双曲线.即:
)的点的轨迹称为双曲线.即: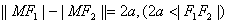 。
。
这两个定点称为双曲线的焦点,两焦点的距离称为双曲线的焦距.
4、双曲线的几何性质:
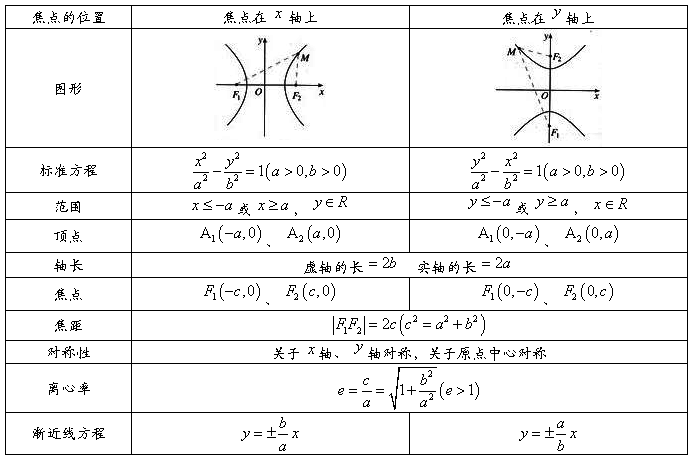
5、实轴和虚轴等长的双曲线称为等轴双曲线.
6、平面内与一个定点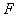 和一条定直线
和一条定直线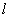 的距离相等的点的轨迹称为抛物线.定点
的距离相等的点的轨迹称为抛物线.定点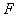 称为抛物线的焦点,定直线
称为抛物线的焦点,定直线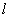 称为抛物线的准线.
称为抛物线的准线.
7、抛物线的几何性质:

8、过抛物线的焦点作垂直于对称轴且交抛物线于 、
、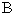 两点的线段
两点的线段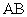 ,称为抛物线的“通径”,即
,称为抛物线的“通径”,即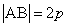 .
.
9、焦半径公式:
若点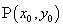 在抛物线
在抛物线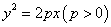 上,焦点为
上,焦点为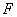 ,则
,则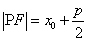 ;
;
若点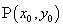 在抛物线
在抛物线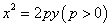 上,焦点为
上,焦点为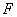 ,则
,则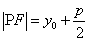 ;
;
第三章 导数及其应用
1、函数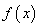 从
从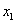 到
到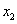 的平均变化率:
的平均变化率: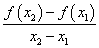
2、导数定义: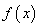 在点
在点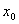 处的导数记作
处的导数记作 ;.
;.
3、函数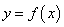 在点
在点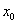 处的导数的几何意义是曲线
处的导数的几何意义是曲线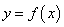 在点
在点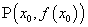 处的切线的斜率.
处的切线的斜率.
4、常见函数的导数公式:
①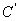
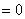 ;②
;②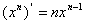 ; ③
; ③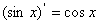 ;④
;④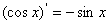 ;
;
⑤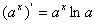 ;⑥
;⑥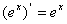 ; ⑦
; ⑦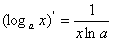 ;⑧
;⑧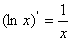
5、导数运算法则:
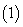
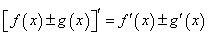 ;
;
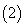
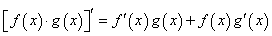 ;
;
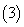
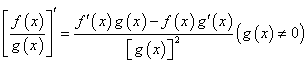 .
.
6、在某个区间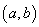 内,若
内,若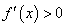 ,则函数
,则函数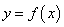 在这个区间内单调递增;
在这个区间内单调递增;
若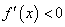 ,则函数
,则函数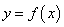 在这个区间内单调递减.
在这个区间内单调递减.
7、求函数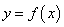 的极值的方法是:解方程
的极值的方法是:解方程 .当
.当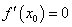 时:
时:
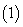 如果在
如果在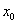 附近的左侧
附近的左侧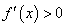 ,右侧
,右侧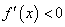 ,那么
,那么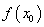 是极大值;
是极大值;
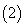 如果在
如果在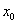 附近的左侧
附近的左侧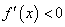 ,右侧
,右侧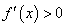 ,那么
,那么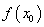 是极小值.
是极小值.
8、求函数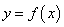 在
在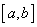 上的最大值与最小值的步骤是:
上的最大值与最小值的步骤是:
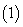 求函数
求函数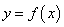 在
在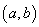 内的极值;
内的极值;
 将函数
将函数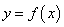 的各极值与端点处的函数值
的各极值与端点处的函数值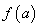 ,
,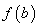 比较,其中最大的一个是最大值,最小的一个是最小值.
比较,其中最大的一个是最大值,最小的一个是最小值.
9、导数在实际问题中的应用:最优化问题。
-
高中数学选修2-1知识点总结
高二数学选修21知识点1命题用语言符号或式子表达的可以判断真假的陈述句真命题判断为真的语句假命题判断为假的语句2若p则q形式的命题…
-
高二数学(理科)选修2-1知识点总结
高二数学归纳材料实小校区TEL87530008高二数学选修21知识点归纳资料第一部分简单逻辑用语1命题用语言符号或式子表达的可以判…
-
高二数学选修2-1知识点总结
高二数学上期末复习部分知识点概要20xx15高二数学选修21知识点1命题用语言符号或式子表达的可以判断真假的陈述句真命题判断为真的…
-
高中数学选修2-2知识点总结(精华版)
数学选修22知识点总结一导数1函数的平均变化率为fx2fx1fx1xfx1yfxxx2x1x注1其中x是自变量的改变量可正可负可零…
-
高中数学选修2-1、2-2知识点小结
选修2122知识点选修21第一章常用逻辑用语1命题及其关系四种命题相互间关系逆否命题同真同假2充分条件与必要条件p是q的充要条件p…
-
高中数学理科选修2-2知识点总结
第一章导数及其应用一.导数概念的引入1.导数的物理意义:瞬时速率。一般的,函数y?f(x)在x?x0处的瞬时变化率是?x?0lim…
-
高中数学选修1-1知识点归纳 (1)
高中数学选修1-1知识点总结第一章简单逻辑用语1、命题:用语言、符号或式子表达的,可以判断真假的陈述句.真命题:判断为真的语句.假…
-
高中数学选修2-2知识点总结
导数及其应用一.导数概念的引入数学选修2-2知识点总结1.导数的物理意义:瞬时速率。一般的,函数y?f(x)在x?x0处的瞬时变化…
-
高二数学选修2-1知识点总结
高二数学上期末复习部分知识点概要20xx15高二数学选修21知识点1命题用语言符号或式子表达的可以判断真假的陈述句真命题判断为真的…
-
高二数学总结(选修2-2_2-3知识点)
高二第二学期理科数学总结一、导数1、导数定义:f(x)在点x0处的导数记作;2、几何意义:切线斜率;物理意义:瞬时速度;3、常见函…