解析几何知识点总结
抛物线的标准方程、图象及几何性质:

关于抛物线知识点的补充:
1、定义:
2、几个概念:
① p的几何意义:焦参数p是焦点到准线的距离,故p为正数;
② 焦点的非零坐标是一次项系数的;
③ 方程中的一次项的变量与对称轴的名称相同,一次项的系数符号决定抛物线的开口方向。
④ 通径:2p
3、如: 是过抛物线
是过抛物线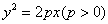 焦点
焦点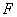 的弦,
的弦,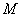 是
是 的中点,
的中点,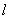 是抛物线的准线,
是抛物线的准线,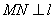 ,
,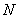 为垂足,
为垂足, ,
,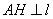 ,
,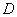 ,
,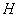 为垂足,求证:
为垂足,求证:
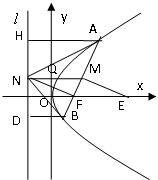 (1)
(1)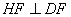 ;
;
(2) ;
;
(3)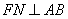 ;
;
(4)设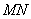 交抛物线于
交抛物线于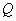 ,则
,则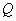 平分
平分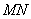 ;
;
(5)设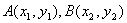 ,则
,则 ,
,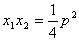 ;
;
(6)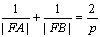 ;
;
(7) 三点在一条直线上
三点在一条直线上
(8)过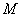 作
作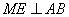 ,
, 交
交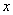 轴于
轴于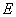 ,求证:
,求证: ,
,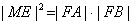 ;
;
关于双曲线知识点的补充:
1、 双曲线的定义:平面内与两个定点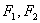 的距离的差的绝对值等于常数(小于
的距离的差的绝对值等于常数(小于 )的点的轨迹。
)的点的轨迹。
第二定义:平面内与一个定点的距离和到一条定直线的距离的比是常数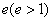 的点的轨迹。两个定点为双曲线的焦点,焦点间距离叫做焦距;定直线叫做准线。常数叫做离心率。
的点的轨迹。两个定点为双曲线的焦点,焦点间距离叫做焦距;定直线叫做准线。常数叫做离心率。
注意: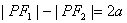 与
与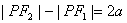 (
(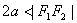 )表示双曲线的一支。
)表示双曲线的一支。  表示两条射线;
表示两条射线;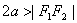 没有轨迹;
没有轨迹;
2、 双曲线的标准方程
①焦点在x轴上的方程: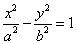 (a>0,b>0); ②焦点在y轴上的方程:
(a>0,b>0); ②焦点在y轴上的方程: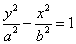 (a>0,b>0);
(a>0,b>0);
③当焦点位置不能确定时,也可直接设椭圆方程为:mx2-ny2=1(m·n<0);
④双曲线的渐近线:改1为0,分解因式则可得两条渐近线之方程.
3、双曲线的渐近线:
①求双曲线 的渐近线,可令其右边的1为0,即得
的渐近线,可令其右边的1为0,即得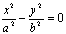 ,因式分解得到。②与双曲线
,因式分解得到。②与双曲线 共渐近线的双曲线系方程是
共渐近线的双曲线系方程是 ;
;
4、等轴双曲线: 为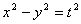 ,其离心率为
,其离心率为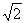
5、共轭双曲线:
6、几个概念:
①焦准距:; ②通径:; ③等轴双曲线x2-y2=l (l∈R,l≠0):渐近线是y=±x,离心率为:;④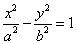 焦点三角形的面积:b2cot (其中∠F1PF2=q);
焦点三角形的面积:b2cot (其中∠F1PF2=q);
⑤弦长公式:|AB|= ;⑥注意;椭圆中:c2=a2-b2,而在双曲线中:c2=a2+b2,
;⑥注意;椭圆中:c2=a2-b2,而在双曲线中:c2=a2+b2,
双曲线的图象及几何性质:

7、直线与双曲线的位置关系:讨论双曲线与直线的位置关系时通常有两种处理方法:①代数法:②、数形结合法。
8、双曲线中的定点、定值及参数的取值范围问题:
①定点、定值问题:通常有两种处理方法:第一种方法Þ是从特殊入手,先求出定点(或定值),再证明这个点(值)与变量无关;第二种方法Þ是直接推理、计算;并在计算的过程中消去变量,从而得到定点(定值)。
②关于最值问题:常见解法有两种:代数法与几何法。若题目中的条件和结论能明显体现几何特征及意义,则考虑利用图形的性质来解决,这就是几何法;若题目中的条件和结论难以体现一种明确的函数关系,则可首先建立目标函数,再求这个函数的最值,求函数的最值常用的方法有配方法、判别式法、重要不等式法、函数的单调性法等。
③参数的取值范围问题:此类问题的讨论常用的方法有两种:第一种是不等式(组)求解法Þ根据题意结合图形列出所讨论的参数适合的不等式(组),通过解不等式再得出参数的变化范围;第二种是函数的值域求解法:把所讨论的参数表示为某个变量的函数,通过讨论函数的值域求得参数的变化范围。
关于椭圆知识点的补充:
1、椭圆的标准方程:
① 焦点在x轴上的方程: (a>b>0); ②焦点在y轴上的方程:
(a>b>0); ②焦点在y轴上的方程: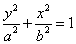 (a>b>0);
(a>b>0);
③当焦点位置不能确定时,也可直接设椭圆方程为:mx2+ny2=1(m>0,n>0); ④、参数方程:

2、椭圆的定义:平面内与两个定点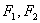 的距离的和等于常数(大于
的距离的和等于常数(大于 )的点的轨迹。
)的点的轨迹。
第二定义:平面内与一个定点的距离和到一条定直线的距离的比是常数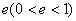 的点的轨迹。 =e (椭圆的焦半径公式:|PF1|=a+ex0, |PF2|=a-ex0)其中:两个定点叫做椭圆的焦点,焦点间的距离叫做焦距;定直线叫做准线。 常数叫做离心率。
的点的轨迹。 =e (椭圆的焦半径公式:|PF1|=a+ex0, |PF2|=a-ex0)其中:两个定点叫做椭圆的焦点,焦点间的距离叫做焦距;定直线叫做准线。 常数叫做离心率。
注意:  表示椭圆;
表示椭圆;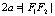 表示线段
表示线段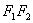 ;
; 没有轨迹;
没有轨迹;
3、 焦准距:; 4、通径:; 5、点与椭圆的位置关系; 6、 焦点三角形的面积:b2tan (其中∠F1PF2=q);
焦点三角形的面积:b2tan (其中∠F1PF2=q);
7、弦长公式:|AB|=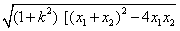 ; 8、 椭圆在点P(x0,y0)处的切线方程:
; 8、 椭圆在点P(x0,y0)处的切线方程: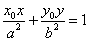 ;
;
9、直线与椭圆的位置关系:
凡涉及直线与椭圆的问题,通常设出直线与椭圆的方程,将二者联立,消去x或y,得到关于y或x的一元二次方程,再利用根与系数的关系及根的判别式等知识来解决,需要有较强的综合应用知识解题的能力。
10、椭圆中的定点、定值及参数的取值范围问题:
①定点、定值问题:通常有两种处理方法:第一种方法Þ是从特殊入手,先求出定点(或定值),再证明这个点(值)与变量无关;第二种方法Þ是直接推理、计算;并在计算的过程中消去变量,从而得到定点(定值)。
②关于最值问题:常见解法有两种:代数法与几何法。若题目中的条件和结论能明显体现几何特征及意义,则考虑利用图形的性质来解决,这就是几何法;若题目中的条件和结论难以体现一种明确的函数关系,则可首先建立目标函数,再求这个函数的最值,求函数的最值常用的方法有配方法、判别式法、重要不等式法、函数的单调性法等。
③参数的取值范围问题:此类问题的讨论常用的方法有两种:第一种是不等式(组)求解法Þ根据题意结合图形列出所讨论的参数适合的不等式(组),通过解不等式(组)得出参数的变化范围;第二种Þ是函数的值域求解法:把所讨论的参数表示为某个变量的函数,通过讨论函数的值域求得参数的变化范围
椭圆图象及几何性质:

第二篇:解析几何知识点总结
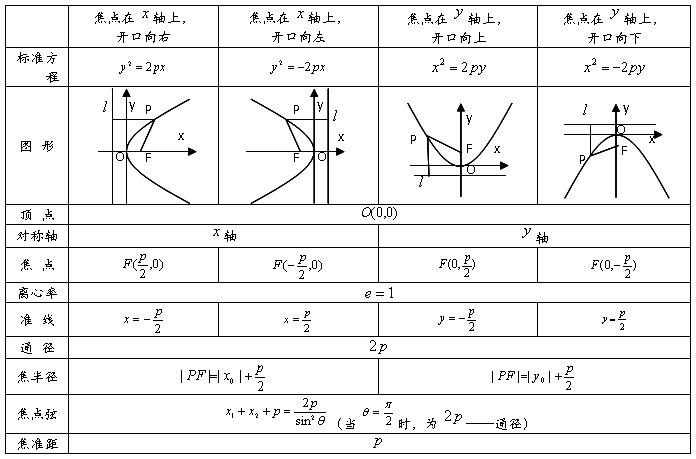
抛物线的标准方程、图象及几何性质: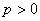
1.抛物线的概念
平面内与一定点F和一条定直线l的距离相等的点的轨迹叫做抛物线(定点F不在定直线l上)。定点F叫做抛物线的焦点,定直线l叫做抛物线的准线。
方程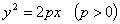 叫做抛物线的标准方程。
叫做抛物线的标准方程。
注意:它表示的抛物线的焦点在x轴的正半轴上,焦点坐标是F(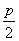 ,0),它的准线方程是
,0),它的准线方程是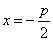 ;
;
2.抛物线的性质
一条抛物线,由于它在坐标系的位置不同,方程也不同,有四种不同的情况,所以抛物线的标准方程还有其他几种形式: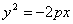 ,
,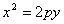 ,
,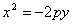 .这四种抛物线的图形、标准方程、焦点坐标以及准线方程。
.这四种抛物线的图形、标准方程、焦点坐标以及准线方程。
说明:(1)通径:过抛物线的焦点且垂直于对称轴的弦称为通径;
(2)抛物线的几何性质的特点:有一个顶点,一个焦点,一条准线,一条对称轴,无对称中心,没有渐近线;
(3)注意强调 的几何意义:是焦点到准线的距离。
的几何意义:是焦点到准线的距离。
题型1:抛物线
例1.(1))焦点到准线的距离是2;
(2)已知抛物线的焦点坐标是F(0,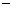 2),求它的标准方程
2),求它的标准方程
【解析】(1)y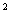 =4x,y
=4x,y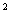 =
=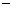 4x,x
4x,x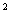 =4y,x
=4y,x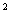 =
=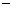 4y;
4y;
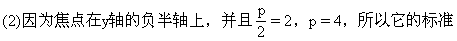
方程是x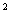 =
=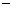 8y。
8y。
点评:由于抛物线的标准方程有四种形式,且每一种形式中都只含一个系数p,因此只要给出确定p的一个条件,就可以求出抛物线的标准方程。当抛物线的焦点坐标或准线方程给定以后,它的标准方程就唯一确定了;若抛物线的焦点坐标或准线方程没有给定,则所求的标准方程就会有多解。
题型2:抛物线的性质
例2.(1)若抛物线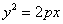 的焦点与椭圆
的焦点与椭圆 的右焦点重合,则
的右焦点重合,则 的值为( )
的值为( )
A. B.
B. C.
C. D.
D.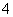
(2)抛物线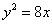 的准线方程是( )
的准线方程是( )
(A) 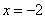 (B)
(B) 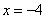 (C)
(C)  (D)
(D) 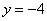
(3)(2009湖南卷文)抛物线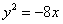 的焦点坐标是( )
的焦点坐标是( )
A.(2,0) B.(- 2,0) C.(4,0) D.(- 4,0)
【解析】(1)椭圆 的右焦点为(2,0),所以抛物线
的右焦点为(2,0),所以抛物线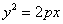 的焦点为(2,0),则
的焦点为(2,0),则 ,故选D;
,故选D;
(2)2p=8,p=4,故准线方程为x=-2,选A;
(3)由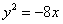 ,易知焦点坐标是
,易知焦点坐标是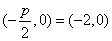 ,故选B.
,故选B.
点评:考察抛物线几何要素如焦点坐标、准线方程的题目根据定义直接计算机即可。
例3.(1)(全国卷I)抛物线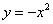 上的点到直线
上的点到直线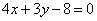 距离的最小值是( )
距离的最小值是( )
A.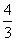 B.
B.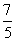 C.
C.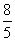 D.
D.
(2)对于顶点在原点的抛物线,给出下列条件:
①焦点在y轴上;
②焦点在x轴上;
③抛物线上横坐标为1的点到焦点的距离等于6;
④抛物线的通径的长为5;
⑤由原点向过焦点的某条直线作垂线,垂足坐标为(2,1)。
能使这抛物线方程为y2=10x的条件是 .(要求填写合适条件的序号)
(3)对于抛物线y2=4x上任意一点Q,点P(a,0)都满足|PQ|≥|a|,则a的取值范围是( )
A.(-∞,0) B.(-∞,2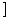 C.[0,2] D.(0,2)
C.[0,2] D.(0,2)
【解析】(1)设抛物线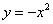 上一点为(m,-m2),该点到直线
上一点为(m,-m2),该点到直线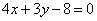 的距离为
的距离为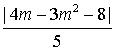 ,当m=
,当m=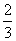 时,取得最小值为
时,取得最小值为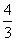 ,选A;
,选A;
(2)答案:②,⑤
从抛物线方程易得②,分别按条件③、④、⑤计算求抛物线方程,从而确定⑤。
(3)答案:B
设点Q的坐标为(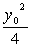 ,y0),
,y0),
由 |PQ|≥|a|,得y02+(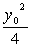 -a)2≥a2.
-a)2≥a2.
整理,得:y02(y02+16-8a)≥0,
∵y02≥0,∴y02+16-8a≥0.
即a≤2+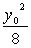 恒成立.而2+
恒成立.而2+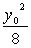 的最小值为2.
的最小值为2.
∴a≤2.选B。
点评:抛物线问题多考察一些距离、最值及范围问题。
关于双曲线知识点的补充:
1、 双曲线的定义:平面内与两个定点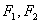 的距离的差的绝对值等于常数(小于
的距离的差的绝对值等于常数(小于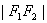 )的点的轨迹。
)的点的轨迹。
第二定义:平面内与一个定点的距离和到一条定直线的距离的比是常数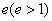 的点的轨迹。两个定点为双曲线的焦点,焦点间距离叫做焦距;定直线叫做准线。常数叫做离心率。
的点的轨迹。两个定点为双曲线的焦点,焦点间距离叫做焦距;定直线叫做准线。常数叫做离心率。
注意: 与
与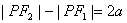 (
(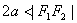 )表示双曲线的一支。
)表示双曲线的一支。 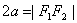 表示两条射线;
表示两条射线;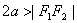 没有轨迹;
没有轨迹;
2、 双曲线的标准方程
①焦点在x轴上的方程: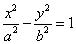 (a>0,b>0); ②焦点在y轴上的方程:
(a>0,b>0); ②焦点在y轴上的方程: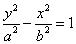 (a>0,b>0);
(a>0,b>0);
③当焦点位置不能确定时,也可直接设椭圆方程为:mx2-ny2=1(m·n<0);
④双曲线的渐近线:改1为0,分解因式则可得两条渐近线之方程.
3、双曲线的渐近线:
①求双曲线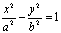 的渐近线,可令其右边的1为0,即得
的渐近线,可令其右边的1为0,即得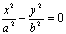 ,因式分解得到。②与双曲线
,因式分解得到。②与双曲线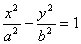 共渐近线的双曲线系方程是
共渐近线的双曲线系方程是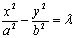 ;
;
4、等轴双曲线: 为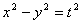 ,其离心率为
,其离心率为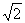
5、共轭双曲线:
6、几个概念:
①焦准距:; ②通径:; ③等轴双曲线x2-y2=l (l∈R,l≠0):渐近线是y=±x,离心率为:;④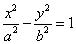 焦点三角形的面积:b2cot (其中∠F1PF2=q);
焦点三角形的面积:b2cot (其中∠F1PF2=q);
⑤弦长公式:|AB|=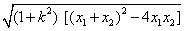 ;⑥注意;椭圆中:c2=a2-b2,而在双曲线中:c2=a2+b2,
;⑥注意;椭圆中:c2=a2-b2,而在双曲线中:c2=a2+b2,
双曲线的图象及几何性质:
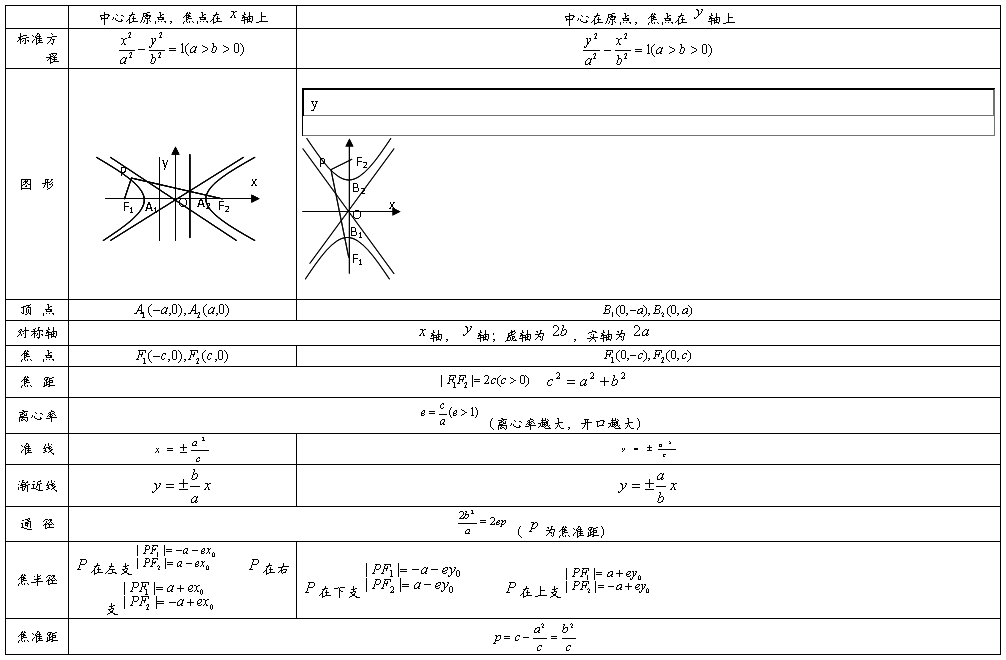
7、直线与双曲线的位置关系:讨论双曲线与直线的位置关系时通常有两种处理方法:①代数法:②、数形结合法。
8、双曲线中的定点、定值及参数的取值范围问题:
①定点、定值问题:通常有两种处理方法:第一种方法Þ是从特殊入手,先求出定点(或定值),再证明这个点(值)与变量无关;第二种方法Þ是直接推理、计算;并在计算的过程中消去变量,从而得到定点(定值)。
②关于最值问题:常见解法有两种:代数法与几何法。若题目中的条件和结论能明显体现几何特征及意义,则考虑利用图形的性质来解决,这就是几何法;若题目中的条件和结论难以体现一种明确的函数关系,则可首先建立目标函数,再求这个函数的最值,求函数的最值常用的方法有配方法、判别式法、重要不等式法、函数的单调性法等。
③参数的取值范围问题:此类问题的讨论常用的方法有两种:第一种是不等式(组)求解法Þ根据题意结合图形列出所讨论的参数适合的不等式(组),通过解不等式再得出参数的变化范围;第二种是函数的值域求解法:把所讨论的参数表示为某个变量的函数,通过讨论函数的值域求得参数的变化范围。
关于椭圆知识点的补充:
1、椭圆的标准方程:
① 焦点在x轴上的方程: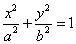 (a>b>0); ②焦点在y轴上的方程:
(a>b>0); ②焦点在y轴上的方程: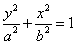 (a>b>0);
(a>b>0);
③当焦点位置不能确定时,也可直接设椭圆方程为:mx2+ny2=1(m>0,n>0); ④、参数方程: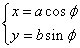

2、椭圆的定义:平面内与两个定点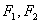 的距离的和等于常数(大于
的距离的和等于常数(大于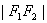 )的点的轨迹。
)的点的轨迹。
第二定义:平面内与一个定点的距离和到一条定直线的距离的比是常数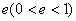 的点的轨迹。 =e (椭圆的焦半径公式:|PF1|=a+ex0, |PF2|=a-ex0)其中:两个定点叫做椭圆的焦点,焦点间的距离叫做焦距;定直线叫做准线。 常数叫做离心率。
的点的轨迹。 =e (椭圆的焦半径公式:|PF1|=a+ex0, |PF2|=a-ex0)其中:两个定点叫做椭圆的焦点,焦点间的距离叫做焦距;定直线叫做准线。 常数叫做离心率。
注意: 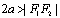 表示椭圆;
表示椭圆;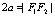 表示线段
表示线段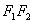 ;
;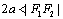 没有轨迹;
没有轨迹;
3、 焦准距:; 4、通径:; 5、点与椭圆的位置关系; 6、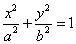 焦点三角形的面积:b2tan (其中∠F1PF2=q);
焦点三角形的面积:b2tan (其中∠F1PF2=q);
7、弦长公式:|AB|= ; 8、 椭圆在点P(x0,y0)处的切线方程:
; 8、 椭圆在点P(x0,y0)处的切线方程: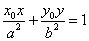 ;
;
9、直线与椭圆的位置关系:
凡涉及直线与椭圆的问题,通常设出直线与椭圆的方程,将二者联立,消去x或y,得到关于y或x的一元二次方程,再利用根与系数的关系及根的判别式等知识来解决,需要有较强的综合应用知识解题的能力。
10、椭圆中的定点、定值及参数的取值范围问题:
①定点、定值问题:通常有两种处理方法:第一种方法Þ是从特殊入手,先求出定点(或定值),再证明这个点(值)与变量无关;第二种方法Þ是直接推理、计算;并在计算的过程中消去变量,从而得到定点(定值)。
②关于最值问题:常见解法有两种:代数法与几何法。若题目中的条件和结论能明显体现几何特征及意义,则考虑利用图形的性质来解决,这就是几何法;若题目中的条件和结论难以体现一种明确的函数关系,则可首先建立目标函数,再求这个函数的最值,求函数的最值常用的方法有配方法、判别式法、重要不等式法、函数的单调性法等。
③参数的取值范围问题:此类问题的讨论常用的方法有两种:第一种是不等式(组)求解法Þ根据题意结合图形列出所讨论的参数适合的不等式(组),通过解不等式(组)得出参数的变化范围;第二种Þ是函数的值域求解法:把所讨论的参数表示为某个变量的函数,通过讨论函数的值域求得参数的变化范围
椭圆图象及几何性质:
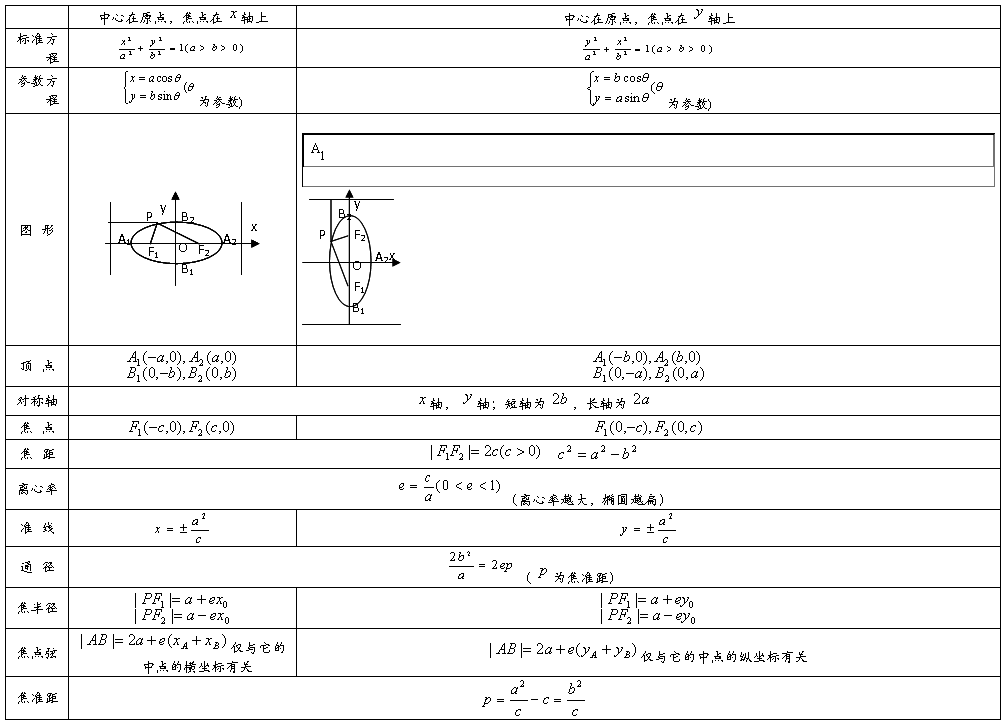
-
高考知识点汇总之解析几何模块
邹维政解析几何知识点总结解析几何总结一直线1直线的倾斜角一条直线向上的方向与X轴的正方向所成的最小正角2范围03直线的斜率当倾斜角…
-
解析几何知识点总结
抛物线的标准方程图象及几何性质p0关于抛物线知识点的补充1定义2几个概念p的几何意义焦参数p是焦点到准线的距离故p为正数14方程中…
-
平面解析几何知识点总结
平面解析几何基本要求掌握两条直线平行垂直的条件能根据直线方程判断两条直线的位置关系掌握两条直线的夹角公式到角公式和点到直线的距离公…
-
平面解析几何知识点总结
平面解析几何基本要求掌握两条直线平行垂直的条件能根据直线方程判断两条直线的位置关系掌握两条直线的夹角公式到角公式和点到直线的距离公…
-
解析几何知识点总结
抛物线的标准方程图象及几何性质p0关于抛物线知识点的补充1定义2几个概念p的几何意义焦参数p是焦点到准线的距离故p为正数焦点的非零…
-
高中解析几何知识点汇总
直线与圆1.直线方程:⑴点斜式:y?y??k(x?x?)⑵斜截式:y?kx?b;⑶截距式:xy??1;ab⑷两点式:y?y1x?x…
-
解析几何知识总结
一直线与圆知识总结1直线的倾斜角2直线方程的几种形式点斜式截距式两点式斜切式3两条直线平行l推论如果两条直线l1l2的倾斜角为12…
-
解析几何知识点总结
淮上陌客20xx326抛物线的标准方程图象及几何性质p0淮上陌客20xx326关于抛物线知识点的补充1定义2几个概念p的几何意义焦…
-
解析几何知识点总结
抛物线的标准方程图象及几何性质p0关于抛物线知识点的补充1定义2几个概念p的几何意义焦参数p是焦点到准线的距离故p为正数焦点的非零…
-
高中数学知识点总结之平面向量与空间解析几何(经典必看)
56你对向量的有关概念清楚吗1向量既有大小又有方向的量2向量的模有向线段的长度a3单位向量a01a04零向量000aa长度相等5相…
-
立体几何知识点总结
一、平面通常用一个平行四边形来表示.平面常用希腊字母α、β、γ?或拉丁字母M、N、P来表示,也可用表示平行四边形的两个相对顶点字母…