导数大题方法总结

一 总论

一般来说，导数的大题有两到三问。每一个小问的具体题目虽然并不固定，但有相当的规律可循，所以在此我进行了一个答题方法的总结。

二 主流题型及其方法

*（1）求函数中某参数的值或给定参数的值求导数或切线

一般来说，一到比较温和的导数题的会在第一问设置这样的问题：若f(x)在x = k时取得极值，试求所给函数中参数的值；或者是f(x)在(a , f(a))处的切线与某已知直线垂直，试求所给函数中参数的值等等很多条件。虽然会有很多的花样，但只要明白他们的本质是考察大家求导数的能力，就会轻松解决。这一般都是用来送分的，所以遇到这样的题，一定要淡定，方法是：

先求出所给函数的导函数，然后利用题目所给的已知条件，以上述第一种情形为例：令x = k，f(x)的导数为零，求解出函数中所含的参数的值，然后检验此时是否为函数的极值。

注意：①导函数一定不能求错，否则不只第一问会挂，整个题目会一并挂掉。保证自己求导不会求错的最好方法就是求导时不要光图快，一定要小心谨慎，另外就是要将导数公式记牢，不能有马虎之处。②遇到例子中的情况，一道要记得检验，尤其是在求解出来两个解的情况下，更要检验，否则有可能会多解，造成扣分，得不偿失。所以做两个字来概括这一类型题的方法就是：淡定。别人送分，就不要客气。③求切线时，要看清所给的点是否在函数上，若不在，要设出切点，再进行求解。切线要写成一般式。

*（2）求函数的单调性或单调区间以及极值点和最值

一般这一类题都是在函数的第二问，有时也有可能在第一问，依照题目的难易来定。这一类题问法都比较的简单，一般是求f(x)的单调（增减）区间或函数的单调性，以及函数的极大（小）值或是笼统的函数极值。一般来说，由于北京市高考不要求二阶导数的计算，所以这类题目也是送分题，所以做这类题也要淡定。这类问题的方法是：

首先写定义域，求函数的导函数，并且进行通分，变为假分式形式。往下一般有两类思路，一是走一步看一步型，在行进的过程中，一点点发现参数应该讨论的范围，一步步解题。这种方法个人认为比较累，而且容易丢掉一些情况没有进行讨论，所以比较推荐第二种方法，就是所谓的一步到位型，先通过观察看出我们要讨论的参数的几个必要的临介值，然后以这些值为分界点，分别就这些临界点所分割开的区间进行讨论，这样不仅不会漏掉一些对参数必要的讨论，而且还会是自己做题更有条理，更为高效。

极值的求法比较简单，就是在上述步骤的基础上，令导函数为零，求出符合条件的根，然后进行列表，判断其是否为极值点并且判断出该极值点左右的单调性，进而确定该点为极大值还是极小值，最后进行答题。

最值问题是建立在极值的基础之上的，只是有些题要比较极值点与边界点的大小，不能忘记边界点。

注意:①要注意问题，看题干问的是单调区间还是单调性，极大值还是极小值，这决定着你最后如何答题。还有最关键的，要注意定义域，有时题目不会给出定义域，这时就需要你自己写出来。没有注意定义域问题很严重。②分类要准，不要慌张。③求极值一定要列表，不能使用二阶导数，否则只有做对但不得分的下

场。

*（3）恒成立或在一定条件下成立时求参数范围

这类问题一般都设置在导数题的第三问，也就是最后一问，属于有一定难度的问题。这就需要我们一定的综合能力。不仅要对导数有一定的理解，而且对于一些不等式、函数等的知识要有比较好的掌握。这一类题目不是送分题，属于扣分题，但掌握好了方法，也可以百发百中。方法如下：

做这类恒成立类型题目或者一定范围内成立的题目的核心的四个字就是：分离变量。一定要将所求的参数分离出来，否则后患无穷。有些人总是认为不分离变量也可以做。一些简单的题目诚然可以做，但到了真正的难题，分离变量的优势立刻体现，它可以规避掉一些极为繁琐的讨论，只用一些简单的代数变形可以搞定，而不分离变量就要面临着极为麻烦的讨论，不仅浪费时间，而且还容易出差错。所以面对这样的问题，分离变量是首选之法。当然有的题确实不能分离变量，那么这时就需要我们的观察能力，如果还是没有简便方法，那么才会进入到讨论阶段。

分离变量后，就要开始求分离后函数的最大或者最小值，那么这里就要重新构建一个函数，接下来的步骤就和（2）中基本相同了。

注意：①分离时要注意不等式的方向，必要的时候还是要讨论。②要看清是求分离后函数的最大值还是最小值，否则容易搞错。③分类要结合条件看，不能抛开大前提自己胡搞一套。

最后，这类题还需要一定的不等式知识，比如均值不等式，一些高等数学的不等数等等。这就需要我们有足够的知识储备，这样做起这样的题才能更有效率。

（4）构造新函数对新函数进行分析

这类题目题型看似复杂，但其实就是在上述问题之上多了一个步骤，就是将上述的函数转化为了另一个函数，并没有本质的区别，所以这里不再赘述。

（5）零点问题

这类题目在选择填空中更容易出现，因为这类问题虽然不难，但要求学生对与极值和最值问题有更好的了解，它需要我们结合零点，极大值极小值等方面综合考虑，所以更容易出成填空题和选择题。如果出成大题，大致方法如下： 先求出函数的导函数，然后分析求解出函数的极大值与极小值，然后结合题目中所给的信息与条件，求出在特定区间内，极大值与极小值所应满足的关系，然后求解出参数的范围。

三 总结

以上就是导数大题的主要题型及方法，当然有很多题型不能完全的照顾到，有很多的创新题型没有涉及，那么如何解决这个问题呢？就是我们要明白导数题的核心是什么。导数题的核心就是参数，就是对参数的把握，而对参数的理解与分析正是每一道题目的核心。只要我们能够从参数入手，能够对参数进行分析，那么不论一道题有多么的繁琐，我们都能够把握这道题的主线，能有一个明确的脉络，做出题目。所以我总结的导数题的八字大纲，不一定对，但我认为对于解决北京市的高考题有一定的帮助，那就是“分离变量，一步到位”。一切的一切，都应该围绕着参量来展开。相信导数虽然是第18或者19题，但也一定会被我们大家淡定的斩于马下。

 

第二篇：导数各类题型方法总结

导数各种题型方法总结

请同学们高度重视：

首先，关于二次函数的不等式恒成立的主要解法：

1、分离变量；2变更主元；3根分布；4判别式法

5、二次函数区间最值求法：（1）对称轴（重视单调区间） 与定义域的关系 （2）端点处和顶点是最值所在

其次，分析每种题型的本质，你会发现大部分都在解决“不等式恒成立问题”以及“充分应用数形结合思想”，创建不等关系求出取值范围。 最后，同学们在看例题时，请注意寻找关键的等价变形和回归的基础

一、基础题型：函数的单调区间、极值、最值；不等式恒成立；

1、此类问题提倡按以下三个步骤进行解决：

第一步：令f'(x)?0得到两个根；

第二步：画两图或列表；

第三步：由图表可知；

其中不等式恒成立问题的实质是函数的最值问题，

2、常见处理方法有三种：

第一种：分离变量求最值-----用分离变量时要特别注意是否需分类讨论（>0,=0,<0） 第二种：变更主元（即关于某字母的一次函数）-----（已知谁的范围就把谁作为主元）； （请同学们参看2010省统测2）

例1：设函数y?f(x)在区间D上的导数为f?(x)，f?(x)在区间D上的导数为g(x)，若在区间D上，g(x)?0恒成立，则称函数y?f(x)在区间D上为“凸函数”，已知实数m是常数，f(x)?x4

12?mx

63?3x

22

（1）若y?f(x)在区间?0,3?上为“凸函数”，求m的取值范围；

（2）若对满足m?2的任何一个实数m，函数f(x)在区间?a,b?上都为“凸函数”，求b?a的最大值.

解:由函数f(x)?

2x412?mx63?3x22 得f?(x)?x33?mx22?3x ?g(x)?x?mx?3

（1） ?y?f(x)在区间?0,3?上为“凸函数”，

则 ?g(x)?x?mx?3?0 在区间[0,3]上恒成立

解法一：从二次函数的区间最值入手：等价于gmax(x)?0

?g(0)?

???g(3)0???30???m?2 0??9m3??302

解法二：分离变量法：

2∵ 当x?0时, ?g(x)?x?mx?3??3?0恒成立,

2 当0?x?3时, g(x)?x?mx?3?0恒成立

等价于m?x?3

x

3

x2?x?3x的最大值（0?x?3）恒成立， 而h(x)?x?

?m?2 （0?x?3）是增函数，则hmax(x)?h(3)?2

(2)∵当m?2时f(x)在区间?a,b?上都为“凸函数” 则等价于当m?2时g(x)?x2?mx?3?0 恒成立 变更主元法

再等价于F(m)?mx?x2?3?0在m?2恒成立（视为关于m的一次函数最值问题）

20?F(?2)?0???x2?x??3

??????1?x?1 2??F(2)?0?2x?x?3?0

?b?a?2 请同学们参看2010第三次周考：

例2：设函数f(x)??1

3x?2ax32?3ax?b(0?a?1,b?R) 2

（Ⅰ）求函数f（x）的单调区间和极值； （Ⅱ）若对任意的x?[a?1,a?2],不等式f?(x)?a恒成立，求a的取值范围. （二次函数区间最值的例子） 解：（Ⅰ）f?(x)??x?4ax?3a???x?3a??x?a? 22?0?a?1

令f?(x)?0,得f(x)令f?(x)?0,得f(x)的单调递减区间为（－?，a）和（3a，+?）

∴当x=a时，f(x)极小值=?3

4a?b; 当x=3a时，f(x)极大值=b. 3

22 （Ⅱ）由|f?(x)|≤a，得：对任意的x?[a?1,a?2],?a?x?4ax?3a?a恒成立①

?gmax(x)?a22则等价于g(x)这个二次函数? g(x)?x?4ax?3a的对称轴x?2a ?gmin(x)??a

?0?a?1 , a?1?a?a?2a（放缩法）

即定义域在对称轴的右边，g(x)这个二次函数的最值问题：单调增函数的最值问题。

g(x)?x?4ax?3a在[a?1,a?2]上是增函数.

g(x)max?g(a?2)??2a?1.

g(x)min?g(a?1)??4a?4.22∴

?1,

x?aa?2? 于是，对任意x?[a?1,a?2]，不等式①恒成立，等价于

?g(a?2)??4a?4?a,4解得?a?1. ?5?g(a?1)??2a?1??a

又0?a?1,∴4

5?a?1.

点评：重视二次函数区间最值求法：对称轴（重视单调区间）与定义域的关系

第三种：构造函数求最值

题型特征：f(x)?g(x)恒成立?h(x)?f(x)?g(x)?0恒成立；从而转化为第一、二种题型

例3；已知函数f(x)?x3?ax2图象上一点P(1,b)处的切线斜率为?3，

g(x)?x?3t?6

2x?(t?1)x?32(t?0)

（Ⅰ）求a,b的值；

（Ⅱ）当x?[?1,4]时，求f(x)的值域；

（Ⅲ）当x?[1,4]时，不等式f(x)?g(x)恒成立，求实数t的取值范围。

/?f(1)??3?a??3/2解：（Ⅰ）f(x)?3x?2ax∴?， 解得? b??2b?1?a??

（Ⅱ）由（Ⅰ）知，f(x)在[?1,0]上单调递增，在[0,2]上单调递减，在[2,4]上单调递减

又f(?1)??4,f(0)?0,f(2)??4,f(4)?16

∴f(x)的值域是[?4,16] （Ⅲ）令h(x)?f(x)?g(x)??t

2x?(t?1)x?32x?[1,4]

2思路1：要使f(x)?g(x)恒成立，只需h(x)?0，即t(x?2x)?2x?6分离变量

思路2：二次函数区间最值

二、题型一：已知函数在某个区间上的单调性求参数的范围

解法1：转化为f'(x)?0或f'(x)?0在给定区间上恒成立， 回归基础题型

解法2：利用子区间（即子集思想）；首先求出函数的单调增或减区间，然后让所给区间是求的增或减区间的子集；

做题时一定要看清楚“在（m,n）上是减函数”与“函数的单调减区间是（a,b）”，要弄清楚两句话的区别：前者是后者的子集

例4：已知a?R，函数f(x)?1

12x?3a?1

2x?(4a?1)x． 2

（Ⅰ）如果函数g(x)?f?(x)是偶函数，求f(x)的极大值和极小值； （Ⅱ）如果函数f(x)是(??,

解：f?(x)?

??)上的单调函数，求a的取值范围．

14

x?(a?1)x?(4a?1).

112

3

x?3x，f?(x)?

2

（Ⅰ）∵ f?(x)是偶函数，∴ a??1. 此时f(x)? 令f?(x)?0，解得：x??2 列表如下：

14

x?3，

2

3.

可知：f(x)的极大值为f(?23)?43， f(x)的极小值为f(23)??43. （Ⅱ）∵函数f(x)是(??,

∴f?(x)?

??)上的单调函数，

14

x?(a?1)x?(4a?1?)，在给定区间0

2

2

R上恒成立判别式法

则??(a?1)?4?

14

?(4a?1)?a?2a?0， 解得：0?a?2.

2

综上，a的取值范围是{a0?a?2}.

例5、已知函数f(x)?

13x?

3

12

(2?a)x?(1?a)x(a?0).

2

（I）求f(x)的单调区间；

（II）若f(x)在[0，1]上单调递增，求a的取值范围。子集思想

2

（I）f?(x)?x?(2?a)x?1?a?(x?1)(

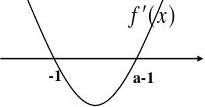
x?1?a).

2

1、当a?0时,f?(x)?(x?1)?0恒成立,

当且仅当x??1时取“=”号，f(x)在(??,??)单调递增。 2、当a?0时,由f?(x)?0,得x1??1,x2?a?1,且x1?x2,

单调增区间：(??,?1)a ,(?1?,? 单调增区间：(?1a,?1 )

（II）当?f(x)在[0,1]上单调递增, 则?0,1?是上述增区间的子集：

1、a?0时，f(x)在(??,??)单调递增 符合题意 2、?0,1???a?1,???，?a?1?0 ?a?1 综上，a的取值范围是[0，1]。

三、题型二：根的个数问题

题1函数f(x)与g(x)（或与x轴）的交点======即方程根的个数问题 解题步骤

第一步：画出两个图像即“穿线图”（即解导数不等式）和“趋势图”即三次函数的大致趋势“是先增后减再增”还是“先减后增再减”； 第二步：由趋势图结合交点个数或根的个数写不等式（组）；主要看极大值和极小值与

0的关

系；

第三步：解不等式（组）即可； 例6、已知函数f(x)?

13x

3

?

(k?1)2

x，g(x)?

2

13

?kx，且f(x)在区间(2,??)上为增函数．

（1） 求实数k的取值范围；

（2） 若函数f(x)与g(x)的图象有三个不同的交点，求实数k的取值范围． 解：（1）由题意f?(x)?x2?(k?1)x ∵f(x)在区间(2,??)上为增函数，

∴f?(x)?x2?(k?1)x?0在区间(2,??)上恒成立（分离变量法）

即k?1?x恒成立，又x?2，∴k?1?2，故k?1∴k的取值范围为k?1 （2）设h(x)?f(x)?g(x)?

h?(x)?x

2

x

3

3

?

(k?1)2

x

2

?kx?

13

，

?(k?1)x?k?(x?k)(x?1)

令h?(x)?0得x?k或x?1由（1）知k?1，

2

①当k?1时，h?(x)?(x?1)?0，h(x)在R上递增，显然不合题意? ②当k?1时，h(x)，h?(x)随x的变化情况如下表：

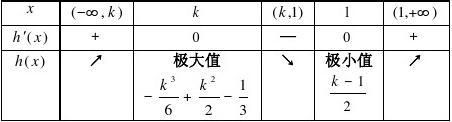
由于故需?

k

3

k?12

?0，欲使f(x)与g(x)的图象有三个不同的交点，即方程h(x)?0有三个不同的实根，

2

6

?

k

2

?

13

?0，即(k?1)(k

2

?k?1

?2k?2)?0 ∴?2，解得k?1?

?k?2k?2?0

3

综上，所求k的取值范围为k?1?3

根的个数知道，部分根可求或已知。 例7、已知函数f(x)?ax?

3

12

x?2x?c

2

（1）若x??1是f(x)的极值点且f(x)的图像过原点，求f(x)的极值；

（2）若g(x)?

1

2

图像恒有含x??1的三个不同交点？若存在，求出实数b的取值范围；否则说明理由。

bx?x?d，在（1）的条件下，是否存在实数b，使得函数g(x)的图像与函数f(x)的

2

解：（1）∵f(x)的图像过原点，则f(0)?0?c?0 f?(x)?3ax2?x?2，

又∵x??1是f(x)的极值点，则f?(?1)?3a?1?2?0?a??1

2

?f?(x)?3x?x?2?(3x?2)(x?1)?0

f极大值(x)?f(?1)?

32

f极小值(x)?f?)?

3

2227

（2）设函数g(x)的图像与函数f(x)的图像恒存在含x??1的三个不同交点，

等价于f(x)?g(x)有含x??1的三个根，即：f(?1)?g(?1)?d??

?x?

33

12

(b?1)

12

x?2x?12

2

12

2

bx?x?

12

2

12

(b?1)整理得：

即：x?(b?1)x?x?

(b?1)?0恒有含x??1的三个不等实根

12

(b?1)x?x?

2

（计算难点来了：）h(x)?x3?

12

(b?1)?0有含x??1的根，

则h(x)必可分解为(x?1)(二次式)?0，故用添项配凑法因式分解，

x?x?x?

3

2

2

12

(b?1)x?x?

2

12

(b?1)?0

1?1?22

x(x?1)??(b?1)x?x?(b?1)??0

2?2?x(x?1)?

1

2

1

?(b?1)x2?2x?(b?1)??0 ?2?

1 ?

)?b(???1)x?? 十字相乘法分解：x2(x?1)??(b?1x

2

1?21?

(x?1)?x?(b?1)x?(b?1)??0

22??

?x?

3

12

(b?1)x?x?

2

2

1212

(b?1)?0恒有含x??1的三个不等实根 (b?1)?0有两个不等于-1的不等实根。

等价于x?

12

(b?1)x?

11?2

??(b?1)?4?(b?1)?0??42???b?(??,?1)?(?1,3)?(3,??

) ?(?1)2?1(b?1)?1(b?1)?0??22

题2：切线的条数问题====以切点x0为未知数的方程的根的个数

例7、已知函数f(x)?ax3?bx2?cx在点x0处取得极小值－4，使其导数f'(x)?0的x的取值范围为(1,3)，求：（1）f(x)的解析式；（2）若过点P(?1,m)可作曲线y?f(x)的三条切线，求实数m的取值范围．

（1）由题意得：f'(x)?3ax2?2bx?c?3a(x?1)(x?3),(a?0)

∴在(??,1)上f'(x)?0；在(1,3)上f'(x)?0；在(3,??)上f'(x)?0 因此f(x)在x0?1处取得极小值?4

∴a?b?c??4①，f'(1)?3a?2b?c?0②，f'(3)?27a?6b?c?0③

?a??1

?由①②③联立得：?b?6，∴f(x)??x3?6x2?9x

?c??9?

（2）设切点Q(t,f(t))，y?f(t)?f,(t)(x?t)

y?(?3t?12t?9)(x?t)?(?t?6t?9t)

?(?3t?12t?9)x?t(3t?12t?9)?t(t?6t?9) ?(?3t?12t?9)x?t(2t?6t)过(?1,m)

m?(?3t?12t?9)(?1)?2t?6t

g(t)?2t?2t?12t?9?m?0 3223222222232

令g'(t)?6t2?6t?12?6(t2?t?2)?0，

求得：t??1,t?2，方程g(t)?0有三个根。

需：??g(?1)?0??2?3?12?9?m?0?m?16????

?g(2)?0?16?12?24?9?m?0?m??11故：?11?m?16；因此所求实数m的范围为：(?11,16) 题3：已知f(x)在给定区间上的极值点个数则有导函数=0的根的个数 解法：根分布或判别式法

例8、

1372解：函数的定义域为R（Ⅰ）当m＝4时，f (x)＝ x－x＋10x， 32

2f?(x)＝x－7x＋10，令f?(x)?0 ， 解得x?5,或x?2.

令f?(x)?0 ， 解得2?x?5

可知函数f(x)的单调递增区间为(??,2)和（5，＋∞），单调递减区间为?2,5?． （Ⅱ）f?(x)＝x2－(m＋3)x＋m＋6,

要使函数y＝f (x)在（1，＋∞）有两个极值点,?f?(x)＝x－(m＋3)x＋m＋6=0的根在（1，＋∞）

2

根分布问题：

?

???(m?3)2?4(m?6)?0;?

则?f?(1)?1?(m?3)?m?6?0;， 解得m＞3 ?m?3??1.?2

例9、已知函数f(x)?

a3x?

3

12

（2）令g(x)＝x，(a?R,a?0)（1）求f(x)的单调区间；

2

14

x＋f

4

（x）（x∈R）有且仅有3个极值点，求a的取值范围． 解：（1）f'(x)?ax2?x?x(ax?1)

当a?0时，令f'(x)?0解得x??所以f(x)的递增区间为(??,?

1a

1a

或x?0，令f(x)?0解得?

1a,0).

1a,??).

'

1a

?x?0，

)?(0,??)，递减区间为(?

1a

?当a?0时，同理可得f(x)的递增区间为(0，)，递减区间为(??,0)?(?

（2）g(x)?

14

x?

4

a3

x?

3

12

x有且仅有3个极值点

2

3222

?g?(x)?x?ax?x?x(x?ax?1)=0有3个根，则x?0或x?ax?1?0，a??2

方程x?ax?1?0有两个非零实根，所以??a?4?0,

?a??2或a?2

22

而当a??2或a?2时可证函数y?g(x)有且仅有3个极值点

其它例题：

1、（最值问题与主元变更法的例子）.已知定义在R上的函数f(x)?ax3?2ax2?b（a?0）在区间??2,1?上的最大值是5，最小值是－11.

（Ⅰ）求函数f(x)的解析式；

（Ⅱ）若t?[?1,1]时，f?(x）?tx?0恒成立，求实数x的取值范围

.

解：（Ⅰ）?f(x)?ax3?2ax2?b,?f'(x)?3ax2?4ax?ax(3x?4)

令f'(x)=0,得x1?0,x2?43???2,1?

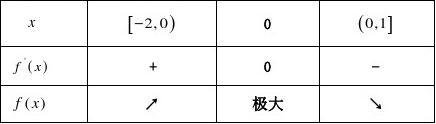
因此f(0)必为最大值,∴f（0）?5因此b?5， ?f(?2)??16a?5,f(1)??a?5,?f(1)?f(?2)， 即f(?2)??16a?5??11，∴a?1，∴ f(x）?x3?2x2?5.

2（Ⅱ）∵f?(x)?3x2?4x，∴f?(x）?tx?0等价于3x?4x?tx?0，

令g(t)?xt?3x2?4x，则问题就是g(t)?0在t?[?1,1]上恒成立时，求实数x的取值范围，

?3x2?5x?0?g(?1)?0为此只需?，即?2， g（1)?0??x?x?0

解得0?x?1，所以所求实数x的取值范围是[0，1].

2、（根分布与线性规划例子）

（1）已知函数f(x)?2

3x?ax?bx?c 32

(Ⅰ) 若函数f(x)在x?1时有极值且在函数图象上的点(0,1)处的切线与直线3x?y?0平行, 求f(x)的解析式；

(Ⅱ) 当f(x)在x?(0,1)取得极大值且在x?(1,2)取得极小值时, 设点M(b?2,a?1)所在平面区域为S, 经过原点的直线L将S分为面积比为1:3的两部分, 求直线L的方程.

2解： (Ⅰ). 由f?(x)?2x?2ax?b, 函数f(x)在x?1时有极值 ,

∴ 2a?b?2?0

∵ f(0)?1 ∴ c?1

又∵ f(x)在(0,1)处的切线与直线3x?y?0平行,

∴ f?(0)?b??3 故 a?

∴ f(x)?2

3x?312 1

2x?3x?1 ……………………. 7分 2

2 (Ⅱ) 解法一: 由f?(x)?2x?2ax?b 及f(x)在x?(0,1)取得极大值且在x?(1,2)取得极小值,

??∴ ?

??

f?(0)?0

?b?0?

f?(1)?0 即 ?2a?b?2?0 令M(x,

?4a?b?8?0f?(2)?0?

?x?b?2

y), 则 ?

y?a?1?

?x?2?0

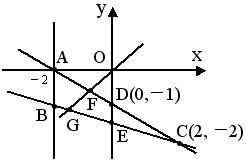
?a?y?1?∴ ? ∴ ?2y?x?2?0 故点M所在平面区域S为如图△ABC,

?b?x?2?4y?x?6?0

?

易得A(?2,0), B(?2,?1), C(2,?2), D(0,?1), E(0,?

32

), S?ABC?2

同时DE为△ABC的中位线, S?DEC?∴ 所求一条直线L的方程为:

x?0

13

S四边形ABED

另一种情况设不垂直于x轴的直线L也将S分为面积比为1:3的两部分, 设直线L方程为y?kx,它与AC,BC分别交于F、G, 则 k?0, S四边形DEGF?1

由 ?

?y?kx?2y?x?2?0

得点F的横坐标为: xF??

22k?1

?y?kx6

由 ? 得点G的横坐标为: xG??

4y?x?6?04k?1?

∴S四边形DEGF?S?OGE?S?OFD ?解得: k?

12

12

?

32

?

64k?1

?

12

?1?

22k?1

12

?1即 16k2?2k?5?0

或 k??

58

(舍去) 故这时直线方程为: y?

12

x

综上,所求直线方程为: x?0或y?x .…………….………….12分

2

(Ⅱ) 解法二: 由f?(x)?2x?2ax?b 及f(x)在x?(0,1)取得极大值且在x?(1,

2)取得极小值,

??∴ ?

??

f?(0)?0

?b?0?

f?(1)?0 即 ?2a?b?2?0 令M(x,

?4a?b?8?0f?(2)?0?

?x?b?2

y), 则 ?

y?a?1?

?x?2?0

?a?y?1?∴ ? ∴ ?2y?x?2?0 故点M所在平面区域S为如图△ABC,

?b?x?2?4y?x?6?0

?

易得A(?2,0), B(?2,?1), C(2,?2), D(0,?1), E(0,?

32

), S?ABC?2

同时DE为△ABC的中位线, S?DEC?

13

S四边形ABED ∴所求一条直线L的方程为: x?0

另一种情况由于直线BO方程为: y?

12

x, 设直线BO与AC交于H ,

1?y?x?由 ? 得直线L与AC交点为: H(?1,2

?2y?x?2?0?

12

12

12

?

12

)

∵ S?ABC?2, S?DEC?

??2?

12

, S?ABH?S?ABO?S?AOH?

12

?2?1?

12

?2?

12

?

12

∴ 所求直线方程为: x?0 或y?x

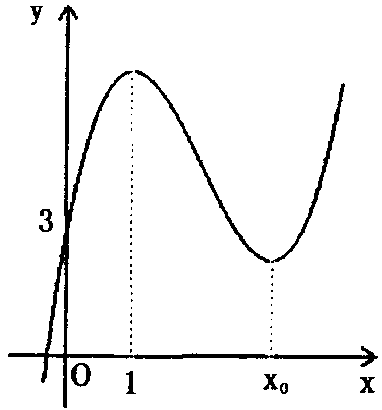
3、（根的个数问题）已知函数f(x)?ax3?bx2?(c?3a?2b)x?d (a?0)的图象如图所示。

（Ⅰ）求c、d的值；

（Ⅱ）若函数f(x)的图象在点(2,f(2))处的切线方程为3x?y?11?0，求函数f ( x )的解析式；

（Ⅲ）若x0?5,方程f(x)?8a有三个不同的根，求实数a的取值范围。 解：由题知：f?(x)?3ax2?2bx+c-3a-2b

（Ⅰ）由图可知 函数f ( x )的图像过点( 0 , 3 )，且f??1?= 0

?d?3?d?3

??得?

c?03a?2b?c?3a?2b?0??

（Ⅱ）依题意

f??2?= – 3 且f ( 2 ) = 5

?12a?4b?3a?2b??3

解得a = 1 , b = – 6 ?

8a?4b?6a?4b?3?5?

3

2

所以f ( x ) = x – 6x + 9x + 3

（Ⅲ）依题意 f ( x ) = ax3 + bx2 – ( 3a + 2b )x + 3 ( a＞0 )

2

f??x?= 3ax + 2bx – 3a – 2b

由f??5?= 0?b = – 9a

①

若方程f ( x ) = 8a有三个不同的根，当且仅当 满足f ( 5 )＜8a＜f ( 1 ) ② 由① ② 得 – 25a + 3＜8a＜7a + 3?所以 当

111

111

＜a＜3

＜a＜3时，方程f ( x ) = 8a有三个不同的根。???? 12分

13

x?ax?x?1(a?R)

3

2

4、（根的个数问题）已知函数f(x)?

（1）若函数f(x)在x?x1,x?x2处取得极值，且x1?x2?2，求a的值及f(x)的单调区间； （2）若a?

12

，讨论曲线f(x)与g(x)?

12

x?(2a?1)x?

2

56

(?2?x?1)的交点个数．

解：（1）f'(x)?x2?2ax?1

?x1?x2?2a,x1?x2??

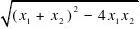
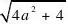
1

?x1?x2???2 ?a?0???????????????????????????2分

22f?(x)?x?2ax?1?x?1

令f?(x)?0得x??1,或x?1

令f?(x)?0得?1?x?1

∴f(x)的单调递增区间为(??,?1)，(1,??)，单调递减区间为(?1,1)????5分

（2）由题f(x)?g(x)得

即1

3x?(a?

1

33313x?ax?x?1?16?0 163212x?(2a?1)x?256 12)x?2ax?1222令?(x)?x?(a?

2)x?2ax?(?2?x?1)????????6分 ???(x)?x?(2a?1)x?2a?(x?2a)(x?1)

令??(x)?0得x?2a或x?1?????????????????7分 ?a?1

2

2a??2a??1

此时，?8a?9

2?0，a?0，有一个交点；??????????9分

1

当2a??2即?1?a?

时，

?2

3a(3?2a)?

9

2

9

2216?0, 916916∴当?8a?当?8a??0即?1?a??时,有一个交点； ?a?0时，有两个交点； ?0，且a?0即?

1

2

9

16 当0?a?综上可知，当a?? 当?9

16时，?8a?或0?a?922?0，有一个交点．?????????13分 1时，有一个交点； ?a?0时，有两个交点．?????????????14分

5、（简单切线问题）已知函数f(x)?

g(x)?f(x)?3bx

2xa32图象上斜率为3的两条切线间的距离为25，函数a

（Ⅰ） 若函数g(x)在x?1处有极值，求g(x)的解析式； ?3． （Ⅱ） 若函数g(x)在区间[?1,1]上为增函数，且b2?mb?4?g(x)在区间[?1,1]上都成立，求实数m的取值范围．