不等式的证明规律及重要公式总结
不等式的证明及重要公式总结
几个常应用的不等式
1、
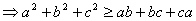
2、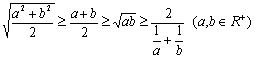
3、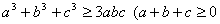 )
)
4、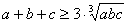 ,
,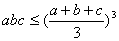 ;
;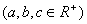
5、 ,
,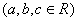
6、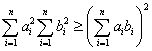 (柯西不等式)
(柯西不等式)
证明方法
法一:作差:
例一: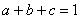 ,求证:
,求证: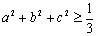 。
。
证:左-右=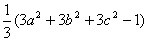
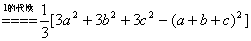
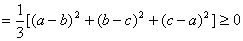
法二:作商;设a、b、c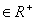 ,且
,且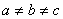 ,求证:
,求证: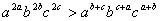
证: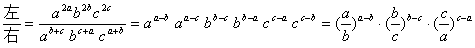
当a>b>0时
当0<a<b时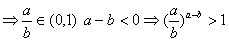
∴ 不论a>b还是a<b,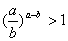 ,同理可证,
,同理可证,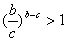 ,
,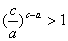 ,……
,……
法三:公式法:例二:a>0,b>0,且a+b=1,求证:
①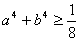 ②
②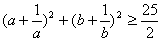
证①由公式: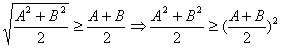 得:
得:
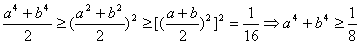
证②由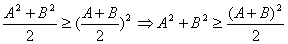
∴ 左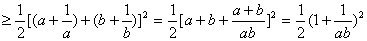 (*)
(*)
∵ 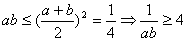
∴ (*)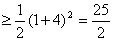
第二篇:不等式的证明方法
不等式的证明方法
【摘要】不等式是数学中的重要工具,不等式的证明方法比较多,本文给出了不等式的常规证法,同时结合导数与积分知识给出两种证明不等式的方法。
【关键词】不等式证明;常用证明方法;函数单调性;定积分
不等式是高中数学的重要组成部分,也是数学中的一个重要工具,而不等式的证明是高中数学中难点之一。由于其题型广泛,涉及面广,技巧性强,证法灵活,本文通过一些例子,归纳整理了一些证明不等式时的常用方法和技巧,并且结合高等数学知识,来证明一些比较困难的不等式,使之过程更加简洁、易懂。
一、初等数学中常用来证明不等式的方法
1.比较法。这是一种证明不等式的最基本的方法,具体有“作差法”和“作商法”两种。此法体现了化归的思想方法,其基本证明思想是把难以比较的式子变成其差与0比较大小,或者其商与1比较大小。一般情况下,若求证的不等式两端是分式时,常用作差法;若求证的不等式两端是乘积形式或幂指数形式时,常用作商法来比较。
2.综合法。由已知条件出发,借助某些已经证明过的不等式和不等式的性质及其有关定力,经过逐步的逻辑推理,到处所要证明的不等式成立。此法的特点是“由因导果”,即从“已知”看“已知”,逐步推向“未知”。
3.分析法。从结论出发,寻找命题成立的充分条件,知道这个条件是可以证明或已经证明的不等式,或者是已经成立的结论,由此便可推到出原不等式成立。此法的特点是“执果索因”,常用的形式是“欲证…,只需证…”。
4.换元法。这是一种使许多实际问题解决中祈祷化难为易,化繁为简作用的方法,有些问题直接证明较为困难,若通过换元的方法去解则很方便,常用于条件不等式的证明,常见的是“三角换元法”和“比值换元法”。
①三角换元法:这是一种常用的换元方法,在解决代数问题时,使用适当的三角函数进行换元,把代数问题转化为三角问题,再充分利用三角函数的性质去解决问题,常见的有如下几种形式: 则令则令则令②比值换元法:此法对于在已知条件中含有许多个等比式的问题,通常可先设一个辅助未知数表示这个比值,然后代入要求证的式子即可。
5.放缩法。这种方法是在证明不等式时,把不等式一边适当放大或缩小,利用不等式的传递性来证明不等式。此法是证明不等式的重要方法,技巧性强。一般用到的技巧有:①舍去一些正项或负项。②在和或积中换大或换小某些项。③扩大或缩小分式的分子或分母等。
6.反证法。某些不等式从正面出发,不容易下手,可以考虑反证法。即先否定结论不成立,然后再依据已知条件及其相关定义、定理、公理等,逐步推导出与这些相矛盾或自相矛盾的结论,从而肯定原有结论是正确的。一般情况下,凡是出现“至少”、“唯一”或者含有否定的命题,适用反证法。此法的步骤为:反设结论找出矛盾肯定结论。
7.数学归纳法。此法一般用来证明与自然数N有关的不等式,在证明过程中需要分两个步骤,这两个缺一不可。
8.判别式法。此法借助于二次函数中,判别式恒小于0,得出二次函数恒大于0,或者恒小于0。
二、高等数学中用来证明不等式的方法
1.利用函数单调性证明。理论依据:若函数在区间内可导,则在内单调递增(或单调递减)的充要条件是(或)。
由于不等式与函数有密切关系,因此,据求证的不等式构造出函数,利用函数的单调性可以证明某些不等式,此方法尤其适用于函数不等式的证明。
例如:证明当时,证明:设,这里,由于,则有,从而在内单调递增,则有,即 ,也即。证毕
2.利用定积分的性质证明不等式。理论依据:设f,g为定义[a,b]在上两个可积函数,若,则有。
定积分是借助于积分学的知识,证明不等式的一种方法,它主要利用积分的基本公式、基本性质、基本定理证明不等式。
例如:已知x>1,求证:。证明:构造函数,取,则,从而由此可得:即: ,证毕.
此题如果要用作差法来证明,困难较大,中间还要用到判别式法等综合知识,具体证明过程如下:
先证明 =
其中,这根据,可得.
因此,对于x>1,则有.
下证
其中,这根据,可得.
因此,对于x>1,则有.
综上所述,结论得到证明。
不等式的证明这类题型,不仅能检验学生的数学基础知识掌握程度,又能衡量学生的数学水平,本文只是粗略的归纳了一些常用方法,通过不断的深入学习,知识的不断积累,相信以后有更多的方法来解决此类问题。
参考文献:
[1]郭大钧.非线性泛函分析(第二版)[M].济南:山东科学技术出版社,20xx.等
-
一元一次不等式总结及练习题
一元一次不等式和一元一次不等式组一.不等关系2.(非负数=大于等于0)=(0和正数=不小于0)(非正数=小于等于0)=(0和负数=…
-
一元一次不等式总结及练习题
第一章一元一次不等式和一元一次不等式组一.不等关系2.(非负数=大于等于0)=(0和正数=不小于0)(非正数=小于等于0)=(0和…
-
一元一次不等式总结与习题训练
一元一次不等式一、不等式的解和解集对于一个含有未知数的不等式,任何一个使这个不等式成立的未知数的值,都叫做这个不等式的解。一个不等…
-
不等式总结
1.不等式的定义:a-b0ab,a-b=0a=b,a-b0ab。?①其实质是运用实数运算来定义两个实数的大小关系。它是本章的基础,…
-
不等式总结
8.一元一次不等式:不等式的左、右两边都是整式,只有一个未知数,并且未知数的最高次数是1,像这样的不等式,叫做一元一次不等式。9.…
-
一元一次不等式总结与习题训练
一元一次不等式一、不等式的解和解集对于一个含有未知数的不等式,任何一个使这个不等式成立的未知数的值,都叫做这个不等式的解。一个不等…
-
一元一次不等式总结及练习题
第一章一元一次不等式和一元一次不等式组一.不等关系2.(非负数=大于等于0)=(0和正数=不小于0)(非正数=小于等于0)=(0和…
-
一元一次不等式总结及练习题
一元一次不等式和一元一次不等式组一.不等关系2.(非负数=大于等于0)=(0和正数=不小于0)(非正数=小于等于0)=(0和负数=…
-
优秀实习生证明
兹有云南师范大学数学学院20xx级唐佳纳同学,于20xx年x月x日至20xx年x月x日在云南省普洱市墨江县联珠镇第三中学七年级组进…
-
归纳猜想证明
归纳—猜想—证明上海市风华中学王晓虹一、教材分析归纳法是由一系列有限的特殊事例得出一般结论的推理方法。归纳法分为不完全归纳法与完全…