求函数极限的若干方法及其应用
求函数极限的若干方法及其应用
1.定义法
2.利用极限四则运算法则
3.利用夹挤性定理求极限
4.利用两个重要极限求极限
5.利迫敛性来求极限
6.用洛必达法则求极限
7.利用定积分求极限
8.利用无穷小量的性质和无穷小量和无穷大量之间的关系求极限
9.利用变量替换求极限
10.利用递推公式计算或证明序列求极限
11.利用等价无穷小量代换来求极限
12.利用函数的连续性求极限
13.利用泰勒公式求极限
14.利用两个准则求极限
15.利用级数收敛的必要条件求极限
16.利用单侧极限求极限
总结
参考文献
外文摘要
目录
1 引言
函数极限的定义及作用
函数极限的计算及多种求法
2 3.1利用左、右极限求极限
2 3.2 利用极限运算法则求极限 3 3.3 利用初等变形求函数极限
3.3.1 约分法
3.3.2 有理化法
3.3.3比较最高次幂法
3.4 利用迫敛性求函数极限
3.5 利用两个重要极限公式求函数极限
3.6 利用变量替换求函数极限
3.6.1利用等价无穷小量替换来求极限
3.6.2 利用其他替换来求极限
3.7 利用无穷小量的性质求函数极限
3.8 利用初等函数的连续性质求函数极限
3.9利用导数的定义求函数极限
3.10 利用洛必达法则求函数极限
3.10.1 00型不定式极限
3.10.2 型不定式极限
3.10.3 其它类型不定式极限
3.11幂指函数求函数极限
3.11.1 )(xf,)(xg的极限均为有限常数,即BA型的极限求法
3.11.2 型未定式极限问题
3.11.3 3.12利用泰勒公式求函数极限
3.11.4 3.13 利用中值定理求函数极限
3.11.5 参考文献
第二篇:求极限的方法总结
求数列极限的方法总结
摘 要 数列极限的求法一直是数列中一个比较重要的问题,本文通过归纳和总结,从不同的方面罗列了它的几种求法。
关键词 数列极限、定义、泰勒公式、无穷小量
极限一直是数学分析中的一个重点内容,而对数列极限的求法可谓是多种多样,通过归纳和总结,我们罗列出一些常用的求法。求数列极限的最基本的方法还是利用数列极限的定义,也要注意运用两个重要极限,其中,可以利用等量代换,展开、约分,三角代换等方法化成比较好求的数列,也可以利用数列极限的四则运算法则计算。夹逼性定理和单调有界原理是很重要的定理,在求的时候要重点注意运用。泰勒公式、洛必达法则、黎曼引理是针对某些特殊的数列而言的。还有一些比较常用的方法,在本文中都一一列举了。
1.定义法
利用数列极限的定义求出数列的极限.设﹛Xn﹜是一个数列,a是实数,如果对任意给定的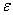 〉0,总存在一个正整数N,当n〉N时,都有
〉0,总存在一个正整数N,当n〉N时,都有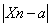 <
<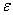 ,我们就称a是数列{Xn}的极限.记为
,我们就称a是数列{Xn}的极限.记为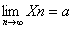 .
.
例1: 按定义证明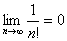 .
.
解:1/n!=1/n(n-1)(n-2)…1≤1/n
令1/n<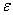 ,则让n>
,则让n>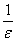 即可,
即可,
存在N=[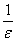 ],当n>N时,不等式:1/n!=1/n(n-1)(n-2)…1≤1/n<
],当n>N时,不等式:1/n!=1/n(n-1)(n-2)…1≤1/n<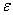 成立,
成立,
所以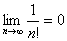 .
.
2.利用极限四则运算法则
对和、差、积、商形式的函数求极限,自然会想到极限四则运算法则.
例2: 求 ,其中
,其中 .
.
解: 分子分母均为无穷多项的和,应分别求和,再用四则运算法则求极限
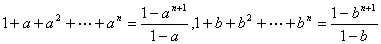 ,
,
原式=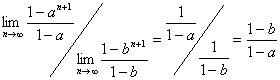 ,
,
3. 利用夹逼性定理求极限
若存在正整数N,当n>N时,有Xn≤Yn≤Zn,且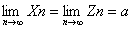 ,则有
,则有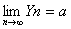 .
.
例3:求{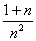 }的极限.
}的极限.
解: 对任意正整数n,显然有
 ,
,
而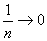 ,
, ,由夹逼性定理得
,由夹逼性定理得
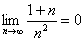 .
.
4.换元法
通过换元将复杂的极限化为简单.
例4.求极限 ,此时
,此时
解:若 有
有 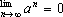 ,令
,令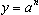 则
则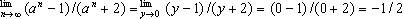
5.单调有界原理
例5.证明数列 有极限,并求其极限。
有极限,并求其极限。
证: 令  ,易知{
,易知{ }递增,且
}递增,且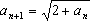
我们用归纳法证明  ≤2. 显然
≤2. 显然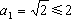 。
。
若 ≤2 则
≤2 则 。
。
故由单调有界原理{ }收敛,设
}收敛,设 →
→ ,则在
,则在 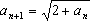 中两边取极限得
中两边取极限得 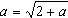 即
即 
解之得  =2 或
=2 或  =-1 明显不合要求,舍去,
=-1 明显不合要求,舍去,
从而 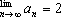
6.先用数学归纳法,再求极限.
例6:求极限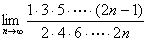
解: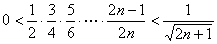
S=
设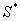 =
= 则有S<
则有S<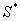
S2=S*S<S*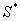 =
=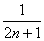
而 ,
,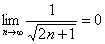 再由夹逼性定理,得
再由夹逼性定理,得
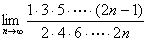 =0
=0
7.利用两个重要极限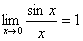 ,
,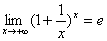 .
.
例7:求
解: 原式=
8.利用等价无穷小来求极限
将数列化成自己熟悉的等价无穷小的形式然后求极限.
例8:求
解:当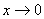 的时候,
的时候, ,
, .
.
而此时, ,所以
,所以
原式=
9.用洛必达法则求极限.适用于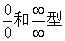
例9:求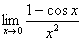
解: 是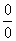 待定型.
待定型.
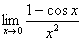 =
=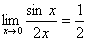
10.积分的定义及性质
例10:求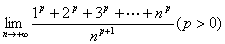
解: 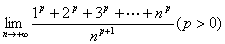 =
=
设 ,则
,则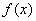 在[0,1]内连续,
在[0,1]内连续,
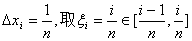
所以, 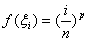
所以原式=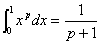
11.级数收敛的必要条件.
设 据必要条件知所求表达式的极限为0.
据必要条件知所求表达式的极限为0.
例11:求
解:设 ,则
,则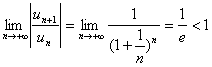
所以该级数收敛,所以 =0
=0
12.对表达式进行展开、合并、约分和因式分解以及分子分母有理化,三角函数的恒等变形。
例12. 求
解:
法一:原式=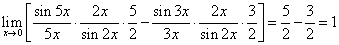
法二:原式=
13.奇数列和偶数列的极限相同,则数列的极限就是这个极限。
例13:求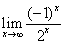 的值
的值
解:奇数列为 =0
=0
偶数列为 =0
=0
所以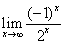 =0
=0
14.利于泰勒展开式求极限。
例14.求
解:原式=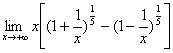 (令t=
(令t= )
)
=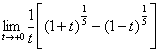 =
= =
=
15.利于无穷小量的性质和无穷小量和无穷大量之间的关系求极限。
利用无穷小量与有界变量的乘积仍为无穷小量,无穷小量与无穷大量互为倒数的关系,以及有限个无穷小的和仍是无穷小等等。
例15:求 的值
的值
解:因为 是无穷小量,而
是无穷小量,而 是有界变量,所以
是有界变量,所以
 还是无穷小量,即
还是无穷小量,即
 =0
=0
16.利用数列的几何、算术平均值求极限。
数列{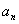 }有极限,则它的几何平均值和算术平均值的极限与与原极限相同。
}有极限,则它的几何平均值和算术平均值的极限与与原极限相同。
例16:求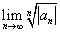 的值
的值
解: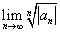 =
= =
=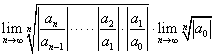
设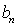 =
= ,因为知
,因为知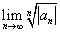 =1
=1
所以,所求原式的极限就等于{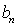 }的极限
}的极限
即原式=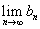 =
=
17.绝对值中的极限
若 ,则
,则
例17:求 的值
的值
解: =
=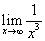 =0
=0
18.利用黎曼引理
例18:求 (a>0)
(a>0)
解:原式=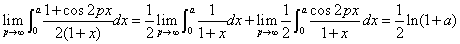
数列极限的方法还有很多,以上给与大致列举。本文在写作过程中得到了****老师多次精心指导,在此表示感谢。
-
归纳函数极限的计算方法
归纳函数极限的计算方法摘要本文总结出了求极限的几种方法比如用定义公式定理性质求极限关键词函数极限计算方法洛必达法则四则运算Thes…
-
求函数极限的方法和技巧
求函作者黄文羊摘要本文就关于求函数极限的方法和技巧作了一个比较全面的概括综合关键词函数极限引言在数学分析与微积分学中极限的概念占有…
-
求函数极限的方法
求函数极限的方法摘要本文主要分两个部分首先归纳和总结出函数极限的定义及其相关的性质其次从不同角度概括出求函数极限的若干主要方法并列…
-
函数极限理论的归纳与解题方法的总结
目录引言1一基本概念与基本理论2一函数极限2二重要极限9三函数的上极限与下极限10四Stolz定理的推广定理11二习题类型与其解题…
-
常用求极限方法的探索与总结
论文题目:————————学院:——————————专业班级:——————————姓名:——————————学号:——————常用…
-
归纳函数极限的计算方法
函数极限的计算方法摘要:本文总结出了求极限的几种方法,比如用定义、公式、定理、性质求极限.关键词:函数极限;计算方法;洛必达法则;…
-
常用求极限方法的探索与总结
论文题目:————————学院:——————————专业班级:——————————姓名:——————————学号:——————常用…
-
求极限的方法 三角函数公式
高数中求极限的16种方法——好东西假如高等数学是棵树木得话,那么极限就是他的根,函数就是他的皮。树没有跟,活不下去,没有皮,只能枯…
-
求数列极限的方法总结
求数列极限的方法总结万学教育海文考研教学与研究中心贺财宝极限是考研数学每年必考的内容在客观题和主观题中都有可能会涉及到平均每年直接…
-
高等数学中求极限的方法小结
宁波大红鹰学院学生数学课程论文高等数学中求极限的方法小结2求极限的常用方法21利用等价无穷小求极限这种方法的理论基础主要包括1有限…
-
公函格式范文
1.概述函,即信函,或称书信。公函,即处理公务所用的书信。公函是党政机关、人民团体、企事业单位间商洽和联系工作时使用的一种文体。公…