归纳函数极限的计算方法
归纳函数极限的计算方法
摘 要 :本文总结出了求极限的几种方法,比如用定义、公式、定理、性质求极限.
关键词:函数极限;计算方法;洛必达法则; 四则运算
The sum of the Method of Computing Function Limit
Abstract:The write sums up in this article several ways of extacting the limit by the means of definition, formula,nature, theorem and so on.
Key Words:Function Limit;Computing method;L’Hospital rules; Four fundamental rules
前言
极限的概念是高等数学中一个最基本、最重要的概念,极限理论是研究连续、导数、积分、级数等的基本工具,因此正确理解和运用极限的概念、掌握极限的求法,对学好数学分析是十分重要的.求极限的方法很多且非常灵活,本文归纳了函数极限计算的一些常见方法和技巧.
1.预备知识
1.1函数极限的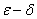 定义
定义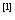
设函数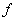 在点
在点 的某个空心邻域
的某个空心邻域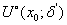 内有定义,
内有定义,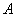 为定数,若对任给的
为定数,若对任给的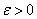 ,存在正数
,存在正数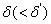 ,使得当
,使得当 时有
时有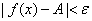 ,则称函数当趋于
,则称函数当趋于 时以
时以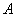 为极限,记作
为极限,记作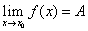 或
或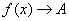
 .
.
2.求函数极限的方法总结
极限是描述函数的变化趋势,以基于图形或直观结合定义可以求出一些简单的函数的极限;但是结构较为复杂的函数的图形不易画出,基于直观也就无法得出极限,本着化繁为简的思想,产生了极限的四则运算法则;由“数列的单调有界准则”和“迫敛准则”产生了两个重要极限和无穷小量的性质—有界函数与无穷小量的积仍是无穷小量;由中值定理得出了罗必达法则.以上也是我们求极限的理论依据,但在个依据下求极限又有各自的技巧.
2.1依据函数极限的迫敛性求极限
函数极限的迫敛性 设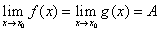 ,且在某
,且在某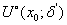 内有
内有 ,则
,则 .
.
例1求极限
解:当 时,有
时,有

而 ,由函数迫敛性可得
,由函数迫敛性可得

同理可得 时,
时, ,即
,即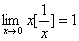
注:依据函数极限的迫敛性求极限时,需判断该函数的上下范围,这时通常用到以下不等式:
2.2 依据极限的四则运算求极限
依据极限的四则运算法则求极限的题目,除了直接使用极限的四则运算法则外,往往还有以下几种类型:
分母极限为0:可先采用“约简分式”或“分子、分母有理化”进行恒等变形,将分母极限化为非零,然后再运用法则:
例2 求极限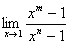 (
( 和
和 都是正整数)
都是正整数)
解:原式=
=
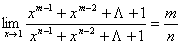
 等未定型:因“
等未定型:因“ ”不是一个数,故该类型的题目不能直接使用运算法则,但可以利用“无穷大量的导数”、“分式有理化”或“通分”等方法,将其转化为极限存在后,再运用法则计算.
”不是一个数,故该类型的题目不能直接使用运算法则,但可以利用“无穷大量的导数”、“分式有理化”或“通分”等方法,将其转化为极限存在后,再运用法则计算.
例3求极限
解:原式=
=
2.3 依据两个重要极限求极限
两个重要的极限: ,
, .
.
函数经过一定变形,若能出现以下情况:

时,也可采用重要极限来求.
例4 求极限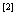
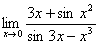
解:原式=
例5 求极限
解:原式=
2.4依据等价无穷小替换求极限
求函数极限,若能恰当采用等价无穷小的代换,可以起到变难为易,化繁为简的作用.需要记住一些常见的等价无穷小, 如当 时:
时:

例6 求极限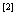
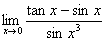
解:原式


注:用等价无穷小替换求极限时,应注意只能用分子、分母整个部分去代换,或是把函数化成积的形式实行无穷小代换,对极限式的相加相减部分不能随意替代.
2.5 依据洛必达法则求极限
洛必达法则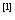 :
:
 型不定式极限 若函数
型不定式极限 若函数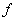 和
和 满足:
满足:
(i) ;
;
(ii)在点 的某空心邻域
的某空心邻域 内两者都可导, 且
内两者都可导, 且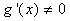
(iii)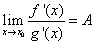 (
(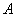 可为实数, 也可为
可为实数, 也可为 或
或 ), 则
), 则

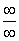 型不定式极限 若函数
型不定式极限 若函数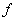 和
和 满足:
满足:
(i) ;
;
(ii)在点 的某右邻域
的某右邻域 内两者都可导, 且
内两者都可导, 且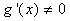
(iii)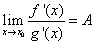 (
(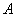 可为实数, 也可为
可为实数, 也可为 或
或 ), 则
), 则

因此函数为 型,通常可采用此法,如下:
型,通常可采用此法,如下:
例7计算极限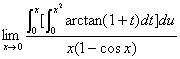
解:原式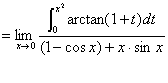


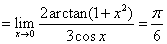
注:“洛必达法则”是求函数极限的有力工具,但在运用中,由于积、商、复合函数的求导会使分子、分母的项数增加, 导致求极限过程繁琐,因此用 法则求
法则求 型的极限是不够的,需综合运用其它方法才能发挥作用.
型的极限是不够的,需综合运用其它方法才能发挥作用.
2.6 依据麦克劳林展开式求极限
一般常见函数的麦克劳林公式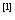 :
:



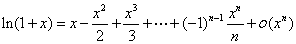


利用洛必达法则求 型极限时,其结果是化成某阶导数的比,而麦克劳林展开式的各项系数正分别含着各阶导数的值,因此对
型极限时,其结果是化成某阶导数的比,而麦克劳林展开式的各项系数正分别含着各阶导数的值,因此对 型函数极限也可采用此法.
型函数极限也可采用此法.
例8 求极限
解:

原式=
注:若本题采用洛必达法则去做,会导致计算过程繁杂.
2.7 运用函数的连续性求极限
函数的连续性定义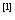 : 设函数
: 设函数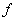 在某
在某 内有定义, 若
内有定义, 若
 ,
,
则称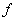 在点
在点 连续.
连续.
若函数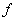 在区间
在区间 上的每一点都连续, 则称
上的每一点都连续, 则称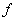 为
为 上的连续函数.
上的连续函数.
例9 计算极限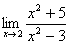
思路: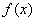 为连续函数,
为连续函数,  为
为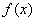 的定义区间上的一点,则
的定义区间上的一点,则 .
.
解:原式=
2.8 运用导数的定义求极限
导数的定义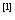 : 设函数
: 设函数 在点
在点 的某邻域内有定义, 若极限
的某邻域内有定义, 若极限

存在, 则称函数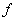 在点
在点 处可导, 并称该极限值为函数
处可导, 并称该极限值为函数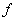 在点
在点 处的导数, 记作
处的导数, 记作 .
.
若函数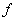 在区间
在区间 上的每一点都可导(对区间端点, 仅考虑相应的单侧导数), 则称
上的每一点都可导(对区间端点, 仅考虑相应的单侧导数), 则称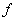 为
为 上的可导函数.
上的可导函数.
例10 计算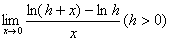
思路:对具有 或
或 形式的极限,可由导数的定义来进行计算.
形式的极限,可由导数的定义来进行计算.
解:原式=
2.9运用定积分的定义求极限
定积分的定义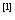 : 设
: 设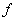 是定义在
是定义在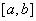 上的一个函数,
上的一个函数,  是一个确定的实数.若对任意给的正数
是一个确定的实数.若对任意给的正数 , 总存在某一正数
, 总存在某一正数 , 使得对
, 使得对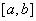 的任何分割
的任何分割 , 以及在其上任意选取的点集
, 以及在其上任意选取的点集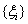 , 只要
, 只要 , 就有
, 就有

则称函数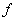 在区间
在区间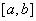 上可积或黎曼可积;数
上可积或黎曼可积;数 称为
称为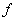 在区间
在区间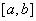 上的定积分或黎曼积分, 记作
上的定积分或黎曼积分, 记作
例11 计算

思路:和式极限,利用定积分定义
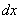 求得极限.
求得极限.
解:原式


2.10 运用微分中值定理求极限
拉格朗日中值定理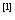 : 若函数
: 若函数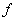 满足如下条件:
满足如下条件:
(i)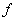 在闭区间
在闭区间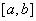 上连续;
上连续;
(ii)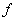 在开区间
在开区间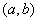 内可导,则在内至少存在一点
内可导,则在内至少存在一点 ,使得
,使得
 .
.
例12:计算

思路:对函数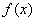 在区间
在区间 上运用拉格朗日中值定理,即可求得.
上运用拉格朗日中值定理,即可求得.
解:原式 (其中
(其中 在
在 区间内)
区间内)
综上所述,求极限时,在不同的函数类型下,所采用的技巧是各不相同的,对同一题也可能有多种求法,有难有易,有时甚至需要结合上述各种方法,才能简单有效的求出,因此学会判断极限的类型和对以上的解法的灵活运用是必要的.
参考文献
[1]华东师范大学数学系. 数学分析(第五版)[M]. 高等教育出版社,2001.
[2]钱志良. 谈极限的求法[J]. 常州信息职业技术学院学报,2003.
[3]李占光. 函数极限的计算方法[J]. 长沙民政职业技术学院学报,2004.
第二篇:极限计算方法总结

毕 业 设 计(论 文)
题 目:极限计算方法总结
(英 文):Conclusion of Calculation Methods
Of Limits
院 别: 计算机科学学院
专 业:数学与应用数学(师范)
姓 名: 陈炜
学 号: 2008034544004
指导教师: 黄术
日 期: 2012年5月
答辩日期: 2012年*月
极限计算方法总结
摘 要
本文归纳了极限的计算方法,对一元函数的极限求法、二元函数的极限求法给出了介绍并举出了例子。由于通项中含有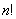 的数列的特殊性,在最后又对其极限的求法给出了归纳。求极限的方法很多,且一题有多种解法,要注意综合运用多种方法,简化计算量。
的数列的特殊性,在最后又对其极限的求法给出了归纳。求极限的方法很多,且一题有多种解法,要注意综合运用多种方法,简化计算量。
关键词:一元函数;二元函数;通项中含有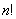 的数列
的数列
Conclusion of Calculation Methods Of Limits
ABSTRACT
This paper summarizes the calculation methods of limits. It not only introduces the methods of the limits of single variable function and binary function, but also gives some examples of them. Because of the specificity of the sequences which contain 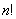 , the paper sums up the methods of the limits of it at the end. Since the calculation of the limits can be solved by different methods, we need to use various methods comprehensively in order to simplify the calculations.
, the paper sums up the methods of the limits of it at the end. Since the calculation of the limits can be solved by different methods, we need to use various methods comprehensively in order to simplify the calculations.
Key words: single variable function;binary function;the sequences which contain 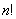
目录
1、一元函数极限计算方法. ...................................................1
1.1、利用极限的定义验证极限的存在. 1
1.2、利用极限四则运算法则. 2
1.3、利用两个重要极限求函数的极限值. 3
1.4、利用夹逼准则求极限. 3
1.5、利用单调有界准则求极限. 4
1.6、利用单侧极限求极限. 5
1.7、利用无穷小的性质求极限和等价无穷小代换求极限. 5
1.8、利用函数的连续性求极限. 7
1.9、利用复合函数求极限. 7
1.10、利用洛必达法则求极限. 8
1.11、利用麦克劳林展开式求极限. 10
1.12、利用定积分定义及性质求极限. 11
1.13、利用级数收敛的必要条件求极限. 12
1.14、利用拉格朗日中值定理求极限. 13
1.15、利用积分中值定理求极限. 14
1.16、利用导数的定义求极限. 15
2、二元函数极限计算方法. ..................................................16
2.1、利用二元函数极限的定义求解. 16
2.2、利用函数的连续性来计算. 16
2.3、利用极限的四则运算法则. 17
2.4、利用夹逼准则求极限. 17
2.5、利用等价无穷小代换求极限. 18
2.6、利用无穷小量乘以有界量仍为无穷小量. 18
2.7、利用复合函数求极限. 19
2.8、利用累次极限求极限. 19
2.9、利用两个重要极限求解. 20
2.10、利用变量代换法求极限. 21
2.11、利用极坐标求极限. 21
2.12、利用恒等变形求极限. 22
2.13、利用二元函数的洛必达法则求极限. 22
3、通项中含有 的数列极限的求法. .........................................23
的数列极限的求法. .........................................23
3.1、利用定积分求通项中含有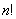 的数列极限. 23
的数列极限. 23
3.2、利用幂级数求通项中含有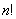 的数列极限. 24
的数列极限. 24
3.3、利用 公式计算通项中含有
公式计算通项中含有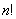 的数列极限. 24
的数列极限. 24
3.4、利用夹逼准则计算通项中含有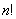 的数列极限. 25
的数列极限. 25
3.5、利用 定理计算通项中含有
定理计算通项中含有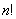 的数列极限. 25
的数列极限. 25
3.6、利用裂差法求通项中含有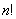 的数列极限. 26
的数列极限. 26
参考文献. .................................................................28
致 谢. ...................................................................29
引言
极限是高等数学中的一个重要内容,前人对极限的求法已经有所研究,因此有
必要总结一下极限的求法,其求法可总结如下:
1、一元函数极限计算方法
1.1、利用极限的定义验证极限的存在
函数极限的 定义:设函数
定义:设函数 在点
在点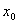 的某个空心邻域
的某个空心邻域 内有定义,
内有定义, 为定数.若对任给的
为定数.若对任给的 ,存在正数
,存在正数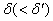 ,使得当
,使得当 时有
时有
 ,
,
则称函数 当
当 时以
时以 为极限,记作
为极限,记作 .
.
极限定义并未给出求极限的具体方法,但却可以验证极限的存在,而且它是研究理论问题的基本方法,用极限定义验证极限存在,一般需经过变形放大,由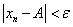 或
或 去寻找满足条件的充分大的正整数
去寻找满足条件的充分大的正整数 或充分小的正数
或充分小的正数 或充分小的正数
或充分小的正数 .
.
例1、证明 .
.
证:对 ,要使
,要使 ,只要
,只要 .因为
.因为 ,不妨设
,不妨设 ,此时
,此时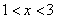 ,从而
,从而 ,
,
因此, =
=
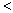
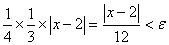 ,
,
 ,则当
,则当 时,总有
时,总有
 ,从而
,从而 .
.
1.2、利用极限四则运算法则
极限的四则运算法则 设 与
与 都存在,则
都存在,则

 ;
;
 ;
;
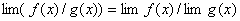 .
.
对和、差、积、商形式的数列求极限,自然会想到极限四则运算法则本身很简单, 但为了能够使用这些法则,往往需要先对函数做某些恒等变形或化简.采用怎样的变形和化简,要根据具体的算式确定,常用的变形或化简有分式的约分或通分、分式的分解、分子或分母的有理化、三角函数的恒等变形、某些求和或求积公式以及适当的变量替换.
例2、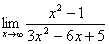 .
.
解: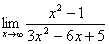 =
= =
= .
.
例3、求极限 .
.
解: =
=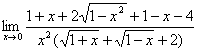
=
=
= .
.
例4、求极限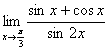 .
.
解: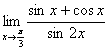 =
= .
.
例5、求极限 .
.
解: =
=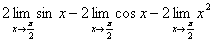
= .
.
1.3、利用两个重要极限求函数的极限值
两个重要极限为: 使用它们求极限时,最重要的是对所给的函数或数列做适当的变形,使之具有相应的形式,有时也可通过变量替换使问题简化.
使用它们求极限时,最重要的是对所给的函数或数列做适当的变形,使之具有相应的形式,有时也可通过变量替换使问题简化.
例6、求下列函数的极限:

 ;
;
 ;
;

 ;
;
 .
.
解:

 .
.

 =
= .
.

 =
= .
.

 =
= .
.
1.4、利用夹逼准则求极限
夹逼准则:
 数列极限的夹逼准则
数列极限的夹逼准则
数列 满足:
满足:

 ,
, ,有
,有 ;
;
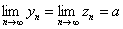 ,则
,则 .
.
 函数极限的夹逼准则
函数极限的夹逼准则
设 ,且当
,且当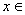
 内
内 时,有
时,有
 ,则
,则
 .
.
注:若把条件中的去心邻域 改为
改为 或
或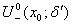 ,则我们可以得到关于单侧极限的夹逼准则.
,则我们可以得到关于单侧极限的夹逼准则.
例7、计算 的极限.
的极限.
解:令

 ,
,
则 ,
,
即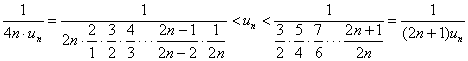 ,
,

又由 ,
,
由夹逼准则可得, .
.
例8、求极限 .
.
解:令 ,
,
因为在实数 上,
上, ,所以,当
,所以,当 时,有
时,有 .
.
因为 ,
, ,
,
故由夹逼准则可得 .
.
1.5、利用单调有界准则求极限
单调有界准则 单调有界数列必有极限,且极限唯一.
首先常用数学归纳法讨论数列的单调性和有界性,再求解方程,可求出极限.
例9、证明数列 收敛,并求其极限.
收敛,并求其极限.
解:证:记
 ,易见数列
,易见数列 是递增的.现在用数学归纳法
是递增的.现在用数学归纳法
证明 有上界.
有上界.
显然 ,假设
,假设 ,则有
,则有 ,从而对一切
,从而对一切 都有
都有 ,
, .
.
由单调有界定理可知,数列 有极限,记为
有极限,记为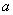 .由于
.由于 ,两边取极限,可得
,两边取极限,可得  ,即有
,即有 ,解得
,解得 .由于数列极限的保不等式性,知道
.由于数列极限的保不等式性,知道 .
.
1.6、利用单侧极限求极限
这种方法使用于求分段函数在分段点处的极限,首先必须考虑分段点的左、右极限,如果左、右极限都存在且相等,则函数在分界点处的极限存在,否则极限不存在.
例10、
求 在
在 =0的极限.
=0的极限.
解:因为 ,
,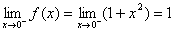 ,
,
故 ,
,
所以 .
.
1.7、利用无穷小的性质求极限和等价无穷小代换求极限
常用到的无穷小的性质有:有限个无穷小的代数和是无穷小;有限个无穷小的积是无穷小;有界函数与无穷小乘积仍是无穷小.
利用等价无穷小替换求极限常常行之有效.常用的几个等价无穷小有:当 时,有
时,有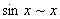 ;
; ;
; ;
; ;
; ;
; ;
; ;
; .
.
例11、求 .
.
解:因为 ,
,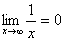 ,
,
所以 .
.
例12、 .
.
解: =
=
 .
.
例13、求极限 .
.
解:因为当 ,
, ,则
,则 .
.
例14、求极限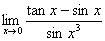 .
.
解:由于 ,且
,且
当 时,有
时,有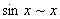 ,
, ,
, ,
,
故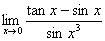 =
=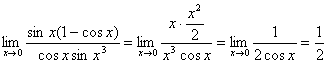 .
.
注:在利用等价无穷小代换求极限时,应注意:只有对所求极限式中相乘或相除的因式才能用等价无穷小量来替换,而对极限式中的相加或相减部分则不能随意替代.如在例14中,若因有
当 时,
时, ,
,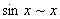 ,而推出
,而推出
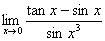 =
= ,则得到的是错误的结果.
,则得到的是错误的结果.
定理1: 设
设 在
在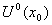 内有定义且不等于
内有定义且不等于 .若
.若 为
为 时的无穷小量,则
时的无穷小量,则 为
为 时的无穷大量.
时的无穷大量.
 若
若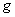 为
为 时的无穷大量,则
时的无穷大量,则 为
为 时的无穷小量.
时的无穷小量.
根据这个定理,对无穷大量的研究可归结为对无穷小量的讨论.
例15、求极限 .
.
解: =
= ,
,
因为 ,所以
,所以 .
.
故 .
.
1.8、利用函数的连续性求极限
若 在点
在点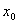 连续,则
连续,则 .
.
特别地,对于基本初等函数有如下定理:
定理2:一切基本初等函数都是其定义域上的连续函数.
由于任何初等函数都是由基本初等函数经过有限次四则运算与复合运算所得到的,所以有
定理3:任何初等函数都是在其定义区间上的连续函数.
例16、 .
.
解:令 ,由于
,由于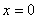 属于初等函数
属于初等函数 的定义区间之内,由初等函数的连续性可知,
的定义区间之内,由初等函数的连续性可知, 在点
在点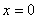 处连续,故有
处连续,故有 =
=
 =
= .
.
1.9、利用复合函数求极限
定理4:若函数 在点
在点 连续,
连续,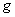 在点
在点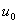 连续,
连续,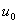 =
= ,则复合函数
,则复合函数 在点
在点 连续.
连续.
根据连续性的定义,上述定理的结论可表示为
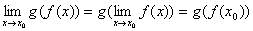 .
.
例17、求 .
.
解:令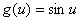 ,
, ,
,
因为 为基本初等函数,故
为基本初等函数,故 在实数
在实数 上连续,
上连续,
又因为 为初等函数,故
为初等函数,故 在实数
在实数 上连续.
上连续.
故 =
=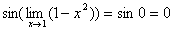 .
.
1.10、利用洛必达法则求极限
洛必达法则:设函数 满足条件:
满足条件:

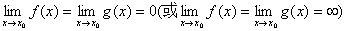 ;
;
 在点
在点 的某邻域内(点
的某邻域内(点 可除外),
可除外), ;
;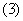
 存在(或为
存在(或为 );
);
那么
 .(当
.(当 改为
改为 时,该定理仍成立.)
时,该定理仍成立.)
例18、求下列函数的极限:
 ;
;
 .
.
解:
 =
=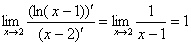 .
.

 =
= =
= =
= =
= =
=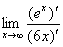 =
=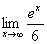 =
= .
.
注:洛必达法则是一种适用于不定式求极限的方法,常见的不定式极限有 型或
型或 型,其他不定式极限必须先化成这两种类型之一,然后再应用洛必达法则.在求解极限时,不能对任何比式极限都按洛必达法则求解,首先必须注意它是不是不定式极限,其次是否满足洛必达法则的其他条件.洛必达法则只说明当
型,其他不定式极限必须先化成这两种类型之一,然后再应用洛必达法则.在求解极限时,不能对任何比式极限都按洛必达法则求解,首先必须注意它是不是不定式极限,其次是否满足洛必达法则的其他条件.洛必达法则只说明当  等于
等于 时,那么
时,那么 也存在且等于
也存在且等于 . 如果
. 如果 不存在时,并不能断定
不存在时,并不能断定 也不存在,只是这是不能用洛必达法则,而须用其他方法讨论
也不存在,只是这是不能用洛必达法则,而须用其他方法讨论 .
.
例19、求 .
.
解:
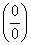
=
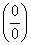
=
= .
.
注: 不是不定式不能用洛必达法则,若对最后一步用洛必达法则,则得到错误的结果1.
不是不定式不能用洛必达法则,若对最后一步用洛必达法则,则得到错误的结果1.
例20、求极限 .
.
虽然是 型,但若不顾条件随便使用洛必达法则,则有
型,但若不顾条件随便使用洛必达法则,则有
 =
= ,就会因右式的极限不存在而推出原极限不存在的错误结论.正确解法如下:
,就会因右式的极限不存在而推出原极限不存在的错误结论.正确解法如下:
解:因为,在实数 上,有
上,有 ,当
,当 时,有
时,有 .
.
故 ,所以
,所以 =
= =1.
=1.
例21、求 .
.
虽然是 型,但若使用洛必达法则,则有
型,但若使用洛必达法则,则有
 =
= =
= ,陷入一个死循环.正确解法应为:
,陷入一个死循环.正确解法应为:
解:
=
=
=1.
1.11、利用麦克劳林展开式求极限
设函数 在
在 的某个邻域内有定义,且
的某个邻域内有定义,且 存在,则对该邻域内任意点
存在,则对该邻域内任意点 ,有
,有 .此式称为
.此式称为 的具有皮亚诺余项的
的具有皮亚诺余项的 阶麦克劳林展式,对某些较复杂的求极限问题,可利用麦克劳林展式加以解决.常用的麦克劳林公式有:
阶麦克劳林展式,对某些较复杂的求极限问题,可利用麦克劳林展式加以解决.常用的麦克劳林公式有:
 ;
;
 ;
;
 ;
;
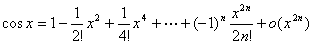 ;
;
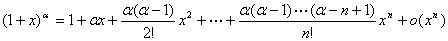 ;
;
 .
.
例22、计算 .
.
解:

 ,
,
所以 =
=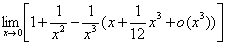
= =
=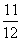 .
.
1.12、利用定积分定义及性质求极限
定积分定义
设 是定义在
是定义在 上的有界函数,用点
上的有界函数,用点
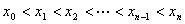
 将
将
区间 任意分割成
任意分割成 个子区间
个子区间
 ,这些子区间及其长度均记作
,这些子区间及其长度均记作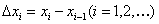 .这些分点或这些闭子区间构成对
.这些分点或这些闭子区间构成对 的一个分割,记为
的一个分割,记为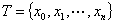 .在每一个区间
.在每一个区间 上任取
上任取 ,作
,作 的和式:
的和式: ,如果当最大子区间的长度
,如果当最大子区间的长度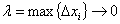 ,和式
,和式 的极限存在,并且其极限值与
的极限存在,并且其极限值与 的分割法以及
的分割法以及 的取法无关,则该极限称为函数
的取法无关,则该极限称为函数 在区间
在区间 上的定积分,记作
上的定积分,记作 .
.
特别地,我们选取某种特殊的分割 ,这里取等分分割:
,这里取等分分割:
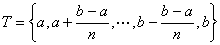 ,则有
,则有
 .
.
若
 取
取
则得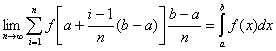 ,
,
取 ,
,
则得 .
.

 ,
,
取 ;
;
取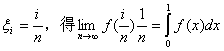 .
.
例23、计算 .
.
解: =
= ,此和式为函数
,此和式为函数 在
在 的特殊积分和,它是把
的特殊积分和,它是把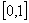
 等分,
等分, 取为
取为 的右端点(即
的右端点(即 )构成的积分和.因为
)构成的积分和.因为 在
在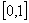 可积,由定积分的定义,有
可积,由定积分的定义,有
 =
= .
.
1.13、利用级数收敛的必要条件求极限
级数收敛的必要条件是: .
.
故对某些极限 可将函数
可将函数 作为级数
作为级数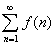 的一般项,只需证明此级数收敛,便有
的一般项,只需证明此级数收敛,便有 .
.
例24、计算 .
.
解: 考虑级数 ,由比值审敛法,得
,由比值审敛法,得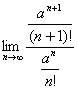 =
= =
=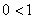 ,所以级数
,所以级数 收敛,由级数收敛的必要条件,得
收敛,由级数收敛的必要条件,得 =0.
=0.
1.14、利用拉格朗日中值定理求极限
拉格朗日中值定理:若函数满足下列条件:
 在闭区间
在闭区间 连续;
连续;
 在开区间
在开区间 可导;
可导;
则在开区间 内至少存在一点
内至少存在一点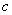 ,使
,使 .
.
拉格朗日公式还有下面几种等价的表示形式:
 ;
; 
 ;
; 
 .
. 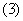
值得注意的是,拉格朗日公式无论对于 ,还是
,还是 都成立,而
都成立,而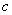 则是介于
则是介于
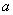 与
与 之间的某一定数.而
之间的某一定数.而 与
与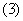 两式的特点,在于把中值点
两式的特点,在于把中值点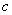 表示成了
表示成了 ,使得不论
,使得不论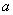 ,
, 为何值,
为何值, 总可为小于1的某一正数.
总可为小于1的某一正数.
例25、计算 .
.
解:令 ,因为
,因为 是基本初等函数,所以
是基本初等函数,所以 在
在 上连续且可导.
上连续且可导.
对它应用拉格朗日中值定理得
 ,
,
即  .
.
又因为 连续,所以
连续,所以 ,从而有
,从而有 =1.
=1.
1.15、利用积分中值定理求极限
积分中值定理:设函数 在闭区间
在闭区间 上连续;
上连续; 在
在 上不变号且可积,则在
上不变号且可积,则在 上至少有一点
上至少有一点 使得
使得 .
.
例26、求 .
.
解: 
=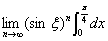

= ,
,
因为 ,所以
,所以 ,
,
又因为 ,
, ,
,
故由夹逼准则,知 =
= .
.
故 =
= =0.
=0.
例27、求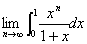 .
.
解: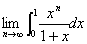
=

=
= .
.
1.16、利用导数的定义求极限
 在点
在点 的导数为
的导数为 .
.
例28、计算 .
.
解:由导数的定义有: =
= .
.
以上所介绍的都是上述介绍了求解极限的基本方法,然而,每一道题目并非只有一种方法.因此在解题中要注意各种方法的综合运用的技巧,使得计算大为简化.以下几道例题都是综合运用了几种方法.
例29、求 .
.
解:
 =
=
 =
= .
.
此法采用洛必达法则配合使用两个重要极限.

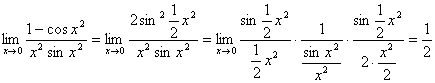 .
.
此法使用三角函数二倍角的余弦公式,配合使用两个重要极限.
 .
.
此法使用了两个重要极限法配合使用无穷小等价代换法以及洛必达法则.
 .
.
此方法使用了无穷小等价代换法配合使用两个重要极限.
 .
.
此方法使用了三角函数二倍角的余弦公式,配合使用无穷小等价代换法.
2、二元函数极限计算方法
二元函数极限的定义跟一元函数表面很类似,但是本质上却发生了质的变化.二元函数在多元函数微积分学中有着重要作用,探讨它的求法是进一步学习多元函数微积分有关概念和方法的基础.下面介绍二元函数的极限求法:
2.1、利用二元函数极限的定义求解
设 为定义在
为定义在 上的二元函数,
上的二元函数, 为
为 的一个聚点,
的一个聚点, 是一个确定的实数.若对任给的正数
是一个确定的实数.若对任给的正数 ,总存在正数
,总存在正数 ,使得当
,使得当 内的点
内的点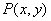 满足
满足 且
且 时,都有
时,都有 ,则
,则 .
.
例1、求 .
.
解:当 时,有
时,有
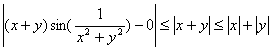 ,
,
对于任意给定的正数 ,取
,取
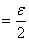 ,则当
,则当 且
且 时,有
时,有 .
.
故由极限定义知 =0.
=0.
2.2、利用函数的连续性来计算
设二元函数 于点
于点 连续,则
连续,则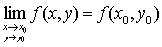 .
.
例2、求 (
( .
.
解:由于 ,
,
故 =
= .
.
2.3、利用极限的四则运算法则
若 ,
,
则  ;
;
 ;
;
 .
.
例3、 .
.
解: =
=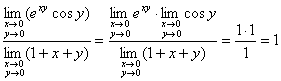 .
.
2.4、利用夹逼准则求极限
若在点
 ,
,
则  .
.
例4、求 .
.
解:因为在 上都有
上都有 ,且
,且
 .
.
由夹逼准则,得 =0.
=0.
2.5、利用等价无穷小代换求极限
利用一元函数中已有的结论对式子进行必要的代换以达到简化的目的,进而求出所要求的极限.在二元函数中常见的等价无穷小有:
当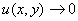 时,有
时,有 ;
; ;
;
 ;
; ;
; ;
;
 ;
; ;
; .
.
例5、求 .
.
解:因为当 时,有
时,有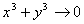 ,有两个重要极限,可知
,有两个重要极限,可知
等价于 ,故对于原式有
,故对于原式有
 .
.
例6、求 .
.
解:当 时,有
时,有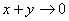 ,故有
,故有 ,则原式有
,则原式有
 =
= .
.
2.6、利用无穷小量乘以有界量仍为无穷小量
若 ,而
,而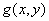 在点
在点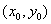 邻域内有界,则
邻域内有界,则
 .
.
例7、计算 .
.
解:因为 ,且
,且 ,
,
故 =0.
=0.
2.7、利用复合函数求极限
若函数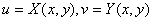 在点
在点 存在极限,并且函数
存在极限,并且函数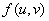 在点
在点 连续,其中
连续,其中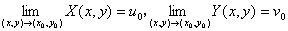 ,则复合函数
,则复合函数
 于点
于点 存在极限,且
存在极限,且
 .
.
例8、计算 .
.
解:令 ,则
,则 .
.
所以 =
= .
.
2.8、利用累次极限求极限
设二重极限 ,且
,且 也存在,则累次极限
也存在,则累次极限 必定存在,且等于
必定存在,且等于 ,即
,即 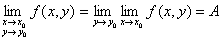 .
.
推论1、如果下面三个极限都存在
 ,
, ,
, ,
,
则两个累次极限 ,
, 都存在,且都等于
都存在,且都等于 .
.
推论2、若累次极限 与
与 都存在,但不相等,则二重极限
都存在,但不相等,则二重极限 一定不存在.
一定不存在.
例9、求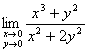 .
.
解: ,
,
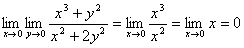 ,
,
因为 ,即两个累次极限不相等,
,即两个累次极限不相等,
所以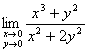 不存在.
不存在.
2.9、利用两个重要极限求解
 ,它们分别是一元函数中两个
,它们分别是一元函数中两个
重要极限的推广,其中当 时,
时,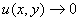 .
.
例10、求极限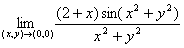 .
.
解: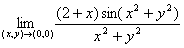
=
= .
.
例11、求极限 .
.
解: =
= ,
,
而 ,
,
所以 =
= =
=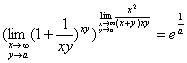 .
.
2.10、利用变量代换法求极限
通过变量代换可以将某些二元函数的极限转化为一元函数的极限来计算,从而使二元函数的极限变得简单.
例12、求极限 .
.
解:令 ,因为
,因为 ,
,
所以当 时,
时,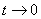 ,则
,则
 =
=



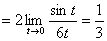 .
.
2.11、利用极坐标求极限
在所求二元函数极限中,若有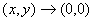 ,且二元函数中含有
,且二元函数中含有 时,可采用极坐标变换法,令
时,可采用极坐标变换法,令 ,将二元函数极限转化为一元函数极限或已知极限来求解.
,将二元函数极限转化为一元函数极限或已知极限来求解.
例13、求 .
.
解:令 ,则原式可化为
,则原式可化为
 =
= .
.
例14、求 .
.
解:令 ,则原式可化为
,则原式可化为
 =
= .
.
2.12、利用恒等变形求极限
将二元函数进行恒等变形,例如分母或分子有理化等,以约去零因子或无穷大因式.
例15、求极限 .
.
解: =
=
 .
.
2.13、利用二元函数的洛必达法则求极限
若二元函数 满足:
满足:

 为有限点;
为有限点;
 ;
;

 ,
, 在点
在点 的某空心邻域内可微,且
的某空心邻域内可微,且 不同时为零;
不同时为零;
 .
.
则 .(条件
.(条件 改为
改为 时结论仍然成立.)
时结论仍然成立.)
例16、求 .
.
解:由二元函数的洛必达法则,可得

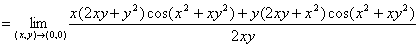
 .
.
以上就是常见的二元函数求极限的方法,希望对读者能够有所帮助.
3、通项中含有 的数列极限的求法
的数列极限的求法
由于数列通项中 的特殊性,需要借助多方面的数学知识,所以有必要来认识一下通项中含有
的特殊性,需要借助多方面的数学知识,所以有必要来认识一下通项中含有 的数列极限的求法.
的数列极限的求法.
3.1、利用定积分求通项中含有 的数列极限
的数列极限
通项中含有 的数列极限,由于
的数列极限,由于 的特殊性,直接求非常困难,而转化为定积分来求解就会相对容易.
的特殊性,直接求非常困难,而转化为定积分来求解就会相对容易.
例1、求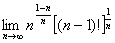 .
.
解: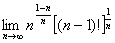 =
= =
=
=
= =
=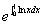 =
= .
.
3.2、利用幂级数求通项中含有 的数列极限
的数列极限
利用简单的初等函数(特别是基本初等函数)的麦克劳林展开式,常能求得一些特殊形式的数列极限.
例2、求 .
.
解:因为
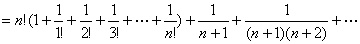 ,
,
记 ,
, ,
,
则 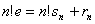 ,
,
易知  ,
,
故由夹逼准则知  1.
1.
所以  =
=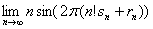 =
=
 .
.
3.3、利用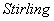 公式计算通项中含有
公式计算通项中含有 的数列极限
的数列极限
 公式:
公式:
 .
.
例3、求 .
.
解:由 公式,可得
公式,可得 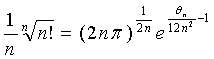 ,
,
因为  ,
,
所以  =
=

= .
.
3.4、利用夹逼准则计算通项中含有 的数列极限
的数列极限
夹逼准则:设数列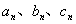 ,
, ,且
,且 ,则有
,则有 .
.
例4、求 .
.
解:记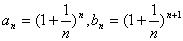 ,则
,则
 ,
, ,
,
对于所有的正整数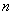 ,都有
,都有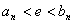 ,从而有
,从而有 ,
,
因为 ,所以有
,所以有 .
.
又因为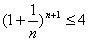 ,所以有
,所以有 .
.
由上面两式,可以得到  ,
,
所以有  ,
,
注意到 ,
,
所以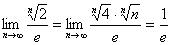 ,
,
故由夹逼准则可知 =1.
=1.
3.5、利用 定理计算通项中含有
定理计算通项中含有 的数列极限
的数列极限
 定理:设数列
定理:设数列 和
和 满足下列条件
满足下列条件
 数列
数列 严格递增且发散到
严格递增且发散到 ;
;
 数列
数列 发散到
发散到 ;
;
则有数列 也收敛,且
也收敛,且 .
.
例5、求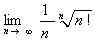 .
.
解:记 ,由
,由 定理,可得
定理,可得

=
 =
= =
= ,
,
所以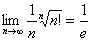 .
.
3.6、利用裂差法求通项中含有 的数列极限
的数列极限
对于数列和式的极限,可通过拆分数列的通项公式,使其和式展开式相邻两项相互抵消,从而简化了极限式子.
例6、求 .
.
解:因为 =
=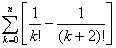
= ,
,
所以 =
=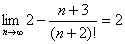 .
.
求通项中含有 数列极限的方法,具有一定的灵活性,上面介绍的是求通项数列中含有
数列极限的方法,具有一定的灵活性,上面介绍的是求通项数列中含有 的数列极限的常用方法,希望能对于我们求解数列极限有所帮助.
的数列极限的常用方法,希望能对于我们求解数列极限有所帮助.
小结:对于求解极限的方法,前人已经有了一定的研究.本文对前人的求解极限的方法做出了较为全面的总结,需要注意的是,极限的计算方法灵活多变,往往一道题目不仅仅只有单一解法,这就要求我们要综合运用多种方法,从而简化计算.事无巨细,本文可能有一些极限的求解方法没有提到,希望读者能给出建议,本人将会虚心接受,完善这篇文章.
参考文献
[1]同济大学数学系.《高等数学》(上册)·第六版[M].高等数学出版社,20##年.
[2]华东师大数学系.《数学分析》(上、下册)[M].高等教育出版社,20##年.
[3]刘玉链,傅沛仁.《数学分析讲义》(上、下册)·第五版[M].高等教育出版社,20##年.
[4]郑晓珍.关于极限的四则运算法则[J].数学教学与研究考试刊,20##年57期.
[5]张明欢.二重极限的计算方法讨论[J].山西煤炭管理干部学院学报,20##年1
月.
[6]张再云,陈湘栋,丁卫平,涂建斌.极限计算的方法与技巧[J].湖南理工学院学
报(自然科学版), 20##年6月第22卷第2期.
[7]李红.中含有 的数列极限的计算通项方法[J].重庆职业技术学院学报,20##年1月第16卷第1期.
的数列极限的计算通项方法[J].重庆职业技术学院学报,20##年1月第16卷第1期.
[8]李国华.函数极限的几种求法[J].高师理科学刊,第31卷.
致 谢
本论文是在我的指导教师黄术老师的亲切关怀和悉心指导下完成的.非常感谢黄老师对我的指导和讲解,在与老师的接触过程中,老师严肃的科学态度,严谨的治学精神,精益求精的工作作风,深深地感染和激励着我.从题目的选择到最终完成,黄术老师都始终给予我细心的指导和不懈的支持,为本人提供了大量宝贵的意见,并且不厌其烦的纠正我在写论文过程中所犯的错误.
同时,感谢大学四年所有老师对我学业的教导和所有同窗在学习、生活上对我的帮助.
最后,感谢我的父母在各方面对我的全力支持和无止尽的关爱,使我一直幸福地学习和生活着.
-
归纳函数极限的计算方法
归纳函数极限的计算方法摘要本文总结出了求极限的几种方法比如用定义公式定理性质求极限关键词函数极限计算方法洛必达法则四则运算Thes…
-
求函数极限的方法和技巧
求函作者黄文羊摘要本文就关于求函数极限的方法和技巧作了一个比较全面的概括综合关键词函数极限引言在数学分析与微积分学中极限的概念占有…
-
求函数极限的方法
求函数极限的方法摘要本文主要分两个部分首先归纳和总结出函数极限的定义及其相关的性质其次从不同角度概括出求函数极限的若干主要方法并列…
-
函数极限理论的归纳与解题方法的总结
目录引言1一基本概念与基本理论2一函数极限2二重要极限9三函数的上极限与下极限10四Stolz定理的推广定理11二习题类型与其解题…
-
常用求极限方法的探索与总结
论文题目:————————学院:——————————专业班级:——————————姓名:——————————学号:——————常用…
-
归纳函数极限的计算方法
函数极限的计算方法摘要:本文总结出了求极限的几种方法,比如用定义、公式、定理、性质求极限.关键词:函数极限;计算方法;洛必达法则;…
-
常用求极限方法的探索与总结
论文题目:————————学院:——————————专业班级:——————————姓名:——————————学号:——————常用…
-
求极限的方法 三角函数公式
高数中求极限的16种方法——好东西假如高等数学是棵树木得话,那么极限就是他的根,函数就是他的皮。树没有跟,活不下去,没有皮,只能枯…
-
求函数极限的若干方法及其应用
求函数极限的若干方法及其应用1.定义法2.利用极限四则运算法则3.利用夹挤性定理求极限4.利用两个重要极限求极限5.利迫敛性来求极…
-
求数列极限的方法总结
求数列极限的方法总结万学教育海文考研教学与研究中心贺财宝极限是考研数学每年必考的内容在客观题和主观题中都有可能会涉及到平均每年直接…