高考数学知识点总结014导数p2
导数 知识要点
1. 导数(导函数的简称)的定义:设 是函数
是函数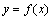 定义域的一点,如果自变量
定义域的一点,如果自变量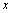 在
在 处有增量
处有增量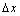 ,则函数值
,则函数值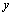 也引起相应的增量
也引起相应的增量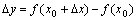 ;比值
;比值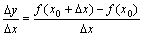 称为函数
称为函数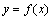 在点
在点 到
到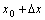 之间的平均变化率;如果极限
之间的平均变化率;如果极限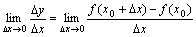 存在,则称函数
存在,则称函数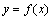 在点
在点 处可导,并把这个极限叫做
处可导,并把这个极限叫做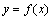 在
在 处的导数,记作
处的导数,记作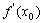 或
或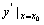 ,即
,即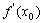 =
=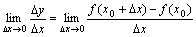 .
.
注:①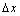 是增量,我们也称为“改变量”,因为
是增量,我们也称为“改变量”,因为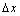 可正,可负,但不为零.
可正,可负,但不为零.
②以知函数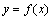 定义域为
定义域为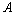 ,
,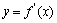 的定义域为
的定义域为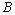 ,则
,则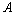 与
与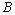 关系为
关系为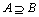 .
.
2. 函数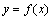 在点
在点 处连续与点
处连续与点 处可导的关系:
处可导的关系:
⑴函数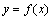 在点
在点 处连续是
处连续是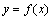 在点
在点 处可导的必要不充分条件.
处可导的必要不充分条件.
可以证明,如果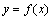 在点
在点 处可导,那么
处可导,那么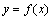 点
点 处连续.事实上,令
处连续.事实上,令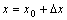 ,则
,则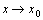 相当于
相当于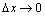 .
.
于是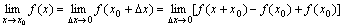
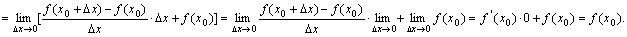 ⑵如果
⑵如果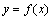 点
点 处连续,那么
处连续,那么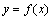 在点
在点 处可导,是不成立的.
处可导,是不成立的.
例: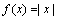 在点
在点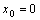 处连续,但在点
处连续,但在点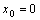 处不可导,因为
处不可导,因为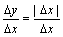 ,当
,当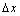 >0时,
>0时,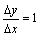 ;当
;当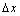 <0时,
<0时,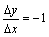 ,故
,故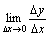 不存在.
不存在.
注:①可导的奇函数函数其导函数为偶函数.②可导的偶函数函数其导函数为奇函数.
3. 导数的几何意义:
函数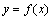 在点
在点 处的导数的几何意义就是曲线
处的导数的几何意义就是曲线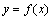 在点
在点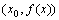 处的切线的斜率,也就是说,曲线
处的切线的斜率,也就是说,曲线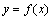 在点P
在点P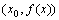 处的切线的斜率是
处的切线的斜率是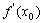 ,切线方程为
,切线方程为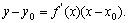
4. 求导数的四则运算法则:
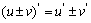
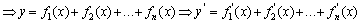
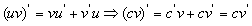 (
(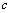 为常数)
为常数) 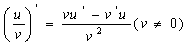
注:①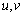 必须是可导函数.②若两个函数可导,则它们和、差、积、商必可导;若两个函数均不可导,则它们的和、差、积、商不一定不可导.
必须是可导函数.②若两个函数可导,则它们和、差、积、商必可导;若两个函数均不可导,则它们的和、差、积、商不一定不可导.
例如:设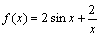 ,
,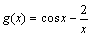 ,则
,则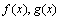 在
在 处均不可导,但它们和
处均不可导,但它们和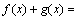
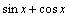 在
在 处均可导.
处均可导.
5. 复合函数的求导法则: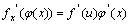 或
或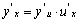 复合函数的求导法则可推广到多个中间变量的情形.
复合函数的求导法则可推广到多个中间变量的情形.
6. 函数单调性:⑴函数单调性的判定方法:设函数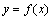 在某个区间内可导,如果
在某个区间内可导,如果 >0,则
>0,则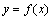 为增函数;如果
为增函数;如果 <0,则
<0,则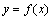 为减函数.
为减函数.
⑵常数的判定方法;如果函数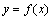 在区间
在区间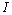 内恒有
内恒有 =0,则
=0,则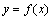 为常数.
为常数.
注:①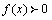 是f(x)递增的充分条件,但不是必要条件,如
是f(x)递增的充分条件,但不是必要条件,如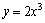 在
在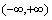 上并不是都有
上并不是都有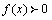 ,有一个点例外即x=0时f(x) = 0,同样
,有一个点例外即x=0时f(x) = 0,同样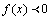 是f(x)递减的充分非必要条件.
是f(x)递减的充分非必要条件.
②一般地,如果f(x)在某区间内有限个点处为零,在其余各点均为正(或负),那么f(x)在该区间上仍旧是单调增加(或单调减少)的.
7. 极值的判别方法:(极值是在 附近所有的点,都有
附近所有的点,都有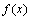 <
< ,则
,则 是函数
是函数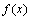 的极大值,极小值同理)
的极大值,极小值同理)
当函数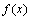 在点
在点 处连续时,
处连续时,
①如果在 附近的左侧
附近的左侧 >0,右侧
>0,右侧 <0,那么
<0,那么 是极大值;
是极大值;
②如果在 附近的左侧
附近的左侧 <0,右侧
<0,右侧 >0,那么
>0,那么 是极小值.
是极小值.
也就是说 是极值点的充分条件是
是极值点的充分条件是 点两侧导数异号,而不是
点两侧导数异号,而不是 =0①. 此外,函数不可导的点也可能是函数的极值点②.当然,极值是一个局部概念,极值点的大小关系是不确定的,即有可能极大值比极小值小(函数在某一点附近的点不同).
=0①. 此外,函数不可导的点也可能是函数的极值点②.当然,极值是一个局部概念,极值点的大小关系是不确定的,即有可能极大值比极小值小(函数在某一点附近的点不同).
注①: 若点 是可导函数
是可导函数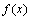 的极值点,则
的极值点,则 =0. 但反过来不一定成立. 对于可导函数,其一点
=0. 但反过来不一定成立. 对于可导函数,其一点 是极值点的必要条件是若函数在该点可导,则导数值为零.
是极值点的必要条件是若函数在该点可导,则导数值为零.
例如:函数 ,
, 使
使 =0,但
=0,但 不是极值点.
不是极值点.
②例如:函数 ,在点
,在点 处不可导,但点
处不可导,但点 是函数的极小值点.
是函数的极小值点.
8. 极值与最值的区别:极值是在局部对函数值进行比较,最值是在整体区间上对函数值进行比较.
注:函数的极值点一定有意义.
9. 几种常见的函数导数:
I. (
(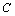 为常数)
为常数) 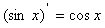
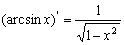
 (
( )
) 

II. 
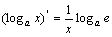

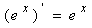

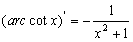
III. 求导的常见方法:
①常用结论: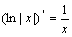 .
.
②形如 或
或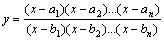 两边同取自然对数,可转化求代数和形式.
两边同取自然对数,可转化求代数和形式.
③无理函数或形如 这类函数,如
这类函数,如 取自然对数之后可变形为
取自然对数之后可变形为 ,对两边求导可得
,对两边求导可得 .
.
第二篇:高考数学知识点总结014导数p2
§14.导数 知识要点
1. 导数(导函数的简称)的定义:设 是函数
是函数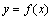 定义域的一点,如果自变量
定义域的一点,如果自变量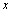 在
在 处有增量
处有增量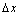 ,则函数值
,则函数值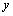 也引起相应的增量
也引起相应的增量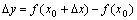 ;比值
;比值 称为函数
称为函数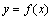 在点
在点 到
到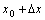 之间的平均变化率;如果极限
之间的平均变化率;如果极限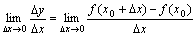 存在,则称函数
存在,则称函数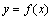 在点
在点 处可导,并把这个极限叫做
处可导,并把这个极限叫做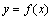 在
在 处的导数,记作
处的导数,记作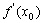 或
或 ,即
,即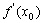 =
=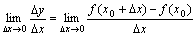 .
.
注:①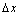 是增量,我们也称为“改变量”,因为
是增量,我们也称为“改变量”,因为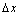 可正,可负,但不为零.
可正,可负,但不为零.
②以知函数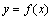 定义域为
定义域为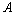 ,
,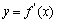 的定义域为
的定义域为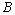 ,则
,则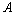 与
与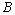 关系为
关系为 .
.
2. 函数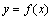 在点
在点 处连续与点
处连续与点 处可导的关系:
处可导的关系:
⑴函数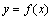 在点
在点 处连续是
处连续是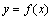 在点
在点 处可导的必要不充分条件.
处可导的必要不充分条件.
可以证明,如果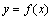 在点
在点 处可导,那么
处可导,那么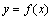 点
点 处连续.事实上,令
处连续.事实上,令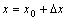 ,则
,则 相当于
相当于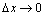 .
.
于是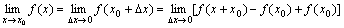
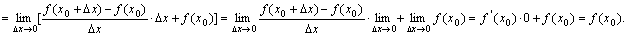 ⑵如果
⑵如果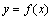 点
点 处连续,那么
处连续,那么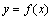 在点
在点 处可导,是不成立的.
处可导,是不成立的.
例: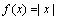 在点
在点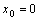 处连续,但在点
处连续,但在点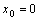 处不可导,因为
处不可导,因为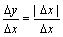 ,当
,当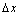 >0时,
>0时,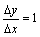 ;当
;当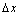 <0时,
<0时, ,故
,故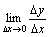 不存在.
不存在.
注:①可导的奇函数函数其导函数为偶函数.②可导的偶函数函数其导函数为奇函数.
3. 导数的几何意义:
函数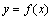 在点
在点 处的导数的几何意义就是曲线
处的导数的几何意义就是曲线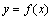 在点
在点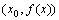 处的切线的斜率,也就是说,曲线
处的切线的斜率,也就是说,曲线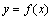 在点P
在点P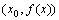 处的切线的斜率是
处的切线的斜率是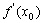 ,切线方程为
,切线方程为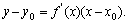
4. 求导数的四则运算法则:
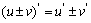
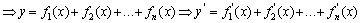
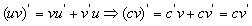 (
(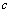 为常数)
为常数) 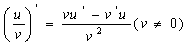
注:①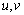 必须是可导函数.②若两个函数可导,则它们和、差、积、商必可导;若两个函数均不可导,则它们的和、差、积、商不一定不可导.
必须是可导函数.②若两个函数可导,则它们和、差、积、商必可导;若两个函数均不可导,则它们的和、差、积、商不一定不可导.
例如:设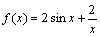 ,
,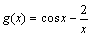 ,则
,则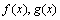 在
在 处均不可导,但它们和
处均不可导,但它们和
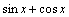 在
在 处均可导.
处均可导.
5. 复合函数的求导法则: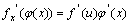 或
或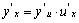 复合函数的求导法则可推广到多个中间变量的情形.
复合函数的求导法则可推广到多个中间变量的情形.
6. 函数单调性:⑴函数单调性的判定方法:设函数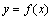 在某个区间内可导,如果
在某个区间内可导,如果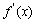 >0,则
>0,则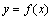 为增函数;如果
为增函数;如果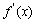 <0,则
<0,则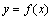 为减函数.
为减函数.
⑵常数的判定方法;如果函数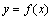 在区间
在区间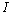 内恒有
内恒有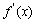 =0,则
=0,则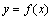 为常数.
为常数.
注:① 是f(x)递增的充分条件,但不是必要条件,如
是f(x)递增的充分条件,但不是必要条件,如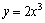 在
在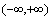 上并不是都有
上并不是都有 ,有一个点例外即x=0时f(x) = 0,同样
,有一个点例外即x=0时f(x) = 0,同样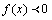 是f(x)递减的充分非必要条件.
是f(x)递减的充分非必要条件.
②一般地,如果f(x)在某区间内有限个点处为零,在其余各点均为正(或负),那么f(x)在该区间上仍旧是单调增加(或单调减少)的.
7. 极值的判别方法:(极值是在 附近所有的点,都有
附近所有的点,都有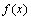 <
<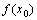 ,则
,则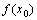 是函数
是函数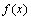 的极大值,极小值同理)
的极大值,极小值同理)
当函数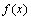 在点
在点 处连续时,
处连续时,
①如果在 附近的左侧
附近的左侧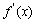 >0,右侧
>0,右侧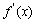 <0,那么
<0,那么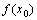 是极大值;
是极大值;
②如果在 附近的左侧
附近的左侧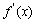 <0,右侧
<0,右侧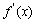 >0,那么
>0,那么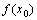 是极小值.
是极小值.
也就是说 是极值点的充分条件是
是极值点的充分条件是 点两侧导数异号,而不是
点两侧导数异号,而不是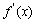 =0①. 此外,函数不可导的点也可能是函数的极值点②.当然,极值是一个局部概念,极值点的大小关系是不确定的,即有可能极大值比极小值小(函数在某一点附近的点不同).
=0①. 此外,函数不可导的点也可能是函数的极值点②.当然,极值是一个局部概念,极值点的大小关系是不确定的,即有可能极大值比极小值小(函数在某一点附近的点不同).
注①: 若点 是可导函数
是可导函数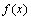 的极值点,则
的极值点,则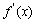 =0. 但反过来不一定成立. 对于可导函数,其一点
=0. 但反过来不一定成立. 对于可导函数,其一点 是极值点的必要条件是若函数在该点可导,则导数值为零.
是极值点的必要条件是若函数在该点可导,则导数值为零.
例如:函数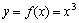 ,
, 使
使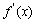 =0,但
=0,但 不是极值点.
不是极值点.
②例如:函数 ,在点
,在点 处不可导,但点
处不可导,但点 是函数的极小值点.
是函数的极小值点.
8. 极值与最值的区别:极值是在局部对函数值进行比较,最值是在整体区间上对函数值进行比较.
注:函数的极值点一定有意义.
9. 几种常见的函数导数:
I. (
(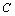 为常数)
为常数) 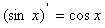

 (
( )
) 

II. 


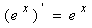

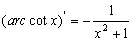
III. 求导的常见方法:
①常用结论: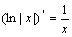 .
.
②形如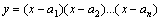 或
或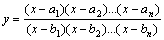 两边同取自然对数,可转化求代数和形式.
两边同取自然对数,可转化求代数和形式.
③无理函数或形如 这类函数,如
这类函数,如 取自然对数之后可变形为
取自然对数之后可变形为 ,对两边求导可得
,对两边求导可得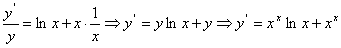 .
.
-
20xx高考数学易错知识点全总结
私立教育网Http20xx高考数学易错知识点全总结集合与简易逻辑易错点1遗忘空集致误错因分析由于空集是任何非空集合的真子集因此对于…
-
20xx年高考数学重点难点总结
20xx年高考数学重点难点总结夯实基础知识形成知识的纵横联系的网络突出主干知识重视思想方法的渗透和运用这些始终是高考的主旋律今年高…
-
20xx年高考数学主要考点总结
20xx年高考数学主要考点总结专题一集合考点1集合的基本运算考点2集合之间的关系专题二函数考点3函数及其表示考点4函数的基本性质考…
-
20xx年高考数学数列知识点总结
导航教育独家经典讲义20xx年高考数列基础知识点和方法归纳二定义与性质1等差数列的定义与性质定义an1andd为常数ana1n1d…
-
20xx年高考数学重点难点总结
20xx年高考数学重点难点总结夯实基础知识形成知识的纵横联系的网络突出主干知识重视思想方法的渗透和运用这些始终是高考的主旋律今年高…
-
高考数学知识点总结
一、集合、简易逻辑(14课时,8个)1.集合;2.子集;3.补集;4.交集;5.并集;6.逻辑连结词;7.四种命题;8.充要条件.…
-
20xx年高考数学知识点总结:三角函数求值考点
三角函数的求值一、教学目标:能正确地运用三角函数的有关公式进行三角函数式的求值.二、教学重点:有关公式的灵活应用及一些常规技巧的运…
-
初一数学知识点总结
初一数学(上)知识点代数初步知识1.代数式:用运算符号+-×÷连接数及字母的式子称为代数式(单独一个数或一个字母也是代数式)2.几…
-
浙教版九年级数学知识点总结
一.反比例函数一.知识框架二.知识概念1.反比例函数:形如y=k(k为常数,k≠0)的函数称为反比例函数。其他形式xy=kxy?k…
-
小学数学知识点总结
一年级上册1、2、3、4、数一数(1~10)比一比(多少、长短、高矮、)1~5的认识和加减法(比大小、第几、几和几、加法、减法、0…