导航教育独家经典讲义

20xx年高考数列基础知识点和方法归纳

二．定义与性质

1. 等差数列的定义与性质

定义：an?1?an?d（d为常数），an?a1??n?1?d 等差中项：x，A，y成等差数列?2A?x?y

前n项和Sn?

?a1?an?n?na

2

1?

n?n?1?

d 2

性质：?an?是等差数列

（1）若m?n?p?q，则am?an?ap?aq；

（2）数列?a2n?1??,a2n??,a2n?1?仍为等差数列，Sn，S2n?Sn，S3n?S2n……仍为等差数列，公差为nd；

（3）若三个成等差数列，可设为a?d，a，a?d （4）若an，bn是等差数列，且前n项和分别为Sn，Tn，则

2

2

amS2m?1

? bmT2m?1

（5）?an?为等差数列?Sn?an?bn（a，b为常数，是关于n的常数项为0的二次函数）

1

导航教育独家经典讲义

或者求出?an?中的正、负分界项， Sn的最值可求二次函数Sn?an2?bn的最值；

即：当a1?0，d?0，解不等式组??an?0可得Sn达到最大值时的n值.

?an?1?0

?an?0当a1?0，d?0，由?可得Sn达到最小值时的n值. a?0?n?1

(6)项数为偶数2n的等差数列?an?，有

S2n?n(a1?a2n)?n(a2?a2n?1)???n(an?an?1)(an,an?1为中间两项) S偶?S奇?nd，S奇

S偶?an. an?1

，有 （7）项数为奇数2n?1的等差数列?an?

S2n?1?(2n?1)an(an为中间项)， S奇?S偶?an，

2. 等比数列的定义与性质 定义：S奇S偶?n. n?1an?1?q（q为常数，q?0），an?a1qn?1 .an

2等比中项：x、G、y成等比数列?G?

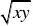
xy，或G? ?na1(q?1)?前n项和：Sn??a1?1?qn?（要注意！） (q?1)??1?q

性质：?an?是等比数列

（1）若m?n?p?q，则am·an?ap·aq

（2）Sn，S2n?Sn，S3n?S2n……仍为等比数列,公比为q. 注意：由Sn求an时应注意什么？

2 n

导航教育独家经典讲义

n?1时，a1?S1；n?2时，an?Sn?Sn?1 .

三．判定与证明

等差数列的判定方法

（1） 定义法：若an?an?1?d或an?1?an?d(常数n?N)? ?an?是等差数列． ?

（2） 等差中项：数列?an?是等差数列?2an?an-1?an?1(n?2)?2an?1?an?an?2．

（3） 数列?an?是等差数列?an?kn?b（其中k,b是常数）。

等差数列的证明方法

定义法：若an?an?1?d或an?1?an?d(常数n?N)? ?an?是等差数列． ?（4） 数列?an?是等差数列?Sn?An2?Bn,（其中A、B是常数）。

等比数列的判定方法

（1）用定义：对任意的n,都有an?1?qan或

数列

（2） 等比中项：an2?an?1an?1（an?1an?1?0）?{an}为等比数列

（3） 通项公式：an?A?Bn?A?B?0??{an}为等比数列

（4）前n项和公式：Sn?A?A?Bn或Sn?A'Bn?A'A,B,A',B'为常数?{an}为 等比数列

等比数列的证明方法 依据定义：若an?1?q(q为常数，an?0)?{an}为等比an??an?q?q?0??n?2,且n?N*?或an?1?qan?{an}为等比数列 an?1

四、数列的通项求法：

（1）观察法：如：（1）0.2，0.22，0.222，……（2）21，203，2005，20007，……

（2）化归法：通过对递推公式的变换转化成等差数列或等比数列。

①递推式为an?1?an?d及an?1?qan（d,q为常数）：直接运用等差（比）数列。 ②递推式为an?1?an?f(n)：迭加法

如：已知{an}中a1?

11，an?1?an?，求an 24n2?13

导航教育独家经典讲义

③递推式为an?1?f(n)an：迭乘法

如：已知{an}中a1?2，an?1?n?1an，求an n

④递推式为an?1?pan?q（p,q为常数）：

构造法：Ⅰ、由??an?1?pan?q相减得(an?2?an?1)?p(an?1?an)，则

?an?2?pan?1?q

{an?1?an}为等比数列。

Ⅱ、设(an?1?t)?p(an?t)，得到pt?t?q，t?q，则p?1

{an?q} 为等比数列。 p?1

如：已知a1?1,an?1?2an?5，求an

⑤递推式为an?1?pan?qn（p,q为常数）：

两边同时除去qn?1得an?1pan1anp1b?b?，令，转化为，???b?n?1nnn?1nnqqqqqqq

再用④法解决。

如：已知{an}中，a1?511n?1，an?1?an?()，求an 632

⑥递推式为an?2?pan?1?qan（p,q为常数）：

将an?2?pan?1?qan变形为an?2?tan?1?s(an?1?tan)，可得出?出s,t，于是{an?1?tan}是公比为s的等比数列。

如：已知{an}中，a1?1,a2?2，an?2?

（3）公式法：运用an??

?s?t?p解?st??q21an?1?an，求an 33?S1,n?1?Sn?Sn?1,n?2 4

导航教育独家经典讲义

①已知Sn?3n2?5n?1，求an；②已知{an}中， Sn?3?2an，求an；

2Sn③已知{an}中，a1?1,an?(n?2)，求an 2Sn?1

（1）公式法：

①等差（比）数列前n项和公式：②1?2?3???n? ； ③212?22?32???n2?

n(n?1)2] 2n(n?1)(2n?1)6；④13?23?33???n3?[

（2）倒序相加（乘）法：

012n如：①求和：Sn?Cn； ?2Cn?3Cn???(n?1)Cn

②已知a,b为不相等的两个正数，若在a,b之间插入n个正数，使它们构成以a为首项，b为末项的等比数列，求插入的这n个正数的积Pn；

（3）错位相减法：如：求和：S?x?2x?3x???nx 23n

an?（4）裂项相消法：1?an?n(n?k)1n?k?n? 如：①S?1111?????? 1?22?33?4n?(n?1)

1111??????； 1?32?43?5n?(n?2)

1

n?n?1，则Sn?； ②S?③若an?

（5）并项法：如：求S100?1?2?3?4???99?100

（6）拆项组合法：如：在数列{an}中，an?10n?2n?1，求Sn，

六、数列问题的解题的策略：

5

导航教育独家经典讲义

（1）分类讨论问题：①在等比数列中，用前n项和公式时，要对公比q进行讨论；只有q?1

时才能用前n项和公式，q?1时S1?na1

②已知Sn求an时，要对n?1,n?2进行讨论；最后看a1满足不满足an(n?2)，若满足an中的n扩展到N*，不满足分段写成an。

（2）设项的技巧：

①对于连续偶数项的等差数列，可设为?,a?3d,a?d,a?d,a?3d,?，公差为

2d；

对于连续奇数项的等差数列，可设为?,a?2d,a?d,a,a?d,a?2d,?，公差为d； ②对于连续偶数项的等比数列，可设为?,aa,,aq,aq3,?，公比为q2； 3qq

aa2,,a,aq,aq,?公比为q； 2qq对于连续奇数项的等比数列，可设为?,

高考题

一、选择题

1.(广东卷)已知等比数列{an}的公比为正数，且a3·a9=2a5，a2=1，则a1= A. 212 B. C. 22

为等差数列，2 D.2 2（安徽卷）已知 A. -1 ，则D.7 等于 B. 1 C. 3

3.（江西卷）公差不为零的等差数列{an}的前n项和为Sn.若a4是a3与a7的等比中项, S8?32,则S10等于

A. 18 B. 24 C. 60 D. 90 4（湖南卷）设Sn是等差数列?an?的前n项和，已知a2?3，a6?11，则S7等于

A．13 B．35 C．49 D． 63 6

导航教育独家经典讲义

5.（辽宁卷）已知?an?为等差数列，且a7－2a4＝－1, a3＝0,则公差d＝

（A）－2 （B）－11 （C） （D）2 22

6.（四川卷）等差数列｛an｝的公差不为零，首项a1＝1，a2是a1和a5的等比中项，则数列的前10项之和是

A. 90 B. 100 C. 145 D. 190

27.（宁夏海南卷）等差数列?an?的前n项和为Sn，已知am?1?am?1?am?0，S2m?1?38,

则m?

（A）38 （B）20 （C）10 （D）9

8.（重庆卷）设?an?是公差不为0的等差数列，a1?2且a1,a3,a6成等比数列，则?an?的前n项和Sn=

n27nn25nn23n?? C．? A． B．443324 D．n?n 2

9.（四川卷）等差数列｛an｝的公差不为零，首项a1＝1，a2是a1和a5的等比中项，则数列的前10项之和是

A. 90 B. 100 C. 145 D. 190

二、填空题

1（浙江）设等比数列{an}的公比q?1S，前n项和为Sn，则4? 2a4

2.(山东卷)在等差数列{an}中,a3?7,a5?a2?6,则a6?____________.

3.（宁夏海南卷）等比数列{an}的公比q?0, 已知a2=1，an?2?an?1?6an，则{an}的前4项和S4=

三、解答题

1、（20xx年山东卷）已知等差数列?an?满足：a3?7，a5?a7?26，?an?的前n项和 7

导航教育独家经典讲义

为Sn

（Ⅰ）求an及Sn；（Ⅱ）令bn?

2、（2014陕西卷）已知{an}是公差不为零的等差数列，a1＝1，且a1，a3，a9成等比数列.（Ⅰ）求数列{an}的通项; （Ⅱ）求数列{2an}的前n项和Sn.

3、（2014重庆卷）

已知?an?是首项为19，公差为-2的等差数列，Sn为?an?的前n项和. （Ⅰ）求通项an及Sn；（Ⅱ）设?bn?an?是首项为1，公比为3的等比数列，求数列?bn?的通项公式及其前n项和Tn.

4、（2013北京卷）

已知|an|为等差数列，且a3??6，a6?0。

（Ⅰ）求|an|的通项公式；（Ⅱ）若等差数列|bn|满足b1??8，b2?a1?a2?a3，求|bn|的前n项和公式

5、（20xx年全国卷）设等差数列{an}的前n项和为sn，公比是正数的等比数列{bn}的前n项和为Tn，已知a1?1,b1?3,a3?b3?17,T3?S3?12,求{an},{bn}的通项公式。

6、（20xx年全国卷）

设数列?an?的前N项和为Sn,已知a2?6,6a1?a2?30,求an和Sn

7、（2011重庆卷）设(Ⅰ)求

列 1*（n?N），求数列?bn?的前n项和为Tn。 2an?1是公比为正数的等比数列，,. 的通项公式;(Ⅱ)设的前项和 8 是首项为1，公差为2的等差数列，求数

导航教育独家经典讲义

参考答案：

一、选择题

2841.【答案】B【解析】设公比为q,由已知得a1q?a1q?2a1q,即q2?2,又因为等比数??2

列{a

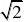
n}的公比为正数，所以q?

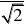
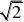
故a1?a2,选B ??q22.【解析】∵a1?a3?a5?105即3a3?105∴a3?35同理可得a4?33∴公差d?a4?a3??2∴a20?a4?(20?4)?d?1.选B。【答案】B

23.答案：C【解析】由a4?a3a7得(a1?3d)2?(a1?2d)(a1?6d)得2a1?3d?0,再由56d?32得 2a1?7d?8则d?2,a1??3,所以2

90S10?10a?d?60,.故选C 12

7(a1?a7)7(a2?a6)7(3?11)???49.故选C. 4.解: S7?222S8?8a1?

?a2?a1?d?3?a?1或由?, a7?1?6?2?13. ??1

a?a?5d?11?d?21?6

所以S7?7(a1?a7)7(1?13)??49.故选C. 22

1【答案】B 25.【解析】a7－2a4＝a3＋4d－2(a3＋d)＝2d＝－1 ? d＝－

6.【答案】B设公差为d，则(1?d)2?1?(1?4d).∵d≠0，解得d＝2，∴S10＝100

27.【答案】C【解析】因为?an?是等差数列，所以，由am?1?am?1?amam?1?am?1?2am，?0，

得：2am－am＝0，所以，am＝2，又S2m?1?38，即

－1）×2＝38，解得m＝10，故选.C。 2(2m?1)(a1?a2m?1)＝38，即（2m2

8.【答案】A解析设数列{an}的公差为d，则根据题意得(2?2d)2?2?(2?5d)，解得1n(n?1)1n27nd?或d?0（舍去），所以数列{an}的前n项和Sn?2n???? 22244

9.【答案】B设公差为d，则(1?d)?1?(1?4d).∵d≠0，解得d＝2，∴S10＝100 9 2

导航教育独家经典讲义

二、填空题

1.【命题意图】此题主要考查了数列中的等比数列的通项和求和公式，通过对数列知识点的考查充分体现了通项公式和前n项和的知识联系． a1(1?q4)s41?q4

3【解析】对于s4?,a4?a1q,??3?15 1?qa4q(1?q)

a1?2d?7??a1?32.【解析】:设等差数列{an}的公差为d,则由已知得?解得?,d?2a?4d?a?d?6?1?1

所以a6?a1?5d?13.

答案:13.【命题立意】:本题考查等差数列的通项公式以及基本计算.

q?0，3.由an?2?an?1?6an得：即q2?q?6?0，qn?1?qn?6qn?1，15

2

1(1?24)115解得：q＝2，又a2=1，所以，a1?，S4?＝。 221?2

三、解答题

1、解：（Ⅰ）设等差数列?an?的首项为a1，公差为d，

由于a3?7，a5?a7?26，所以a1?2d?7，2a1?10d?26，

解得a1?3，d?2，由于an?a1?(n?1)d，Sn?

所以an?2n?1，Sn?n(n?2)

（Ⅱ）因为an?2n?1，所以an?1?4n(n?1)因此bn?

故Tn?b1?b2???bn?2n(a1?an) ， 21111?(?) 4n(n?1)4nn?1111111(1???????) 4223nn?1

?11nn(1?)? 所以数列?bn?的前n项和Tn? 4n?14(n?1)4(n?1)

2、解 （Ⅰ）由题设知公差d≠0，

由a1＝1，a1，a3，a9成等比数列得1?2d1?8d＝， 11?2d10 解得d＝1，d＝0（舍去）， 故{an}的通项an＝1+（n－1）×1＝n.

导航教育独家经典讲义

3、

(Ⅱ)由（Ⅰ）知223am=2n，由等比数列前n项和公式得 2(1?2n)n+1Sm=2+2+2+…+2==2-2.、 1?2n

4、解：（Ⅰ）设等差数列{an}的公差d。

?a1?2d??6 因为a3??6,a6?0 所以? 解得a1??10,d?2 a?5d?0?1

所以an??10?(n?1)?2?2n?12

（Ⅱ）设等比数列{bn}的公比为q 因为b2?a1?a2?a3??24,b??8

所以?8q??24 即q=3

b1(1?qn)所以{bn}的前n项和公式为Sn??4(1?3n) 1?q

5、解设?an?的公差为d，?bn?的公比为q 由a3?b3?17得1?2d?3q?17 ① 由T3?S3?12得q?q?d?4 ②

由①②及q?0解得 q?2,d?2

故所求的通项公式为 an?2n?1,bn?3?2n?1 11 22

导航教育独家经典讲义

12

导航教育独家经典讲义

3．求数列通项公式的常用方法

（1）求差（商）法

如：数列?an?，

解 n?1时，111a1?2a2?……?nan?2n?5，求an 2221a1?2?1?5，∴a1?14 ① 2

111n?2时，a1?2a2?……?n?1an?1?2n?1?5 ② 222

①—②得：?14(n?1)1n?1a?2，∴，∴ a?2a??n?1nnnn2?2(n?2)

5an?1，a1?4，求an 3［练习］数列?an?满足Sn?Sn?1?

注意到an?1?Sn?1?Sn，代入得Sn?1?4又S1?4，∴?Sn?是等比数列，Sn?4n Sn；n?2时，an?Sn?Sn?1?……?3·4n?1

（2）叠乘法

如：数列?an?中，a1?3n?1?a

ann，求an n?1

解 3aa1a2a312n?1，∴n?又a1?3，∴an?……n?……n. a1na1a2an?123n

（3）等差型递推公式

由an?an?1?f(n)，a1?a0，求an，用迭加法 13

导航教育独家经典讲义

?

a3?a2?f(3)??n?2时，?两边相加得an?a1?f(2)?f(3)?……?f(n) …………?

an?an?1?f(n)??

∴an?a0?f(2)?f(3)?……?f(n) a2?a1?f(2)［练习］数列?an?中，a1?1，an?3

（4）等比型递推公式 n?1?an?1?n?2?，求an（an?1n?3?1?2）

an?can?1?d（c、d为常数，c?0，c?1，d?0） 可转化为等比数列，设an?x?c?an?1?x??an?can?1??c?1?x 令(c?1)x?d，∴x?ddd??a?，c为公比的等比数列 ，∴?an?是首项为?1c?1c?1c?1??

∴an?dd?n?1d?n?1d??，∴ ??a1?·ca?a?c?n??1?c?1?c?1?c?1c?1??

（5）倒数法 ，an?1?如：a1?12an，求an an?2

由已知得：a?2111111?n??，∴?? an?12an2anan?1an2∴??1?11111?1为等差数列，，公差为，∴?1?n?1·??n?1?， ???2a1an22?an?2

n?1 ∴an?

(

附：

14

公式法、利用an?? 导航教育独家经典讲义

S1n?1)

Sn?Sn?1(n?2)、累加法、累乘法.构造等差或等比

an?1?pan?q或an?1?pan?f(n)、待定系数法、对数变换法、迭代法、数学归纳法、换元法

)

4. 求数列前n项和的常用方法

(1) 裂项法

把数列各项拆成两项或多项之和，使之出现成对互为相反数的项. 如：?an?是公差为d的等差数列，求?aak?1kn1k?1 解：由111?11???????d?0? ak·ak?1akak?dd?akak?1?

n?111?11?1??11??11?1??????∴????????????……????? aadaadaaaaaak?1kk?1k?1k?1?2?3?n?1???k?2?n??1n

?1?11???? d?a1an?1?

［练习］求和：1?111??……? 1?21?2?31?2?3?……?n

1an?……?……，Sn?2? n?1

（2）错位相减法

若?an?为等差数列，?bn?为等比数列，求数列?anbn?（差比数列）前n项和，可由Sn?qSn，求Sn，其中q为?bn?的公比.

如：Sn?1?2x?3x2?4x3?……?nxn?1 ①

② x·Sn?x?2x2?3x3?4x4?……??n?1?xn?1?nxn

15

导航教育独家经典讲义

①—②?1?x?Sn?1?x?x2?……?xn?1?nxn

x?1时，Sn1?x?nx???nn

?1?x?21?x，x?1时，Sn?1?2?3?……?n?n?n?1? 2

（3）倒序相加法

把数列的各项顺序倒写，再与原来顺序的数列相加.

Sn?a1?a2?……?an?1?an??相加2Sn??a1?an???a2?an?1??…??a1?an?… Sn?an?an?1?……?a2?a1?

x2

［练习］已知f(x)?，则 21?x

?1?f(1)?f(2)?f???f(3)??2??1?f???f(4)??3?

2?1?f????4??1???x2x21x??1??由f(x)?f???????12222x1?x1?x1?x???1?1????x? ∴原式?f(1)??f(2)?f?????f(3)?f?????f(4)?f?????

??1????2????1????3????1???4??11?1?1?1?3 22

(附： a.用倒序相加法求数列的前n项和

如果一个数列{an}，与首末项等距的两项之和等于首末两项之和，可采用把正着写与倒着写的两个和式相加，就得到一个常数列的和，这一求和方法称为倒序相加法。我们在学知识时，不但要知其果，更要索其因，知识的得出过程是知识的源头，也是研究同一类知识的工具，例如：等差数列前n项和公式的推导，用的就是“倒序相加法”。 b.用公式法求数列的前n项和

对等差数列、等比数列，求前n项和Sn可直接用等差、等比数列的前n项和公式进行求解。运用公式求解的注意事项：首先要注意公式的应用范围，确定公式适用于这个数列之后，再计算。

c.用裂项相消法求数列的前n项和

裂项相消法是将数列的一项拆成两项或多项，使得前后项相抵消，留下有限项，从而 16

)

17