高等数学各部分常见的题型超强总结
以数学(一)为主总结高等数学各部分常见的题型。
一、函数、极限与连续1.求分段函数的复合函数;2.求极限或已知极限确定原式中的常数;3.讨论函数的连续性,判断间断点的类型;4.无穷小阶的比较; 5.讨论连续函数在给定区间上零点的个数,或确定方程在给定区间上有无实根。
二、一元函数微分学
1.求给定函数的导数与微分(包括高阶导数),隐函数和由参数方程所确定的函数求导,特别是分段函数和带有绝对值的函数可导性的讨论; 2.利用洛比达法则求不定式极限; 3.讨论函数极值,方程的根,证明函数不等式;
4.利用罗尔定理、拉格朗日中值定理、柯西中值定理和泰勒中值定理证明有关命题,如“证明在开区间内至少存在一点满足……”,此类问题证明经常需要构造辅助函数;
5.几何、物理、经济等方面的最大值、最小值应用问题,解这类问题,主要是确定目标函数和约束条件,判定所讨论区间; 6.利用导数研究函数性态和描绘函数图形,求曲线渐近线。
三、一元函数积分学
1.计算题:计算不定积分、定积分及广义积分;2.关于变上限积分的题:如求导、求极限等;3.有关积分中值定理和积分性质的证明题;4.定积分应用题:计算面积,旋转体体积,平面曲线弧长,旋转面面积,压力,引力,变力作功等;5.综合性试题。
四、向量代数和空间解析几何
1.计算题:求向量的数量积,向量积及混合积;2.求直线方程,平面方程;3.判定平面与直线间平行、垂直的关系,求夹角;4建立旋转面的方程;5.与多元函数微分学在几何上的应用或与线性代数相关联的题目。
五、多元函数的微分学
1.判定一个二元函数在一点是否连续,偏导数是否存在、是否可微,偏导数是否连续; 2.求多元函数(特别是含有抽象函数)的一阶、二阶偏导数,求隐函数的一阶、二阶偏导数; 3.求二元、三元函数的方向导数和梯度; 4.求曲面的切平面和法线,求空间曲线的切线与法平面,该类型题是
多元函数的微分学与前面向量代数与空间解析几何的综合题,应结合起来复习; 5.多元函数的极值或条件极值在几何、物理与经济上的应用题;求一个二元连续函数在一个有界平面区域上的最大值和最小值。这部分应用题多要用到其他领域的知识,考生在复习时要引起注意。
六、多元函数的积分学
1.二重、三重积分在各种坐标下的计算,累次积分交换次序; 2.第一型曲线积分、曲面积分计算;
3.第二型(对坐标)曲线积分的计算,格林公式、斯托克斯公式及其应用; 4.第二型(对坐标)曲面积分的计算,高斯公式及其应用; 5.梯度、散度、旋度的综合计算; 6.重积分,线面积分应用;求面积、体积、重量、重心、引力、变力作功等。数学(一)考生对这部分内容和题型要引起足够的重视。
七、无穷级数
1.判定数项级数的收敛、发散、绝对收敛、条件收敛;2.求幂级数的收敛半径、收敛域;
3.求幂级数的和函数或求数项级数的和; 4.将函数展开为幂级数(包括写出收敛域); 5.将函数展开为傅立叶级数,或已给出傅立叶级数,要确定其在某点的和(通常要用狄里克雷定理);
6.综合证明题。
八、微分方程
1.求典型类型的一阶微分方程的通解或特解:这类问题首先是判别方程类型,当然,有些方程不直接属于我们学过的类型,此时常用的方法是将x与y对调或作适当的变量代换,把原方程化为我们学过的类型;2.求解可降阶方程; 3.求线性常系数齐次和非齐次方程的特解或通解; 4.根据实际问题或给定的条件建立微分方程并求解; 5.综合题,常见的是以下内容的综合:变上限定积分,变积分域的重积分,线积分与路径无关,全微分的充要条件,偏导数等。
第二篇:高等数学微积分总结
积 分
整个高数课本,我们一共学习了不定积分,定积分,重积分(二重,三重),曲线积分(两类),曲面积分(两类).在此,我们对积分总结,比较,以期同学们对积分有一个整体的认识.
一、不定积分
不定积分是微分的逆运算,其计算方法、各种技巧是我们后面各种积分计算的基础,希望同学们熟记积分公式,及各种方法(两类换元,分部积分,有理函数积分等)
二、定积分
1.定义式: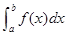
2.定义域:一维区间,例如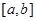
3.性质:见课本P229-P232
特殊:若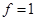 ,则
,则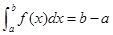 ,即区间长度.
,即区间长度.
4.积分技巧:奇偶对称性.
注意:定积分中积分变量可以任意替换即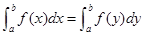 ,而不定积分不具有这种性质.
,而不定积分不具有这种性质.
5.积分方法:与不定积分的方法相同.
6.几何应用:
定积分的几何意义: 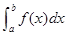 表示以
表示以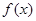 为顶与
为顶与 轴所夹区域面积的代数和(注意如
轴所夹区域面积的代数和(注意如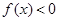 ,则面积为负);
,则面积为负);
其他应用:如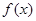 表示截面积,则积分为体积;平面弧长
表示截面积,则积分为体积;平面弧长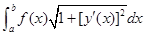 等.
等.
三、二重积分
1.定义式: 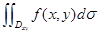
2.定义域:二维平面区域
3.性质:见下册课本P77
特殊: 若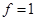 ,则
,则 ,即
,即 为
为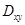 的面积.
的面积.
4.坐标系:
①直角坐标系: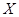 型区域,
型区域, 型区域
型区域
②极坐标系:适用范围为圆域或扇形区域,注意坐标转换后不要漏掉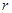 ,积分时一般先确定
,积分时一般先确定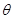 的范围,再确定
的范围,再确定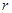 的范围.
的范围.
5.积分技巧:奇偶对称性(见后),质心;
6.几何应用:
二重积分的几何意义:若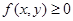 ,则
,则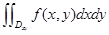 表示以
表示以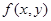 为顶以
为顶以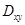 为底的曲顶柱体体积;
为底的曲顶柱体体积;
其他应用:求曲面 的面积
的面积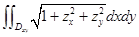
四、三重积分
1.定义式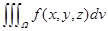
2.定义域:三维空间区域;
3.性质:与二重积分类似;
特殊: 若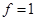 ,则
,则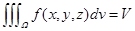 ,其中
,其中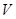 表示
表示 的体积.
的体积.
4.坐标系:
①直角坐标系:投影法,截面法(一般被积函数有一个自变量,而当该变量固定时所得截面
积易求时采用)
②柱坐标系:积分区域为柱形区域,锥形区域,抛物面所围区域时可采用;
③球坐标系:积分区域为球域或与球面相关的区域时,确定自变量范围时,先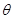 ,后
,后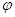 ,最后
,最后
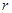 .
.
5.积分技巧:奇偶对称性,变量对称性(见后),质心等.
6.应用: 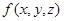 表示密度,则
表示密度,则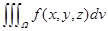 为物体质量.(不考虑几何意义)
为物体质量.(不考虑几何意义)
五、第一类曲线积分
1.定义式: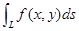 (二维)
(二维) 
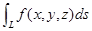 (三维)
(三维)
2.定义域:平面曲线弧  空间曲线弧
空间曲线弧
3.性质:见课本P128
特殊: 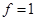 则
则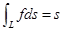 ,
,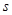 表示曲线弧长.
表示曲线弧长.
4.计算公式(二维为例):
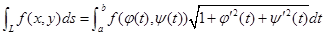
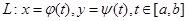
类似可推出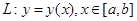 的公式.注意化为定积分时下限小于上限.
的公式.注意化为定积分时下限小于上限.
5.积分技巧:奇偶对称性,变量对称性,质心;
6.几何应用:见上3.
六、第二类曲线积分
1.定义式: 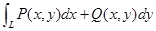 (二维)
(二维)
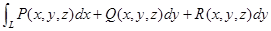 (三维)
(三维)
2.定义域:有向平面曲线弧(二维)或有向空间曲线弧(三维)
3.性质:见课本P135
4.计算公式:
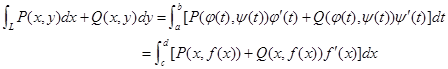
注意:曲线积分化为定积分时,下限为起始点,上限为终点.
5.积分技巧:二维曲线积分可以应用格林公式(注意使用条件).积分与路径无关.
不能使用奇偶对称性.
6.应用:力做功.
七、第一类曲面积分
1.定义式: 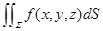
2.定义域:空间曲面
注意:空间曲面与坐标面重合或平行时,即为二重积分,故二重积分时第一类曲面积分的特例.
3.性质:见课本:与第一类曲线积分类似
特殊: 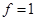 则
则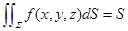 ,
, 表示曲线面积.
表示曲线面积.
4.计算公式: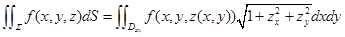 类似可得在另两个曲面上的投影公式.
类似可得在另两个曲面上的投影公式.
注意对于特殊的曲面如柱面考虑使用柱坐标,曲面考虑使用球坐标.
5.积分技巧:奇偶对称性,变量对称性,质心.
6.几何应用:见上3.
八、第二类曲面积分
1.定义式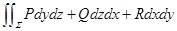
2.定义域:有向空间曲面
3.性质:见课本P162
4.计算公式: 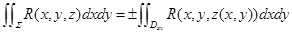 ,类似可得另两个.
,类似可得另两个.
5.积分技巧:高斯公式,循环对称性.不能使用奇偶对称性.
注:要熟练掌握使用高斯公式做第二类曲面积分的题目,使用时要注意曲面方向以及是否封
闭.
6.应用:求流量,磁通量等.
奇偶对称性:
定积分:若积分区间关于原点对称,例如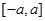
若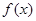 关于
关于 为奇函数,则
为奇函数,则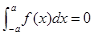
若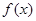 关于
关于 为偶函数,则
为偶函数,则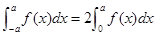
二重积分:若积分区域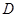 关于
关于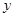 轴对称,记
轴对称,记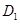 为
为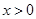 的部分
的部分
若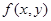 关于
关于 为奇函数,则
为奇函数,则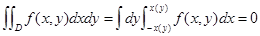
若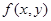 关于
关于 为偶函数,则
为偶函数,则
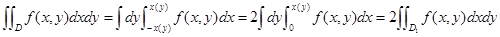
同样可以得到积分区域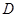 关于
关于 轴对称时,
轴对称时, 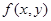 关于
关于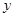 为奇、偶函数的公式.
为奇、偶函数的公式.
三重积分: 若积分区域 关于
关于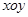 面对称,记
面对称,记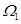 为
为 的部分
的部分
若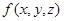 关于
关于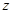 为奇函数,则
为奇函数,则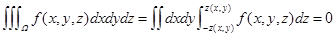
若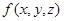 关于
关于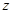 为偶函数,则
为偶函数,则
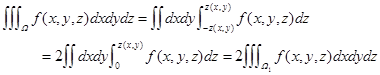
同样可以得到区域关于另两个曲面对称的情况.
例题:P123#1(1)(2) P124#2(4)
第一类曲线积分:若积分曲线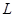 关于
关于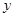 轴对称,记
轴对称,记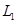 为
为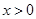 的部分
的部分
若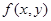 关于
关于 为奇函数:
为奇函数: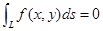
若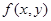 关于
关于 为偶函数:
为偶函数: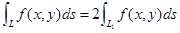
同样可以得到曲线关于 轴对称的情况.
轴对称的情况.
第一类曲面积分:若积分曲面 关于
关于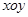 面对称,记
面对称,记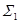 为
为 的部分,
的部分,
若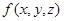 关于
关于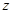 为奇函数:
为奇函数: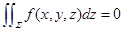
若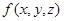 关于
关于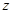 为偶函数:
为偶函数: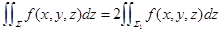
同样可以得到曲面关于另两个坐标面对称的情况.
例题:课本P158#6(3),P184#2
变量对称性:一般在做重积分、曲面积分时使用,
使用时要注意曲面或区域必须是关于变量是对称的,即对于曲面方程自变量相互替换后方程不改变,例如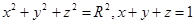 等,此时
等,此时
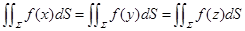
例题1: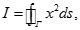 其中
其中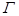 为球面
为球面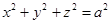 被平面
被平面 所截的曲线.
所截的曲线.
例题2: 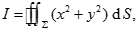 其中
其中 为球面
为球面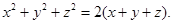
循环对称性(适用第二类曲面积分):若积分曲面满足变量对称,而且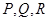 中
中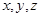 依次替换,即
依次替换,即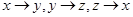 后积分表达式不改变,则可以使用该对称性,有
后积分表达式不改变,则可以使用该对称性,有
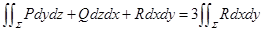
例题:课本168页#3(4)
质心:适用重积分,第一类积分.
请同学们思考如何区别各种积分?(定义域)
区别:以下两个例题应该怎样算?
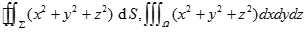 ,
,
其中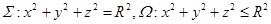
-
高数:总结求极限的常用方法
总结求极限的常用方法,详细列举,至少4种极限定义法泰勒展开法。洛必达法则。等价无穷小和等价无穷大。极限的求法1.直接代入法适用于分…
-
同济六版上册高数总结(一些重要公式及知识点)
同济六版上册高数总结微分公式与积分公式(tgx)??secx(ctgx)???csc2x(secx)??secx?tgx(cscx…
-
高数总结
高数重点知识总结1、基本初等函数:反函数(y=arctanx),对数函数(y=lnx),幂函数(y=x),指数函数(),三角函数(…
-
考研数学解题技巧高数总结,删除广告word版
函数极限:数列的极限(特殊)——函数的极限(一般)极限的本质是通过已知某一个量(自变量)的变化趋势,去研究和探索另外一个量(因变量…
-
考研.数学 高数总结3
定积分理论一、实际应用背景1、运动问题—设物体运动速度为v?v(t),求t?[a,b]上物体走过的路程。(1)取a?t0?t1??…
-
大一高数(下)2,大一下学期高数总结归纳
高等数学下期末考试2一填空题共12分13分若a132b514则ab23分曲面x2y2z214在点123处的法线方程为33分微分方程…
-
大一高数(下)2,大一下学期高数总结归纳
河北科技大学高等数学下期末考试2一填空题共12分13分若a132b514则ab23分曲面x2y2z214在点123处的法线方程为3…
-
Bogepju高数考研经验总结和考试重点罗列
七夕古今诗人惯咏星月与悲情吾生虽晚世态炎凉却已看透矣情也成空且作挥手袖底风罢是夜窗外风雨如晦吾独坐陋室听一曲尘缘合成诗韵一首觉放诸…
-
Kcmfbr高数考研经验总结和考试重点罗列
秋风清秋月明落叶聚还散寒鸦栖复惊总结高分经验我认为有以下几点要引起注意一一定要夯实基础不放过书上的每一道题书中例题自己要先试着做一…
-
zbtfie考研数学总结高数篇
懒惰是很奇怪的东西它使你以为那是安逸是休息是福气但实际上它所给你的是无聊是倦怠是消沉它剥夺你对前途的希望割断你和别人之间的友情使你…