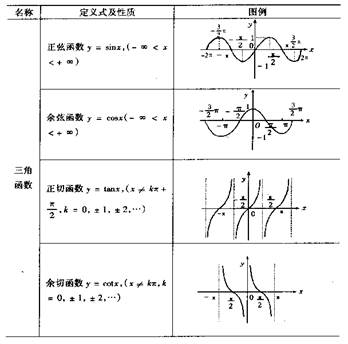
篇一 :高等数学-上册-第一章总结
第一章 函数极限与连续
(一) 本章重点(important points):
1. 了解极限的定义(重点是理解极限定义中的“任意”和“存在”,以及N与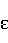 的相关性;动态变化性)及求法,定义要从代数及几何两方面进行理解。
的相关性;动态变化性)及求法,定义要从代数及几何两方面进行理解。
2. 理解以及运用两个重要的极限公式(及其拓展形式)。
3. 无穷小理论及其运用(主要是等价无穷小代换,在求极限以及一些证明题中会经常用到,so it is also important!)。
4. 函数的连续(这是以后很多公式定理运用的条件,所以必须掌握地very good!)。
5. 分段函数的连续性,可导性,及其极限值的求法。
(二) 知识点分析(analysis):
…… …… 余下全文
篇三 :大一高数第一章复习总结及相关习题
第一章 函数与极限习题课
一、主要内容
(一)函数的定义
(二)极限的概念
(三)连续的概念
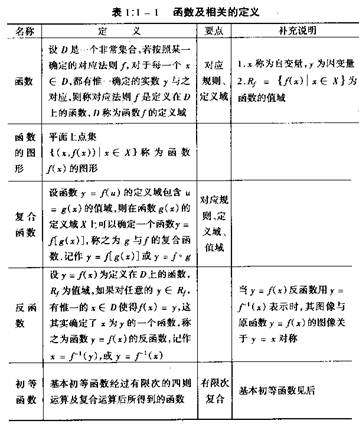
一)函数
1.函数的定义 函数的分类
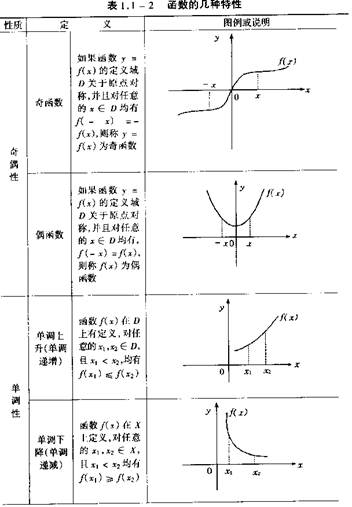
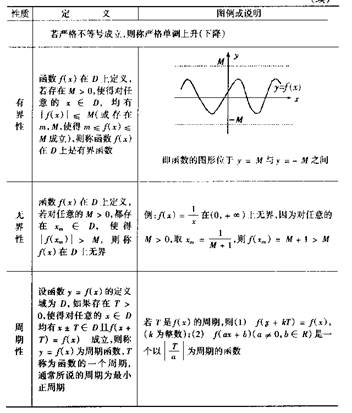
2.函数的性质 有界、单调、奇偶、周期
3.反函数
4.隐函数
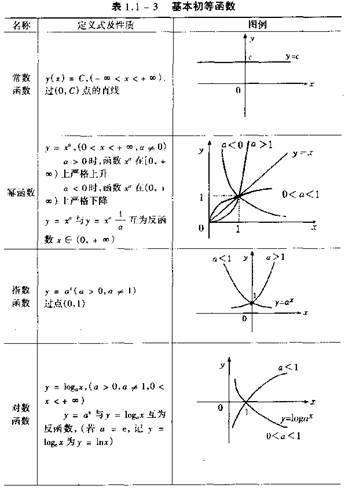
5.基本初等函数
6.复合函数
7.初等函数
8.双曲函数与反双曲函数
(二)极限
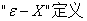
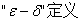
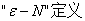 1、极限的定义:
1、极限的定义:
单侧极限 极限存在的条件
2、无穷小与无穷大
无穷小; 无穷大; 无穷小与无穷大的关系 无穷小的运算性质
3、极限的性质 四则运算、复合函数的极限
4、求极限的常用方法
a.多项式与分式函数代入法求极限;
b.消去零因子法求极限;
c.无穷小因子分出法求极限;
d.利用无穷小运算性质求极限;
e.利用左右极限求分段函数极限;
f.利用等价无穷小;
g.利用重要极限
5、判定极限存在的准则 夹逼定理、单调有界原理
…… …… 余下全文
篇四 :高等数学第一章总结
高等数学
多元函数微分法
及其应用学习总结
一.知识结构图
多元函数微分学:
l 基本概念(区域.定义.极限.连续)
l 偏导数(定义.计算.高阶偏导数)
l 全微分(定义.计算.必要条件.充分条件)
l 多元复合函数导数(链式法则.全导数)
l 隐函数求导法则(一个方程.方程组)
l 多元函数微分学的几何应用(曲线以及曲面的切线和法平面)
l 方向导数及其梯度
l 多元函数最值及其求法
二.内容提要
1) 二次极限定义:
设f(x,y)的区域D内有定义,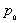 (
(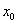 ,
,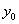 )是D的聚点,若
)是D的聚点,若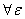 >0,
>0,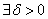 ,当点P(x,y)满足
,当点P(x,y)满足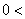 |
|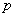
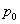 |<
|<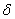 时,总有
时,总有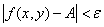 成立,则称函数
成立,则称函数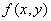 当(x,y)趋向
当(x,y)趋向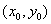 时以A为极限,记作
时以A为极限,记作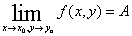 或
或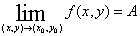 .
.
2) 二元函数连续性定义
设函数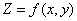 在点
在点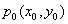 的某个邻域
的某个邻域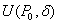 内有定义,若
内有定义,若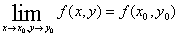 ,则称二元函数
,则称二元函数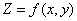 在点
在点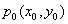 处连续,点
处连续,点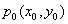 称为
称为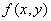 的连续点。
的连续点。
…… …… 余下全文
篇五 :考研数学之高等数学讲义第一章(考点知识点+概念定理总结)
高等数学讲义
目 录
第一章 函数、极限、连续·················································· 1
第二章 一元函数微分学····················································· 24
…… …… 余下全文
篇六 :高数 第1章 极限计算方法总结
极限计算方法总结
一、极限定义、运算法则和一些结果
1.定义:
数列极限、函数极限,课本42页的表格必须认真填写并掌握。
说明:(1)一些最简单的数列或函数的极限(极限值可以观察得到)都可以用上面的极限严格定义证明,例如: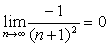 ;
; ;
;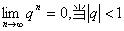 等。
等。
定义证明按着总结的四个步骤来,缺一不可!(2)在后面求极限时,(1)中提到的简单极限作为已知结果直接运用,而不需再用极限严格定义证明。
2.极限运算法则
定理1 已知 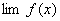 ,
,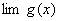 都存在,极限值分别为A,B,则下面极限都存在,
都存在,极限值分别为A,B,则下面极限都存在,
且(1)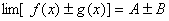 (2)
(2)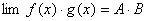
(3)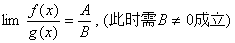 说明:极限号下面的极限过程是一致的;同时注意法则成立的条件,当条件不满足时,不能用。
说明:极限号下面的极限过程是一致的;同时注意法则成立的条件,当条件不满足时,不能用。
3.两个重要极限
(1) 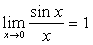 (2)
(2)  ;
; 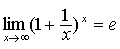
说明:(1)不仅要能够运用这两个重要极限本身,还应能够熟练运用它们的变形形式。
(2)一定注意两个重要极限成立的条件。
例如: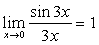 ,
,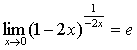 ,
, ;等等。
;等等。
4.等价无穷小
定理2 无穷小与有界函数的乘积仍然是无穷小(即极限是0)。
定理3 当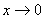 时,下列函数都是无穷小(即极限是0),且相互等价,即有:
时,下列函数都是无穷小(即极限是0),且相互等价,即有:
…… …… 余下全文
篇七 :插本高数第一章 易忘点总结(函数、极限与连续)
第一节 函数
一、求表达式;
(1)已知函数f[g(x)]的表达式,求函数f(x)的表达式。 解:①令u=g(x),从中反解出x=φ(u),再求出f(u)的表达式,然后将u换为x,可得f(x);
②将函数f[g(x)]的表达式凑出g(x)的函数关系式,然后将所有g(x)的位置换为x,即得f(x);
自我理解:本人觉得第一种是通用的;第一种运用的是反推,也就是反代转换的意思,相当于原本是乘以了“一个数”,然后反过来解时再除以“这个数”的意思!
(2)已知函数f(x)和f[g(x)]的表达式,求函数g(x) 自我总结:将g(x)代入f(x)得出表达式= f[g(x)]的表达式,得出g(x)
二、函数的简单性质;
1、单调性 2、奇偶性 3、周期性 4、有界性
(1)单调性判定:
①定义判定: x2>x1 , f x2 ?f x1 >0 , 则增
x?f x
2>x1 , f x21 <0 ,则减
②导数判定: f′ x >0 增
f′ x <0 减
第一章 易忘点总结(函数、极限与连续)
…… …… 余下全文
篇八 :考研.数学 高等数学总结1
中值定理及应用
一、基本概念定理
1、极值点与极值—设连续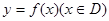 ,其中
,其中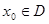 。若存在
。若存在 ,当
,当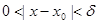 时,有
时,有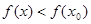 ,称
,称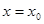 为
为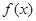 的极大点;若存在
的极大点;若存在 ,当
,当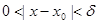 时,有
时,有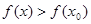 ,称
,称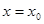 为
为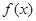 的极小点,极大点和极小点称为极值点。
的极小点,极大点和极小点称为极值点。
2、极限的保号性定理
定理 设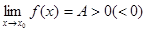 ,则存在
,则存在 ,当
,当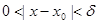 时,
时,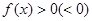 ,即函数极限大于零则邻域大于零;极限小于零则邻域小于零。
,即函数极限大于零则邻域大于零;极限小于零则邻域小于零。
【证明】设 ,取
,取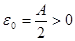 ,因为
,因为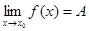 ,由极限的定义,存在
,由极限的定义,存在 ,当
,当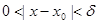 时,
时,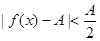 ,于是
,于是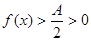 。
。
3、极限保号性的应用
【例题1】设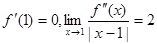 ,讨论
,讨论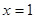 是否是极值点。
是否是极值点。
【例题2】(1)设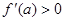 ,讨论
,讨论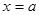 是否是
是否是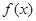 的极值点;
的极值点;
(2)设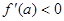 ,讨论
,讨论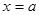 是否是
是否是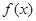 的极值点。
的极值点。
【解答】(1)设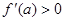 ,即
,即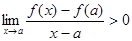 ,由极限的保号性,存在
,由极限的保号性,存在 ,当
,当 时,有
时,有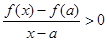 。
。
当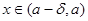 时,
时,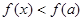 ;当
;当 时,
时,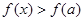 。
。
显然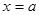 不是
不是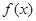 的极值点。
的极值点。
(2)设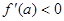 ,即
,即 ,由极限的保号性,存在
,由极限的保号性,存在 ,当
,当 时,有
时,有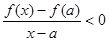 。
。
当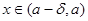 时,
时,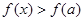 ;当
;当 时,
时,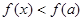 。
。
显然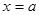 不是
不是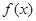 的极值点。
的极值点。
【结论1】设连续函数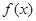 在
在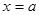 处取极值,则
处取极值,则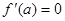 或
或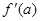 不存在。
不存在。
【结论2】设可导函数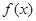 在
在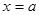 处取极值,则
处取极值,则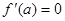 。
。
二、一阶中值定理
定理1(罗尔中值定理)设函数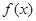 满足:(1)
满足:(1)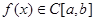 ;(2)
;(2)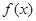 在
在 内可导;(3)
内可导;(3)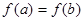 ,则存在
,则存在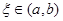 ,使得
,使得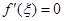 。
。
定理2(Lagrange中值定理)设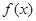 满足:(1)
满足:(1)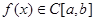 ;(2)
;(2)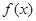 在
在 内可导,则存在
内可导,则存在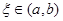 ,使得
,使得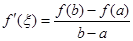 。
。
【注解】
(1)中值定理的等价形式为:
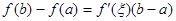 ,其中
,其中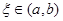 ;
;
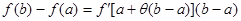 ,其中
,其中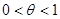 。
。
…… …… 余下全文